一类单调数列极限的求法

万为国

（长江大学 一年级教学工作部，湖北 荆州 434001）

数列极限的计算方法中，单调有界原理是一种非常有效的方法.有些数列的极限，用其它方法不一定能求出极限值，用单调有界原理却能迎刃而解.应用单调有界原理求极限时，许多情况下，往往是证明数列单调增加有上界，或者单调减少有下界，由此确定数列有极限.

定理 单调有界数列必有极限.这个定理就是单调有界原理（证明略）［1］50－55.

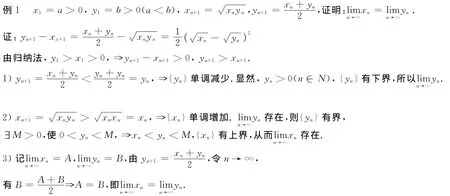
还有一类数列，求它的极限要用到单调有界原理，却不清楚它是单调增加还是单调减少的.这类数列极限的求法，可以考虑一种新的思路，先证明它是单调的，不用知道其增减性，再证明数列有界，确定极限存在并求值.

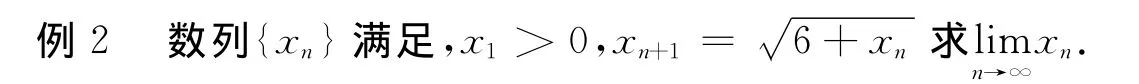
这个数列｛xn｝，既有可能单调增加，也有可能单调减少，不妨换一种思路求解.

从而0＜xn＜ max｛x1，x2，x2＋｜x2－x1｜｝，（n∈N），｛xn｝有界，

类似于例2、例3这种类型的数列，采用例2、例3这种解法，有益于拓宽思路，有时也能简化解题过程.

［1］同济大学数学系.高等数学（上册）［M］.北京：高等教育出版社，2007.

［2］复旦大学数学系.数学分析（上册）［M］.北京：高等教育出版社，2002.