基于图嵌入的特征提取算法研究
2013-10-24王化喆
王化喆,刘 佳,,王 胜
(1.商丘职业技术学院,河南 商丘 476000;2.南京理工大学,江苏 南京 210000)
1 图的定义
一个图G就是一个有序的三元组(V(G),E(G),ΨG),其中V(G)是非空的顶点集,内部元素称为图G的顶点,E(G)是不相交的边集,内部的元素称为图G的边.ΨG称为关联函数,它使G的每条边对应于G的无序顶点对.如图1所示:
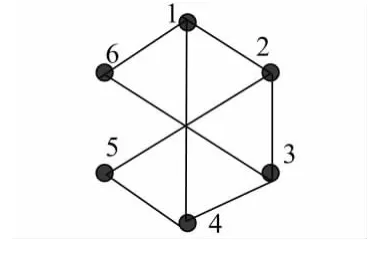
图1 图G的结构
2 图嵌入
G={X,W}是一个图,其中X为顶点集,W 为相似度矩阵,W ∈RN×N.Wij度量数据点Xi与Xj的相似度,如果Wij=0就认为点xi,xj的相似度为0.W 可以依据不同的准则来定义.图G的对角矩阵D和拉普拉斯(Laplacian)矩阵L定义如下:

该文的图嵌入定义如下:
设向量x∈RD,y∈Rd,(d≪D),x→y,并且数据集Y能够很好地保持原来数据集X相似关系(即图G).假设数据集X的本质图为G,惩罚图为Gp.图结构保持准则定义如下:
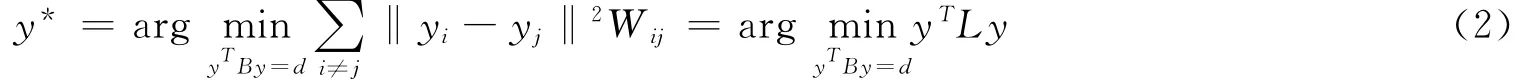
其中L定义如公式(1),限制条件yTBy=d用来获得最优的数据.
B的定义如下:若只有本质图时B=D,此时B作为一个图归一化矩阵;当有惩罚图时B=LP=DPWP,DP定义如公式(2),此时B作为一个惩罚项.图结构保持含义如下:原始数据相似度较小的点相似度变小,原始数据相似度较高的点映射之后相似度变大.
由于上述图结构保持准则只计算出训练样本的低维嵌入,而不是全体样本的.因此,下面介绍一种线性化的嵌入映射[1]2323-2325.
设向量x∈RD,y∈Rd,(d≪D),x→y=,P为映射变换向量。此时公式(2)可变化为下式:
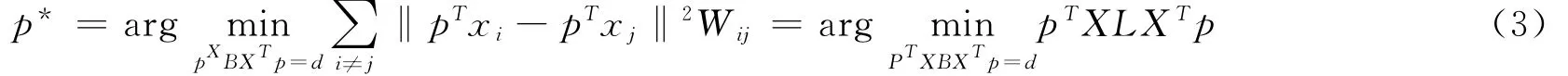
归一化后的映射变换向量P,即为映射变换的方向。可以通过核化来计算非线性映射变换向量,通过张量化来计算映射变换矩阵.
3 基于图嵌入的算法分析
3.1 主成分分析
主成分分析(Principal Components Analysis,PCA),本质上是数学统计的特征分析算法,基于PCA算法抽取出的人脸特征——特征脸.基于特征脸的人脸识别算法是较为经典的识别算法之一,成为鉴别新算法优劣的基准算法之一[2]40.其基本原理如下:
设样本数据集X = (x1,x2,…,xN),其中xi∈RD,i=1,2,…,N.样本xi的类别标签为ci∈ {1,2,…,Nc},其中Nc为样本数据集类别数,第i类的样本的总数为ni.PCA寻找最优的映射变换矩阵P,将iD空间的数据映射到一个相对低维的特征空间id((d≪D))中.
样本数据集的平均值为:

则其协方差矩阵如下:

其目标函数为:
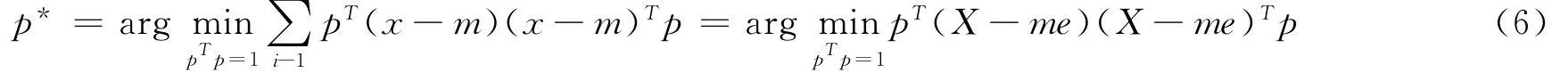
协方差矩阵可以推导如下:

3.2 线性鉴别分析
线性鉴别分析(LDA)的主要思想是:计算使得Fisher准则函数得到最大值的向量作为映射向量.即使类间散度矩阵和类内散度矩阵之商获得最大值的向量,因此该向量可以通过计算类间散度矩阵和类内散度矩阵的广义特征向量获得.
最佳鉴别矢量投影矩阵的计算,利用矩阵论相关知识使该投影矩阵投影后保证有最大类间距和最小类内距,即具有最大的可分离性[3]67.因此,它是一种有效的特征抽取方法.其基本原理如下:
设样本数据集X = (x1,x2,…,xN),其中xi∈RD,i=1,2,…,N.样本xi的类别标签为ci∈ {1,2,…,Nc},其中Nc为样本数据集类别数,第i类的样本的总数为ni.LDA寻找最优的映射变换矩阵P,将iD空间的数据映射到一个相对低维的特征空间id(d≪D)中[4]100.令映射函数为:

i类样本均值计算如下:

总体样本均值:

根据类间离散度矩阵和类内离散度矩阵定义,可以得到如下式子:
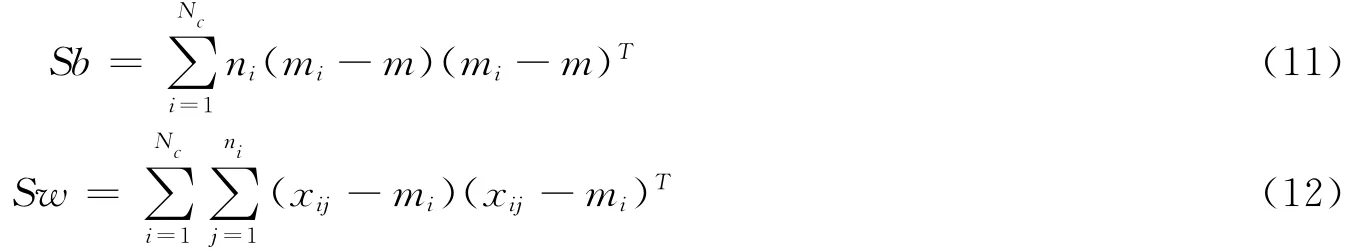
与LDA类似,MFA的目标函数如下:

类间离散度矩阵可以变换为:

类内离散度矩阵可以变换为:

故LDA的目标函数可以变换为:
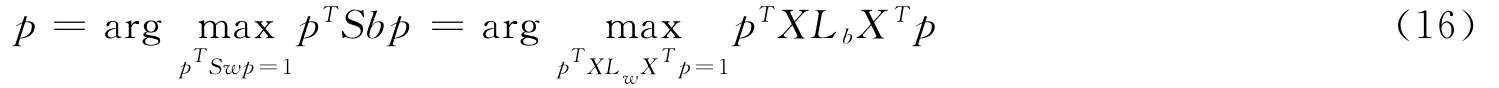
由公式(16)可以看出LDA也可以看做一种图嵌入.
3.3 L1图及其嵌入
设数据集X= (x1,x2,…,xN),其中xi∈RD,i=1,2,…,N..L1图的目的是利用训练样本表示每一个训练样本,同时要求用来表示每一个测试样本的训练样本尽可能的稀疏.
L1计算方法如下:
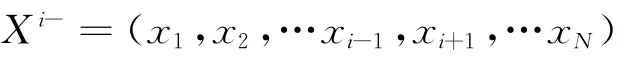
其中ai∈RN-1;
利用NPE类似的方法可以实现L1图的嵌入。同时,嵌入映射变换矩阵P可以通过计算下面最小化问题得到:

约束条件为PTXXTP=1.其中tr表示矩阵的迹,M的定义如下:

4 结论
通过对PCA,LDA,L1等经典算法的代数推导及对比可以得出,这些经典算法都可以利用图嵌入框架理论来解释并统一到此种框架中.由此,得出特征提取算法的核心是样本的图构造,对于降低特征提取算法的计算复杂度和提高算法的效率有较好的效果[5]189-201.
[1]T.Roweis,L.K.Saul.Nonlinear Dimensionality Reduction by Loeally Linear Embedding[J].Seienee,2000,290(5500).
[2]C.Yan,D.Xu,B.Y.Zhang.Graph embedding andextensions:ageneral framework for dimensional-ity reduetion.IEEE Tran[J].s.on Pattern Analysis and Maehine Intelligenc,2007,29(1).
[3]黄 鸿.图嵌入框架下流形学习理论及应用研究[D].重庆:重庆大学,2008.
[4]边肇棋,张学工.模式识别(第二版)[M].北京:清华大学出版社,2000.
[5]X.F.He,D.Cai.Learning a Maximum Margin SubsPa-ce for Image Retrieval[J].IEEE Trans.on Knowledge and Data Engineering,2008,20(2).
