基于Petri 网的软件故障树分析
2013-10-21杨瀚程
林 红 杨瀚程
(电子科技大学 成都 611731)
0 引言
软件可靠性分析是保证软件可靠性的重要步骤,是软件可靠性工程一个重要的阶段。其中,软件故障树分析[1]方法有着巨大的工程适用性和强大的生命力。故障树可看做系统中故障的传播关系,通过图形表示和数学描述,通过演绎方式找出导致系统故障原因,求出系统薄弱环节,指导可靠性指标分配和可靠性设计。故障树不仅能定性分析软件系统可靠性,还能定量分析软件系统可靠性。故障树的分析方法主要有上行法和下行法。但对于大型复杂的故障树采用上行和下行的方法显得太过繁琐。
Petri 网是C.A.Petri 于1962 年在他的博士论文中首次提出的[2]。Petri 网能够刻画系统的结构,且描述系统的动态行为,有直观的图形表示,同时能够引入多种数学方法进行分析。经过几十年的发展,Petri 网理论已经非常成熟,并且在计算机科学技术、自动化科学技术、机械设计与制造以及其他科学领域得到广泛的应用。Petri 网具有丰富的图形化和数学化分析方法,主要有可达标识图与可覆盖树,关联矩阵与状态方程,Petri 网语言和Petri 网进程,这些方法都建立在坚实的数学基础上,各有其使用方式。本文提出了通过Petri 网关联矩阵法求解软件系统故障树最小割集的算法,并通过我院研制的ADS-B 系统中最重要的工作信息解码分析进行了验证。
1 软件故障树的Petri 网模型
故障树以图的形式表示事件之间的逻辑关系,它由规定的事件,逻辑门和其他符号描述系统中事件的因果关系[3]。逻辑门的输入为因,输出为果。位于故障树最底层事件为底事件,位于故障树顶端事件为顶事件,中间事件是除顶事件和底事件以外的事件。使用逻辑门,如与门、或门、表决门,非门等描述事件的因果关系。故障树首先确定一个软件中的故障,然后在一定环境和条件下分析软件,找出不希望发生事件发生的确切方式,即原因。寻找导致系统故障的全部故障模式是故障树分析的主要任务。故障模式即系统的薄弱环节,也即系统的割集,加强薄弱环节的设计可以提高软件可靠性。如果割集中任一底事件不发生则顶事件不发生,这样的割集称为最小割集。求解最小割集对降低复杂系统潜在事故的风险具有重大的意义。
与一般系统模型类似,Petri 网有两类元素构成:表状态的元素和表变迁的元素。Petri 网采用S-元代表状态元素,T-元代表变迁元素[5]。S-元和T-元同等对待,是分体的,两者相互依赖。T-元引起S-元资源的流动,流关系用于联系这两者之间的关系,用F 表示。Petri 网的系统行为表现为资源的流动。在图形表示中,用小圆圈表示一个S-元,用小矩形表示一个T-元,用有向边表示S-元和T-元的关系。Petri 网具有可达性、有界性、安全性,可覆盖性、可逆性以及守恒性等特性。这些优良的数学特性可以较好的描述复杂系统中常见的同步、并发、分布、冲突、资源共享等现象,同时有着丰富的分析方法。其中,关关联矩阵分析法适合用于大规模的复杂性较高的Petri 网模型。关联矩阵法充分利用线性代数方式解决网的分析,并易于使用计算机仿真分析。
对于软件的故障树模型,很容易转化为Petri网[4]。故障树的与门采用一个变迁代替,或门采用相应的多个变迁表示。对应关系如图1 所示。然后使用Petri 网分析方法分析Petri 的状态,由相应关系求解故障树的参数,例如最小割集[5]。故障树中通常出现重复事件,可使用Petri 网建模方式合并相同事件,缩小模型规模。
2 使用Petri 网关联矩阵求解故障树最小割集算法
算法具体步骤如下:
A.画出软件系统各事件间的逻辑关系,构成故障树。分析软件系统中最重要的故障,作为顶事件,逐层细化分析造成顶事件的原因。

图1 故障树表示与Petri 网表示对应关系
B.求出故障树对应的Petri 网。对已形成的故障树,与门采用一个变迁表示,或门采用多个变迁表示,事件用库所表示,添加流关系,形成Petri 网。对故障树的重复事件,Petri 网中使用一个库所表示。
C.求解关联矩阵。文献[2]详细描述了求解关联矩阵的算法,这里不再赘述。
D.由关联矩阵求解系统最小割集,步骤如下:
a.找出关联矩阵中只有“1”和“0”,没有“-1”的行,则此行代表的库所只有输入库所,没有输出库所,则此行为对应事件顶库所。
b.按次序寻找顶库所对应行的“1”,并按列寻找到“-1”,此“-1”代表此行对应事件为顶库所一个输入事件,若有多个“-1”,说明同一变迁有多个输入库所,为“与”关系。
c.由(b)中找到的“-1”按行寻找“1”,若存在“1”说明是中间库所。继续按(b)的步骤循环查找,直到所在行没有“1”为止。所在行没有“1”,代表该行对应库所为底库所。若此行有多个“1”,说明对应的库所对应多个变迁,为“或”关系。
d.按步骤(b)、步骤(c)继续查找,直到查找到最底层库所。
e.按照上面的“与”“或”关系,将底库所展开,得到所有割集。
f.采用几何化简方法化简割集,得到最小割集。
3 算法实例——ADS-B 解码任务故障树分析
我院研制的ADS-B 地面系统实现了ADS-B消息的接收与解码,并将解码后的消息送入主控。其中ADS-B 消息的解码是本系统的核心单元。下面将使用这个任务验证本文的算法,解码采用协议为RTCA DO-260A。
该任务的主要功能为由特定的时间条件,或中断条件接受FPGA 从外部接收的数据,对接收按飞行器分类处理,再对消息按消息类型分类,判断是否是经纬度消息,速度消息等,按照一定的解码协议解码,解码后由一定的条件发送出去。
由系统分析,故障树形式[7]如图2 所示。根据以上算法,求出对应的Petri 网如图3 所示。求出关联矩阵如公式(1)所示。


图2 解码ADS-B 消息故障树表示

图3 对应的Petri 网表示
以下由关联矩阵求故障树最小割集:
a.搜索只有“1”和“0”没有“-1”的行,此例中为17 行,得

b.对行16,15,14 分别找为1 的列,重复上述步骤,得到

c.重复上述步骤,依次向下分解,得到

将所有底库所求出后,将以上算式逐级带入,并整理后得:
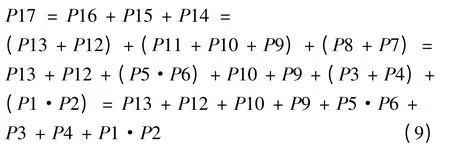
因此,求出故障树的最小割集为{P13},{P12},{P10},{P9},{P6,P5},{P3},{P4},{P2,P1}。
通过以上实例可以看到,基于Petri 网关联矩阵法能够有效求解故障树最小割集,算法清晰,易于计算机实现。同时适用于大型且结构比较复杂的系统。
4 结束语
故障树转换为Petri 网能够有效的缩小软件故障树规模。故障树与Petri 网的结合有效的利用了故障树描述系统故障的能力以及Petri 网丰富的化简和分析方法。文中使用Petri 网的关联矩阵法求解故障树的最小割集能够较好应对大型复杂的系统,算法易实现。
[1]孙志安,裴晓黎,宋昕.软件可靠性工程[M].北京:北京航空航天大学出版社,2009.
[2]吴哲辉.Petri 网导论[M].北京:机械工业出版社,2006.
[3]程鹏,隽吉昌,龚洁.基于故障树的软件分析技术(SFTA) 浅析[J].中国新技术新产品,2009,21:35.
[4]秦兴秋,邢昌风.一种基于Petri 网模型求解故障树最小割集的算法[J].计算机应用,2004,6,24:209-306.
[5]严传龙.组合导航系统软件可靠性分析与研究[D].哈尔滨:哈尔滨工程大学,2008.
