临近空间目标运动建模与跟踪方法研究
2013-10-21张远吴昊
张 远 吴 昊
(中国电子科技集团公司第38 研究所 合肥 230088)
0 引言
临近空间高超声速目标能够在稀薄大气层做持续的高超声速运动,具有飞行速度快、机动能力强、投送能力远、突防能力强的特点,将成为未来重点发展的武器装备。目前由于探测手段和实际数据的缺乏,高超声速目标是跟踪领域新兴的一类目标,没有经过应用证明的实用跟踪方法,对于它的研究还处于不成熟阶段[1,3]。临近空间目标探测雷达是我国下一步重点发展的探测装备,因此研究高效的临近空间目标跟踪方法,提高该类目标的跟踪性能,是雷达目标跟踪领域的迫切需求。本文对临近空间高超声速飞行器的飞行特性进行分析,根据其动力学模型,建立临近空间高超声速飞行器的运动模型,采用交互多模型滤波(IMM)方法进行跟踪。采用Monte-Carlo 仿真实验,本文提出的目标运动模型和跟踪算法对临近空间高超声速目标的跟踪性能有明显改善。
1 临近空间目标的飞行特性
本文研究的高超声速飞行器在30 km~60 km的临近空间进行跳跃飞行,其飞行轨道如图1 所示。

图1 跳跃飞行轨迹
高超声速飞行器在进入临近空间后,一般采用跳跃飞行轨道,运动轨道简化为3 个阶段:助推段、巡航段和攻击段。由于临近空间高超声速飞行器所特有的这种飞行特性,它能够在很短的时间内完成加速,往往在巡航段开始几百秒的时间内速度就可达到6~7 Ma。以X-51 为例,它由一架轰炸机携带飞至15.24 km 的高空后释放,助推级点火工作约30 s,将飞行器推至18.29 km 的高空并达4.5 Ma;在助推级燃料燃尽后,助推级与中间级和巡航级分离,中间级分离后,巡航级在无动力状态下滑翔数秒后,超然冲压发动机开始进入高超声速试验阶段,巡航级的发动机点火后工作300 s,使飞行器爬升到大约24 km 的高度,且速度达到7 Ma;发动机熄火后,飞行器在500 s 的下降阶段内进行机动飞行[3],并按此规律循环运动。
2 临近空间目标运动模型
临近空间高超声速飞行器航程远,建模时不能按飞机建模一样把地面视为平面,但地球自转等因素对运动过程的影响较小,一般可作如下假设:
a.地球是一个均匀球体,不考虑地球扁率,地球公转及地球自转;
b.大气相对地球是静止的且同一高度上均匀,忽略大气参数的摄动;
c.飞行器为无动力返回的质点;
d.再入飞行器的侧滑角为零。
基于以上考虑,在地心惯性坐标系中,临近空间目标飞行器的动力学方程如下[1-2]:


其中:h 为高度;M 为马赫数;γ 为航迹倾角;χ 为航迹方位角;λ 为经度;φc为纬度;c 为声速;φv为速度滚转角;R 为地球半径;P 为推力;α 为迎角;D 为阻力;L 为升力;m 为飞行器质量;g 为重力加速度;Isp为比冲。
阻力D 与阻力系数CD,机翼面积S,大气密度ρ和飞行器速度v(即Mc)有关,具体表达式为:

升力L 与升力系数CL,机翼面积S,大气密度ρ和飞行器速度v 有关,具体表达式为:

重力加速度g 表示为:

其中地球引力常数μ=3.986004418 ×1014。大气密度的标准分布取为指数规律

其中R*为以重力工程制单位表示的海平面干燥空气之气体常数,其值为R*=29.27kg·m/kg·℃,T0为海平面的绝对温度,取为T0=288.15K,ρ0为海平面大气密度,取为ρ0=1.2250kg/m3。
3 临近空间目标跟踪算法
从式(1)~(12)可以看出,临近空间目标的运动模型复杂,机动性强,常规的目标跟踪方法对该类目标的跟踪性能差,甚至无法跟踪。目前普遍认为最好的高速高机动目标跟踪算法是交互多模型滤波方法,该滤波方法不需要建立准确的目标运动模型,而是采用多个模型的组合来逼近目标的真实运动状态,模型之间的转移概率通过计算滤波残差进行调整。与单模型自适应算法相比,交互多模型算法具有以下显著的优点:
a.由于对参数空间采用的多模型描述,可以通过适当的扩充模型来达到对建模的细化,通过实时的增减和变更模型,可增强变结构的自适应能力;
b.算法的计算量与选用的模型数几乎是线性关系,而其性能与二阶广义伪贝叶斯算法相当;
c.在滤波过程中,通过模型概率的变动实现自适应的变结构;
d.算法具有明显的并行结构,便于并行运算实现。
IMM 滤波中,运动模型的选择直接关系到目标跟踪性能,根据临近空间目标的高速高机动的运动特性和目标模型的特点,本文采用CV 模型、CA 模型和Singer 模型的三模型交互滤波器。
CV 模型将目标的运动先验地定义为匀速,机动被看作是一种随机的输入,其大小体现在过程噪声的协方差矩阵中。
CA 模型是假设加速度的一阶导数是白噪声的过程。
Singer 模型用目标机动幅度和目标机动的持续时间描述一维机动,运动目标的加速度模型不是通常假定的白噪声模型,而是相关噪声模型。
基于CV+CA+Singer 模型的IMM 滤波算法结构[4-5]如图2 所示。

图2 IMM 算法结构图
IMM 算法的递推处理过程如下:
a.状态估计的交互
假设从模型i 转移到模型j 的转移概率为ptij

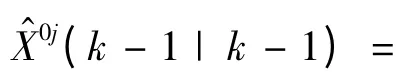

b.模型修正
c.模型可能性计算

d.模型概率更新
模型j 的概率更新如下:

e.输出交互

4 仿真分析
4.1 仿真场景
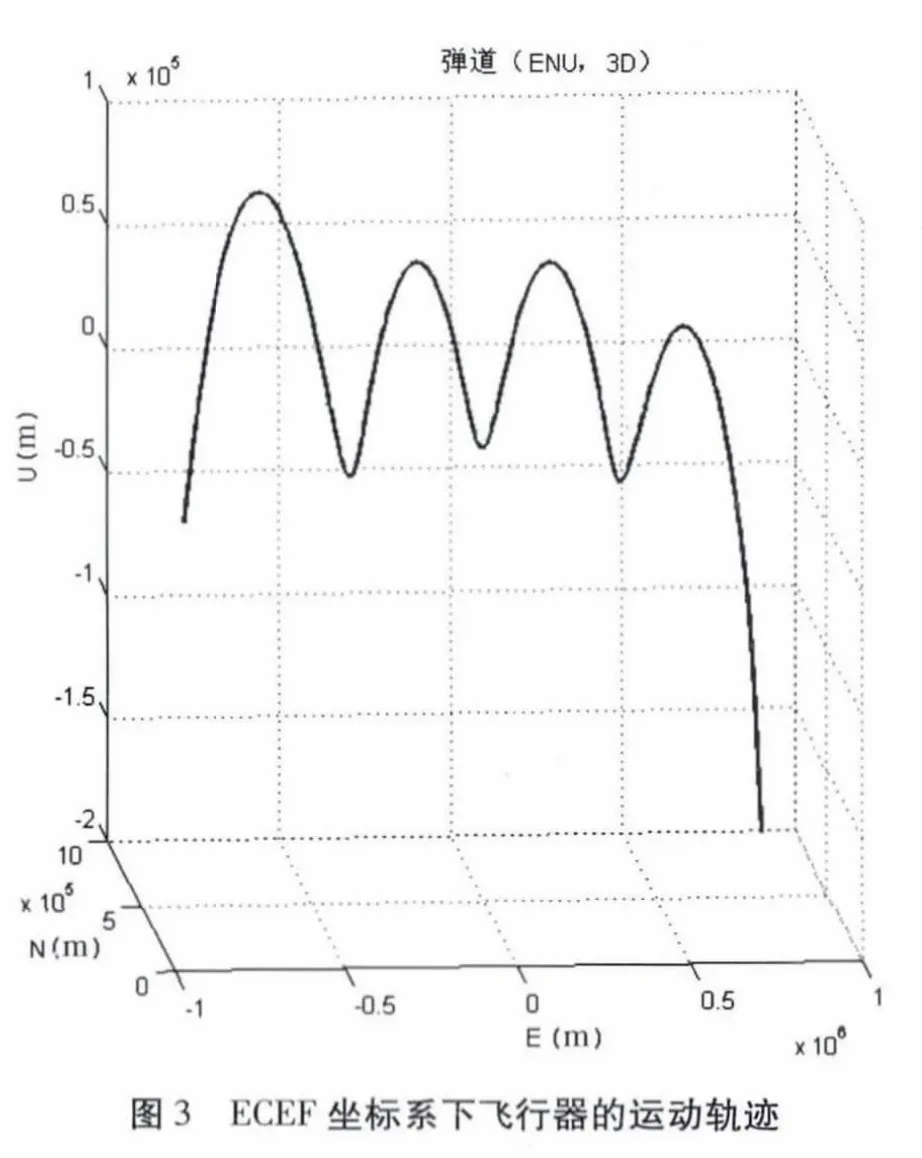
按(1)~(12)的动力学模型,得到临近空间目标在地心固定坐标系中的轨迹如图3 所示。从图中可以看出目标的运动轨迹与实际飞行的轨迹曲线相似,说明本文的建模方法正确。
设定雷达位置,将地心固定坐标系中的轨迹转换为雷达测量的距离、方位、仰角坐标如图4~图6。目标的速度变化曲线如图7。
4.2 仿真结果分析





假设雷达采样数据率为1Hz,距离精度为150m,方位精度为1°,仰角精度为1°,在图4~图6 的理想数据中增加雷达探测误差,产生雷达探测的点迹数据。对此数据应用式(13)~(20)的IMM 滤波算法进行滤波。雷达点迹与滤波后的航迹如图8 所示,滤波后的方位一次差如图9,距离一次差如图10 所示,仰角一次差如图11 所示,经统计计算,滤波后航迹的距离精度为93.8464m,方位精度为0.6571°,仰角精度为0.7205°,明显优于雷达量测点迹。



图8~图11 表明:
a.IMM 算法能够对临近空间目标进行跟踪,验证了该方法在临近空间目标跟踪应用上的可能性;
b.利用IMM 算法进行滤波后所得到的目标航迹精度明显优于通过点迹精度,验证了该方法在临近空间目标跟踪应用上的有效性;
c.本文建立的临近空间高速目标模型轨迹与实际目标飞行轨迹逼近程度较高,能作为雷达算法仿真的输入。
5 结束语
本文对临近空间飞行器进行特性分析和建模,采用IMM 算法对其进行跟踪,仿真结果表明,IMM算法具有较好的临近空间飞行器跟踪性能,跟踪精度提高明显,为雷达进行临近空间目标跟踪提供了一种方法。但本文提供模型未经实际数据比较,模型的准确性还需进一步验证。
[1]肖业伦.航空航天器运动的建模-飞行动力学的理论基础[M].北京:北京航空航天大学出版社,2003.
[2]孙勇.高超声速飞行器再入过程改进气动参数模型[J].系统工程与电子技术,2011,33(1) .
[3]关欣,赵静.一种可行的高超声速飞行器跟踪算法[J].电讯技术,2011,51(8) :81~83.
[4]Mazor E,Aveebuch A,Bar-Shalom Y,et al.Interacting multiple model methods in target tracking:a survey[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1) :103-122.
[5]何友,修建娟,张晶炜等.雷达数据处理及应用[M].北京:电子工业出版社,2009.
