集合扩充的社团分解算法

李圆媛，余汪建，何敏华

（1.武汉工程大学理学院，湖北 武汉 430074；2.智能机器人湖北省重点实验室，湖北 武汉 430074）

0 引 言

二十世纪末以来，随着Internet等信息技术的迅猛发展，人类社会已经进入了网络时代［1］，人们也把目光聚焦到复杂网络的研究上来.近些年来，复杂网络研究渗透到了各个领域，科学的理解复杂网络的各种定量与定性的特征是网络时代的一个非常有挑战性的科学研究课题［2］.

许多真实网络研究显示绝大部分的网络存在一个相同的特征，被称之为网络中的社团结构.它是指网络中的全部节点可以被划分成若干个群体，每个群体里面的节点的连接相对稠密，而群体之间的节点的连接相对稀疏［3］.对网络中社团结构的研究是了解整个网络结构和功能的重要途径［4］.

1 网络图的定义和基本概念

对网络进行社团分解的操作是基于网络图的表示，在介绍复杂网络的社团分解算法前首先介绍网络图的定义和基本概念.网络图G可以用集合（V，Ψ）表示，V（G）＝｛1，2，...，N｝表示网络图G的节点集合，N表示网络图的节点总数，Ψ（G）＝｛（i1，j1），（i2，j2），...，（iE，jE）｝表示边的集合，用E 表示边的总数目，若（i，j）＝（j，i）则该网络图被称为无向网络图，反之则被称为有向网络图，在本文中只讨论无向无权网络图.无向无权网络图的邻接矩阵A（i，j）是一个对称的0－1矩阵，如果节点i，j之间有联系则ai，j＝1，否则为0.对于一个节点i的度定义为与节点i相连接的边的数目.

2 社团分解算法综述

现在对于复杂网络的社团分解有许多成熟的方法，如基于图的Laplace矩阵特征向量的谱平分法［5］，GN 算法［3］、NF算法［6］等.一个 有n 个节点的无向图G的Laplace矩阵是一个n×n维的对称矩阵L，理论上已经证明，不为零的特征值所对应的特征向量的各元素中，同一个社团内的节点对应的元素是近似相等的.谱平分法的基本思想就是根据网络的Laplace矩阵的第二小的特征值λ2将网络分成两个社团.如果网络实际是由两个社团构成，用谱平分法效果很好，但是如果由多个以上的社团构成，则体现不出其优点.GN算法是Girvan和Newman提出的一种探索网络社团结构的分裂算法.Girvan和Newman提出用边介数来标记每条边对网络连通性的影响.GN算法能够弥补一些传统算法的缺陷，但是在复杂网络中社团的数目未知的情况下，GN算法无法确定这种分解要在哪一步终止.GN算法虽然准确度比较高，但是其算法复杂度比较大，Newman在GN算法的基础上基于贪婪算法思想提出了一种快速的凝聚算法 （简称NF算法），该算法可以用于处理节点数达到100万的大型网络［7］.

3 集合扩充的社团分解算法

3.1 算法原理

对复杂网络进行社团分解的本质就是要找出某些节点联系是紧密的，对于每一个点来说，它必可以划分到一个联系最紧密的点集中，在这里需要做的就是判断每个点是否和某个社团联系紧密，如果是，那么该点就可以划分到这个社团中.

假设有了一个节点的集合S＝（V，G），V表示该集合中的所有节点，G表示该集合中节点间的边.现在对于一个新的节点vn，为了判断vn是否可以加入集合S，先定义一个参数：PQ＝oe／ie，式中的oe表示一个节点在S内而另一个节点不在S中的边的总数，ie表示S中的边的总数.该式的物理意义就是社团同外部联系的边的数目与社团内部边的数目的比值.在此先计算PQ（S），再计算出加入点vn之后的PQ（Sn），如果PQ（Sn）＜ PQ（S），那么就认为vn和集合S＝（V，G）的联系是比较紧密的，就把节点vn加入到集合S＝（V，G）中来.

3.2 算法流程

参照算法原理，给出该算法如下运行流程：

步骤一：在已知的节点集中选取一个度最大的节点，找到与该点有关联的所有节点，选取其中一个度最小的点，和第一个节点构成一个集合.

步骤二：对于步骤一中得到的集合，找到与该集合相关的所有节点，分别计算这些节点加入该集合后的PQ值并和之前集合的PQ值进行比较，判断能否加入该集合，如果可以加入，则加入该集合.

步骤三：重复步骤二，将这个两点的集合不断的扩充，直到整个网络中剩余的点都不符合加入该集合的条件为止，这样就得到了划分出来的一个社团.

步骤四：从网络图中去掉已经找出的社团，重复步骤一、步骤二、步骤三直到网络中的节点完全划分.

3.3 算法分析

这个算法的优点是不需要考虑整个网络的结构，划分的思维比较清晰，同时可以根据不同的需求对网络进行不同的划分.在某些网络中，并不需要对整个网络进行社团结构划分，只是需要找出其中的部分社团，在这种情况下，运用笔者提出的算法具有运算简便、运算量小的特点.而GN算法和NF算法在运算的时候都需要考虑整个网络的拓扑结构，运算量很大.同时本文的算法可以通过调整起始规则或者起始集合来得到不同的社团结构划分.同谱平分算法相比，笔者提出的算法可以将整个复杂网络分成任意个社团结构，而谱平分法仅能将网络分成两个社团.

3.4 算法测试

为了测试程序的正确性和算法的可行性，构造了一个社团结构很清晰的网络图，如图1所示.从图中可以很清楚的看到该网络可以划分为四个比较合理的社团.将四个社团以节点集合的形式表现出来为（11，12，24，27，29，16，28，22），（6，8，18，19），（9，21，17，7，3，23，25），（1，4，15，2，5，30，20，13，14，26，10）.先将该网络的邻接矩阵进行存储，然后应用笔者提出的算法，得到如表1所示的结果.从该表中看到，算法也将网络分成了四个社团，并且结果与预期的一致，那么说明文中提出的算法在此社团结构比较清晰的网络中是可以实现的.

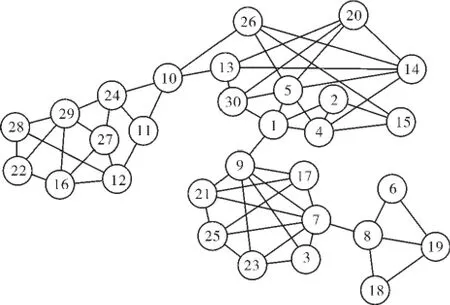
图1 社团结构清晰的网络图Fig.1 Aschematic representation of a network with community structure

表1 图1的测试结果Table 1 The test results of figure 1

为了进一步测试算法的可行性，使用了著名的Wayne Zachary观察的美国大学空手道俱乐部成员间的人际关系网络的例子［8］，如图2所示，该例子具有很强的实际意义，把该例子应用到笔者提出的算法程序测试中来，将该网络的邻接矩阵进行运算后得到如表2所示的结果.从表2中看到该算法将网络分成了两个社团，第一个社团和图2中圆形表示的社团基本符合，第二个社团和图2中方形表示的社团基本符合.除了节点3的划分和GN算法的划分有区别外，其余的结果和使用GN算法的结果一致.从直观上来说，也不能确定节点3到底分在哪一个社团比较合适，这说明笔者提出的算法在结构不是很清晰的实际网络中进行社团划分还是具有一定意义的.

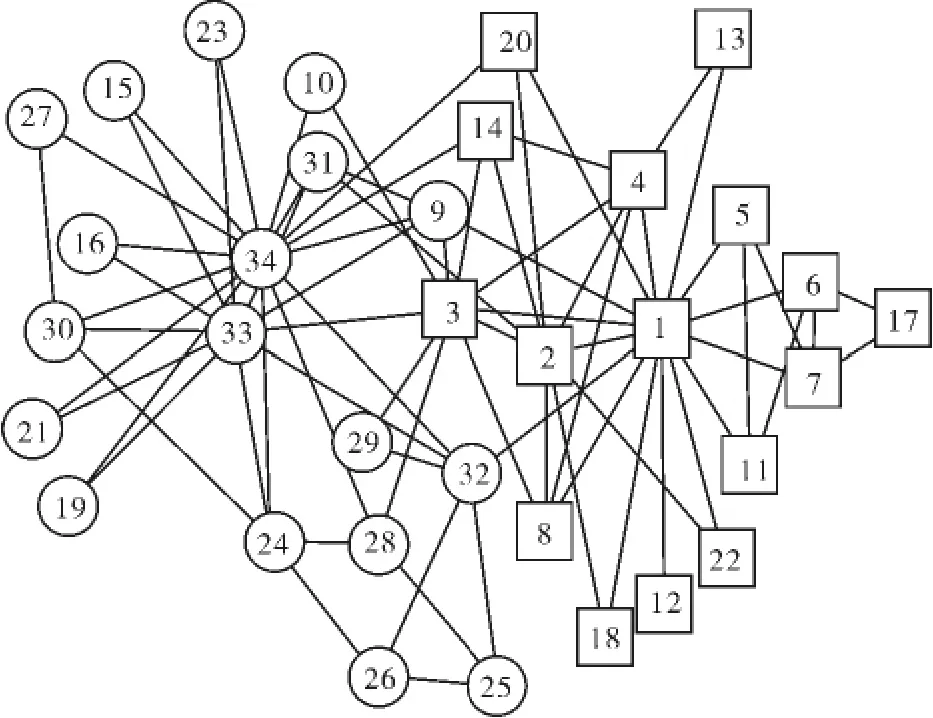
图2 空手道俱乐部网络图Fig.2 The friendship network from Zachary＇s karate club

表2 图2的测试结果Table 2 The test results of figure 2

4 结 语

复杂网络的社团结构分解是一个富有挑战性和应用前景性的研究领域.本文提出了通过集合扩充的方式划分复杂网络中社团结构的算法.并对提出的算法进行了详细的介绍，给出了算法的理论基础和算法流程，并对算法进行了实例测试.从测试结果可以看出，本文提出的基于集合扩充的社团分解算法具有不错的效率，本文中仅仅讨论了复杂网络社团分解算法在无向无权图中的运行，而现实生活中很多实际网络都是有向的有权的.因此如何定义和划分有向网中的社团结构，有向网中的环型结构与集团结构的关系，以及如何探索有向网中的层次问题都是一些值得我们关注的问题.

［1］汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.北京：清华大学出版社，2006.

［2］Barabasi A L，Frangos J.Linked：The New Science of Networks［M］.Massachusetts：Perseus Books Group，2002.

［3］Girvan M，Newman M E J.Community structure in social and biological networks［J］.Proceedings of the National Academy of Sciences of the United States of America，2001，99（12）：7821－7826.

［4］李晓佳，张鹏，狄增如，等.复杂网络中的社团结构［J］.复杂系统与复杂性科学，2008，5（3）：20－42.LI Xiao－jia，ZHANG Peng，DI Zeng－ru，et al.Community Structure in Complex Networks［J］.Complex Systems and Complexity Science，2008，5（3）：19－42.（in Chinese）

［5］Pothen A，Simon H D，Liou K P.Partitioning sparse matrices with eigenvectors of graphs［J］.SIAM Journal on Matrix Analysis and Applications，1990，11（3）：430－452.

［6］Newman M E J.Fast algorithm for detecting community structure in networks［J］.Physical Review E，2004，69（6）： 066133－ 066137.

［8］Zachary W W.An information flow model for conflict and fission in small groups［J］.Journal of Anthropological Research，1977，33（4）：452－473.