一种改进的粒子滤波算法

倪春光

(91388部队，广东 湛江524022)

0 引言

对于非线性系统状态估计问题，当噪声是高斯时，传统的解决方法是扩展卡尔曼滤波 (EKF)和无迹卡尔曼滤波 (UKF)。当噪声是非高斯时，人们提出了粒子滤波 (PF)、无迹粒子滤波 (UPF)等。PF是一种基于蒙特卡罗方法的贝叶斯状态估计算法，通过一组归一化权值的粒子来近似表示后验概率密度，其建议分布是先验概率密度，具有计算简洁的特点，但由于其建议分布没有包含新的测量信息，其粒子的使用效率不高。而UPF采用UKF来计算建议分布，其中UKF对高斯随机变量的均值和方差可以精确到三阶，并结合新的测量信息，可以使建议分布更好地逼近后验概率密度，但是运算量很大。

本文提出一种新的粒子滤波 (MUPF)，与传统的UPF相比，它介绍了一种辅助模型并且利用辅助模型和UKF来产生粒子的建议分布，从而提高计算的精确度。

1 粒子滤波

1.1 贝叶斯估计原理

假定动态时变系统可描述为

系统方程:

量测方程:

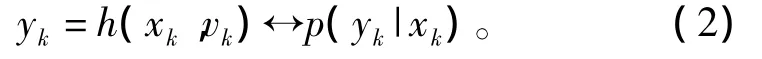
若已知状态的初始概率密度函数p(x0|y0)=p(x0)，则状态预测方程和状态更新方程分别为

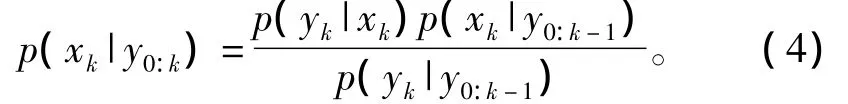
其中 p(yk|y0:k－1)=∫p(yk|xk)p(xk|y0:k－1)dxk，由于其积分的复杂贝叶斯递归滤波很难实现，如果系统为高斯线性空间模型，可以通过卡尔曼滤波得到最优的状态估计。对于非高斯非线性系统，如何快速计算积分是研究滤波算法的核心问题。

1.2 粒子滤波算法

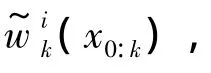
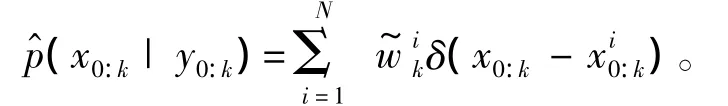
当无法从后验分布p(x0:k|y0:k)中直接采样时，可以找一个容易采样的密度分布函数q(x0:k|y0:k)(建议分布)中采样。

令w(x0:k)为重要性权值:

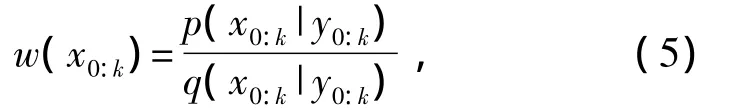
对任何可积函数的期望可以近似为

PF的实现步骤如下:

1)初始化k=0

2)计算重要性权值

粒子权值更新方程:

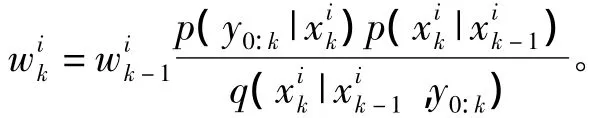
3)归一化重要性权值

4)重采样

5)返回状态估计值

随着迭代次数的增加，重要性权值的分布变得越来越倾斜，有可能出现粒子匮乏现象，为了避免粒子匮乏，Goden等提出了重采样方法，其主要思想就是去掉那些权值小的粒子，复制权值大的粒子。

2 UPF原理

3 一种新的UPF滤波算法

称式(1)和式(2)为主模型，这里主要介绍一种辅助模型并使用UKF和它共同来产生建议分布。

3.1 辅助模型

定义辅助模型为

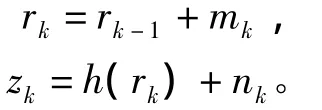
其中:mk为一个小方差高斯噪声，观测噪声nk和式 (2)中的vk认为是一样的。如果h(·)是线性的，nk是高斯噪声，卡尔曼滤波就可以对rk进行最优估计。在实际环境中，h(·)往往是非线性的，可以使用UKF来对rk进行估计。

3.2 MUPF算法

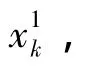
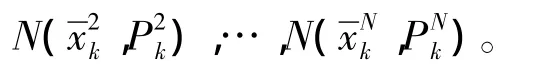
MUPF的算法步骤如下:

1)初始化

2)重要性采样

3)重要性权值

当i=2，…，N时，

归一化权值

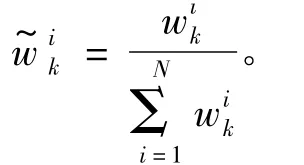
4)重采样

4 仿真试验

为了证明MUPF的性能，考虑一个非线性非高斯模型。

其中，w=4e-2，uk服从Gamma(3，2)分布，观测噪声vk服从高斯分布N(0，10-5)，目标的初始状态x0=1，经过100次蒙特卡罗仿真，每次仿真时间是60 s，采样间隔为1 s。1次独立试验的均方根误差定义为

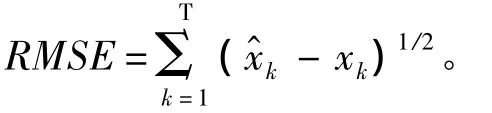
图1表示MUPF使用20个粒子与其他滤波器对系统的状态估计，图2为采用EKF，UKF，PF，UPF及MUPF滤波算法对状态估计的均方根误差曲线图。

表1给出了粒子数为20的时候，各个滤波器的RMSE。

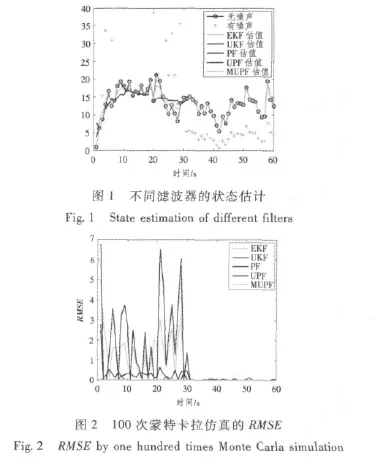
表1 RMSE的均值和方差Tab.1 Mean value and variance of RMSE

5 结语

本文提出了一种新的粒子滤波算法 (MUPF)用来估计非线性非高斯系统的状态。一般情况下，粒子滤波的主要问题是对建议分布的选择，它很大程度上决定着滤波的性能。UPF通过UKF的一步预测来构建建议分布，由于UKF存在缺陷，使得建议分布不能与后验概率密度得到很好的近似。MUPF通过使用辅助模型与UKF来构造建议分布，更好地逼近了后验概率密度。仿真结果表明，新的粒子滤波算法使用很少的粒子就可以达到很高的精度。

［1］ARULAMPALAM M S，MASKELL S，GORDON N.A torial on particle filters for online nonlinear/non-Gaussian Bayesial tracking［J］.IEEE Trans，Signal Process，2002，5(2):174-188.

［2］MERWE R V.A Doucet the Unscented Particle Filter A-dvances in neural Information Proceesing Systems［Z］.MIT，2000.