船舶在风、流环境下的操纵性数字模型
2013-10-20于升杰朱克强赵金鹏沈小龙张长永
于升杰,朱克强,赵金鹏,沈小龙,张 亚,张长永
(宁波大学海运学院,浙江宁波315211)
0 引言
船舶作为水上运输的一种工具,和其他运输工具一样,它的安全性和经济性[1]是最为重要且最为令人关注的性能。船舶操纵性[2]是船舶安全航行的一种重要性能,它对于航运安全有非常重要的影响。尤其是近些年来,随着航运业的迅速发展。船舶吨位急剧增大,船舶航速不断提高,航道的拥挤,使船舶航运安全问题变得尤为突出。同时,现代海难事故造成巨大的人员伤亡和财产损失,而大部分原因是由于驾驶员对船舶操纵性掌握不够,且不能及时准确地应对海上突发状况造成的。对于船舶操纵性研究的主要方面是船舶保持和改变其航速、航向及位置的能力[3],与航行的安全性与经济性密切相关。
船舶操纵包括3种含义:保持航向、改变航向和改变航速[4]。船舶的操纵性预报是在船舶的初始设计阶段,根据包含船舶 (包含螺旋桨和舵)的各项参数,计算出来的船舶操纵性能参数,使设计者对于船舶操纵性能[5]具有一个量化的指标,从而判断出船舶操纵性能的好坏,这也是对于船舶操纵性研究的主要目的之一。
1 船舶运动的水动力模型
1.1 MMG模型
MMG模型是由日本船舶操纵运动数学模型小组提出,其主要研究方法是根据各项流体动力的成因及物理意义,将其表达为分别作用在船体、螺旋桨、舵上的流体动力及其间的相互干扰,是一种水动力模型,属于非线性数学模型[7]。主要用于船舶回转过程和各种激烈操纵运动时的数学模拟,其模拟计算结果的精确度明显高于线性模型。
1.2 MMG模型中采用的坐标系
MMG模型仅考虑船舶在静水面的水平操纵运动情况,假定船舶航行在无限深广的水域,船体为刚体,忽略船舶摇荡[8]的影响。建立2个坐标系:一个是固定坐标系O0-x0y0,固连于地球;另一个是运动坐标系G-xy,固连于船体。

图1 双坐标系下的船舶运动Fig.1 Ship moement in bi-coordinate system
1)根据坐标系建立的运动方程
在运动坐标系中船舶运动方程式 (为避免寻找重心的麻烦,将坐标系的原点记于船中处)为
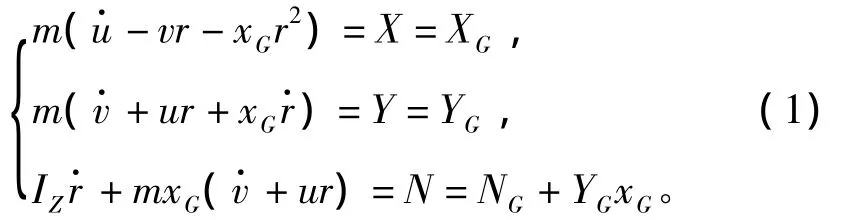
式中:XG为船舶在船前进方向所受的力;YG为船舶垂直于船舷方向所受的力;IZ船体绕船体重心的转动惯性矩;NG船舶绕船体重心的转动力。
1.3 MMG模型的无因次化
因为无因次化采用的特征量并未统一,MMG采用如下方法无因次化:
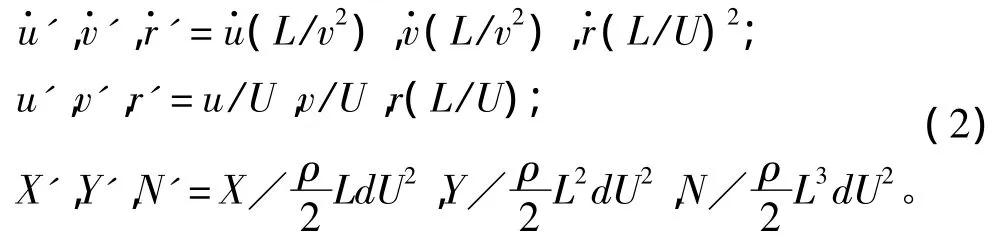
1.4 MMG模型考虑船桨舵
MMG模型中,作用于船上的水动力以船体、螺旋桨和舵各自所贡献分量之和的形式表示,即
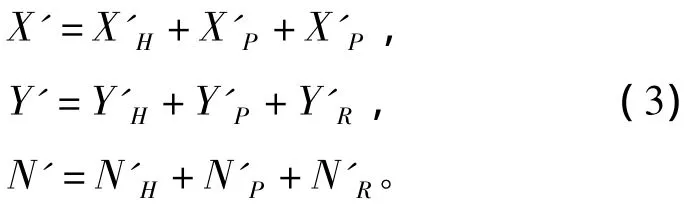
式中的下脚H代表船体,P代表舵,R代表舵。
1.5 附加质量
采用周昭明根据元良图谱而进行的多元回归分析得到的公式来计算附加质量与附加惯性矩:
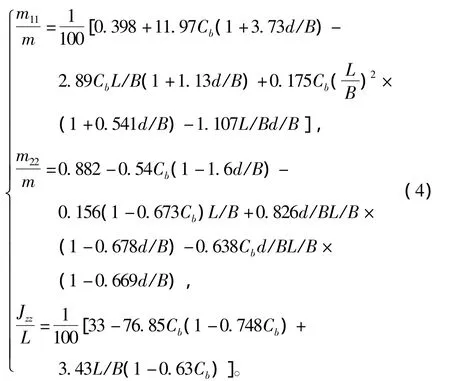
式中:L为船长;d为吃水;Cb为方形系数。
1.6 船舶操纵运动方程
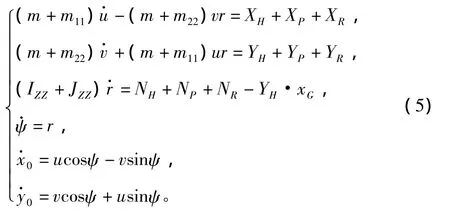
式(5)中所需的各个量均可以由上述模型中求得,最后求得静水中船舶的航向角ψ,以及船舶的重心坐标G(x0,y0),可以根据VB编程得到船舶在静水中的操纵运动曲线。
2 风、流模型
2.1 流压模型
在均匀流场下考虑流体对船舶运动的影响是将流速Ve分解到船舶动坐标系的Gx和Gy轴,可得:
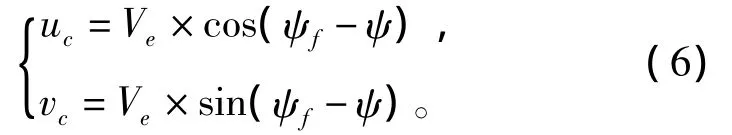
式中:uc为流速Ve在Gx轴上的分量;vc为流速Ve在Gy轴上的分量;ψf为流向角 (从真北为0°开始顺时针计算,与航海中流去的方向一致);ψ为船舶的航向角。
则船舶对地速度(考虑流以后)在Gx,Gy轴上的分量u1,v1分别表示为:

至于船舶的摇首角速度r无论是对水或是对地都保持不变。对式(7)关于时间t求导可以得到加速度之间的关系:

2.2 风压模型
风对船的作用力大小主要与船的上层建筑及其布局、风向和风速大小有关,其关系如下 (风压保持不变):

式中:ρa为空气密度;Ar,AL分别为船舶水线以上船体的正投影面积和侧投影面积;VW,θr分别为相对风速和相对风舷角;CWX,CWY,CWN为纵向风压力系数、横向风压力系数及力矩系数,数值由风洞试验得,若无实验数据,可由Isherwood的回归方程求得。
3 船舶在各种情况下的旋回圈及分析
3.1 左旋回与右旋回特性
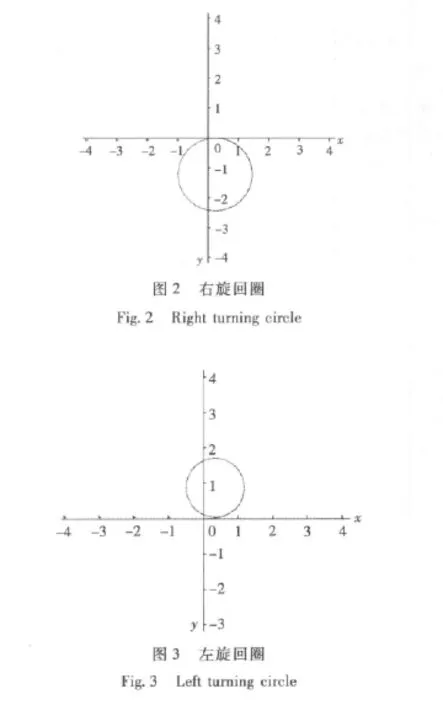
船舶转舵前做等速直航运动,然后转舵使舵角δ分别为35°与-35°。如图2和图3所示,当船舶舵角δ=35°(右满舵)比δ=-35°(左满舵)时船舶的回转圈要大,由于船舶自身存在操作的灵敏度和惯性力问题,船舶向左转与向右转其回转圈大小不一样,且右舵回转圈更大。
3.2 流影响下的回转性能
船舶在操舵前保持等速直航,操舵后舵角δ=35°,且流速 Ve=2 m/s,流向 ψf=90°。
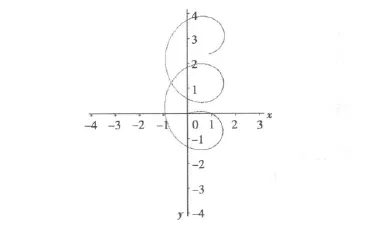
图4 仅考虑流作用的回转圈Fig.4 Turning circle only concerned flow influence
在均匀流场中,船舶对水的旋回运动情况与静水中相同,也就是说船舶对水的回转圈大小不变。但对地回转圈却在流的方向上漂移,且漂移速度等于流速。所以流越急,这种漂移引起的变形也就越大。因此船舶在受限水域内转向一定要考虑流的影响,在静水中操作时可以参考船舶旋回性试验资料,在有流水域内,一般顺流操舵时机应适当提前,逆流操舵时机应适当滞后。
3.3 风影响下的回转性能
船舶在操舵前保持等速直航,操舵后舵角δ=35°,且风速 VW=2 m/s,风舷角 θr=90°。
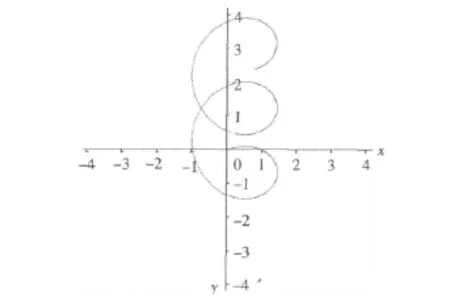
图5 仅考虑风作用的回转圈Fig.5 Turning circle concerned wind influence
当船舶受到了风舷角θr=90°的风力后,船舶成螺旋线形向上运动,由于风是具有阵性所以船舶受力按一定规律变化,轨迹图上重心点的疏密情况也不同。本文试验数据参照“育英”轮模型的风洞试验。
4 结语
1)船舶左旋回圈和右旋回圈的大小不一样,且右旋回圈更大。即左舵和右舵操纵性能不一样,操舵时应充分考虑其差异。
2)在均匀流场中,船舶对水的旋回运动情况与静水中相同,即回转圈大小不变。
3)在有流水域内船舶会随水流一起漂移,所以一般顺流操舵的时机应适当提前,逆流操舵的时机应适当滞后。
4)在受风环境下船舶运动轨迹上的点的疏密不同 (由于风具有阵性,风力大时船舶运动速度高,计算机上显示的点较疏,相反显示的点较密)。
[1]吴秀恒,刘祖源,等.船舶操纵性[M].北京:国防工业出版社,2005.WU Xiu-heng,LIU Zu-yuan,Ship Maneuvering[M].Beijing:National Defence Industry Press,2005.
[2]贾欣乐,杨盐生,船舶运动数学模型——机理建模与辨识建模[M].大连:大连海事大学出版社,1997.JIA Xin-le,YANG Yan-sheng.MathModelofShip Movement—Mechanism Modeling and Distinguish Modeling[M].Dalian:Dalian Maritime University,1997.
[3]洪碧光.船舶操纵[M].大连:大连海事大学出版社,2008.HONG Bi-guang.Ship Maneuvering[M].Dalian:Dalian Maritime University,2008.
[4]SUTULO S,MOREIRA L,et al.Mathematical models for ship path prediction in manoeuvring simulation systems[J].Ocean Engineering,2002,29:1-19.
[5]蒋维清.船舶原理[M].大连:大连海事大学出版社,1998.JIANG Wei-qing.Ship Maneuvering[M].Dalian:Dalian Maritime University,1998.
[6]TRIANTAFYLLOU M S.Cable dynamic for offshore applications(Chapter 6)[D].Department of ocean Engineering Massachusetts Institute of Technology,Cambridge,Massachusetts,USA.
[7]乐美龙,陆惠生,汪希龄,等.船舶操纵模拟器操纵仿真数学模型[J].中国航海,1999(1):77-86.LE Mei-long,LU Hui-sheng,WANG Xi-ling,et al.Ship manuvering simulation math mode[J].China Navigation,1999(1):77-86.
[8]冯铁成,朱文蔚.船舶操纵与摇荡[M].北京:国防工业出版社,1989.FENG Tei-cheng,ZHU Wen-wei.Ship Manuvering and Rolling[M].Beijing:National Defence Industry Press,1989.
