超空泡射弹尾拍问题研究进展
2013-10-20魏英杰何乾坤张嘉钟
魏英杰,何乾坤,王 聪,曹 伟,张嘉钟
(哈尔滨工业大学航天学院,黑龙江哈尔滨150001)
1 概述
航行体在水下高速运动时,航行体表面附近的水因低压而发生相变,产生空化现象。当航行体的运动速度足够高时,空泡将完全包裹航行体形成超空泡。超空泡减阻技术是一种可以使水下高速运动航行体获得90%减阻量的革命性减阻方法[1]。利用这种技术研制的超空泡射弹,可以显著提高射弹的运动速度,大大增加射弹的行程和杀伤力[2]。
超空泡射弹目前主要应用于反水雷和反鱼雷作战,通常有2种作战方式。一种是通过水面舰载或机载火炮发射,以高速入水打击水下目标,如美国的机载快速灭雷系统[3](简称RAMICS,如图1所示)主要装备于直升机机载火炮系统中,用以消灭水下30 m深的浅水锚雷或漂雷,也可作为一种对付反舰鱼雷的硬杀伤防御武器;另一种是全水下火炮系统,采用超空泡射弹密集发射的方式拦截来袭的敌方鱼雷,如美国的自适应高速水下弹药系统(AHSUM)主要装备在潜艇、水面舰或拖曳式反水雷器的水下船体内。

图1 RAMICS超空泡射弹示意图Fig.1 Scheme of supercavitating projectile RAMICS
高速超空泡射弹在水下运动过程中,任何小的扰动 (如发射时的扰动)都会使射弹尾部与空泡汽水界面发生连续的周期撞击,即尾拍现象[4]。May[5]早在1975年的AD报告中就阐述了超空泡航行体尾拍现象形成的原因,并且分析了尾拍现象对稳定航行体弹道起到的作用。高速超空泡射弹具有大长细比 (一般在1∶20左右)以及运动速度高的特点[6-9],因此射弹结构的稳定性和可靠性必须予以考虑。高速运动下的尾拍问题涉及流体动力学、结构运动学及动力学问题,因此如何对尾拍问题进行合理的数学建模显得非常重要。
本文综述高速超空泡射弹尾拍问题的研究进展,分析超空泡射弹尾拍研究中涉及的关键问题,并对超空泡射弹尾拍问题未来的研究方向进行展望。
2 研究进展
从上个世纪90年代末开始,针对超空泡射弹的尾拍问题,国内外学者开展了一系列的理论和实验研究工作,在空泡形态、尾拍载荷及尾拍动力学模型方面取得了重要研究进展。
2.1 国外研究进展
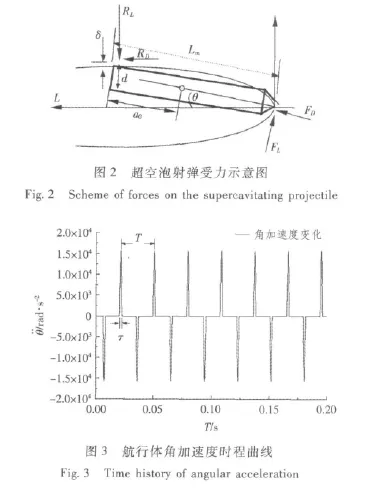
Rand等[10-11]建立了射弹在垂直平面内尾拍时的简化模型,假设射弹头部近似沿直线L运动、空泡轴线与L重合 (见图2),考虑到超空泡射弹运动速度较高,忽略重力对空泡形态的影响[5]。并且,假设射弹头部受流体升力和阻力的合力沿射弹轴向,尾部受到尾拍阻力RD和升力RL作用,得到射弹刚体动力学方程。其中,尾拍过程表达为方程 (1),尾拍结束后表达为方程 (2)。
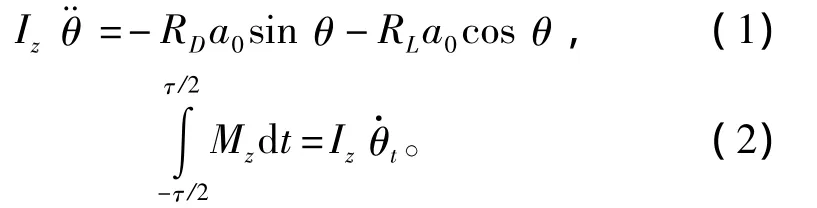
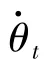
根据式(1)和式(2)可以确定航行体在航行状态中发生尾拍的振动方式。Rand在假设θ为小量的基础上给出了超空泡射弹尾拍的角频率ω和尾拍振动半周期τ的表达式为
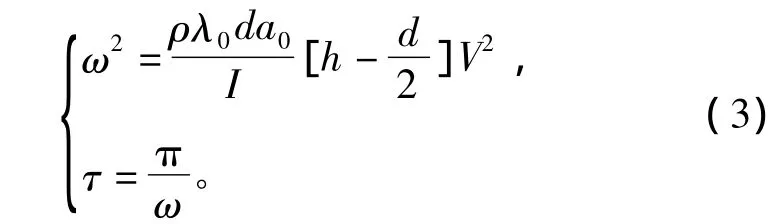
式中:ρ为水密度;λ0=0.5为经验常数;d为射弹尾部直径;h为射弹尾部处超空泡半径。如图3所示为角加速度振动,图中T定义为航行体整体振动周期,τ定义为尾拍振动半周期。
Kulkarni[12]等研究了超空泡射弹的尾拍刚体动力学特性,基于Milwitzky[13]的水上飞机撞水受力方式分析了射弹尾拍受力并建立了超空泡射弹尾拍刚体动力学方程,并在此基础上进行仿真计算。结果表明,尽管超空泡射弹的尾拍现象会影响射弹弹道,但射弹基本上保持直线飞行;射弹减速运动过程中,尾拍撞击的频率先增加后减小;对于具有不同转动惯量的超空泡射弹,尾拍频率随弹体转动惯量的增加而变小。
Ruzzene[14]等将超空泡射弹考虑为绕空化器转动的欧拉-伯努利梁,射弹具有俯仰、偏航2个刚体转动自由度和2个径向挠度,并基于哈密顿原理建立了超空泡射弹尾拍的柔性多体动力学方程,对射弹的弹性振动位移响应与刚体转动响应进行了计算分析。在此基础上,Ruzzene还对超空泡射弹的加固模型进行了分析,给出了环状加强筋的厚度大小和安装数量对弹性振动的影响。
Choi[15]利用模态单元法 (Modal-Based Elements)建立了超空泡航行体的刚柔耦合动力学方程,并解除了航行体空化器近似沿水平运动的假设,分析了航行体尾拍或滑行过程中尾部撞水载荷,计算了超空泡航行体的刚体运动及结构振动,并对航行体弹道进行了良好的控制。
Abe[16]使用显式动力学有限元分析软件AUTODYN对水下超音速自由飞行超空泡射弹初始时刻的偏航问题进行了数值仿真研究。Abe建立了二维计算模型,研究了射弹高速入水后,可能导致弹体发生偏航的因素。仿真结果表明:弹体入水速度越大,弹体的偏航角越大,弹体速度衰减得越快;对于不同材料射弹入水,射弹的材料为钛时比材料为钢时发生偏航要早;弹体和水的周围固体边界对弹体的速度变化和偏航具有较为显著的影响。
Putilin[17-18]对超空泡射弹入水及水下运动进行数学建模,分析了超空泡射弹与空泡之间的间隙对超空泡射弹入水及水下减速过程中的尾拍运动特性影响。而Kubenko[19]进一步研究了细长超空泡航行体与超空泡壁面撞击载荷计算。Kubenko将水考虑为可压缩理想流体,并且分析了不同航行体与空泡间隙Δ下的撞击载荷计算公式,其中Δ=1-r/Rc,r和Rc分别是航行体和空泡的半径。对于不同的间隙Δ(分别为零间隙、小间隙及大间隙),建立了描述圆柱形航行体尾部浸入空泡壁面的动力学方程,并利用渐进法进行简化求解。
Ziraksaz[20]探讨了在小型超空泡射弹上安装微型固体燃料引擎来提高射弹飞行速度的可行性以及超空泡射弹在相应的结构设计上需要注意的问题。该研究工作为进一步提高射弹飞行速度提供了一种途径。
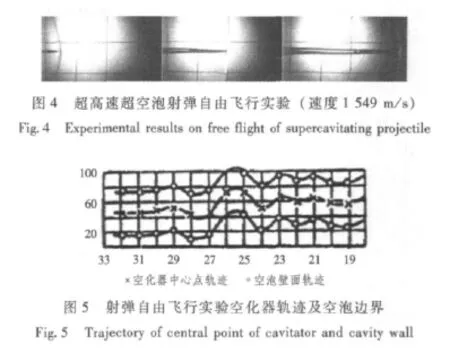
Kirschner[21-22]和 Hrubes[23]对不同发射速度下的超空泡射弹进行了大量的实验分析,记录了超空泡射弹在超音速自由飞行过程中的空泡形态和尾拍特性 (见图4)。Kirschner[22]还在高速超空泡射弹动力学控制方面引入了空泡延迟效应,分析了空泡延迟对超空泡航行体的流体动力影响。
Vlasenko[24]对跨音速和超音速阶段的超空泡射弹进行了自由飞行实验,分析了水的可压缩性对空泡形态的影响。
Logvinovich[25]对超空泡射弹自由飞行进行了实验分析,记录了射弹在尾拍过程中头部坐标,描绘了除了射弹S形运动轨迹 (见图5)。
2.2 国内研究进展
国内方面,孟庆昌等[26]对超空泡射弹进行了刚体动力学分析,参考了Kulkarni[12]的文章中有关超空泡形态以及受力模型的推导结果,建立了描述弹体动力学行为的微分方程组。基于该方程组,分析了超空泡射弹的转动惯量、发射速度、初始扰动角速度和水深对超空泡射弹尾拍弹道的影响。研究结果表明:射弹尾拍过程中的角速度大小呈现周期性的往复变化;射弹转动惯量越小,角速度变化幅值增减越小,尾拍撞击频率越小;射弹发射深度或发射速度越大,尾拍最大转角衰减得越快;较大的初始角速度会使射弹角速度发生快速的衰减。
潘展程等[27]针对超空泡航行体纵向振荡时,流场及阻力系数的变化,进行仿真研究。采用二维轴对称计算模型,航行体做正弦规律的受迫纵荡,利用有限体积法求解Reynolds平均N-S方程组,基于Mixture多相流模型,分别采用非惯性系法、动计算域法、滑移网格法以及网格重构法对该种情况下的通气超空泡流场进行计算。结果表明:阻力系数在周期纵荡运动过程中也出现了周期性的振荡。同时,经过对各种方法的比较,发现动计算域法的计算量小,收敛性好,精度高,最适合用来对带超空泡航行体做非定常运动进行模拟。
张鹏[28]使用Fluent 6.3的UDF功能,研究了射弹在水中跨超音速下产生的超空泡流场。在Mixture模型下分别计算了水不可压和可压2种状态下超空泡射弹的流场,并对2种状态下流场做了对比分析,表明在跨超音速下,水的可压缩性会增加射弹的阻力。另外,模拟了可压单相流的射弹流场,得出射弹周围温度场的分布,结果表明射弹运行的结果会产生大量的热。
杨传武等[29-30]针对匀速直线运动的超空泡航行体 (以直径210 mm鱼雷为参照)的尾拍结构动力学响应问题进行了有限元仿真研究,将航行体考虑为壳模型,对尾部的尾拍冲击载荷形式采用Ruzzene[14]的理论结果。作者对航行体尾部位置的加速度响应进行了计算,并进行了频响分析。结果表明:冲击载荷作用方向引起的过载非常大,达到了30 g;超空泡航行体垂向振动频率在20 Hz以内时引起的结构响应最为显著,随着频率的升高加速度响应的幅值有减小的趋势。
张劲生[31-32]、何乾坤等[33]对超空泡射弹在尾拍过程中的载荷以及动力学响应进行了数值模拟,分析了射弹长径比对射弹弹性振动过程中的应力、应变影响。研究结果表明:航行体与空泡碰撞期间,航行体尾部变形最大;当航行体脱离空泡壁面,做高频振动期间,其头部和柱体中部变形最大;在不同速度条件下,航行体的最大主应变和最大剪应变都随着速度的增加而呈上升趋势,最小主应变值(压应变)也随着速度的增加而变得更小。
曹伟等[34]开展了水下超空泡射弹运动的模型试验,射弹最大速度为70 m/s,最小空化数可达0.04,获得了水下航行体的自然超空泡形态参数随空化数变化的规律,并与相关文献中使用的经验公式进行了对比。
3 超空泡射弹尾拍问题涉及的关键问题
超空泡射弹尾拍分析涉及流体动力学、结构运动学及动力学等多方面内容。在流体动力学分析方面,涉及超空泡形态以及尾拍撞击载荷的确定;在尾拍刚体动力学和结构动力学方面,超空泡射弹的运动是刚体运动与弹性体运动的耦合问题,可以看作是柔性多体动力学问题,该问题与流体动力学分析结合在一起,将更加复杂。
3.1 超空泡形态分析
超空泡形态分析作为超空泡射弹尾拍问题的一部分,将直接影响超空泡射弹尾拍计算。以往的超空泡射弹尾拍文献中对空泡形态的确定往往采用经验公式。如 Kulkarni[12]和 Choi[15]利用椭圆形空泡半经验渐进解公式
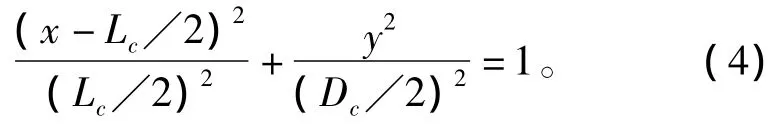
式中,空泡最大截面直径Dc及空泡长度Lc表达为

式中:σ为空化数;Dn为空化器直径;Cx0为σ=0时的阻力系数。经过实验验证[35],式(5)对于圆盘空化器的适用范围在300~1 300 m/s。
对于非定常超空泡形态的确定可以利用Logvinovich 独立膨胀原理[36-37],即
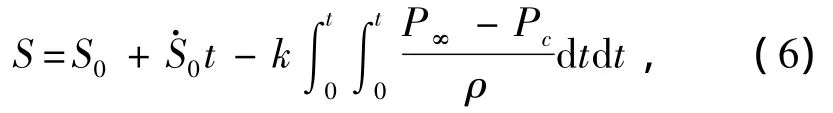
其中:
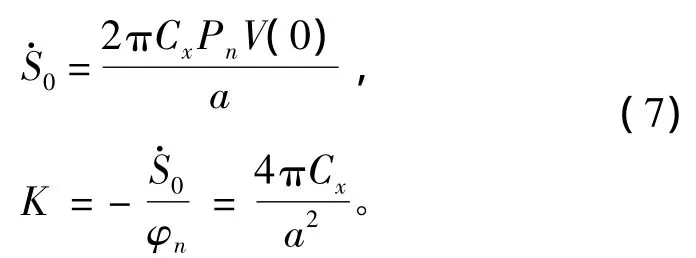
式中:S0为空泡截面的初始面积;p∞为无穷远处环境压力;pc为空泡内压力;Cx为阻力系数;Rn为空化器半径;V(0)为t=0时刻的空化器速度;a为常数,会略微受到空泡数的影响,通常的取值范围为1.5~2。
超空泡射弹在水中以高速 (接近跨音速甚至达到超音速)运动时,水的可压缩性成为空泡形态的重要影响因素之一[38-39]。超空泡射弹一般具有大长细比的特征。对此类细长形超空泡射弹,可以假定它引起的流场为小扰动,并采用细长体小扰动理论进行研究[40]。Serebryakov[41-43]和 Vasin[44-45]对该理论进行了详细的研究,并采用渐进法进行求解 (利用Riabushinsky闭合模型),并将计算结果与大量实验结果进行了对比,得到了超空泡射弹在可压缩流体中的空泡形态表达公式,一阶渐进解的表达式为[46]

式中:Rc为空泡半径;Rn为锥形体底面半径;l为锥形体长度;L=2l+Lc;x为空泡截面沿空泡长度方向距离锥形体顶点距离。
当空化器半径远小于空泡半径时,忽略空泡半径即可得空泡形态的二阶渐进解表达式[46],即

3.2 超空泡射弹受力分析
超空泡射弹在超空泡中运动受到的主要作用力有3部分:①超空泡射弹自身具有的重力;②超空泡射弹头部所受的阻力和升力;③超空泡射弹尾部与空泡壁撞击作用产生的撞击力 (在尾拍研究中将其定义为尾拍力)。
由于超空泡射弹在水中没有固定约束,在建立力矩方程时,一般将转动中心建立在质心位置,重力力矩为0,因此在尾拍分析中一般不考虑重力作用。
对于超空泡射弹头部所受的阻力和升力一般采用下式进行确定。
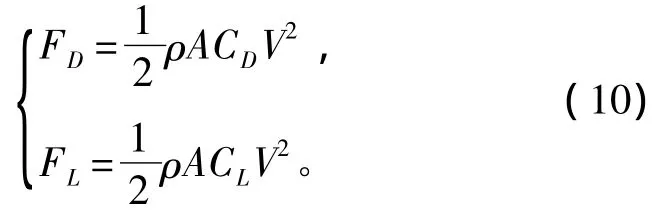
式中:A为空化器截面面积;V为射弹速度;CD和CL分别为阻力系数和升力系数[5]。
尾拍力的确定目前主要有2种方法,一种是基于动量守恒,利用Von Karman提出的虚拟质量法[47],求解出尾拍作用的升力RL、阻力RD,例如Rand[11],Ruzzene[14]和 Kulkarni[12]在处理尾拍作用力时利用该方法。另一种是根据势流理论求解出浸入水中固体边界受到压强,然后进行积分得到尾拍作用力RL,例如Kubenko[48]在分析航行体与空泡间隙对尾拍作用力的影响时利用该方法。
3.2.1 基于虚拟质量法的尾拍受力计算

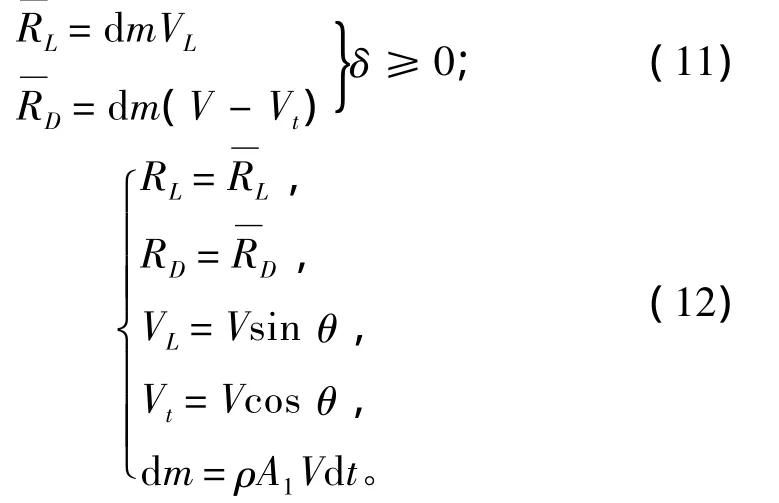
式中:A1=λδd为射弹尾部浸入液体边界层的特征面积;δ为射弹尾部侵入液体的深度。因此结构发生尾拍时所受阻力和升力可表达为式(13)。Ruzzene[14]采用的方法与 Rand[11]的方法类似,在此不再赘述。


图6 动量传递示意图Fig.6 Scheme of momentum transfer
Kulkarni[12]分析了射弹尾部浸入空泡壁的切片受力,并将切片受力对浸水长度lk积分得到尾拍作用力。假设射弹距尾部底面处在z1向速度Wξ,根据动量守恒可得
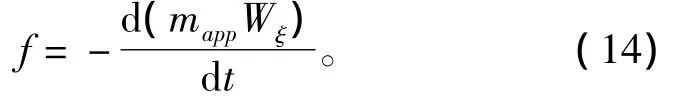
式中:mapp为射弹切片对应的虚拟质量,可表达为mapp=Kρdζ;K为常数,当射弹截面为圆时K=2π;d为射弹尾部直径;ζ为射弹切片浸入水深度(如图7所示)。射弹切片z1向速度Wξ可以表达为
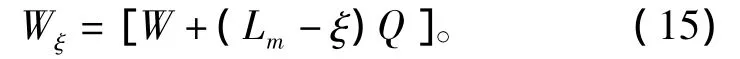
式中:W为射弹切片在z向速度;Lm为射弹长度;Q为射弹转动角速度。将式(15)代入式(14),并结合ζ·=Wξ和ζ=tan θ(lk-ζ),可得切片尾拍升力为

式中:

切片阻力与浸入水的截面积(如图7所示)有关,可分解为x1和z1两个方向的分力:
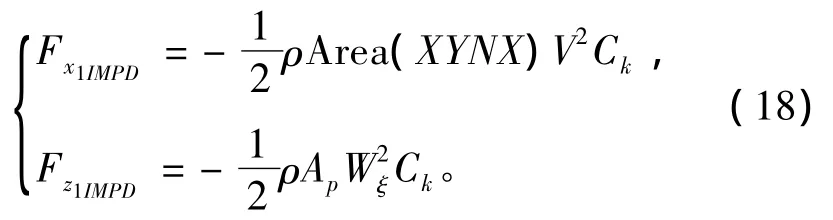
式中:Ck为阻力系数,取值范围为0.5~0.95;Area(XYNX)和Ap分别为射弹尾部切片浸入水在x1和z1方向的投影面积,表达为
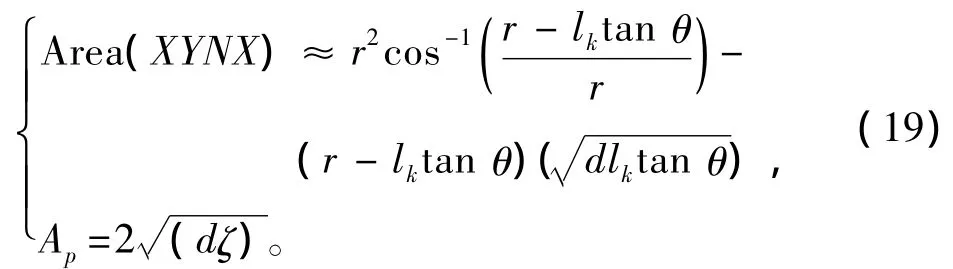
将式(19)代入式(18),可得:
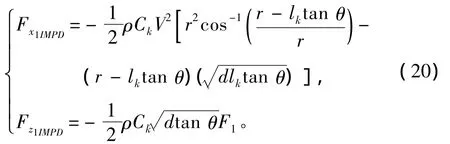
式中,
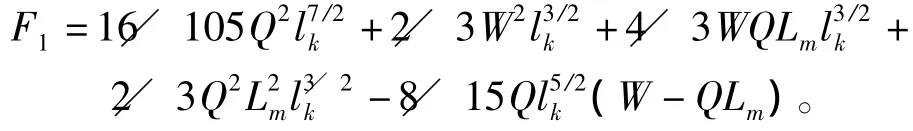
将式(18)及式(20)沿射弹尾部浸水长度lk积分即可得到尾拍作用力。

图7 超空泡射弹尾部切片浸入示意图Fig.7 Scheme of immersion of supercavitating projectile tail into water
3.2.2 基于势流理论的尾拍受力计算
Rand等人求解尾拍力所利用的方法虽然从形式上来说比较简单,但其过分简化了物体的受力情况。Kubenko[48]根据势流理论求解出浸入水中固体边界受到压强,然后进行积分得到尾拍作用力RL。该方法虽然较为复杂,但得出的超空泡射弹尾部撞击力更为完善。
当射弹与空泡壁面相互作用时,由于射弹与空泡都是细长体,可以对整个射弹浸入水的沾湿部分采用切片法处理。射弹尾部切片在浸入空泡壁内的流动问题都可以简化为圆柱体浸入圆柱形水面的平面出入水问题,可以应用切片法结算每个切片的平面受力。对于射弹尾部切面与空泡之间间隙为小间隙下,受力可表达为[19]
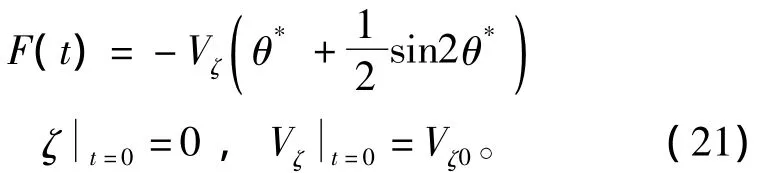
其中θ*如图8所示,可表达为

式中,Vζ为射弹切片入水速度;ζ为切片浸水最大深度;Δ为切片出空泡半径Rc与射弹切片半径r之间的间隙,表达为Δ=Rc-r。
将式(21)沿射弹尾部浸水长度lk积分即可得到尾拍作用力。

图8 超空泡射弹切片与空泡壁面接触示意图Fig.8 Scheme of impact of supercavitating projectile tail with cavity wall
3.3 超空泡射弹尾拍动力学模型建立
超空泡射弹在高速运动过程中的尾拍现象在涉及刚体运动的同时还会导致结构发生弹性振动,影响超空泡射弹的弹道以及结构的稳定性,因此超空泡射弹的运动是刚体运动与弹性振动的耦合问 题。 早 期 的 尾 拍 问 题 研 究 (如 Rand[11],Kulkarni[12]等)主要研究其刚体运动即弹道问题,但随着对尾拍研究的深入了解后,超空泡射弹尾拍涉及的结构振动问题越来越受到关注(如Ruzzene[14],Choi[15]等)。
以Ruzzene[14]文献为例,其建立的尾拍动力学方程为混合动力学方程。其文献中假设超空泡轴线不变,超空泡射弹绕空化器转动,且不计轴向伸缩形变,只考虑俯仰角θ和偏航角φ方向的挠度,利用哈密顿原理给出混合动力学方程的变分形式
式中:T为系统动能;U为系统弹性势能;W为外力做功。超空泡射弹分别受到头部流体阻力和升力(合力Fa沿轴向)以及尾部尾拍力F1,其中尾拍力表达形式为
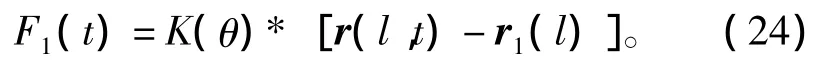
式中:K(θ)为俯仰角θ的函数;rI(l)为射弹尾部与空泡壁面接触的临界坐标。
图9给出超空泡射弹坐标系定义及变形示意图。定系O(x0,y0,z0),原点在超空泡射弹头部,空泡轴线坐落在x0轴上;动系为弹体坐标系Or(x,y,z)。当射弹做弹性运动时,泛点y方向挠度定义为v(x,t),z向挠度定义为w(x,t),泛点坐标可以定义为
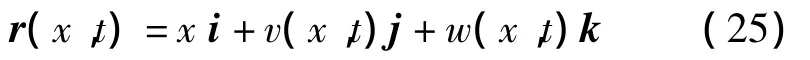
式(25)对时间t微分可得泛点速度
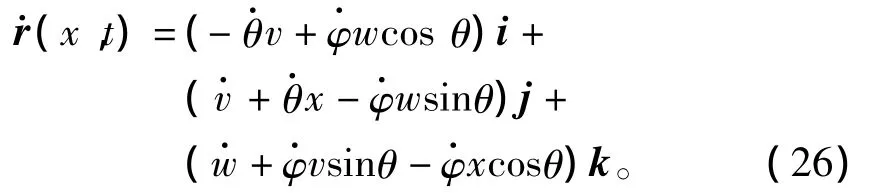
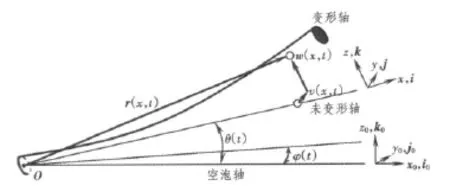
图9 坐标系定义及变形示意图Fig.9 Scheme of coordinate system and its deformation
由于超空泡射弹一般具有较大的长细比,将其考虑为欧拉-伯努利梁模型处理。当超空泡射弹发生弹性变形时,每个节点具有4个自由度分别描述y向和z向的位移和转角。因此,射弹单元位移定义为
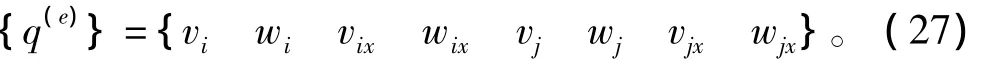
式中:i,j分别为单元的起点和终点编号;vx,wx分别为y向和z向转角。因此,射弹挠度可表达为
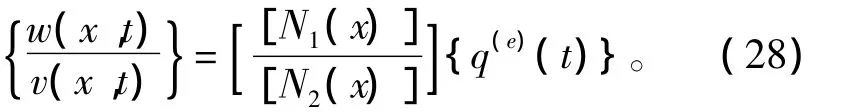
式中[N1(x)]和[N2(x)]为形函数。
动力学系统的动能T、弹性势能U和尾拍力做功WI分别为:
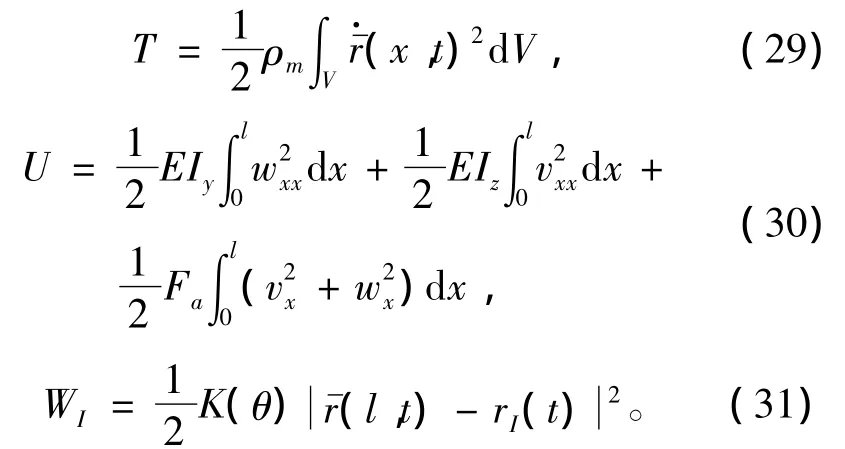
式中:ρm为射弹材料密度;E为弹性模量;Iy和Iz分别为y向和z向惯性矩;Fa为射弹头部受到的流体阻力。
将式(25)~式(28)代入式(29)~式(31),最终可得系统动力学微分方程有限元形式为
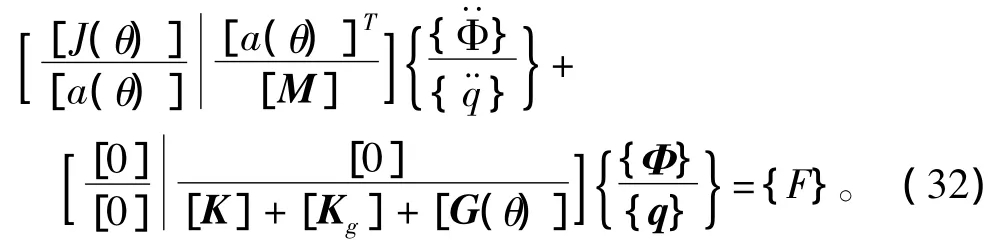
式中:[M],[K]和[Kg]分别为系统单元质量矩阵、单元刚度矩阵和几何刚度矩阵[49];[G(θ)]为与K(θ)相关的矩阵;{q}为射弹弹性位移矩阵;{Φ}={θ φ}T为射弹刚体运动自由度矩阵;{F}为广义力;[J(θ)]和[a(θ)]分别为射弹刚体转动惯量和耦合惯性距,可表示为
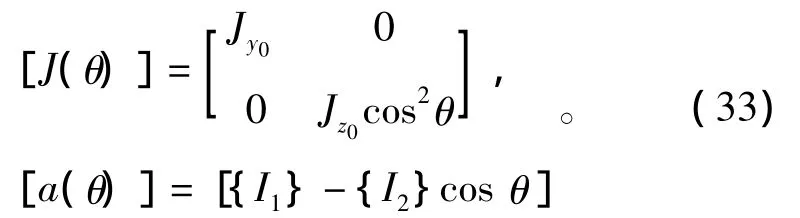
式中Jy0和Jz0分别为超空泡射弹绕头部的转动惯量。It表达为
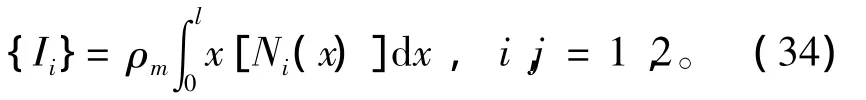
4 结语
高速超空泡射弹理论及数值分析技术尚未完善,有待于进一步发展。利用基于N-S求解、考虑空化、湍动和流体可压缩性的CFD方法,准确描述非定常、跨声速及超声速状态下的空泡形态以及高速射弹尾拍载荷等问题,是超空泡射弹尾拍流体动力学研究的努力方向。
随着流固耦合技术的不断发展,结构有限元将能够更好地和上述CFD技术结合进行耦合运算,建立更准确的超空泡射弹尾拍动力学模型,进一步发展超空泡射弹运动的流固耦合方法是超空泡射拍尾拍结构动力学研究的努力方向。
高速超空泡射弹自由飞行的实验对于超空泡射弹尾拍的研究也具有重要意义,目前实验研究受实验条件的限制较大,需要进一步提高实验测试能力,改进实验设备。超空泡射弹真实扰动的实验模拟,不同发射速度、不同扰动角速度以及射弹装配匹配等问题将是今后实验研究的主要方向。
[1]SAVCHENKO Y N.Supercavitation-problems and perspectives[A].CAV 2001.Fourth International Symposium on Cavitation[C].Pasadena:California Institute of Technology,2001.
[2]ASHLEY S.Warp-drive underwater[J].Scientific American,2001,284:62-71.
[3]于开平,隗喜斌,蒋增辉.俄罗斯和乌克兰超空泡减阻技术研究进展[J].飞航导弹,2007(8):5-11.
[4]KIRSCHNER I N.Results of selected experiments involving supercavitating flows[A].Supercavitating Flows[C].Hull:St.Joseph Ottawa,2002.PTO-EN-010-15.
[5]MAY A.Water entry and the cavity-running behavior of missiles[R].Arlington:Naval Sea Systems Command,1975.
[6]CASTANO J M,KUKLINSKI R.High-speed supercavitating underwater vehicle[P].United States:US6739266 B,May 25,2004.
[7]HARKINS T K,STEVES H K,GOELLER J E.Air-launched supercavitating water-entry projectile[P].United States:US5955698,Sep 21,1999.
[8]MISKELLY H L.Supercavitating underwater projectile[P].United States:US6405653 B1,Jun 18,2002.
[9]HARKINS T K,STEVES H K,GOELLER J E.Supercavitating water-entry projectile[P].United States:USH1938 H,Feb 6,2001.
[10]PRATAP R,RAND R.In-flight dynamics of high-speed underwater projectiles[R].AHSUM ProjectProgress Report,1996.
[11]RAND R,PRATAP R,RAMANI D,et al.Impact Dynamics of a supercavitating underwater projectile[A].Proceeding of the 1997 ASME Design Engineering Technical Conferences[C].Sacramento,California,1997.
[12]KULKARNI S S,PRATAP R.Studies on the dynamics of a supercavitating projectile[J].Applied Mathematical Modelling,2000,24(2):113-129.
[13]MILWITZKY B.Generalized theory for seaplane impact[R].Washington:NACA-TR-1103,1952.
[14]RUZZENE M,SORANNA F.Impact dynamics of elastic supercavitating underwater vehicles[A].9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization[C].Atlanta,Georgia,2002.AIAA 2002-5632.
[15]CHOI J Y,RUZZENE M,BAUCHAU O A.Dynamic analysis offlexible supercavitating vehicles using modal-based elements[J].Simulation,2004,80:619-633.
[16]ABE A,KATAYAMA M,SAITO T,et al.Numerical simulation on supercavitation and yawing of a supersonic projectile traveling in water[A].Symposium on Interdisciplinary Shock Wave Research[C].Sendai,Japan,2004.
[17]PUTILIN S I.Some features of a supercavitating model dynamics[J].International Journal of Fluid Mechanics Research,2001,28(5):631-643.
[18]PUTILIN S I.Stability of supercavitating slender body during water entry and underwater motion[A].High Speed Body Motion in Water[C].Hull:Canada Communication Group Inc,1998.AGAROR-827-27.
[19]KUBENKO V D.Impact of a long thin body on a cylindrical cavity in liquid:a plane problem[J].International Applied Mechanics,2006,42(6):32-53.
[20]ZIRAKSAZ M H.Solid propellant application in high speed underwater projectiles and bullets[A].44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit[C].Hartford,July 2008.CT:AIAA-2008-4975.
[21]KIRSCHNER I N.Results of selected experiments involving supercavitating flows[A].Supercavitating Flows[C].Hull:St.Joseph Ottawa,2002.RTO-EN-010-15.
[22]KIRSCHNER I N,ROSENTHAL B J,UHLMAN J S.Simplified dynamical systems analysis of supercavitating highspeed bodies[A].Fifth International Symposium on Cavitation[C].Osaka,Japan,2003.CAV03-OS-7-005.
[23]HRUBES J D.High-speed imaging of supercavitating underwater projectiles[J].Experiments in Fluids,2001,30:57-64.
[24]VLASENKO Y D.Experimental investigation of supercavitation flow regimes at subsonic and transonic speeds[A].Fifth International Symposium on Cavitation[C].Osaka,Japan,2003.CAV03-GS-6-006.
[25]LOGVINOVICH G V.Some problems of supercavitating flows[A].High speed body motion in water[C].Hull:Canada Communication Group Inc,1998.AGARDR-827-18.
[26]孟庆昌,张志宏,顾建农,等.超空泡射弹尾拍分析与计算[J].爆炸与冲击,2009,29(1):56-60.MENG Qing-chang,ZHANG Zhi-hong,GU Jian-nong,et al.Analysis and calculation for tail-slaps of supercavitating projectiles[J].Explosion and Shock Waves,2009,29(1):56-60.
[27]潘展程,鲁传敬,李杰,等.超空泡航行体做受迫纵荡运动的数值模拟[A].第21届全国水动力学研讨会暨第八届全国水动力学学术会议暨两岸船舶与海洋工程水动力学研讨会文集[C].北京:海洋出版社,2008.749-755.
[28]张鹏,傅慧萍.跨超音速射弹的超空泡数值模拟[J].弹箭与制导学报,2009,29(5):166-169.ZHANG Peng,FU Hui-ping.The numerical simulation of supercavitation around projectiles from subsonic to supersonic[J].Journal of Projectiles,Rockets,Missiles and Guidance,2009,29(5):166-169.
[29]杨传武,刘刚,王安稳.超空泡体结构响应问题的有限元分析[J].海军工程大学学报,2008,20(2):101-104.YANG Chuan-wu,LIU Gang,WANG An-wen.FEM analysis of structural response of supercavitating bodies[J].Journal of Naval University of Engineering,2008,20(2):101-104.
[30]杨传武,王安稳.冲击载荷作用下超空泡水下航行体的结构响应[J].华中科技大学学报(自然科学版),2008,36(7):129-132.YANG Chuan-wu,WANG An-wen.Structural response of supercavitating underwater vehicles subjected to impact loads[J].JournalofHuazhong University ofScience and Technology(Nature Science Edition),2008,36(7):129-132.
[31]张劲生,张嘉钟,魏英杰,等.超空泡水下航行体的结构动力响应特性[J].北京航空航天大学学报,2010,36(4):411-414.
[32]ZHANG J Z,ZHANG J S,WEI Y J.Simulation of tail-slap loadsofsupercavitating projectiles[A].The Third International Conference on Information and Computing Science[C].Wuxi,China,2010.
[33]HE Q K,ZHANG J Z,WEI Y J,et al.Dynamic response of supercavitating underwater vehicle impacted by tail-slap force[J].Applied Mechanics and Materials,2011(50-51):536-540.
[34]曹伟,王聪,魏英杰,等.自然超空泡形态特性的射弹试验研究[J].工程力学,2006,23(12):175-187.
[35]SEMENENKO V N.Computer simulation of unsteady supercavitating flows[A].High Speed Body Motion in Water[C].Hull:Canada Communication Group Inc,1998.AGARD-827-22
[36]LOGVINOVICH G V.Hydrodynamics of flows with free boundaries[M].Kiev:Naukova Dumka,1969.
[37]VASIN A D.The principle of independence of the cavity sections expansion asthe basisforinvestigation on cavitation flows[A].Supercavitating Flows[C].Hull:St.Joseph Ottawa,2002.RTO-EN-010-8.
[38]LOGVINOVICH G V.Subsonic compressible flow past a body with developed cavitation[J].Fluid Dynamics,2002,37(6):873-876.
[39]YAKIMOV Y L.Thin cavitation cavity in a compressible fluid[A].Problems of Contemporary Mechanics,Part I[C].Moscow:Moscow University Press,1983.63-73.
[40]YAKIMOV Y L.Asymptotic laws of degeneration of thin cavity shapes[J].Izv Akad Nauk SSSR Mekh Zhidk Gaza,1981,(3):3-10.
[41]SEREBRYAKOV V V.Problems of hydrodynamics for high speed motion in water with supercavitation[A].Sixth International Symposium on Cavitation[C].Wageningen,Netherlands,2006.CAV2006-134.
[42]SEREBRYAKOV V V.Asymptotic solutions of problems of axisymmetrical supercavitation flow in slender body approximation[A].High Speeds Hydrodynamics[C].Cheboksary:Chuvash University Press,1990.99-111.
[43]SEREBRYAKOV V V.Asymptotic solutions of axisymmetrical problems of subsonic and supersonic separated water flows with zero cavitation numbers[J].Dokl Akad Nauk Ukraine,1992(9):66-71.
[44]VASIN A D.Thin axisymmetric cavities in subsonic compressible flow[J].Izv Akad Nauk SSSR Mekh Zhidk Gaza,1987(5):174-177.
[45]VASIN A D.Thin axisymmetric cavities in supersonic flow[J].Izv Akad Nauk SSSR Mekh Zhidk Gaza,1989(1):179-181.
[46]VASIN A D.Supercavities in compressible fluid[A].Supercavitating Flows[C].Hull:St.Joseph Ottawa,2002.RTO-EN-010-16.
[47]KARMAN T V.The impact of seaplane floats during landing[R].Washington:NACA-TN-321,1929.
[48]KUBENKO V D,GAVRILENKO O V.Impact interaction of cylindrical body with a surface of cavity during supercavitation motion in compressible fluid[J].Journal of Fluids and Structures,2009,25(5):794-814.
[49]PAZ M.Structural dynamics:theory and computation[M].NewYork:Van Nostrand-Reinhold,1985.
