微电网中双馈感应风力发电系统控制方法研究

李国庆，王 鹤，2，李鸿鹏

（1.东北电力大学 电气工程学院，吉林 吉林 132012；2.华北电力大学 电气与电子工程学院，北京 102206）

0 引言

风能是一种分布广泛的清洁能源，随着风电设备成本的降低和可靠性的提高，风力发电可以作为微电网中优先选择的分布式电源[1-3]。微电网是较薄弱的小型发配电网络，风力发电的接入会对微电网的稳定运行造成影响，风速的随机变化会导致风电功率的明显波动和电能质量的下降[4-6]。采用双馈感应发电机 DFIG（Doubly Fed Induction Generator）的变速恒频发电机组是当前风力发电的主流机型，所以对微电网中DFIG发电系统控制方法的研究具有重要的意义[7-8]。文献[9] 利用DFIG对微电网的频率和电压进行管理，提高了微电网从并网向孤岛运行方式过渡过程中的动态性能。文献[10] 提出了一种将由DFIG组成的风电场并入微电网的控制方法，特别适合以风力发电作为主要电源的微电网使用。文献[11] 提出了一种基于DFIG的无功功率管理方法，能够有效地维持系统的电压稳定。

微电网的并网和孤岛2种运行方式存在很大区别，本文针对微电网的并网及孤岛运行状态，分别提出了相应的DFIG风力发电系统控制方法。微电网并网运行时DFIG捕获最大风能，并且计及微电网线路中电阻参数所占比重较大导致风功率变化引起的电压波动，采用灵敏度分析的方法根据有功功率变化调整输出的无功功率来稳定微电网的电压。微电网孤岛运行时，DFIG采用变桨距角控制并结合储能装置限制风电功率，使DFIG以频率和电压可控的方式工作，通过模拟下垂特性与其他逆变器电源一起协调控制微电网的频率和电压。仿真实验结果表明本文提出的微电网中DFIG风力发电系统控制方法能够有效地解决风力发电向微电网中的集成。

1 微电网结构与组成

本文选择DFIG风力发电、微型燃气轮机、燃料电池和光伏发电作为分布式电源，使用蓄电池作为储能装置，并结合负荷、电力电子接口设备和相应的控制装置构成微电网的主体结构，如图1所示。在整体控制策略上，本文采用微电网的分层控制结构[12]。微电网中心控制器MGCC（MicroGrid Central Controller）和负荷控制器 LC（Load Controller）、微电源控制器MC（Microsource Controller）之间需要建立可靠的通信连接。MGCC安装在中压-低压变电站对微电网进行统一的协调控制；LC和MC从属于MGCC，分别对具体的负荷和微电源进行控制。

图1 微电网结构Fig.1 Structure of microgrid

微型燃气轮机能够提供25～500 kW的稳定功率输出，具有高燃料利用效率、低废气排放水平、低初始安装费用等优点。本文选择高速单轴结构的微型燃气轮机 SSMT（Single-Shaft MicroTurbine），使用文献[13] 中给出的动态数学模型。单轴微型燃气轮机可以直接驱动永磁同步电机发电，发出的高频交流电经过整流和逆变之后向电网或者负荷供电。固体氧化物燃料电池SOFC（Solid Oxide Fuel Cell）是一种在中高温下直接将燃料中的化学能转化成电能的新型发电装置，属于第3代燃料电池技术，具有燃料适应性广、能量转换效率高、零污染、低噪声等优点。本文采用文献[14] 中的数学模型，并在SOFC电池组输出端接入Buck-Boost直流变换电路，最终通过逆变器将Buck-Boost电路输出的直流电压逆变成交流电压向电网或者负荷供电。光伏发电是另一种具有广泛应用前景的分布式电源，具有可再生、无污染、方便灵活、可与建筑集成等优点。本文采用文献[15] 中的光伏发电模型，使用扰动观察法来进行最大功率点跟踪，在给定的温度和光照条件下，保证光伏发电系统一直运行在最大功率点附近。此外，本文选择蓄电池作为储能装置，并采用文献[16] 中的三阶动态数学模型，其较精确地反映了蓄电池的充放电特性。

2 微电网中DFIG风力发电系统控制方法

2.1 DFIG数学模型

本文采用计及定子励磁电流变化的DFIG数学模型来研究其在微电网不同运行状态下的控制方法。在同步旋转坐标系下，DFIG的电压和磁链方程如下[17]：

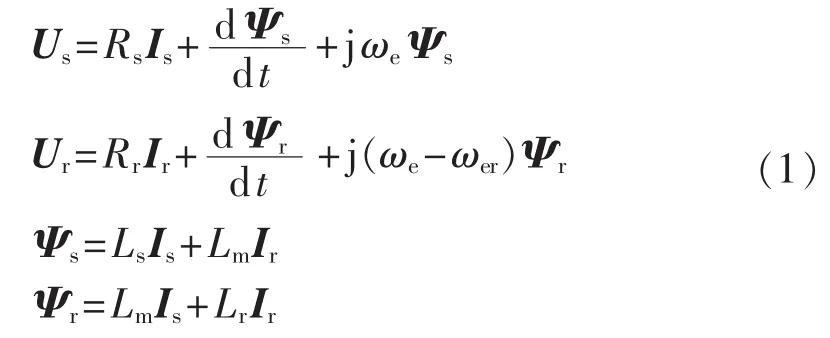
其中，Us、Ur、Is、Ir、Ψs、Ψr分别是定子和转子电压、电流和磁链矢量；Rs、Rr、Ls、Lr分别是定子和转子电阻和绕组自感；Lm是定子和转子之间的互感；ωe是同步电角速度；ωer是转子电角速度。

计及定子励磁电流变化，令Imo=LsIs／Lm+Ir，则有下述DFIG数学模型：

其中，定子和转子间漏磁系数 σ=1-L2m／（LrLs），转差电角速度ω1=ωe-ωer。

2.2 微电网并网运行时DFIG控制方法

为了减小风速波动对微电网的影响，本文在DFIG出口处并联了由超级电容和蓄电池组成的混合储能装置。微电网并网运行时，DFIG风力发电系统的控制原理如图2所示，控制方法由转子变流器控制、最大功率点跟踪、网侧变流器控制、储能系统控制和功率协调控制组成。

图2 微电网并网运行时DFIG控制Fig.2 DFIG control of grid-connected microgrid

DFIG转子变流器控制采用定子磁链定向的矢量控制方法，并且计及定子励磁电流的变化，在较精确的模型下实现了有功功率和无功功率的解耦控制。对转子变流器，考虑Us和Ψs的动态过程，由式（2）可得：

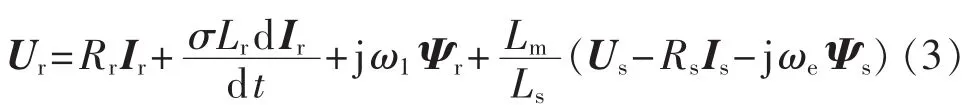
选择定子磁链定向，下标d、q分别表示各变量的d轴和q轴分量。在dq坐标下，有，式（3）可以写成：

可以根据式（4）对DFIG的有功功率和无功功率进行解耦控制，定子有功功率和无功功率控制闭环产生转子q轴和d轴参考电流I*rq和I*rd，具体的控制原理可参考文献[18] 。转子变流器有功功率参考值Pr*由最大功率点跟踪方法给出，无功功率参考值Qr*由功率协调控制给出。

为了提高微电网并网运行时的风能利用效率，需要进行最大功率点跟踪。假设风速为v，则风轮机能够捕获的最大功率可以表示为：

其中，ρ是空气密度；S是风轮扫风面积，在最大功率点跟踪算法中都可以看成常数；Cp（λ，β）是风能利用系数，其是叶尖速比λ和桨距角β的函数，文中将其简写为Cp，Pw只与Cp有关。本文利用DFIG输出总功率的单峰特性，采用搜索的方法实现最大功率点跟踪[19]。

网侧变流器控制采用电网电压定向的矢量控制方法，如果网侧变流器通过一个变压器与交流电网相连，则：

其中，Ugd是电网电压Ug的d轴分量；Igd、Igq分别是电网电流Ig的d轴、q轴分量；R和L分别是变压器的等效电阻和电感；ed、eq分别是变流器输入控制电压的d轴和q轴分量。由于采用电网电压定向Ugd=0，Igd和Igq分别代表了变流器的有功电流分量和无功电流分量，可以实现功率的解耦控制。其d轴参考电流I*gd由直流电压Udc控制闭环产生，为转子变流器提供稳定的直流电压，q轴参考电流Ig*q由无功功率Qg控制闭环产生，其参考值Q*g由功率协调控制给出。

混合储能装置中逆变器和双向DC-DC变换器的控制方法参考文献[20] ，逆变器采用电网电压定向的矢量控制方法实现有功功率和无功功率的解耦控制。储能装置的有功功率和无功功率参考值PC*、QC*均由功率协调控制给出。微电网并网正常运行时，由大电网帮助维持功率平衡，储能装置有功功率设定值PC*=0。

微电网线路的电阻参数较大，风力发电有功功率的随机变化将会导致电压的明显波动。本文中的功率协调控制采用灵敏度分析的方法，根据捕获的最大功率Pr*调节DFIG风力发电系统所发出的无功功率Q来稳定电压，并将无功功率在定子侧（转子变流器控制）、网侧变流器和储能装置之间分配。

首先确定Q值，考虑并网接口节点处的潮流方程，在运行点处将潮流方程线性化：

其中，P是DFIG风力发电系统所发出的有功功率，U、θ分别是并网接口处电压的幅值和相角。假设潮流方程的雅可比矩阵是非奇异的，则灵敏度矩阵方程为：

其中，SθP、SθQ、SUP、SUQ均是灵敏度矩阵中的元素，下标中的2个字母代表灵敏度关联的2个量。由上式可得由DFIG有功功率和无功功率变化引起的并网接口处的电压偏移：

为了调节微电网侧并网接口处电压与大电网侧电压近似一致，DFIG风力发电系统应该发出的无功功率为：

其中，P0、Q0分别是运行点处的有功功率和无功功率，ΔU0是运行点处电压与微电网并网电压之间的差值。

由网侧变流器优先承担系统要发出或吸收的无功功率。当网侧变流器能力不足时，由定子侧补充，这一优先顺序考虑了定子侧发出无功功率时定子电流增加所造成的损耗。当DFIG本身发出或吸收的无功功率不能满足电压管理要求时，由储能装置提供支持。

2.3 微电网孤岛运行时DFIG控制方法

当微电网孤岛运行时，与大电网的连接断开。为了维持微电网的稳定运行，需要对DFIG的输出功率进行限制。此时，DFIG风力发电系统的控制原理如图3所示，控制方法由转子变流器控制、桨距角控制、网侧变流器控制、储能系统控制和功率协调控制组成。其中网侧变流器控制和储能系统控制采用的方法与微电网并网运行时相同，不再介绍。转子变流器仍然采用定子磁链定向的矢量控制方法，但是定子磁链Ψs不再由定子侧电压Us决定，而是受励磁电流幅值Imo控制。Ψs的相位角θs不再通过观测Us得到，而是通过对定子电压频率参考值f*s的积分得到。DFIG不再捕捉最大风功率，而是表现为一个电压和频率可控的交流电源[21]。

图3 微电网孤岛运行时DFIG控制Fig.3 DFIG control of islanded microgrid

从上式可以看出，在dq坐标系下，定子磁链可以通过励磁电流Imo控制，并且为了实现定子磁链定向，Irq需要根据Isq进行调整，故选择参考值如下：

其中，fs是DFIG定子侧电压频率，U*s是定子侧电压幅值的参考值。

由式（2），考虑Ψsq=0，可以将定子侧电压方程简化为：

令定子时间常数 τms=Ls／Rs，定子漏磁系数σs=（Ls-Lm）／Lm，有：

由上式，考虑到微电网稳定运行时Us变化较小，Imo可以通过定子d轴电流Isd控制。

由式（11）—（14），通过上述定子磁链定向的矢量控制方法，DFIG可以看作是一个频率和电压可控的交流电源。该方法最大的缺点是不能够直接控制DFIG的转矩，因为Isq由负载决定，Irq必须跟踪Isq的变化而不能用来控制转矩。

本文采用桨距角控制来间接控制DFIG的转矩，式（5）中风能利用系数由下式确定：

其中，N是齿轮比，ωr是轴角速度。则桨距角控制的参考值为：

其中，Pn是设定的负荷有功功率需求，C*p、λ*、β*、ω*r分别是各变量的参考值。将上式线性化，用下标0表示线性化的点，符号δ表示变量在线性化点附近的微小增量，得到：

DFIG的转矩和转速由下式决定：

其中，Tm和Te分别是DFIG的机械转矩和电磁转矩，J是转动惯量。同样将上式线性化，有：

进一步整理，得：

其中，M1—M8、N1—N3是计算的中间变量。设 τβ是桨距角变化的时间常数，则桨距角的动态变化满足如下关系：

由桨距角和转速构成状态变量，由式（21）和式（23）可以得出状态方程为：

式（24）中状态变量、输入变量和扰动分别为：

系数矩阵分别为：

桨距角控制的最大调节速度受机械调整部件的限制，本文中限制最大调节速度为±3°／s，所以桨距角控制需要具有良好的阻尼。经过反复实验验证，本文选择闭环极点为-0.15和-1.5，此时系统为过阻尼状态，阻尼比为1.7。该闭环极点设置能够同时满足限制最大调节速度和较快速响应的要求。根据闭环极点的设置方法，此时相应的反馈系数为kf1=0.65，kf2=-0.88。综合上述分析，桨距角控制的输入信号由下式产生：

DFIG的功率协调控制负责配合桨距角控制维持DFIG的功率平衡。当可用风功率Pw＜Pn时，不进行桨距角调整，使β=0，功率协调控制设定储能系统来补充风功率的不足。当Pw＞Pn时，由风功率提供全部Pn，并且优先通过桨距角控制调整DFIG输出的有功功率。由于桨距角控制响应较慢，当调节能力不足时，由储能装置配合调节。本文通过设定桨距角控制中转子角速度ωr的上、下限ωrh和ωrl与储能装置协调，即令：

当风速增加，桨距角控制不满足要求，转子角速度ωr＞ωrh时，功率协调控制通过设定储能系统的PC*来吸收额外的功率；当风速降低，转子速度ωr＜ωrl时，功率协调控制设定PC*来补充不足的功率需求。在孤岛运行时，本文选择储能系统优先发出或吸收无功功率。

微电网孤岛运行时，DFIG的有功功率和无功功率需求Pn和Qn由下垂特性给出。本文中DFIG采取可变的下垂系数，当风速变化较大时，可以通过改变下垂系数来修改Pn，既降低了储能装置的充放电次数，又避免了风电功率与需求功率差额较大时储能装置的能力不足。

可变下垂系数由预先设定好的几组不连续下垂系数组成。每组中所有分布式电源的下垂系数之和相等，这样能够保证微电网频率和电压的单位调节功率是固定的，下垂系数调整的结果是使负荷在各个分布式电源中重新分配。在其他分布式电源容量允许的情况下，几组下垂系数按照DFIG承担的负荷比例从大到小顺序排列。设定DFIG可用风电功率Pw和需求功率Pn之间差额的阈值，当Pw-Pn＜0时，将下垂系数调整为后一组，减少DFIG承担的负荷比例，即减少 Pn和 Qn；反之，当 Pw-Pn＞0.2 p.u.时，将下垂系数调整为前一组，增加Pn和Qn。

因为风功率具有随机性，下垂系数的修改不能是连续实时的，否则会因下垂系数的频繁变化影响系统的稳定运行。可以设定每间隔一段时间检测一次，如果调整的阈值条件满足并保持2 s，则对下垂系数进行调整。

3 仿真分析

本文采用PSCAD／EMTDC仿真软件搭建了微电网仿真实验平台。本文共有2个算例，采用图1中的微电网结构，DFIG、微型燃气轮机、燃料电池、光伏发电和蓄电池5条线路都是380 V线路，参数为R1=0.641ω ／km，X1=0.101ω ／km，5 条线路长度分别为200 m、400 m、200 m、200 m和20 m。大电网侧线路为10 kV线路，参数为 R2=0.347ω ／km，X2=0.2345ω ／km，线路长度为 1000 m。此外，DFIG、微型燃气轮机、燃料电池和光伏发电的主要参数详见参考文献[13-17] 。

算例1：微电网并网运行，微型燃气轮机、燃料电池和光伏发电都采用PQ控制，DFIG跟踪最大风功率，仿真实验结果见图4。

图4（a）中转速、直流侧电压及转矩为标幺值。从图中可看出，仿真实验采用的风速在10～12.5 m／s之间变化。通过最大风功率跟踪，DFIG转速随风速变化。当风速变化较慢时，转速的实际值与控制的设定值基本保持一致；当风速发生突变时，转速的实际值会短时偏离设定值，并逐渐跟踪设定值的变化。在整个仿真实验过程中，DFIG直流侧电压保持稳定，DFIG的电磁转矩Te和机械转矩Tm保持平衡，与捕获的风功率变化相一致。

图4 微电网并网运行DFIG仿真结果Fig.4 Simulative results of DFIG control for grid-connected microgrid

图4（b）中纵轴均为标幺值，前2幅图分别给出了采用单位功率因数控制和采用灵敏度分析方法控制无功功率时DFIG的功率仿真实验结果。2种情况下DFIG的有功功率P相同，都捕获了最大的风能。单位功率因数控制时DFIG不发出无功功率，Q=0，采用灵敏度分析方法控制时发出的无功功率Q随有功功率P变化而不断调整。第3幅图中Qg和Qs分别表示采用灵敏度分析方法时网侧变流器和定子侧发出的无功功率，从图中可以看出Q优先由网侧变流器承担，当网侧变流器能力不足时才由定子侧负责承担。第4幅图给出了2种情况下并网接口处节点电压的比较，可以看出采用单位功率因数控制时电压Urms1受DFIG有功功率变化的影响有明显的波动，而采用灵敏度分析方法控制DFIG的无功功率后电压Urms2得到改善。

算例2：微电网孤岛运行，光伏发电采用PQ控制，跟踪最大功率约16 kW，微型燃气轮机、燃料电池和DFIG都模拟下垂特性，仿真开始时微型燃气轮机和燃料电池下垂系数选择为kP1=100 kW／Hz、kQ1=1.31579 kvar／V，运行点为 40 kW、380 V，DFIG 下垂系数选择为 kP2=200 kW／Hz、kQ2=1.31579 kvar／V，运行点为80 kW、380 V。可变下垂系数采用较简单的情况，只在10 s时刻进行一次检测，并且只采用2组下垂系数。除初始下垂系数之外，另一组下垂系数设置为 kP1=150 kW ／Hz、kQ1=1.315 79 kvar／V ，kP2=100 kW／Hz、kQ2=1.315 79 kvar／V。负荷参数为 P1=45 kW，Q1=8 kvar，P2=55 kW，Q2=6 kvar，P3=40 kW，Q3=6 kvar，在10 s时刻有功负荷突然增至P1=85 kW，P2=85 kW，P3=90 kW，在20 s时刻，有功负荷突然增加到P1=120 kW，P2=125 kW，P3=95 kW。采用恒定下垂系数和可变下垂系数2种情况下的仿真实验结果如图5所示。

图5（a）中可用风功率为标幺值，由图可见仿真实验使用的风速与算例1相同。从图中可以看出，可用的最大风功率随风速不断变化，而且2种情况下系统的频率变化基本相同。这是因为下垂系数的调整中保证微电网频率和电压的单位调节功率不变，虽然下垂系数发生了变化，但整体上相同的功率变化引起的频率变化相同，只是负荷在分布式电源之间进行了重新分配。

图5 微电网孤岛运行DFIG仿真结果Fig.5 Simulative results of DFIG control for islanded microgrid

图5（b）中纵轴均为标幺值，前2幅图分别给出了2种情况下DFIG的有功功率设定值Pn和实际值Pw。第1幅图采用恒定下垂系数时DFIG有功功率不能满足下垂控制给出的设定值，第2幅图在可变下垂系数情况下，DFIG基本可以承担全部由下垂控制给出的有功功率设定值。后2幅图分别是储能装置在2种情况下的有功功率和无功功率对比，下标1表示恒定下垂系数，下标2表示可变下垂系数。从图中可以看出，无功功率下垂系数在调整时保持不变，所以2种情况下DFIG的无功功率基本相同。下垂系数控制模块在10 s时刻检测到Pw-Pn＜0，并保持2 s，满足调整条件，将下垂系数调整为后一组。此时，kP2由 200 kW ／Hz 变为 100 kW ／Hz，Pn由 0.6 p.u.变成0.4 p.u.。原本DFIG风功率无法满足负荷功率需求，调整后能够满足。从后2幅图中可以看出，恒定下垂系数时需要储能装置不断配合平衡风功率的变化，而采用可变下垂系数时通过改变Pn使负荷的需求主要由风功率提供，避免了储能装置的频繁动作和能力不足。

图5（c）是2种情况下DFIG转速和桨距角的变化情况，桨距角控制的最大调节速度为±3°／s，图中转速为标幺值。从图中可以看出，采用可变下垂系数时DFIG的转速和桨距角变化比恒定下垂系数时平缓得多，避免了短期的快速反复调节。

4 结论

本文提出了一种微电网中DFIG风力发电系统的控制方法，该方法充分考虑了微电网2种运行方式的特点。并网运行时通过最大功率跟踪充分利用风能，并且利用灵敏度分析方法稳定风功率变化引起的电压波动；孤岛运行时模仿下垂特性与其他分布式电源一起协调控制微电网的频率和电压，通过同步设置可变的下垂系数调整DFIG的有功需求，并通过桨距角控制和储能装置的支持调节DFIG的有功功率输出。仿真实验结果表明本文提出的方法能够有效克服风速变化对微电网稳定运行的影响，实现风能的高效可靠利用。