含有风电与光伏发电以及电动汽车的电力系统概率潮流

吴晨曦，文福拴，陈 勇，辛建波

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.杭州电子科技大学 自动化学院，浙江 杭州 310018；3.杭州市余杭供电局，浙江 杭州 311100；4.江西省电力科学研究院，江西 南昌 330006）

0 引言

概率潮流PLF（Probabilistic Load Flow）计算的概念是在20世纪70年代提出的[1]，其能够综合考虑各种随机因素，应用概率理论来描述电力系统稳态运行特性。概率潮流已经在电力系统分析的许多方面得到成功应用，如网损分析、可靠性评估、可用输电能力概率分析、暂态稳定分析等。通过概率潮流可以得到线路过负荷、母线过电压等的概率统计量，对发现和解决电力系统的潜在问题与薄弱环节具有重要作用。

随着化石能源的逐步枯竭和温室气体导致的全球变暖问题的趋于严重，风力发电与光伏发电等可再生能源发电得到了快速发展[2-3]。风力发电和光伏发电具有间歇性，二者同时也具有一定的互补性。长期来看，某些季节风能丰富但光能较少，而有些季节风能较少而光能丰富；短期来看，白天光能丰富，夜晚基本没有光能但一般风能较大。风光互补系统能够在一定程度上弥补单独风力发电或光伏发电的供电不稳定性。文献[4] 用修正的RBTS（Roy Billinton Test System）和IEEE-RTS构建了4个测试系统，研究了风电渗透率为14%～15%时的系统供电可靠性。文献[5] 用滑铁卢大学仿真实验室（WATSUN）开发的光伏发电系统仿真软件WATSUN-PV仿真每小时的太阳辐射强度，用风速历史数据预测下一小时的风速，对不同渗透率和不同位置情况下风能与太阳能对系统供电可靠性的影响与燃料节省情况进行了研究。文献[6] 采用多目标遗传算法优化风电、光伏发电和柴油机组成的混合系统结构和控制策略，分别以孤岛系统使用年限内的费用最小和失负荷最少为目标，确定Pareto前沿。文献[7] 以年费用最小为目标优化风机数量、轮毂高度、光伏电池板的倾角和配套的蓄电池容量，并已应用于我国东部沿海一带的通信中继站供电方案设计。

近年来，电动汽车（EV）在很多国家尤其是发达国家得到了快速发展，成为今后一段时间内有望明显拉动电力负荷上升的一个重要行业。现有的研究工作表明绝大多数电动汽车在一天中的96%的时间里是闲置的[8]。通过电动汽车接入网络V2G（Vehicle to Grid）技术[9]，这些闲置的电动汽车可以在用电高峰期将电能反送到电力系统中。所以，可入网电动汽车PEV（Plug-in Electric Vehicle）也可以被当作储能装置使用。另一方面，大量电动汽车广泛接入会给电力系统的安全与经济运行带来显著的不确定性。

概率潮流可用于研究风电和光伏发电出力以及电动汽车消耗功率和向电力系统反向供电功率的不确定性对电力系统的影响，发现系统运行中的潜在风险，为系统运行控制提供参考。已有一些针对包括风电、光伏发电和电动汽车的电力系统概率潮流计算方面的研究报道。文献[10] 考虑风力发电机出力与电动汽车供需随机性，以多控制变量约束为目标的最优潮流，采用混合自动学习机系统HLAS（Hybrid Learning Automata System）对多目标约束控制变量进行优化。文献[11] 假设负荷服从正态分布、风速服从Weibull分布，建立了相应的概率潮流模型。文献[12] 则采用蒙特卡洛（MC）仿真方法求解含有光伏发电的配电系统概率潮流。

到目前为止，尚没有针对含有风力与光伏发电和电动汽车的电力系统进行概率潮流计算的研究报道。且在现有的研究工作中一般都用Weibull分布来模拟风速变化，用当地纬度、太阳赤纬、日出日落时角等参数计算太阳辐射强度，没有考虑风速和光照的季节特性与实际天气状况及一天中各小时的特性。事实上，每天的实际日照时数是决定太阳辐射量的最主要参数之一。这里采用三点估计法（3PEM）进行概率潮流计算，旨在以较少的计算量获得与大量蒙特卡洛仿真计算同等精度的结果[13-14]。

在上述背景下，本文对含有风力与光伏发电和电动汽车的电力系统的概率潮流计算问题进行研究。首先推导一天内每个小时的风电机组出力与光伏发电出力的概率密度，并建立一天各时段电动汽车的充放电概率密度；然后发展了考虑天气状况的三点估计法概率潮流求解方法；最后，用真实的气象日值数据模拟不同季节的每天日照时数与日平均风速，并以某140节点配电系统为例来说明所构造的概率潮流模型的基本特征。本文所发展的概率潮流模型既考虑了风电和光伏发电的季节特性，又计及了风电和光伏发电的短期输出功率和电动汽车充／放电功率的不确定性，可以更准确地模拟系统运行状况。

1 风电／光伏发电出力的概率密度与电动汽车充／放电功率概率密度

1.1 风电机组出力的概率密度

气象站由测风仪测得的日平均风速v¯0需要折算到在风机轮毂高度的日平均风速v¯。风速随高度的变化称为风切，通常用如式（1）所示的指数函数来描述风切变换：

其中，z为轮毂高度；z0为气象测风仪的高度；α为地面粗糙度，对开阔地一般取1／7。

已有的研究工作普遍表明一年中每小时平均风速服从Weibull分布[2]。但对于一天24 h的每个小时而言，湍流一般是不能忽略的[2]。湍流指相对短期（如10 min）的风速变化。为更准确地分析不同季节不同天气情况下每天各个时间段的风电机组出力，在每天平均风速的基础上考虑湍流对风机出力的影响是必要的，这较用全年的Weibull分布来统计风电机组出力更为合理。湍流的强度可用式（2）定义：

其中，σv为10 min或1 h以上平均风速的标准差。考虑湍流的风速可粗略表示为服从均值为、标准差为σv的正态分布[2]，其较用全年的服从 Weibull分布的风速能更准确地模拟某季节一天内的风速变化：

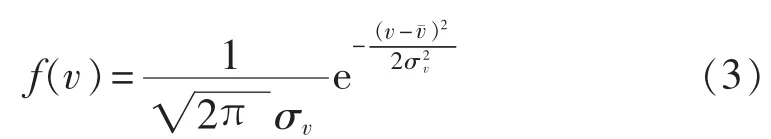
风电机组的输出功率和风速的关系常用式（4）分段线性函数表示：

其中，vin、vN、vout和 PN分别为切入风速、额定风速、切出风速和额定功率（即额定风速下的输出功率）。在已知一个小时内平均风速的概率密度和风机输出功率函数的情况下，即式（3）和（4）已知的情况下，可用式（5）和（6）求得该小时内风电机组的出力概率密度的平均值μPWT与标准差σPWT。

这里简单介绍原点矩与中心矩的概念。设X是随机变量，若 E（Xj）（j=1，2，…）存在，则称它为 X 的j阶原点矩；若[X-E（X）]j（j=1，2，…）的数学期望存在，则称 E[（X-E（X））j] 为 X 的 j阶中心矩，一阶原点矩为变量X的均值，二阶中心矩为变量X的标准差的平方。用MATLAB可求得风电机组出力的j阶中心矩 E[（P（v）-μPWT）j] ；三阶和四阶中心矩将在后面点估计算法中用到。

1.2 光伏发电出力概率密度

气象日值数据中的日照时数是一天内不同辐射强度下的累加值，在已知某日日照时数S的前提下，全天日照辐射总量H如式（7）所示，式（7）体现了日照时数对每天太阳辐射量的影响。

其中，HL为进入地球大气层内的太阳辐射强度；a和b为经验系数；SL为每天日长，单位为h；Ws为时角；H0为地球大气外层的辐射强度；τ 为空气透明系数，τ ∈[0.4，0.8] 。本文采用式（12）描述空气透明系数的概率密度函数[15]。

其中，Φ为纬度；δ为太阳赤纬角，一年中每天的太阳赤纬角是一定的，可以通过查万年历的方法得出；GSC=1.367 kW／m2为太阳常数；E0为地球轨道偏心率校正因子，其可由式（13）计算得到；τmax为空气透明系数最大值；c和λ为与最大空气透明系数及空气透明系数均值相关的量，可由式（14）和（15）求得。

其中，Γ为日角，Γ=2π（l-1）／N，l为一年中的日序数，N为一年的天数，润年时 N=366，平年时N=365；τmean为空气透明系数平均值。

在已知每天的总辐射量H的前提下，从日出到日落各个时段的辐射量占一天内总辐射量的比率可以用式（17）所描述的正态分布来模拟[16]：

其中，t∈[1，24] ；d0和d1均为常系数。正午时日照辐射最强。每小时日照辐射量 H（t）=R（t）H，可按式（19）折算成峰瓦时数。峰瓦时定义为当大气质量为1.5 AM（Air Mass），温度为 25℃，日照强度为1000W／m2的时间。

其中，D（t）为峰瓦时数（单位为 h）；0.0116 为折算系数（单位为 h·cm2／cal）。

光伏电池组每小时的发电量可由式（20）计算：

其中，Ppeak和η分别为光伏电池组的峰瓦功率（W）和效率；WPV（t）的单位为 kW·h。光伏电板在 t时刻的输出功率为 PPV（t）=PpeakηD（t）。用 MATLAB 可以求得 PPV（t）的各阶中心矩。

1.3 电动汽车充／放电功率的概率密度

本文以 PHEV 60（EPRI）[17]为例进行电动汽车充 ／放电概率密度的研究，该电池的容量为18 kW·h，本文电动汽车在充电站中进行集中充／放电，假设充／放电功率恒定为3.6 kW，即充满完全放电的电池需要5 h。设系统中一共有n台电动汽车，考虑到电动汽车的出勤率，每天αn台参与向系统放电的行为。本文采用文献[18] 描述的智能充／放电模式建立每小时接入电网进行充／放电的电动汽车数目模型，即每个时间段内期望接入电网进行充／放电的电动汽车台数如式（21）所示的正态分布。

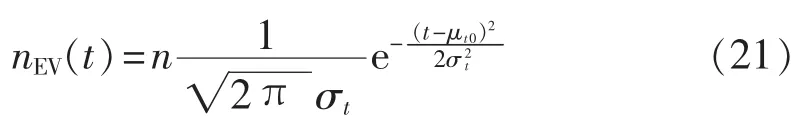
其中，μt0为电动汽车接入电力系统的期望时间；σt为标准差，指充／放电的时间范围。充电的期望时间为 μt0=1，指时段 1，即 00∶00—01∶00，放电时间为 μt0=13，指时段 13，即 12∶00—13∶00，令充／放电的时间分布范围均为σt=2。每个实际时间段内接入电网的电动汽车台数可以用泊松分布模拟，如式（22）所示：

其中，λEV为由式（21）求得的该时间段内接入电动汽车的期望值，nEV为可能接入电网的电动汽车台数。在得到每个小时接入电力系统的电动汽车台数的概率密度函数后，就可以求得该小时电动汽车充／放电功率的均值、标准差和高阶中心矩。

2 考虑天气状况的三点估计法概率潮流模型

2.1 采用三点估计法计算概率潮流

概率潮流方程可用式（23）描述：

其中，g（）表示节点注入功率净向量；Z为待求向量（输出向量），即节点电压的模值和相角；X为已知向量（输入向量），包括一些随机变量和一些确定量，X=（X1，X2，…，Xm，Xm+1，Xm+2，…，XM），X1、X2、...、Xm为随机变量，Xm+1、Xm+2、...、XM为确定量。

点估计法就是在每个随机变量上取若干点进行确定性潮流计算来估计输出量的概率密度。在本文中，随机变量包括负荷的有功和无功、光伏和风电机组的注入功率以及电动汽车充／放电功率。其余变量为常数，如普通PV节点的注入有功功率与节点电压幅值。

三点估计法在每个变量的均值及其两侧取值。每个随机变量集合Xk在均值及其两侧的取值方法如式（24）所示：

其中，E[（Xk-μxk）3] 和E[（Xk-μxk）4] 分别为随机变量集合Xk的三阶中心矩与四阶中心矩。可以采用1.1节介绍的方法求取各阶中心矩。

对于m个随机注入功率，每个变量xk用式（24）确定的3个点分别代替，其他随机注入功率量在均值处取值，即（μx1，μx2，…，μxk-1，xk，r，μxk+1，…，μxm-1，μxm）（r=1，2，3），进行 3 次确定性潮流计算，可以得到待求解的某变量 Zk的 3 个估计值 Z（k，1）、Z（k，2）和Z（k，3）。给定每个随机变量在m个随机变量中的权重为1／m，即这些随机变量的重要性是相同的（如果随机变量的重要性不同，可以给定每个随机变量不同的权重）。对于某一随机变量集合Xk，所取点xk，r的权重为ωk，r，ωk，r的计算方法如式（26）所示：

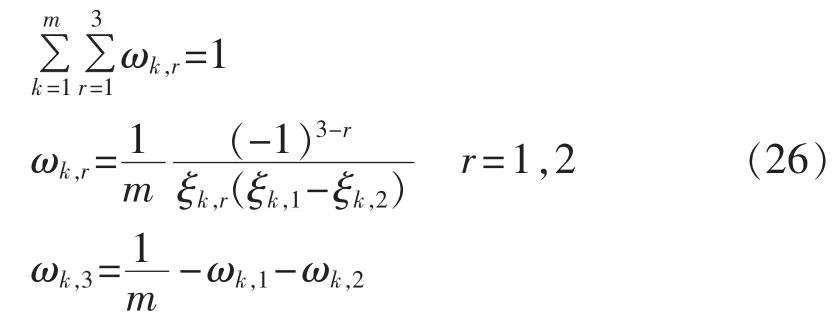
求得每个估计点权重ωk，r后即可利用式（27）求取Zk的j阶原点矩：

其中，Z（k，r）为第k个待求变量的第r个估计值；h（）表示在求解式（23）所表示的概率潮流收敛后，待求向量（输出向量）和已知向量（输入向量）之间的函数关系，即Z=h（X）。Zk的标准差为σZk=。可用潮流输出量（即节点电压、支路潮流等）的统计矩来估计其概率密度函数fZk[19-20]。

对于有m个注入功率随机变量的电力系统，三点估计法需进行2m+1次确定性潮流计算[21]。

2.2 考虑不同季节不同天气状况时每天各小时概率潮流

设某季节有C种可能的天气状况，这样该季节每天第t个小时的节点电压、支路潮流等潮流输出量Zk的概率密度函数可表示为：

3 算例与结果

图1 140节点配电系统Fig.1 140-bus distribution system

以图1所示某140节点配电系统为例来说明所发展的概率潮流模型与求解方法。该配电系统的总负荷为 26.33+j18.61 MV·A；节点 107、123和 136为3个电源点，注入功率分别为6+j3.5 MV·A、4+j2.5 MV·A和7+j4.5 MV·A。馈线的电阻和电抗参数为：r=0.27ω／km，x=0.327ω／km。各线路长度如表 1所示。

表1 线路长度Tab.1 Line lengths

续表

以河北省张北市（北纬41.09°）1995年至2004年这10年间的气象数据为例来仿真多种可能的天气状况。以2011年为例，选取了能表征春夏秋冬4个季节特性的4天：1月10日，4月11日，8月1日，11月21日。所选的这4天的气象信息如表2所示，一年中某天的日序数、太阳赤纬角、日出日落时间是确定的，可以查阅历史数据或由第1节的相关公式计算得到。以1月10日为例，天气状况用1995年至2004年每年1月中每天的平均风速与日照时数来模拟1月10日的不同天气状况。

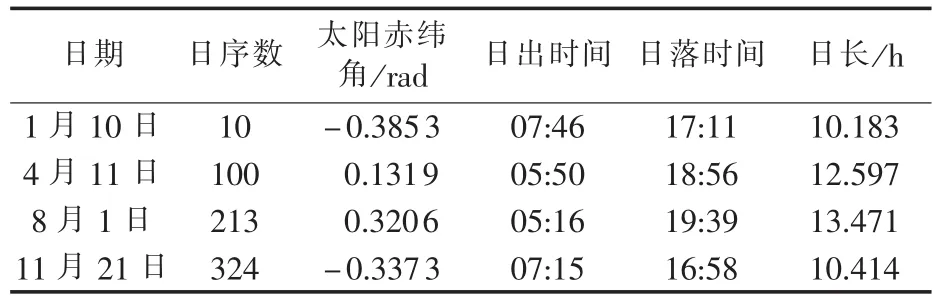
表2 2011年张北气象数据Tab.2 Meteorological data of Zhangbei in 2011

3.1 风力发电机参数

风力发电机组安装在节点122，装机容量15MW，切入风速vin、额定风速vN和切出风速vout分别为3m／s、12 m ／s和 25 m ／s。

3.2 光伏发电参数

光伏发电安装在节点99，峰瓦值为15 MW；根据第1节的计算公式和表2的气象参数可计算出光伏发电系统每小时的发电功率的统计数字特征。

3.3 电动汽车充／放电功率参数

给定：该系统所覆盖区域中共有3500台PHEV 60；电动汽车充电地点为节点138（住宅区），放电地点为节点110（办公区）；每天放电的电动汽车数量为其总量的75%；每辆电动汽车的充／放电功率为3.6 kW；电动汽车电池充／放电时的能量转换效率为0.75；充／放电功率因数为0.99。

3.4 负荷的概率密度参数

这里用正态分布来描述负荷[22]。为更好地模拟4个季节中每天24 h的负荷概率密度，取各负荷节点每小时负荷均值与该节点最大负荷比值 μPnL（t）／μPnLmax都按图2负荷曲线变化。本文中时段1表示00∶00—01∶00，其他时段依此类推。表3给定的系统初始负荷设为0.8μPnLmax，根据图2负荷曲线与原始负荷数据可以计算所有负荷节点每小时的负荷均值。4月11日和11月21日负荷均值与最大负荷值的比值与图2的变化模式一致，而1月10日和8月1日每小时的负荷与最大负荷的比值在图2基础上乘以1.1的系数。每小时的负荷功率服从 N（μPL（t），σ2PL（t））所表示的正态分布，σPL（t）=0.1 μPL（t）。对于无功功率也进行类似处理。

表3 初始负荷Tab.3 Original loads

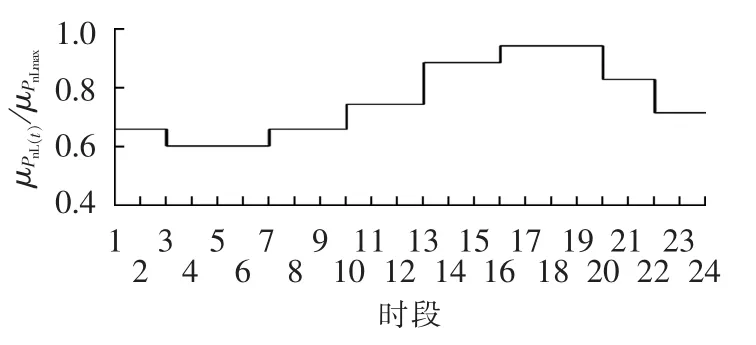
图2 各节点日负荷曲线Fig.2 Daily load curve of each bus

3.5 140节点配电系统仿真结果

以1月10日为例，分别对140节点配电系统有、无电动汽车2种情况进行概率潮流计算；表4列出了有、无电动汽车充／放电情况下各个时间段所有节点平均电压平均值的标幺值。考虑电动汽车充／放电后，在 22∶00至次日 03∶00总体电压水平较低，而03∶00—21∶00之间电压水平相对较高。

表4 1月10日各时间段所有节点平均电压的平均值Tab.4 Average of all bus voltage averages for different daily periods on Jan.10

选取节点62、88和129来分析一天24 h的节点电压幅值的平均值。图3为1月10日3个节点每小时的电压平均值标幺值，节点62和88在00∶00—01∶00电压较低，节点88的平均电压为0.9156 p.u.，而节点 129的电压水平较高。在 12∶00—13∶00之间，节点62和88的平均电压约为0.95 p.u.，而节点129的平均电压约为0.99 p.u.。

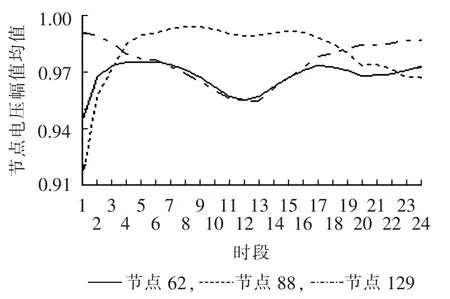
图3 1月10日24 h的3个节点电压均值Fig.3 Average of three bus voltages for 24 hours on Jan.10

图4 1月10日时段12线路127-15的有功功率概率密度函数Fig.4 Active power probabilistic density function of line 127-15 in period 12 on Jan.10

图5 1月10日时段12节点61电压幅值概率密度函数Fig.5 Voltage amplitude probabilistic density function of bus 61 in period 12 on Jan.10

图4和图5分别为用三点估计法和蒙特卡洛仿真方法得到的1月10日11∶00—12∶00线路127-15的有功功率概率密度和节点61的电压幅值概率密度，图5中节点61电压为标幺值。为比较三点估计法概率潮流的准确性，表5列出了用三点估计法和蒙特卡洛仿真方法得到的几个节点在1月10日不同时段的电压均值与标准差标幺值，表6为用三点估计法和蒙特卡洛仿真法得到的几条支路的有功功率的均值与标准差。由表5和表6可知，采用三点估计法求得的潮流量的均值和标准差与采用蒙特卡洛仿真法求得的相应量的偏差在5%以内。

4月11日、8月1日和11月21日这3天系统节点电压在各小时的均值标幺值分别如图6—8所示。可见，在春秋2季负荷相对较小，风电和光伏发电出力相对较高，节点62、88和129的电压水平较好；而夏冬2季电压水平相对较低，尤其是夏季8月，该地区的平均风速为全年最小的月份，所选3个节点的整体电压水平偏低。

表5 部分节点在1月10日不同时段的电压均值与标准差Tab.5 Mean and standard deviation of part bus voltages for different daily periods on Jan.10

表6 部分支路在1月10日不同时段的有功功率均值与标准差Tab.6 Mean and standard deviation of part line active powers for different daily periods on Jan.10

图6 4月11日24 h一些节点电压均值Fig.6 Average of a few bus voltages for 24 hours on Apr.11

图7 8月1日24 h一些节点电压均值Fig.7 Average of a few bus voltages for 24 hours on Aug.1

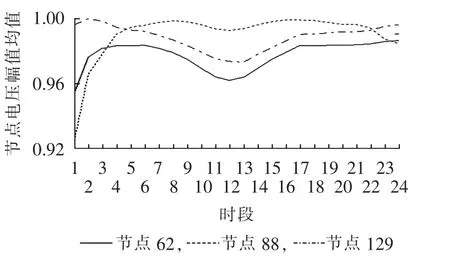
图8 11月21日24 h一些节点电压均值Fig.8 Average of a few bus voltages for 24 hours on Nov.21

4 结语

在可再生能源发电和电动汽车快速发展的背景下，本文发展了含有风光混合发电和电动汽车充电站的电力系统概率潮流计算模型。考虑了风力发电和光伏发电输出功率以及电动汽车充／放电功率的随机特性；导出了风力发电和光伏发电出力的概率密度函数，在此过程中采用气象数据比较真实地模拟了风速与光照强度；导出了电动汽车充／放电的概率密度函数。之后，采用三点估计法求解概率潮流。最后，以140节点配电系统为例对所发展的概率潮流模型和采用的求解方法进行了验证，仿真结果表明所提出的方法得到的结果与采用大量蒙特卡洛仿真所得到的结果相仿，但计算速度比后者快很多。