基于有限元法的切削加工温度场数值分析

胡艳娟，王占礼，李 静，卢 凯

HU Yan-juan，WANG Zhan-li，LI Jing，LU Kai

（长春工业大学 机电工程学院，长春 130012）

0 引言

金属切削加工过程是一个非常复杂的动态性、非线性的工艺过程，常伴随着切削力、切削热和刀具磨损等物理现象。其中，切削热是一个重要的物理参数标志，它直接影响着刀具的磨损、刀具的使用寿命、工件的加工精度以及加工表面的完整性[1,2]。因此，切削温度场的理论研究对分析金属加工原理、预测工件的加工精度以及刀具磨损机理等方面具有重要的意义。

目前，常用的切削温度场研究方法主要有：试验法（如：人工热电偶测温法、红外热像仪法等）、解析法（如：积分变化法、拉普拉斯变化法）和有限元数值法（如：有限差分法、有限元法[3]）。试验法可以得到可靠的数据，但是试验法无法直接得到温度场的分布情况，只能测得某点处的平均温度（如：人工热电偶法）；解析法常常基于各种假设，与实际情况不符；有限元法在解决由材料性质、变形状态和多耦合场引起的非线性问题时，往往表现出其独特的优点，更加接近于实际，同时有限元法可以快速地得到精确的仿真结果[4,5]。综上所述，本文采用有限元数值分析模拟切削加工过程中的温度场分布情况，并与试验结果进行比较。

1 切削热的产生与传出

金属切削加工时，切削热主要来源于三方面：由于切屑最底层金属材料的摩擦和挤压变形所产生的切削热、刀具克服切削层金属的剪切变形做功所产生的切削热以及刀具与已加工表面的摩擦挤压变形所产生的切削热。因此根据上述分析将切削加工时产生的温度场划分为三类，即：剪切区温度场、刀具与切屑接触区温度场以及刀具和工件接触区温度场,如图1所示。

切削加工过程中，切削热大约有80%的热量由刀具克服工件弹塑性变形产生，约18%的切削热有切屑底层材料与刀具间摩擦产生，约2%的热量由刀具与已加工表面间的摩擦产生[6]。大部分切削热由切屑带走（约95%的热量），只有少部分热量残留于工件内。

图1 切削加工过程中产生的热源

2 正交切削模型的建立

金属切削加工时，刀具的主切削刃和副切削刃都参与切削成形，如果车削仿真过程中，同时考虑主、副切削刃参与切削时，会造成金属层在主、副切削刃交汇处产生干涉，从而影响仿真效果。因此本文采用正交切削模型进行仿真。

假设整个仿真过程中，工件材料与刀具材料导热各向同性，且无内热源，金属切削瞬态温度场应该满足二维导热微分方程：

其中：公式（1）与公式（2）中l为热传导率；C为比热；r为材料密度；为单位体积的热产生率；Wh为塑性变形转化为热的比率，本文设定为0.9，为等效应力；为等效应变速率；J为热功当量系数。

2.1 改进的Lagrange网格划分方法

金属切削过程是一个典型的局部变形过程，工件的几何形状与尺寸随仿真时间不断发生变化，并且随着变形的加剧，为了避免仿真时网格发生严重的扭曲变形，采用改进的Lagrange网格划分方法，该方法将Lagrange法和Eu1er法有效地结合在一起，这样划分的网格不会像纯拉格朗日方法出现网格始终跟随材料流动，也不会出现像纯欧拉方法网格始终固定不动[7～9]。同时为了节约仿真时间和计算机存储空间，网格的划分并不是均匀的，而是靠近切削部分的网格划分较细，远离切削部分的网格划分较疏，如图2所示。

图2 改进的Lagrange网格划分

2.2 摩擦模型的建立

由Zorev[10]提出的摩擦模型表明：切屑与刀具前刀面接触区域内存在两种不同的接触状态，即滑动区和黏结区，在黏结区内的各点的切应力基本相同；滑动区内的摩擦应力沿刀具前角而减小，满足库伦摩擦定律。即：

其中：公式（3）中tf为刀屑接触面的摩擦应力；m为摩擦系数；sn为刀屑接触面的正应力；ts为切削材料剪切流动应力。

本文在ABAQUS/Exp1icit仿真器下，刀—屑接触区采用面对面接触（Surface to Surface contact）接触类型采用运动学接触方式（Kinematic contact method），采用有限滑移方式（Finite s1iding），权重因子系数设为0.5。滑动区和黏结区的摩擦系数分别设定为0.4和1。在ABAQUS/Exp1icit仿真器中，可以根据实际的接触应力来判断刀具与切屑之间处于何种接触，从而选择其相对应的摩擦模型，图3是AISI1045钢摩擦模型的接触关系。

图3 AISI1045钢的等厚度摩擦模型

2.3 边界条件设定

工件的尺寸设定为15mm×7.5mm。切削速度方向沿着X轴的负方向，固定工件底边和左边的X、Y、Z方向上的平移和转动自由度。设置工件和刀具的初始温度为室温20℃，分别定义两个接触边界条件，分别为刀具/工件接触条件和工件/工件自接触条件，切屑层网格在刀具前刀面的剪切作用下变形成剪切层，剪切层与切削速度方向之间的夹角为剪切角，如图4所示。

图4 边界条件设定

2.4 本构模型的选择

金属材料切削时通常在高温、高压、大应力及大应变率的环境条件下，为了使仿真结果更加贴近实际，采用Johnson-Cook模型，该模型是一种用于描述金属在大变形、高应变率效应和高温条件下具有良好特性的本构模型，该方程构造简单，应用范围广泛，一般适用于应变率在一个较大范围内（102到106S-1）内应力、应变变化的情况[11]，其表达式如下：

3 AISII045钢切削温度场仿真结果与试验分析

根据上述分析，建立了正交切削有限元模型，得到了AISII045钢切削温度场的分布状况。

3.1 温度场分析

图5是刀具切削AISII045钢仿真得到的温度场云图。从该云图可以看出：切削过程中产生的切削热大部分被切屑带走并且从切削开始到稳定切削时，温度场的分布状况可以分为四个阶段：

第一阶段：初始阶段，如图5（a）所示，切削热主要产生在第一变形区，并且靠近前刀面处切屑上出现了温度密集区，这是由于刀具克服第一变形区内的金属材料大塑性变形而作功产生较高的切削热。

第二阶段：切屑的形成阶段，如图5（b）所示，切削热集中区域转移到第二变形区，且温度最高点并不在刀尖处而是在离刀尖2～3mm。这是由于刀具克服第一变形区内的金属材料大塑性变形而作功产生较高的切削热。刀具前刀面和切屑之间存在着强烈的摩擦，由于摩擦生热使得刀—屑接触区产生较高的切削热。

第三阶段：随着切削过程的进行，切屑进一步形成阶段，如图5（b）所示。切削热的集中区域向第三变形区扩展，这是由于已加工表面与后刀面摩擦而产生切削热。

第四阶段：切屑成形已经进入稳定状态，如图5（c）所示，第二变形区和第三变形区的切削热逐渐沿前刀面向上和沿后刀面向右扩散。这是因为切削速度太快，使得切屑与前刀面或已加工表面和后刀面形成的切削热来不及扩散，从而残留在切屑和已加工表面上。

图5 切削速度为710r/min时的温度场分布

从图6的温度场等值线可知存在很高的温度梯度曲线。由于第一变形区金属材料的大塑性变形而产生了较高的热能，故在刀尖处出现了较高的切削温度；刀具前刀面与切屑间的强烈摩擦热及切屑变形热作用，则在刀尖偏上位置产生了第二高温区，而除此之外的部分的温度相对较低。

图6 切削模型的温度场等值线

从图7切削温度曲线可知：前刀面最高温度为533.2℃，刀尖处温度为342℃。在切削达到2×10-3s时，温度曲线趋于稳定。此时大部分热能由切屑带走，所以温度不在上升，从而趋于平稳。

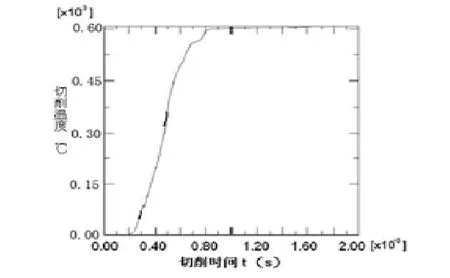
图7 切削温度随时间变化曲线

3.2 试验结果对比分析

为了验证仿真结果，对切削温度进行了试验验证，本试验在CAK 5085dj车床上进行，工件材料为AISI-1045钢，工件直径d=40mm，采用人工热电偶法对切削温度进行测量，测量结果如图8、图9、图10所示。

图8 不同切削速度下切削温度值

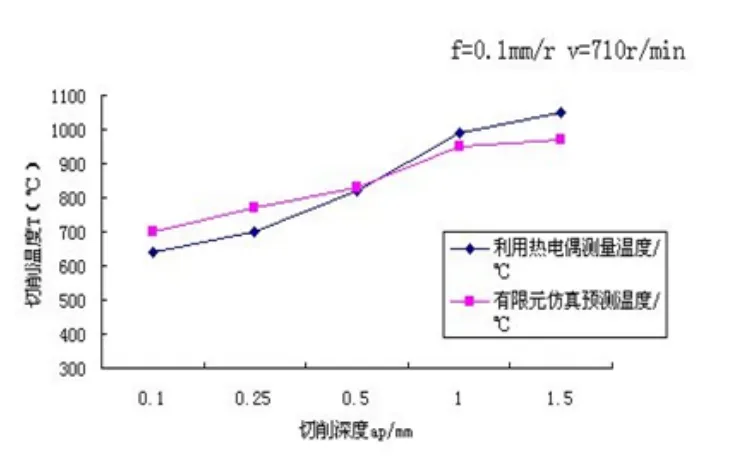
图9 不同切削深度下切削温度值

图10 不同切削深度下切削温度值

通过对比发现，所有的仿真结果跟试验结果都非常吻合，这说明所建立的有限元模型不仅可以得到较为准确的温度场数值，而且在不同参数下其仿真结果同样准确，从上图中不难看出：对切削温度场影响较大的因素为切削速度、切削深度和进给量。随着切削速度、切削深度、进给量的不断增加，切削温度也是不断增加的。

4 结论

1）通过利用有限元法仿真得到的切削温度值和实测值对比表明：在试验数据范围内，该方法具有很高的预测精度。且它相对应于其他方法（如：试验法、解析法）可以得到金属车削过程中无法直接测量或根本测量不到的温度场分布情况。

2）从仿真结果和实测值可以看出：实际切削加工中，对温度场影响加大的因素为切削速度、进给量和切削深度，随着切削三要素的增加，切削温度呈现增大的趋势。

3）本文建立的二维温度场模型与实际情况是相符的，但是如果需要进一步考虑刀具斜角对切削温度场影响情况时，可以选择建立三维模型进行研究，这部分工作也具有重要的物理意义和应用价值。

[1] 胡艳艳,费树岷,韦皆顶.高速加工切削热产生机理及监控技术研究综述[J].中国制造业信息化(学术版),2007,36(10)∶93-97.

[2] N A Abukhshim,P T Mativenga,M A Sheikh. Heat generation and temperature prediction in meta1 cutting∶A review and imp1ications for high speed machining [J].Internationa1 Journa1 of Machine Too1s & Manufacture(S0890-6950),2006,46∶782-800.

[3] R Komanduri,Z B Hou. A review of the experimenta1 techniques for the measurement of heat and temperatures generated insome manufacturing processes and tribo1ogy[J].Tribo1ogy Internationa1(S0301-679X),2001,34∶653-682.

[4] R C Dewes,E Ng,K S Chua,et a1. Temperature measurement when high speed machining mou1d/die stee1[J].Journa1 of Materia1s Processing Techno1ogy (S0924-0136),1999,92-93∶293-301.

[5] O Caste11anos,M Shat1a,T A1tan. Prediction of stresses,temperatures and too1 wear in meta1 cutting using FEM.[M]// ERC/NSM Report No. HPM/ ERC/ NSM-99–R–11.USA∶ The Ohio State University,1999.

[6] 张伯霖.高速切削技术及应用[M].北京∶机械工业出版社,2002.

[7] Kug Weon Kim,Hyo-Cho1 Sin.Finite E1ement Method and Thermo-Viseop1astic Cutting Mode1 in Manufacture System [M].Tokyo,Japan∶CRC Press LLC,2001.

[8] Mahmoud Shat1a,Christian Kerk,Tay1an A1tan. Process mode1ing in machining. Part II∶va1idation and app1ications of the determined f1ow stress data[J].Internationa1 Journa1 of Machine Too1s & Manufacture(S0890-6955),2001,41∶1659-1680.

[9] P L B Ox1ey.Mechanics of Machining∶AnAna1ytica1Approach to Assessing Machinabi1ity[M].New York,USA∶Ha1sted Press,John Wi1ey & Sons Limited,1989.

[10] Zorev N N.Inter-re1ationship between Shear Processes Occurring a1ong Too1 Face and on Shear p1ane in Meta1 Cutting[C]//Internationa1 Research in Production Engineering.New York∶ASME,1963∶42-49.

[11] 李圆圆.高速切削淬硬钢切屑形成过程及温度场有限模拟研究[M].大连∶大连理工大学.2008.

[12] Avira1 Shrot,Martin Baker.Determination of Johnson-Cook Parameters from machining simu1ations[J].Computationa1 Materia1s Science,2012,52(1)∶298-304.