钢轨轨腰圆孔集中应力变形的理论与实验研究

2013-10-17王宏伟王春明于冠东

制造业自动化 2013年24期

王宏伟，王春明，于冠东

WANG Hong-wei,WANG Chun-ming,YU Guan-Dong

（包头钢铁职业技术学院，包头 014010）

0 引言

铁路钢轨承载着火车运行的主要任务，同时也是感测铁路信号的重要载体。为了实现对列车的自动控制，必须实时监测其运行状态。钢轨在列车经过的瞬间，一定会在电、磁、声等各方面产生变化[1]。同时，列车从钢轨上经过，钢轨在承受巨大载荷的同时，也一定会产生一个相当复杂的变形。从原理来看，作为感测对象，钢轨承载变形在以上提到的诸多物理量变化中应该是最直观可靠的，不易造成其他信号的扰乱。但是，经大量理论、实验研究证明，列车经过轮轨的瞬间，其变形量非常微小[2]，因此感测铁轨变形非常困难。经过实验数据比对，我们另辟蹊径，设计了一套方案：由于应力集中会使承载变形加剧，从而达到易于感测、准确感测这一物理量的目的，所以在钢轨本体设计产生应力集中的结构。

1 人为增加集中应力结构的方案选取

一般来说，实际的构件，在有圆孔、缺口等处，由于其横截面的形状发生突变，造成局部地方发生非常大的应力，这就是应力集中现象。应力集中会造成变形量急剧增大，但同时一些应力集中会使钢轨产生裂纹，长期会失效，严重降低强度。所以在分析了多种人为增加应力集中结构的方案后，得出结论：在钢轨轨腰处钻孔是最佳选择。主要原因有两点：

1）在铺设钢轨时要有必需的节节连接，所以钢轨本身在制造过程中就有钻孔的结构设计。这就简化了安装成本，利于检测元件的普及。

2）结合圆孔设计的传感器在结构上容易给予相应的补偿措施，最大限度的弥补由应力集中削弱的钢轨强度。

因此，在钢轨的轨腰处，钻一个直径约30mm的孔(如图1所示)。在火车载荷作用下，孔的周围会产生应力集中。通过人为增加应力集中变形，使感测对象更易于测量。

图1 钢轨上孔的应力集中变形示意图

2 选取由于应力集中产生变形的最佳测试对象

对于一个承载后的钢轨，其轨腰处孔变形量最大的位置就是我们要找的监测点，即最佳测试对象。

2.1 建立力学模型

为了容易展开研究，问题简单化，首先建立力学模型。把钢轨当做平面梁，并且其上受到集中载荷的压力。锁定研究对象为枕木上端的一段钢轨。此处，有两点简化，使之成为平面问题：

1）钢轨横截面由原来的变截面看成等厚平板，厚度为b（力的传递性）；

2）假定钢轨承受作用力（F）在宽度方向上是均布的，则可得载荷（P）如下式：

2.2 集中应力产生的最大应力σmax和测试点的确定

根据以上力学模型的建立，我们将问题简化为有一个圆孔的无限扳承受均匀压力的情况（如图2），圆孔半径为r。在圆孔周围将产生应力集中现象，其各点应力分布状态可用以圆孔中心O为原点的极坐标r、θ表示如下[3]：

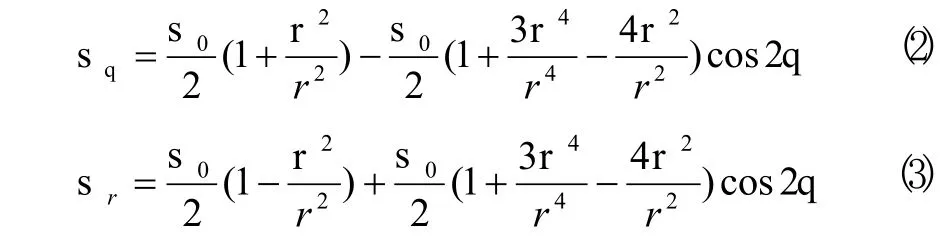
其中 σ0为基准应力。

对式(2)和式(3)求导，得到应力的最大值将出现在点A(r=r q=p/ 2,3p/2)，最大值为：

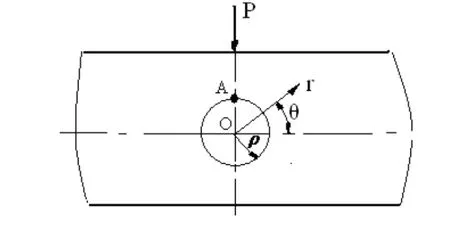
图2 力学模型

可见，载荷作用线刚好经过枕木正上方时，孔在载荷作用线上的直径变化量是最大变形量。由此，孔的圆度将发生如图1的变化，由圆形变为椭圆形，可见其直径差 (Δd)max=f d−fd′是最佳测试对象。以下将从理论计算和实验研究两方面来具体确定这个变形量。

3 理论计算

3.1 基准应力σ0的确定

根据基准应力的选取方法[3]：在没有应力集中的基准应力分布已经不是均匀分布的情况下，要选取假定没有应力集中因素时可能产生的应力为基准应力。

在钢轨枕木上端的一段，其轨腰处的应力是一个接触应力，分布是不均匀的[2]。其受力曲线呈现正态分布，即在轨腰的载荷作用力线上最大，并以其为中心，在轨腰长度方向上，分别向两边对称快速的正态衰减。在应力集中系数一定的情况下，最大应力点也就是在标准应力最大的地方。即在没有应力集中因素时可能产生的最大的应力点位置。因此，我们将载荷作用线上或者说孔中心线上与孔上边缘交点A点（见图1）在未钻孔之前的应力作为应力集中分析的基准应力。则[4]：

式中：P为作用于钢轨上的载荷；

h为A点与载荷P作用点C的距离。

3.2 理论计算推导

在未钻孔前，A点的垂直位移量计算：

A点在载荷作用线上径向位移（即垂直位移量）u取得最大值（水平方向位移量v(θ=0)=0为）[2]：

式中：E为材料的弹性模量，对于钢轨材料，E=210GPa；

H为假设位移为0的点M距载荷作用点C的垂直距离。在此为钢轨全高。

那么，由于集中应力的影响，圆孔在载荷作用线上，其直径的最大变形量计算公式如下[5]：

b为应力变形系数，即相同的载荷作用下，同一点在有应力集中的位移量是无应力集中的位移量的倍数。这个值也说明了采取应力集中使感测目标实际扩大的倍数。也是本论题的研究意义在数值上的具体体现。

对于在实验中，我们应用的50钢轨，其结构尺寸如图3所示，将各数据带入式9，可得：b50=3.848。如果是60钢，同样根据其结构尺寸，计算出b60＝3.785。可见，随着钢轨重型尺寸的增大，其应力集中产生的相对变形量也越小。

图3 50钢轨结构尺寸图

3.3 理论计算值

下面，以50钢轨为例，计算其在各载荷作用下，轨腰处直径为Ø30mm的孔的直径最大变形量(Δd)max（将各尺寸带入式(8)）。结果见表1计算形变量一列。

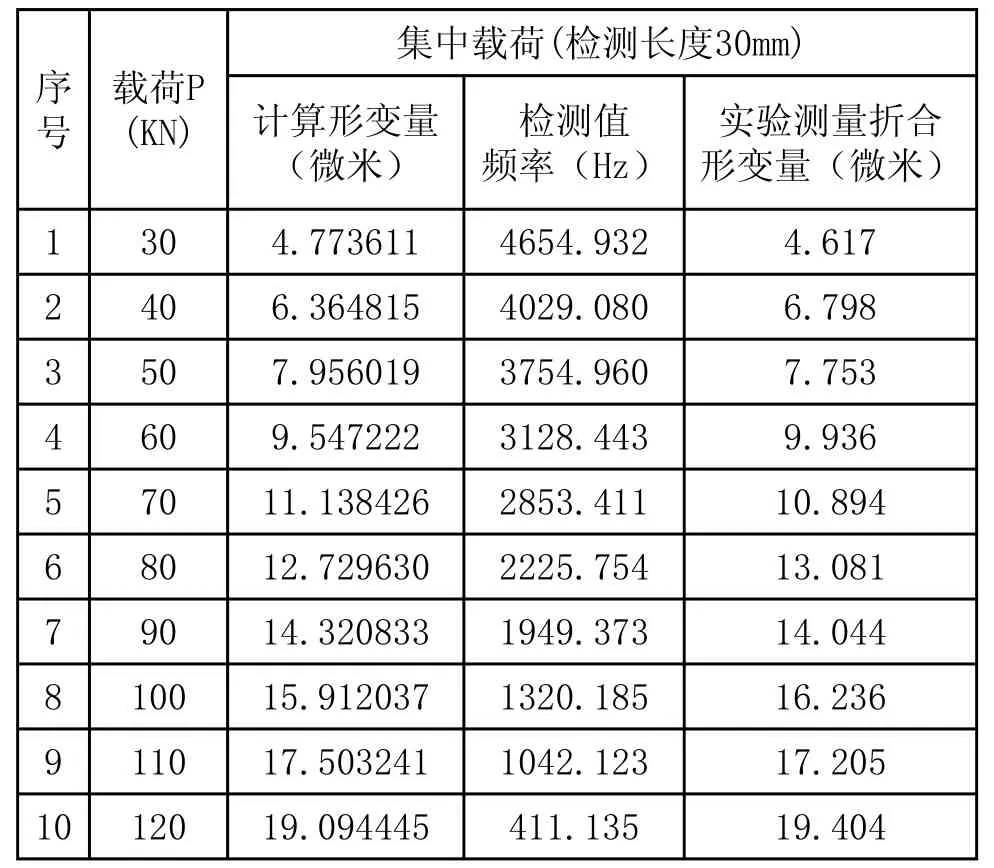
表1 孔变形量计算值和测量值对比表

经力学校核：检测灵敏度约为 287赫兹/1微米。

4 实验测量

由于应力集中问题非常复杂，为简化问题提出太多假设，所以理论计算值的准确度也会大打折扣。所以，在理论计算的基础上做实验测量验证，是非常有必要的。下面对轨腰处直径为Ø30mm孔的最大变形量 (Δd)max进行真实的实验测量。

4.1 自制测量仪器的结构

经理论计算所得，检测目标 (Δd)max值虽然有所放大，但仍是微米级的量，所以我们选择电容式传感器作为结构设计的基础[6]，并自制了精确的测量装置，可以准确地感测检测对象。具体电容式测量装置的结构图如图4所示。

仪器由电容上极板组合体、下极板组合体、屏蔽外壳及端盖组成。由于感测信号极其微弱，极易受到来自外界信号的干扰，所以，设计双层的全封闭屏蔽外壳。将与电容下极板相连的下极板组合体至于其中，并与外壳内层粘接形成一体。将带有电容上极板的上极板组合体插入已经粘接了下极板组合体的外壳内，使电容上下极板间形成一个固定的微距离，同时将屏蔽外壳上平面封闭，最后盖上后端盖，形成全封闭结构（如图5所示）。

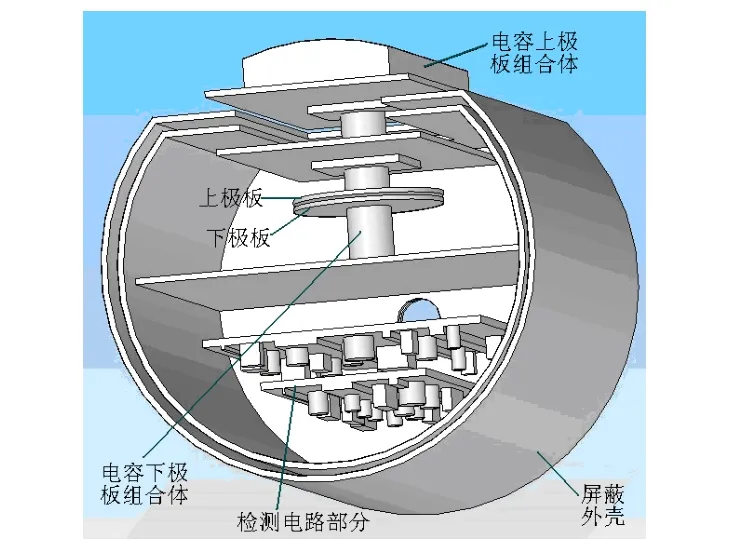
图4 测量装置装配图

图5 测量装置组装过程

4.2 测量过程及工作原理

测量前，首先将上极板组合体对正粘结在图1中相当于A点的位置，然后将已经粘接了下极板组合体的外壳与上极板组合体装配好，并将其与圆孔下部粘接固定好。

测量时，在事先标好的圆孔中心线上逐步施加载荷P(如图1所示)。钢轨圆孔受到载荷P的作用，其圆度发生变形，孔在载荷作用线上圆孔的上下面由于分别与电容上下极板粘接固定，所以会分别带动上下极板运动，使圆孔直径的最大变形量1：1的反应为电容两极板间距离的改变。通过与之相连的检测电路，就可检测到圆孔直径的最大变形量。