基于相关性的自适应阈值去噪方法研究

袁丽英，张 蕊，徐 鹏，刘仲杰，荆 宇

(哈尔滨理工大学自动化学院，哈尔滨150080)

在图像的采集和传输过程中，不可避免地带入噪声，从而影响图像的质量.如何更有效的提取图像中的实际信号，最小化与原始图像的差别，研究人员进行了相关的去噪研究.传统的图像去噪方法多采用平均或线性方法，去噪效果不够理想.随着小波理论的完善，小波分析在实际中得到了广泛的应用，此方面的研究成果也非常之多.Donoho提出了一种小波阈值去噪法［1］，能够有效的去除噪声，因为实现简单，得到广泛应用.随着对图像质量要求的越来越高，传统的阈值方法已经不能满足要求，为了提高阈值方法的去噪效果，学者们进行了一系列的研究和改进.

图像经小波变换后，各尺度间相应位置上的变换域系数具有较强的相关性，利用这一特点，出现了几种常用的相关性去噪算法，如Mallat提出的基于小波变换域内系数相关性的滤波算法［2］，Xu提出的小波相关去噪算法SSNF［3］.因尺度间小波系数偏移的原因，通常的相关算法中存在判断准确率过低的缺点，虽然SSNF算法有效的弥补了这一不足，但仍存在信号边缘不突出的缺点［4］.针对SSNF算法的不足，文献［5］提出一种基于小波系数相关性的去噪方法，较好的保留了图像的边缘，但是这种算法计算量大，且去噪效果并不明显.本文对此算法进行改进，提出了一种基于相关性的自适应阈值去噪算法.

1 对数阈值函数

虽然软、硬阈值法在实际应用中取得了较好的效果，但其本身仍存在着一些不足.硬阈值虽能够保留更多的图像边缘细节，但由于其阈值函数不连续，会引起去噪图像中出现振铃、伪吉布斯效应;软阈值处理可以弥补硬阈值算法的不足，但由于存在固有的偏差，会造成图像模糊.针对这个问题，文献［6］提出了折衷阈值函数，阈值函数如式(1)所示.

折衷阈值算法在一定程度上综合了软、应阈值算法的优势，但去噪效果提高并不明显.针对硬阈值函数、软阈值函数以及折衷阈值函伪进行研究，发现比较合理的阈值函数需满足:

1)为减少振铃、伪吉布斯效应，新阈值阈值函数应为连续函数，使得图像处理时相对平滑.

2)为了较好的保留图像边缘细节，应保持表示信号的小波系数保持不变.这里以折衷阈值函数为基础，增加阈值函数的自适应性，满足下面要求:

1)当|x|的值接近阈值时，容易产生振铃和伪吉布斯效应，考虑软阈值函数的优点，故α的值应趋近于1.

2)当|x|的值增大时，应尽量保持图像边缘细节，考虑硬阈值函数的优点，故α的值应迅速趋近于0.

根据上述要求，以及对文献［6］中的改进阈值函数进行比较，提出对数阈值函数如下:

其中:β取值为［0，+∞).当|x|＞δ时，阈值函数高阶可导，便于进行各种数学处理.

对新阈值函数进一步讨论，参考如下函数，

可以得出，阈值函数以直线f(x)=x为渐近线，实现了从软阈值到硬阈值的平滑过渡，克服了软阈值函数与原始值存在偏差以及硬阈值函数不连续的缺点.

根据式(2)可得

可知当β=0时，阈值函数为软阈值函数，当β→+∞，阈值函数为硬阈值函数.可见，通过调整β的取值可以改变从软阈值到硬阈值过渡速度，β越小过渡速度越慢.通过调整β的取值，可得到实用有效的阈值函数.

2 阈值选取

实验证明，含噪声图的第1级小波分解子带系数方差几乎等于噪声方差.而随着分解级数的增加，噪声在系数方差中所占的比重越来越小［7－8］.

考虑不同尺度间小波系数噪声和信号的不同特性，单一的使用全局阈值并不合理，应针对不同尺度中的系数计算阈值.根据文献［9］可知，第1级分解比例系数近似等于1，第2级分解比例系数比第一级略小，第3级及以上比例系数近似于1/2～1/3，由此规律得到阈值选取公式如下:

其中:j为小波分解的层数.

比例系数函数如下

取x=1～5，计算y值，得到数据如表1所示.

表1 比例系数表

由表1可知，次阈值选取公式的比例系数满足文献［9］提出的比例系数关系.

3 基于相关性阈值去噪

噪声图像经小波分解后，实际信号具有强相关性，而由于噪声信号为随机分布，其表现为弱相关或者不相关［10－11］.

根据实际信号与噪声信号相关性的差异，考虑采用相关性的方法进行噪声系数判断.文献［5］提出的算法通过计算高频与低频的相关系数进行去噪处理，但因图像中包含相关性噪声很少，且呈弱相关性，此算法计算全部高频系数相关性，计算量大且去噪效果并不理想，本文针对这一不足对其改进.

根据公式

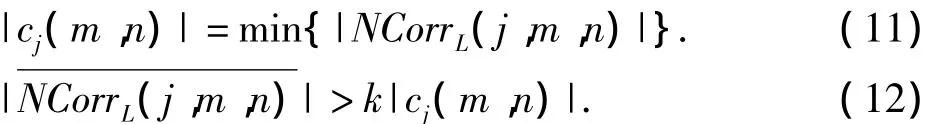
可以判断若相关系数大于最低系数的倍，则认为其为图像信号，否则为噪声.

这里，设

根据式(13)定义相关量

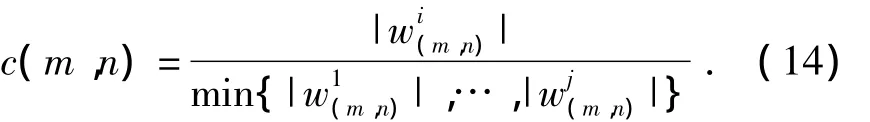
当c∈［1，γ)时，说明小波系数相关性较强，为图像信号;否则，小波系数为弱相关性或者不相关，为噪声信号.可见γ的取值影响尺度间相关性判断效果如果，若γ取值过于接近1，则相关性估计过于严格，若取值过大则会使过多噪声入选，影响去噪效果.

计算相关量时需将各尺度相应子带的小波系数扩充至相同尺寸.因邻近尺度间相关的小波系数以2×2的尺寸相对应，所以应采用2×2的方式进行扩充.但随着分解层数的增多，系数扩充的难度会随之增大，故此方法适用于分解层数较低的情况下.

基于相关性阈值去噪算法具体流程图如图1所示.

图1 基于相关性阈值算法流程图

4 实验结果与分析

本文采用Matlab2010a软件，将几种阈值去噪方法与本文去噪方法进行对比试验，采用峰值信噪比(RPSN)作为去噪效果测度指标.以灰度图像为测试图像，加以标准方差σ为0.008～0.400的高斯噪声，用bior3.7滤波器进行试验，分解层数为3.

经过大量实验得到，β=0.4时本文去噪方法能够取得相对较好效果.尺度间相关性估计采用较严格策略，取值为γ=2.

实验具体步骤如下:

1)将灰度图像加入σ=0.01的高斯噪声.

2)将噪声图像进行3层双正交小波分解，并根据式(9)计算每层小波系数阈值.

3)对小波系数进行阈值判断，对处在阈值边缘的系数按照式(14)计算相关量，并根据尺度间相关性估计策略进行判断，强相关性为图像信号，弱相关或不相关为噪声信号.

4)根据式(2)进行阈值去噪，并对所得的新小波系数进行重构，得到去噪后的灰度图像.

此次试验的去噪效果对比如图2所示.

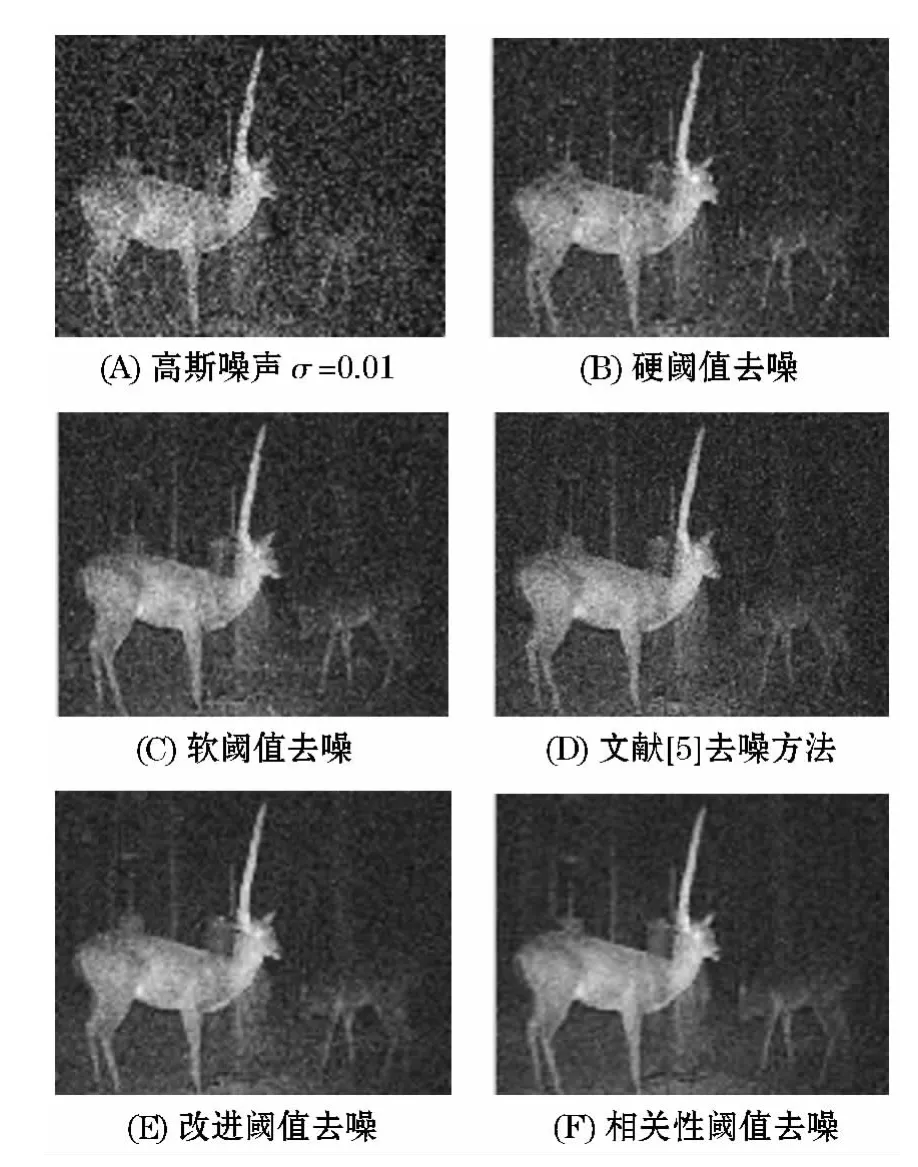
图2 图像去噪效果对比

将基于相关性阈值去噪算法与软阈值、硬阈值、改进阈值以及文献［5］提出的算法进行去噪效果比较，明显可以看出本文算法取得了更好的去噪效果.通过表2可知，对不同程度的噪声影响，本文算法均得到较高的峰值信噪比.

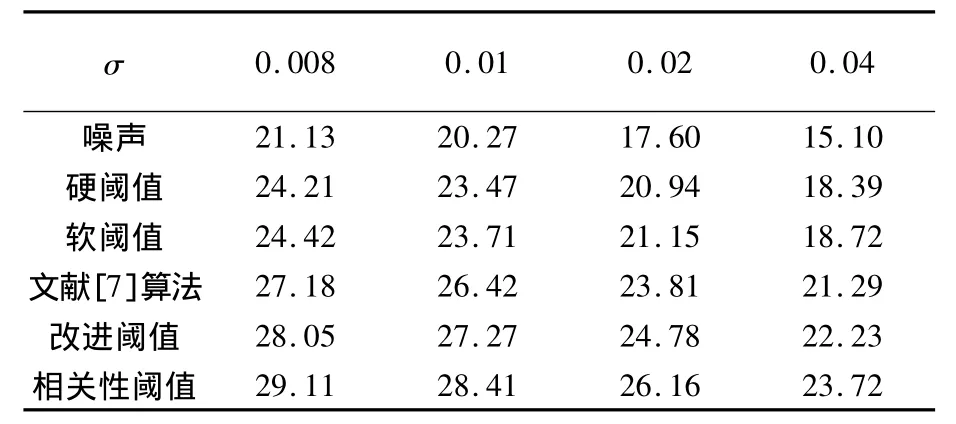
表2 不同算法下高斯噪声图像R PSN比较

5 结语

本文针对软硬阈值去噪的不足提出一种新阈值去噪算法，并结合相关性处理的方法，得到新的图像去噪方法.经过与多种算法去噪视觉效果比较以及峰值信噪比评价，证明基于相关性阈值算法去噪效果更好，去噪后图像与其他去噪图像相比更清晰.但此算法仍存在边缘细节受损及清晰度变差的缺点，因此需要对小波变换去噪方法做进一步的研究和改进.

［1］DONOHO D L.De－ noising by soft－ thresholding［J］.IEEE Trans Inform Theory，1995，41(3):613 －627.

［2］PAN Q，ZHANG L，DAI G，etal.Twode － noising methods by wavelet transform［J］.EEE Trans.on SP，1999，47(12):3401－3406.

［3］SUNTNEUVOY.Detail－ preserving median based filters in image processing［J］.Pattern Recognition Letters，1994，15(4):341–345.

［4］毛 伟，林春生，吴正国.一种基于SSNF的新型阈值滤波去噪算法［J］.海军工程大学学报，2007，19(6):75 －78.

［5］蔡良师，郑南山.基于小波系数相关性的图像去噪［J］.测绘科学，2012，37(1):94 －95.

［6］LI Y C，SUN J P，FU X J.Infrared image denoising based on wavelet transform［J］.Laser and Infrared，2006，36(10):988 －991.

［7］XU Y S，WEAVER JB，HEALY D M，etal.Wavelet transform domain filters:a spatially selective noise filter ration technique［C］//IEEE Trans.On Image Process，1994(s):747－758.

［8］张 鑫，井西利.一种基于正态反高斯模型的贝叶斯图像去噪方法［J］.光学学报，2010，30(1):70 －74.

［9］刘洲峰，程 寅.一种基于改进阈值函数的小波图像去噪算法［J］.中原工学院学报，2010，21(2):43 －45.

［10］YU M，YI W J，JIANG G Y.Image denoise based on interscale correlations of Contourlet transform［J］.Optoelectronic Engineering，2006，33(6):73 －77，83.

［11］袁丽英，孙莉莉.基于小波线性最小均方误差的红外图像去噪［J］.哈尔滨商业大学学报:自然科学版，2012，28(4):439－443.