基于圆谐-傅里叶矩与支持向量机的癌细胞识别

刘应钦，李红梅，白尚旺

（太原科技大学计算机学院软件工程教研室，太原 030024）

在癌症检查中，通常需要对病人的痰液或尿液中细胞进行涂片，使用显微技术进行识别与分析。这项工作较为繁复，并且误判概率较大，因而需要计算机辅助医疗技术，代替人工来对细胞是否病变进行判定，从而将医生从繁复的劳动中解脱出来。

目前使用计算机辅助诊断技术对细胞识别时准确率总是不高。究其原因，是由于在识别细胞图像时，通常首先要将细胞与其他细胞进行分割，而后对该细胞的一组特征，如细胞总体积，细胞形状，细胞核形状，细胞核浆比，细胞内纹理结构等，最后运用这些特征对其是否发生癌变进行判定［1-3］。但是细胞的种类繁多，不同的细胞体积与形状都不同。即使是相同种类的细胞，如果处在不同的时期，其外观通常也不尽相同。这种情况下，就使得对于不同种类，不同生长阶段的细胞，需要使用不同的，带有针对性的细胞特征来分辨与判断其是否病变。这就给识别工作带来了很大的困难。

由于这些问题，Snake［4］算法便是通过使用能量函数作为度量值，将图像的分割线与图像相联系，使用最小化能量泛函来约束分割线，以得到最佳的分割效果。本文采用圆谐傅里叶矩作为图像的特征，然后利用支持向量机将提取的图像矩进行优化，便可以得到一套准确、快捷的细胞识别算法。

1 圆谐-傅里叶矩

1.1 圆谐-傅里叶矩介绍

图像矩是一种高度浓缩的图像特征，它具有平移、旋转、灰度、缩放不变性，这使得图像矩对由于光照、色彩、角度不同而造成的图像畸变不敏感，因而适合被用来描述图像，作为图像的特征值［5-7］。

圆谐-傅里叶矩的结构是由三角函数作为其径向函数Tn（r），与圆谐波函数exp（jmθ）相乘，构成函数系 Pnm（r，θ）:Pnm（r，θ）=Tn（r）exp（jmθ）

其中，径向函数Tn（r）定义为:

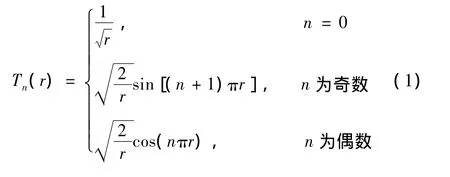
很显然，函数系Pnm（r，θ）在区间0≤r≤1之内是正交的:

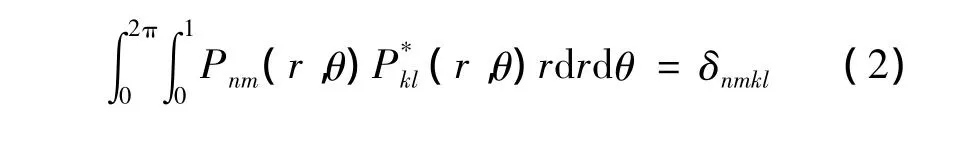
定义圆谐-傅里叶矩的计算公式为:

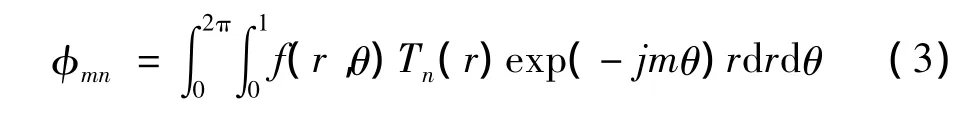
由于该矩为正交矩，则可由无数个圆谐-傅里叶矩重构图形，其公式为:

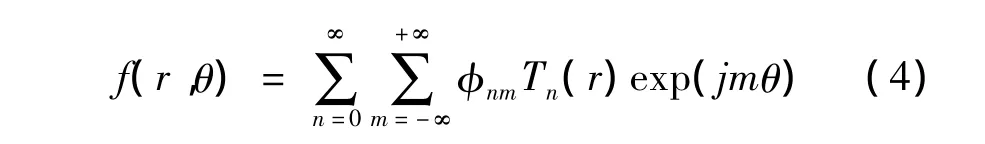
1.2 圆谐-傅里叶矩的性能与分析

对图像矩中的径向函数而言，零点的数目与位置通常与其描述的图像空间频率成分有关。也就是说，一个n阶的径向函数的零点位置与数目，代表了该径向函数对图像的采样位置与频率［9］。如果零点数目过少，则采样次数较少；如果零点位置分布很不均衡，则会造成图像部分采样较多，另一些部分采样较少，都不能很好的描述图像。

对于图像矩而言，零点的数量与分布决定了对图像描述能力的强弱［6］。对圆谐-傅里叶矩的径向函数Tn（r）求零点，得到结果如图1所示。

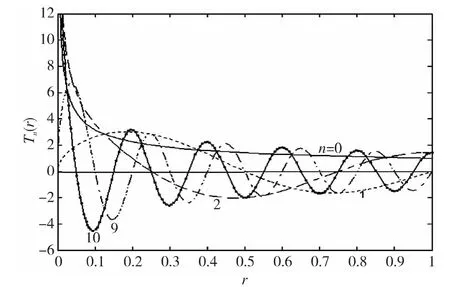
图1 Tn（r）零点分布图Fig.1 Tn（r）zero maps

由图1可看出，n阶圆谐-傅里叶矩的零点数目多于n个，且分布均匀，这就使得圆谐-傅里叶矩对图像的中心与边缘的描述是平均的，不会由于零点位置的不均等造成部分图像特征提取的失真。而第一个零点非常接近坐标原点，这就使利用该矩进行小图像描述的效果较好。

2 支持向量机

2.1 支持向量机简介

支持向量机是一种新的机器学习方法，它是由Vapnik［8，10］等人提出的利用统计学习理论中 VC 维理论及结构风险最小化理论，通过恰当的选择函数子集与该子集的判别函数，利用有限样本，兼顾模型复杂度与模型学习能力，使模型的结构风险达到最小，以此使模型得到优良的泛化性能。同时，它具有全局优化，适应性较强，训练时间较短，泛化能力较好的特点。由于其引入了核函数，支持向量机很好的解决了非线性分类的“维度灾难”的问题，使得其运算效率进一步提高。

2.2 最优超平面

支持向量机是由对样本线性可分的情况下，寻找广义最优分类面的问题发展而来的。假设一个两类训练样本集中有1个n维样本，则需要找到一个分类面，将这两类训练样本尽可能的分开。设该分类面为一超平面，则该超平面可以表示为:（ωx）+b=0，其中，ω为超平面的法线方向，为单位法向量，‖ω‖为ω的欧氏模函数。于是，将所有样本正确分类的公式为:

在实际中，能够将样本D成功划分的超平面很多。而我们需要寻找这样一个超平面:不仅可以将样本集正确分开，而且使距离超平面最近的两类样本点的间隔最大。能够正确划分超平面，是使支持向量机的经验风险最小；使分类间隔最大，则是使VC维最小，减小了置信范围，使支持向量机具有最优的泛化能力。这个超平面在众多分类面中是唯一的，通常被称为最优超平面，如图2所示。

其中，H为能够将两类样本正确划分的超平面，H1，H2为经过距离最优超平面最近的样本点，且与最优超平面平行的平面。而在H1与H2上的点被称为支持向量。H1与H2之间的间隔被称为分类间隔。

由图 2可看出，H1与 H2与 H的间隔为1/‖ω‖，这使得分类间隔为2/‖ω‖.而寻找最优超平面的问题，可以由此转化为寻找分类间隔最大，即是使‖ω‖2最小的问题。这个问题的转化，体现了对支持向量机推广能力的提升。寻找最大间隔，就是使之具有最优的泛化能力。

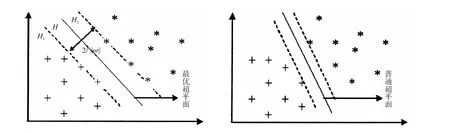
图2 最优分类面示意图Fig.2 The surface diagram of optimal classification

当遇到线性不可分的情况下，如果将其强行分开，则很容易产生过度拟合现象。针对这一问题，Cortes和Vapnik引入了软间隔最优超平面的概念。

在线性可分状态基础上，在计算中引入松弛变量 εi≥0（i=1，2，3…l），则可以使模型允许一定的噪声或错误样本出现。之后对目标函数加入惩罚因子C，于是原始问题变为:

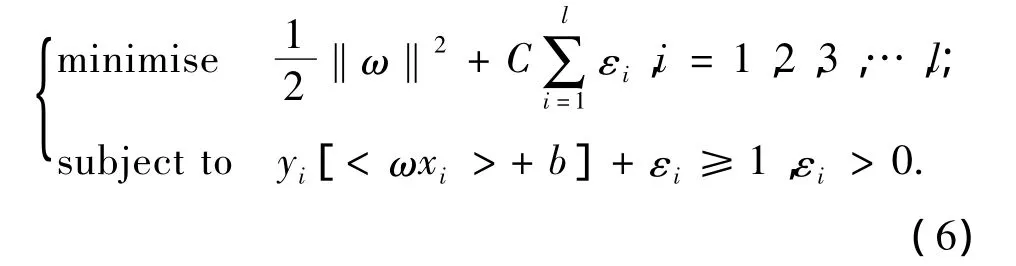
惩罚因子C＞0是对目标函数中错分样本程度的控制。若C增大，则在最有分类面周围区域中，可错分的面积越小。若C为无穷大，则该算法退化为在线性可分情况下的分类算法。

则最优分类面也由下式得出:

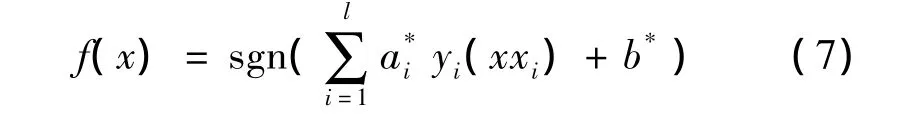
其中，0≤ai≤C说明了惩罚因子C控制了ai的大小，即约束了可以接受的离群点的范围。而离群点的拉格朗日乘子通常较大，使得约束确保了可行区域的界，从而使问题总是有非空的可行区域。

此时，最优解a*可以有三种情况:

若是a*=C，则表示a*所对应的样本未在隔离带的边界上，但被错误分类，属于支持向量，参与构建最优分类面；

若是0＜a*＜C，则表示a*所对应的样本在隔离带的边界上，属于支持向量，参与构建最优分类面；

若是a*=0，则表示a*所对应的样本不在边界上，属于非支持向量，不参与构建最优分类面。

针对非线性的分类，支持向量机算法引入了核函数的概念。即有非线性映射Φ∶Rd→H，使空间Rd中的低维非线性样本映射入高维空间H中成为线性可分样本。可以看出，支持向量机寻找最优分类面时，仅仅需要计算样本的点积Φ（xi）·Φ（xj）即可，无需单独计算单个映射Φ（xi）.于是，如果能够找到一个合适的函数K，使得K（xi，xj）=Φ（xi）·Φ（xj）.因此只需要在高维空间中进行内积运算，而不用将函数空间进行提升，甚至不需要了解变换Φ（xi）的具体形式。这个函数K便被称为核函数。

根据泛函分析的相关理论，核函数只需满足Mercer条件，就可以计算低维样本对应于某高维空间的高维内积。于是，支持向量机的对偶问题变为:

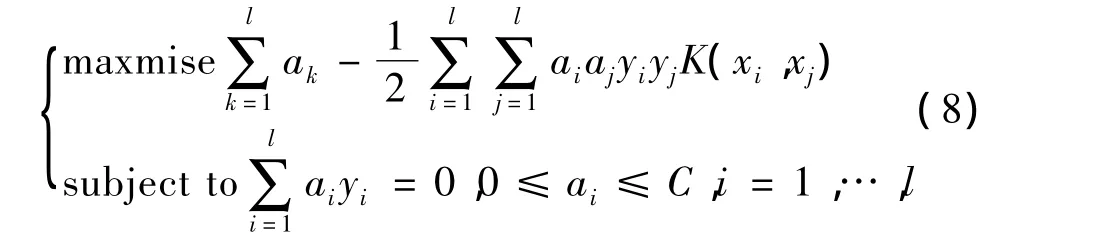
这样，非线性可分样本计算内积的工作将在低维空间中完成，映射入高维线性空间所增加的计算量很少，支持向量机整体的计算复杂度并没有多少增加。其对应的最优分类面决策函数也变形为:

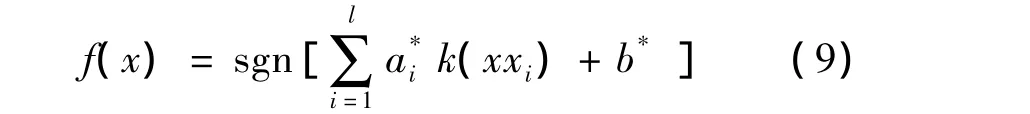
常见的核函数包括:线性核函数、径向基核函数、多项式核函数、sigmoid核等核函数，具体表达形式如表1所示。

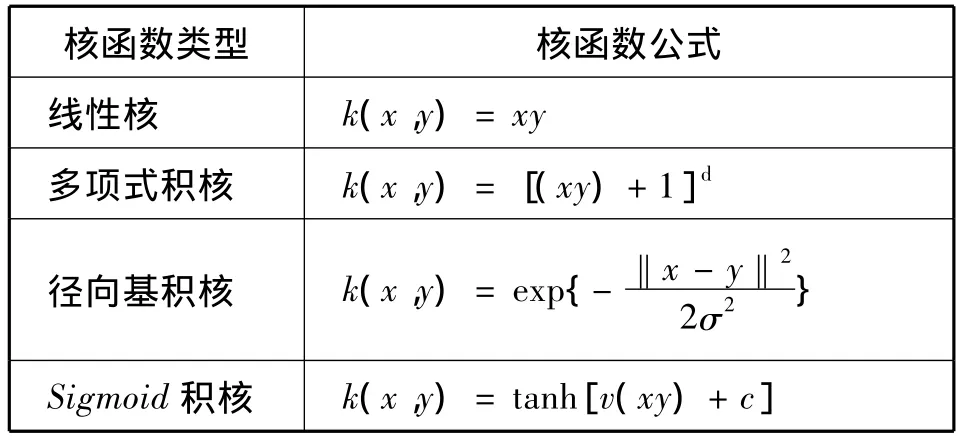
表1 核函数公式Tab.1 The nuclear function formula

3 利用圆谐矩与支持向量机的细胞识别

3.1 癌细胞介绍

癌细胞是一种变异的细胞，是产生癌症的根源。癌细胞来源于正常细胞，却又与正常细胞不同:

（1）癌细胞核可比正常细胞大数倍，并且细胞核的大小不等。

（2）细胞核畸形，核膜变形，并且癌细胞核染色质增多，使得细胞核颜色变深。

（3）核质比例失常，并且癌细胞分化愈差，核质比例失常愈明显，此外，细胞核染色质边移，出现巨大核仁，异常核分裂并出现梭形、蝌蚪形、星形等异常形态。

这些是癌细胞的一般特征，同时也是涂片辨识癌细胞的重要标准。

图3 正常细胞与癌变细胞Fig.3 The normal cells and cancerous cells

3.2 细胞图像识别的一般步骤

对于给定的细胞涂片显微图像，如果要计算机进行自动识别图像，一般需要如下几个步骤，即预处理，图像分割，特征提取，细胞识别。

首先，要对图像进行预处理。这样做的目的，一方面是去掉不必要的信息，另一方面是使图像的有用特征更加突出。

其次，对图像进行分割，提取需要识别的部分，为之后的识别做准备。由于提取出的细胞图像往往是成团成组出现的，其中的单个细胞往往会出现相互重叠的现象，因而将其分离开有较大的难度。现今的单个细胞分割分离方法中，主要是利用各种算法将细胞的边界大致的分离开，而后根据重叠部分的灰度数据，对细胞的边缘和灰度值进行估计与重建。

再次，需要对细胞进行分析，选取某些特征进行提取。在迄今的各种识别方法中，往往采取对正常细胞与癌细胞作比较，分析其中的不同点，例如癌细胞核较正常细胞核较大；各个癌细胞核大小不一，出现畸形；细胞外形不规则，出现凹陷、皱褶、锯齿状，或细胞膜边缘模糊不清，出现浸润现象等。针对这些外观上的明显不同点，提取不同的特征来为进一步的分类与识别做准备。

根据特征提取中提取出的细胞特征，使用各种分类方法，对分类器进行训练，以达到对未知样本的识别。

3.3 利用圆谐矩与支持向量机的细胞识别

对于给定的灰度图像f（x，y），由于圆谐傅里叶矩的计算公式为:

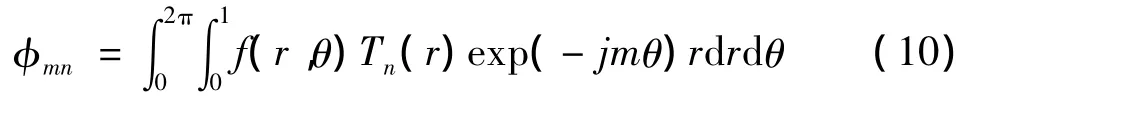
其中具有旋转因子exp（jmθ），使得在图像旋转任意角度φ后，得到的所有的矩都增加了相同的相位因子exp（jmθ），而其幅度大小，即模值||是不变的。于是对于圆谐-傅里叶矩来说，其本身公式结构便具有旋转不变性的性质。

而对于平移、灰度与尺度的不变性，圆谐-傅里叶矩并不是畸变不变量。因此，必须对其进行归一化，才能满足特征提取的要求。

在特征提取与图像识别过程中，由于矩阶数升高会使运算量呈指数增长，造成时间消耗也呈指数增长，因而考虑运算量的几何级增长，我们权衡运算量与图像描述能力，选定n=7为识别过程中的圆谐矩阶数。

本算法选用C-SVM来进行分类与识别，选用线性核进行分类识别，惩罚因子C的取值为1.

3.4 对识别算法的改进

在识别过程中，将训练样本集的样本数减少对识别效果影响并不大；而如果将训练样本集中加入或去掉某些特定图像，对识别效果具有很大的影响，往往可以使得识别准确率增减10%.

究其原因，是由于在细胞识别中，癌细胞较正常细胞具有细胞核较正常细胞核较大，细胞外形不规则，细胞膜边缘模糊不清，出现浸润现象等图像特点。如果样本集中图像具有这些特征，则尽管样本数量不多，却仍可以保证识别正确率。因此，对本算法的改进，便是如何寻找一种自动算法，使其能够自动将标准的细胞图像包含其中，将变形的细胞图像剔除。

本文采取的方法大致为:对训练集进行若干次再分割，将其随机分为训练集与测试集。用训练集样本对支持向量机进行训练，得到最优分类面，而后对测试集样本进行分类，得到对样本集中训练集的分类准确率。保留准确率高的最优分类面，去掉准确率低的。最后，用得到的几个最优分类面对测试集的样本进行分类，投票得出最后结果。

本文采用随机挑选划分的方法确定训练集中样本数量。随机从样本集中取数量为n的样本进行优化，得到最优分类面，对剩余的样本进行判别，得到准确率结果如表2所示。

表2 不同样本集规模的识别准确率Tab.2 The recognition accuracy of the sample set size

由表2结果可看出，在n≥8的时候，由于样本规模足以包含足够数量的支持向量，因而样本数量的提升对结果影响并不大。而在n≥14的时候，往往会包含个别变异图像，使得模型的识别准确率下降。

考虑训练集增加对识别率与时间消耗的影响，我们选择n=10为样本数，使训练集规模稍高于最低所需样本规模。

对不同阈值与不同最优分类面下的投票正确率进行理论分析，发现0.8为阈值可以兼顾准确率与最优分类面筛选个数，因此较为合适。

3.5 实验与分析

对以上结果进行实验，实验所用样本集正常图像为50幅，癌细胞图像50幅，测试集细胞图像50幅。

基于如上参数，本算法实现步骤如下:

（1）将样本集随机分为训练样本集与测试样本集，训练样本集中正常细胞与癌细胞各10个，其余为测试样本集。

（2）对训练样本集中图片进行7阶圆谐-傅里叶矩的计算，提取出一个64维的图像特征值，组成训练集:

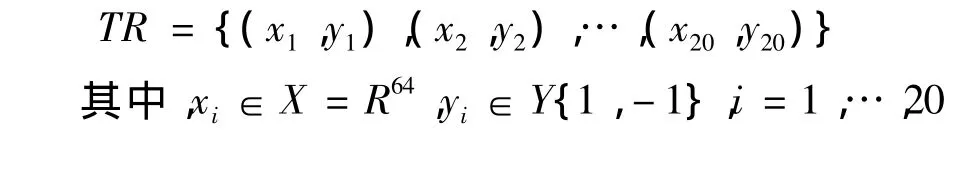
（3）对得到的特征向量使用C-SVM进行优化:

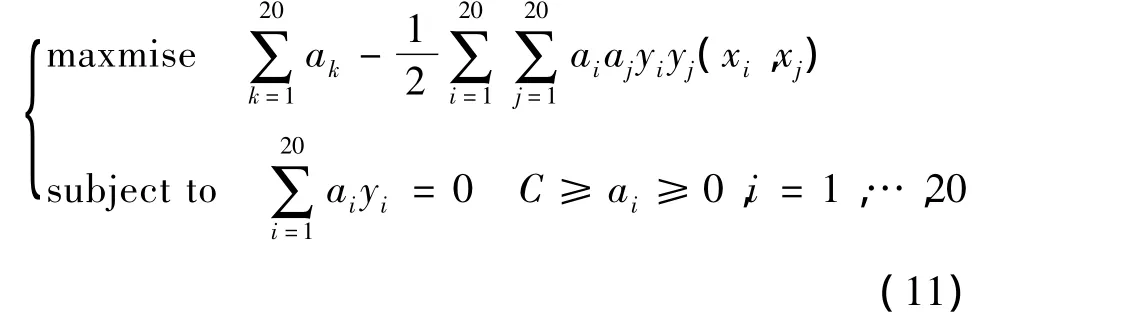
得到最优解a*=（，…）

（4）由最优解，得到:

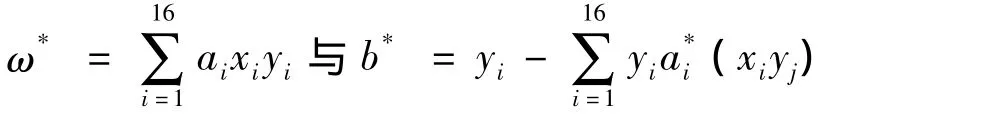
继而得到最优分类面:

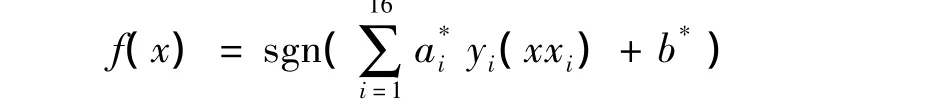
（5）同样对测试样本集中图片提取圆谐-傅里叶矩，使用得到的最优分类面对其进行分类，得到分类准确率，保留准确率高于80%的分类面。

（6）重复以上步骤，以得到多个最优分类面。

（7）使用得到的最优分类面对待识别图像进行识别，而后用识别结果进行投票，由投票结果得出最终识别结果。

为了证明选择圆谐-傅里叶矩的正确性，分别用圆谐-傅里叶矩与正交傅里叶-梅林矩相结合，对相同细胞图像进行识别。识别过程中都在支持向量机中选用线性核，且使C=1，得到结果如图4所示。

图4 正交傅里叶-梅林矩与圆谐-傅里叶矩识别时间对比图Fig.4 The recognition time comparison chart of orthogonal Fourier-Mellin moments and circular harmonic-Fourier moment

由此可看出，圆谐-傅里叶矩在识别速度上，优于正交傅里叶-梅林矩。

对圆谐-傅里叶矩与支持向量机算法结合，与对其改进后的算法比较，得到结果如表3所示。

由表3可看出，采用该改进算法后，可以使其使用低阶矩，取得未改进算法使用高阶矩所得到的识别率。而在阶数升高后，采用本改进算法可将识别效率提高8%左右。

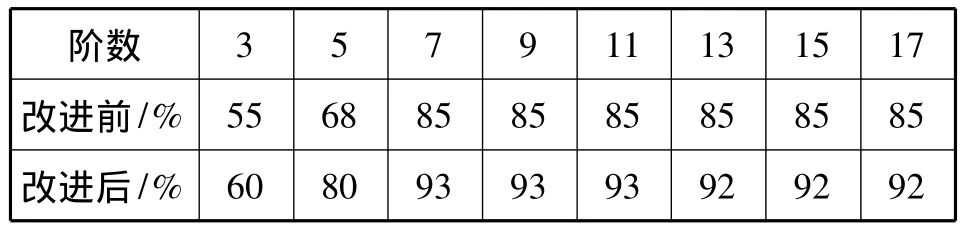
表3 改进前后准确率对比Tab.3 The improved accuracy before and after contrast

4 结论

由上述实验可看出，对于使用图像矩作为图像特征的识别算法中，圆谐-傅里叶矩具有运算效率高，描述效果好的优点。将圆谐-傅里叶矩与支持向量机相结合，能够使其运算速度方面的优势更为明显。而将该算法中的支持向量机进行一些改进，则可以在不提高阶数的情况下，提高识别的准确率，使识别时间没有太大变化。

［1］Al-HAJJ M，WICHA M S，Clarke MF.Prospective identification of tumorigenic breast cancer cells［J］.Proc Natl Acad Sci USA，2003，100:3983-3988.

［2］SINGH S K，BONN V E，HAWKINS C.Identification of a cancer stem cell in human brain tumors［J］.Cancer Res，2003，63:5821-5828.

［3］LI C，HEIDT D G，DALERBA P.Identification of pancreatic cancer stem cells［J］.Cancer Res，2007，67:1030-1037.

［4］LAM K M.Fast algorithm for locating head boundaries［J］.Electron Imag，1994，4（3）:352-359.

［5］WU R，SHENG Y.Image description with Chebyshev-Fourier moments［J］.Opt Soc Am A，2002，19（9）:1748-1754.

［6］HU M K.Visual pattern recognition by moment invariants［J］.IEEE Trans Inform Theory，1992，8（2）:179-187.

［7］PING Z L.Computation of orthogonal Fourier-Mellin moments in two coordinate systems［J］.Journal of Optical Society of America A，2009，26（5）:1080-1084.

［8］VAPNIK V.Statistical Learning Theory［M］.USA:John Wiley ＆ Sons，Inc，1998.

［9］KHOTANZAD A，HONG Y H.Invariant image recognition by Zernike moments［J］.IEEE Trans Pattern Anal Machine Intell，1990，12（4）:489-497.

［10］VAPNIK V.The support vector method of function estimation［J］.Advanced Black-Box Techniques，1998（5）:55-85.