一种改进的CPSO-BP神经网络故障诊断技术研究

2013-10-16董增寿张春梅

太原科技大学学报 2013年5期

王慧，董增寿，张春梅

（1.太原科技大学，太原 030024；2.新疆69028部队，乌鲁木齐 830006）

液压泵作为液压系统的心脏，液压泵故障将导致整个液压系统的瘫痪，这就使其成为动力系统故障诊断的关键［1］，因此有必要对液压系统进行实时的故障预报、监测和诊断，及早地发现故障，避免更大的经济损失。由于液压系统故障征兆与故障原因之间复杂的非线性映射关系，用传统的基于信号处理、数学模型的故障诊断技术很难进行实时准确的诊断。近年来由人工智能构成的故障诊断系统逐渐兴起，在实际应用中用神经网络构成智能故障诊断系统是比较常用的诊断模型。

BP网络是神经网络中常用的网络类型，它采用基于梯度下降法的学习方法，其收敛速度慢且易陷入局部极小值［1］。PSO算法是基于群体智能理论的优化算法，它不但具有全局寻优能力，而且通过调整参数还可以同时具有较强的局部寻优能力。常采用PSO算法对BP网络参数进行优化，且这种方法在故障诊断领域［2-5］有很好的研究应用。PSO算法存在的不足是，在寻优过程中种群多样性的丧失容易导致算法出现早期收敛的现象。为了避免这种现象的出现，主要有对收敛因子w的改进［4，6］、用遗传算法的交叉变异对速度进行调节［5］，但遗传算法的引入无疑又会增加PSO算法的复杂度。文中在对惯性权重w进行改进的基础上利用混沌运动具有遍历性、随机性和规律性的特点［7-9］来对PSO算法的各参数进行调节，构成CPSO算法，并用该算法来优化BP网络，就柱塞泵的常见故障构建CPSO-BP神经网络。之后与只进行惯性权重w改进的PSO-BP网络进行比较，实验结果表明CPSOBP网络在收敛率及诊断精度上都取得了较好的效果。

1 粒子群优化（PSO）算法

1.1 标准粒子群优化算法

标准粒子群优化（particle swarm optimizaton，PSO）算法采用速度-位置搜索模型［10-12］。每个粒子代表解空间的一个候选解，解的优劣程度由适应度函数决定，适应度函数根据优化目标函数确定。粒子i在d维解空间的位置为xi（xi1，xi2，…，xid），速度vi（vi1，vi2，…，vid）决定粒子在搜索空间单次迭代的移动方向及位移大小。标准PSO算法将解空间随机初始化为取值范围内的一群粒子。每一次迭代，粒子通过动态跟踪自身的最优解pi（pi1，pi2，…，pid）及整个种群的最优解 gi（gi1，gi2，…，gid）来更新自身速度和位置。它是通过群体之间的资源共享和个体自身总结来修正个体行动策略，最终求取优化问题的。粒子i的速度与位置更新公式分别为公式（1）和公式（2）:

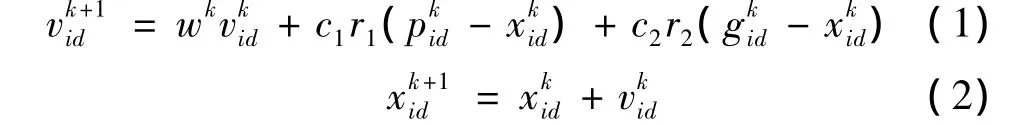
其中wk为惯性权重系数；c1、c2为学习因子；r1、r2为分布在［0，1］之间的随机数；i=1，2，…，m，m群体中粒子总数为第k次迭代粒子i搜索速度向量的第d维分量，粒子在每一维搜索的速度不能超过算法设定的最大速度vmax；为第k次迭代粒子i位置向量的第d维分量为粒子i个体最好位置的第d维分量；为群体最好位置的d维分量。

标准PSO算法搜索过程存在的不足有:

1）随机的初始化过程，使解群中个体的质量不能得到很好的保证，这样就会降低最终解的质量及求解速度；

2）粒子的速度更新公式（1）中，wk固定，r1、r2为［0，1］之间的随机数，无法保证对解群遍历完整性；

3）容易陷入局部最优解。

1.2 混沌粒子群优化（CPSO）算法

混沌［10-12］是自然界广泛存在的一种非线性现象，目前对它尚无严格的定义，一般将由确定性方程得到的具有随机性的运动状态称为混沌。Logistic映射就是一个典型的混沌系统，其迭代公式为:

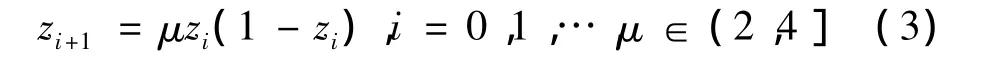
式中:μ为控制参量，当μ=4，0≤z0≤1时，Logistic完全处于混沌状态。利用混沌运动的特性可以进行优化搜索，其基本思想是首先产生一组与优化变量相同数目的混沌变量，用类似载波的方式将混沌引入优化变量，使其呈现混沌状态，然后利用混沌变量具有遍历性、随机性和规律性的特点进行搜索。初值不包括混沌迭代方程的4个不动点（zi=0.00，0.25，0.75，1.00）.

本文将利用μ=4时的混沌运动特性来改进标准粒子群算法。取公式（3）的Logistic映射为混沌信号发生器，公式如下:

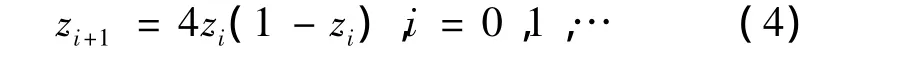
在初始化粒子群阶段利用混沌运动的遍历性，利用公式（4）产生出优良的初始群体作为初始粒子群，这样就可以减轻随机初始化粒子群对算法优化性能的影响。

在标准PSO算法中，对参数wk、r1和r2的设计，通常是wk固定为某个值，r1和r2取为［0，1］间的随机数，从公式（1）可看出这些参数对算法收敛效果与遍历完整性有明显影响。为了增强参数的调节能力，获取更好的全局搜索能力，提高算法搜索精度，文中对wk、r1和r2用混沌运动进行调节，按照公式（5）及公式（6）进行，公式如下:

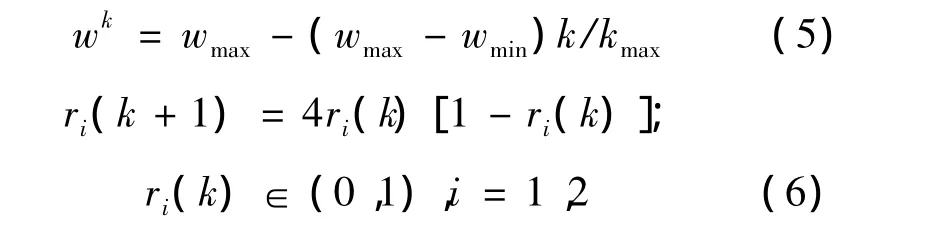
采用2个常用的测试函数做仿真实验来测试混沌粒子群优化（CPSO）算法的性能。所用测试函数如下:

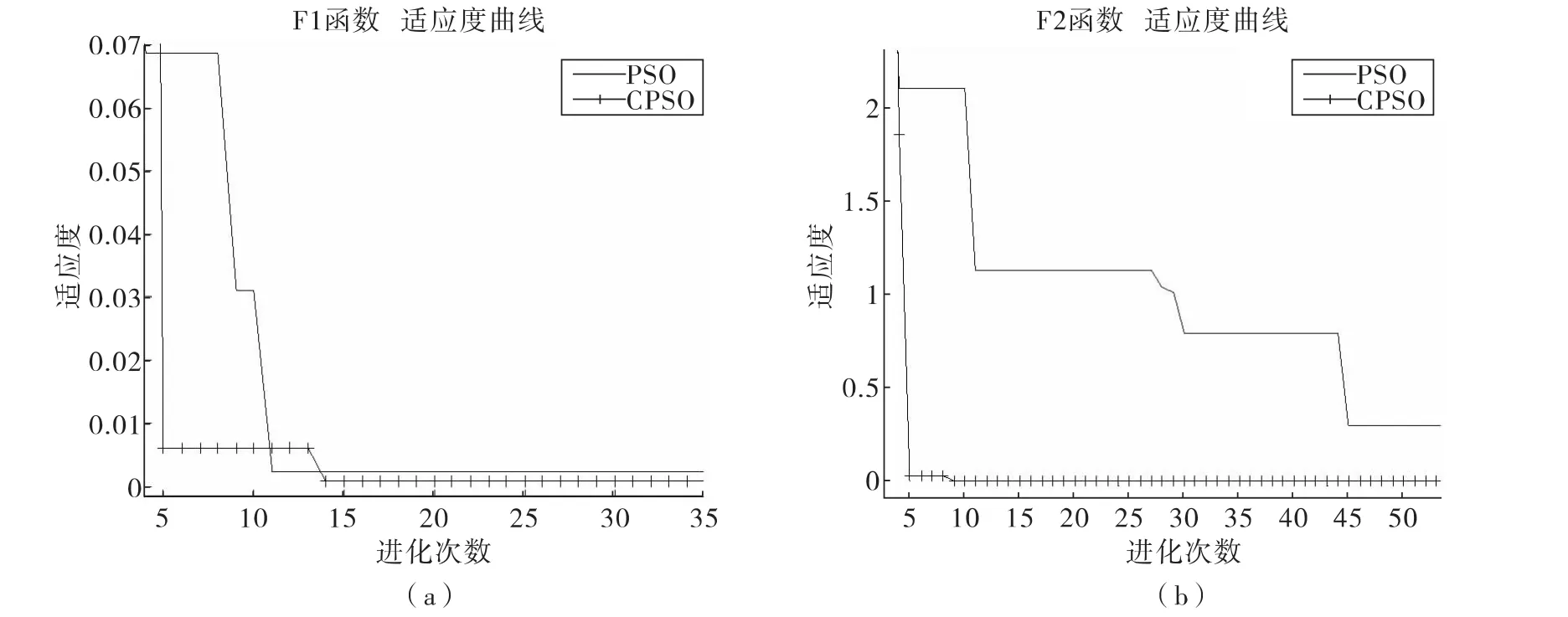
图1 收敛速度比较图Fig.1 The contrast chart of onvergence speed

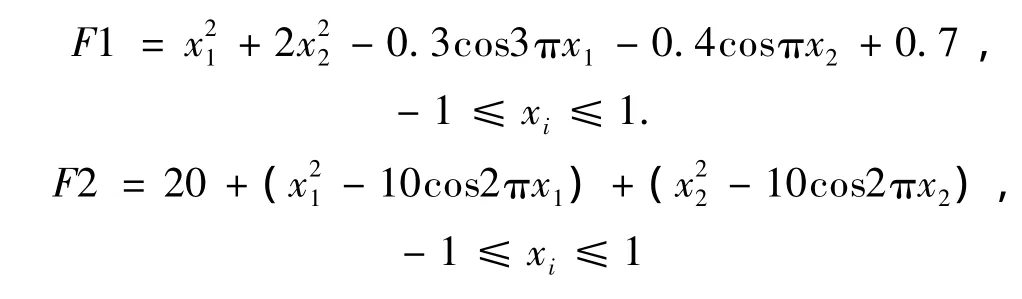
仿真结果图如图1所示，图1（a）为分别用标准PSO算法、CPSO算法对F1函数仿真的比较图，图1（b）为分别用标准PSO算法、CPSO算法对F2函数仿真的比较图。

经过仿真计算证实该算法不仅保持了PSO算法结构简单的优点，而且又具有混沌运动搜索速度快、计算精度高、易跳出局部极小的特点。对PSO算法存在的计算精度不高、易陷入极小值的缺点均有很大的改进。

2 CPSO-BP网络

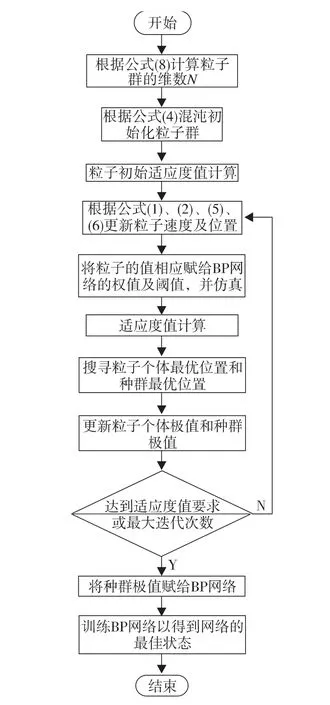
图2 CPSO-BP算法流程图Fig.2 The CPSO-BP algorithm flow chart

BP算法采用梯度下降学习算法，其权值的修正是沿着误差性能函数梯度的反方向进行的［13］，这种算法在对神经网络训练时容易陷入局部极小值，收敛率也较低，因此论文采用CPSO算法优化BP网络。

CPSO算法优化的目标是BP算法各层神经元的权值和阈值，以均方误差作为粒子的适应度函数，如公式（6）所示:

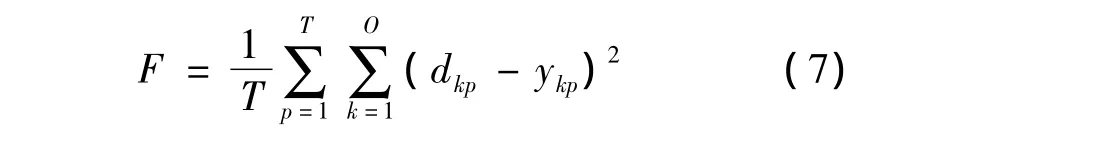
式中T为样本个数，O为输出层神经元个数，dkp为节点的期望输出，ykp为节点的实际输出。

文中采用三层结构的BP网络，令R、S1、S2分别为输入层、隐含层、输出层神经元的个数，则粒子群个体位置向量P的维数N与BP网络的权值和阀值关系如公式（7）所示［14］:

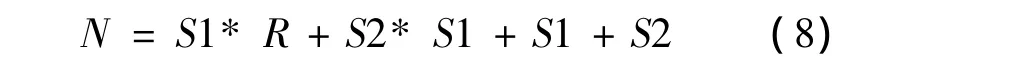
CPSO-BP算法的设计流程图如图2所示。

该算法将经过CPSO算法寻优得到的值赋给BP网络的权值及阈值，作为BP网络训练的初始值，减少了随机初始化过程对BP网络训练的影响，之后BP网络再用自身算法进行训练，这样就可以在极短的训练次数内完成网络训练，且可以提高网络的收敛率及诊断精度。

3 柱塞泵故障诊断仿真

采集柱塞泵正常工作和球头松动、松靴、配流盘磨损、缸体磨损、轴承磨损和泄露故障时垂直方向的振动信号构造网络。实验所用数据采用文献［1］中提供的数据，如表1所示为对振动信号进行特征提取并归一化处理后的数据，故障模式如表2所示。BP神经网络选取8-10-6的结构，对上述7种状态进行故障诊断。选CPSO算法的粒子群数为20，根据公式（7）可知粒子维数N为N=10×8+6×10+10+6=156.按公式（4）混沌初始化粒子群，学习因子 c1、c2设为 1.4945，r1、r2按照公式（5）及（6）进行设置。

如图3所示，分别为BP网络、只改进w的PSOBP网络及CPSO-BP网络仿真图。

表3为PSO=BP网络及CPSO-BP网络的实际输出值。

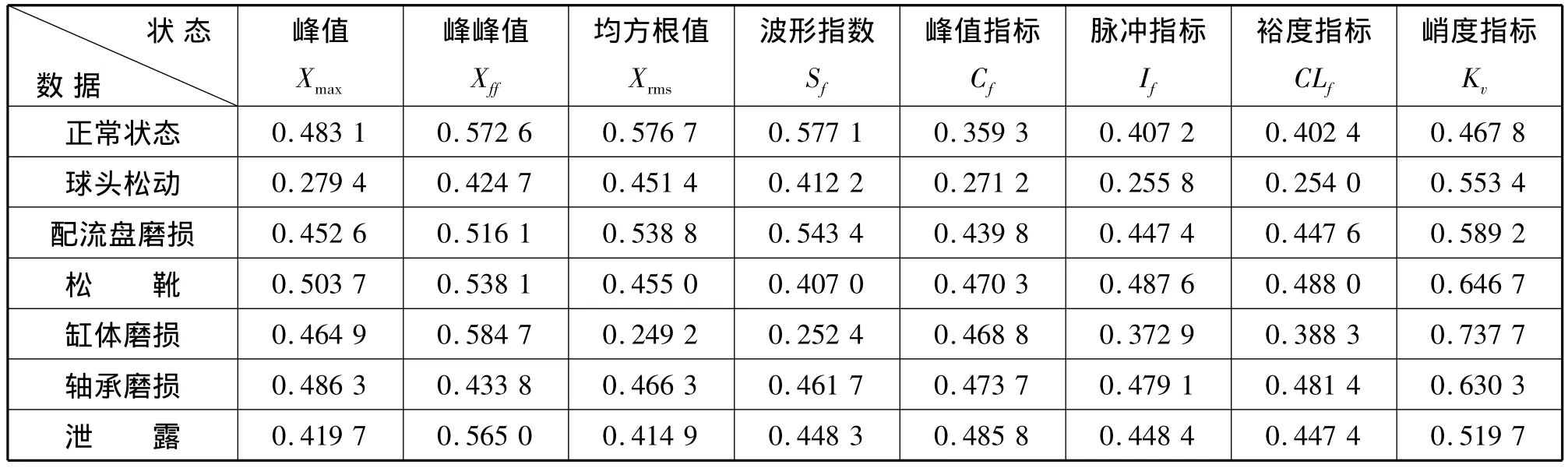
表1 柱塞泵垂直方向故障数据表Tab.1 The data table of the pump fault in vertical dir ection

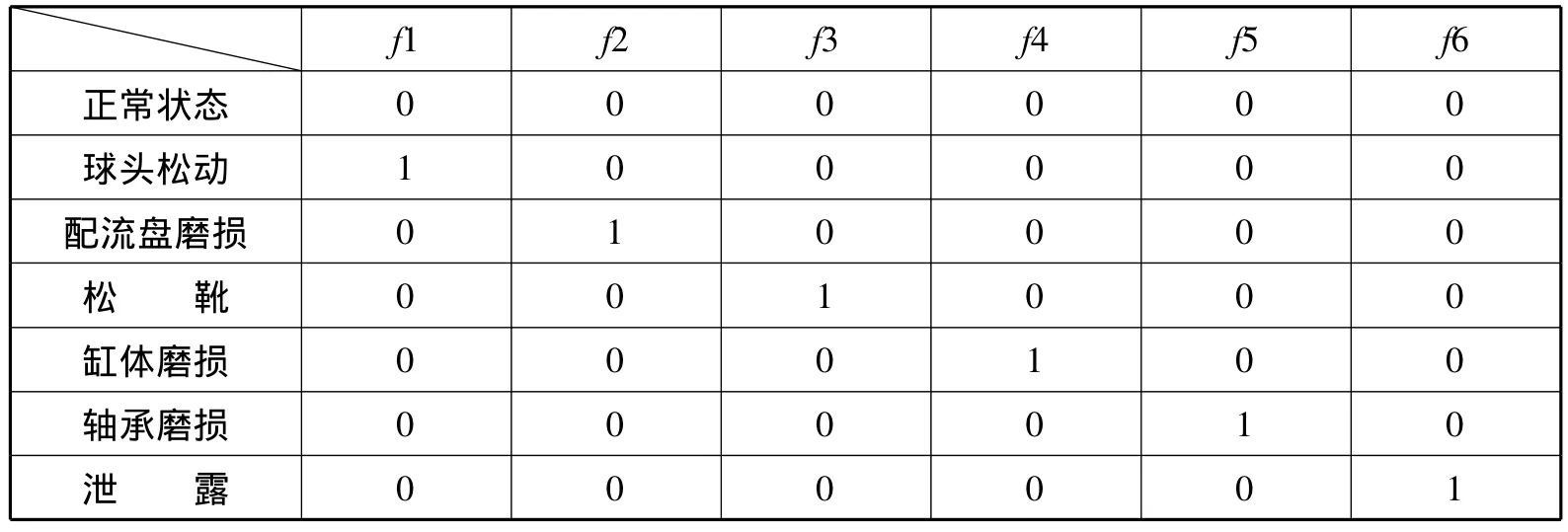
表2 故障模式表Tab.2 The fault mode table

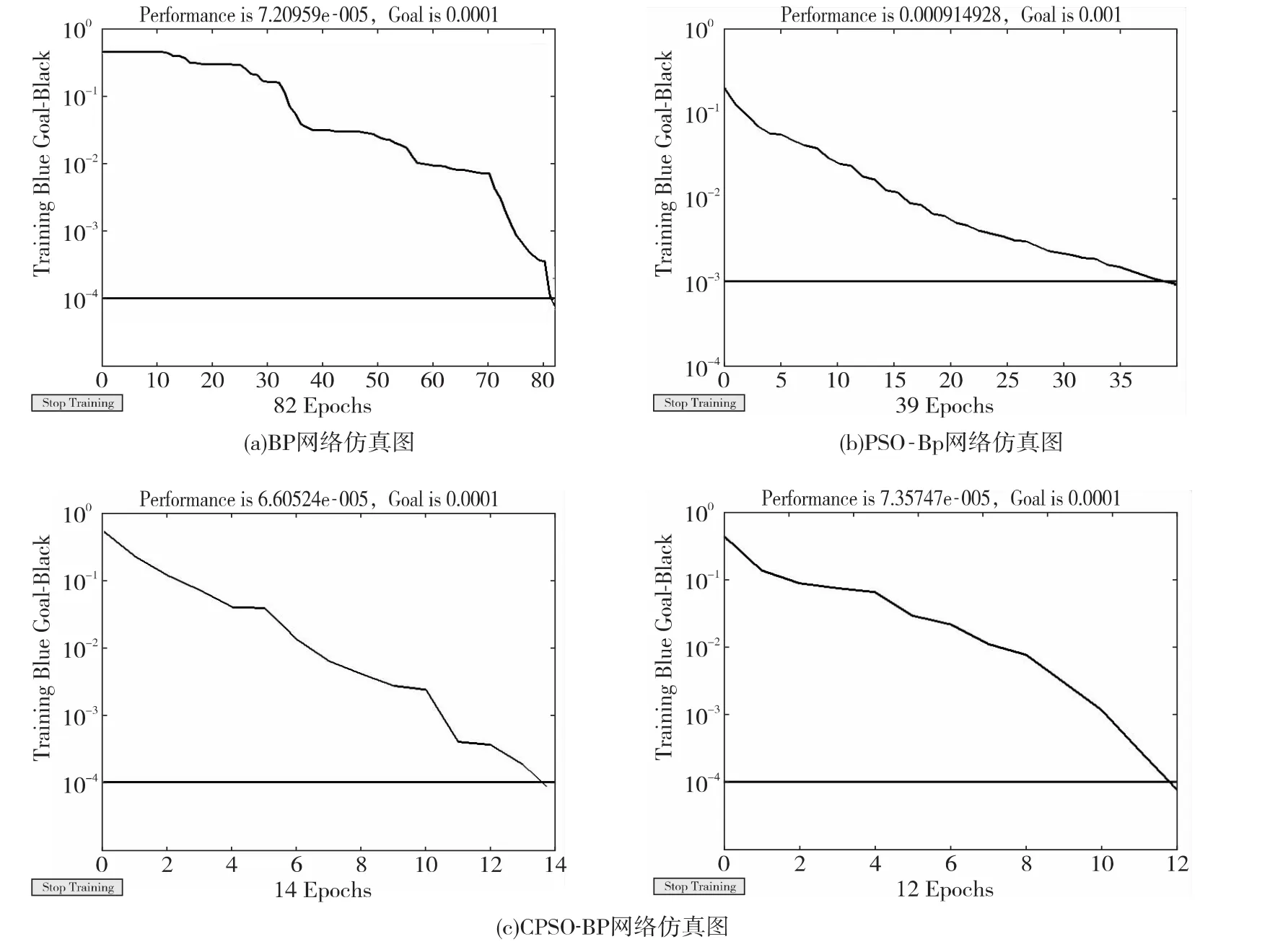
图3 仿真图比较Fig.3 The comparison of simulation chart

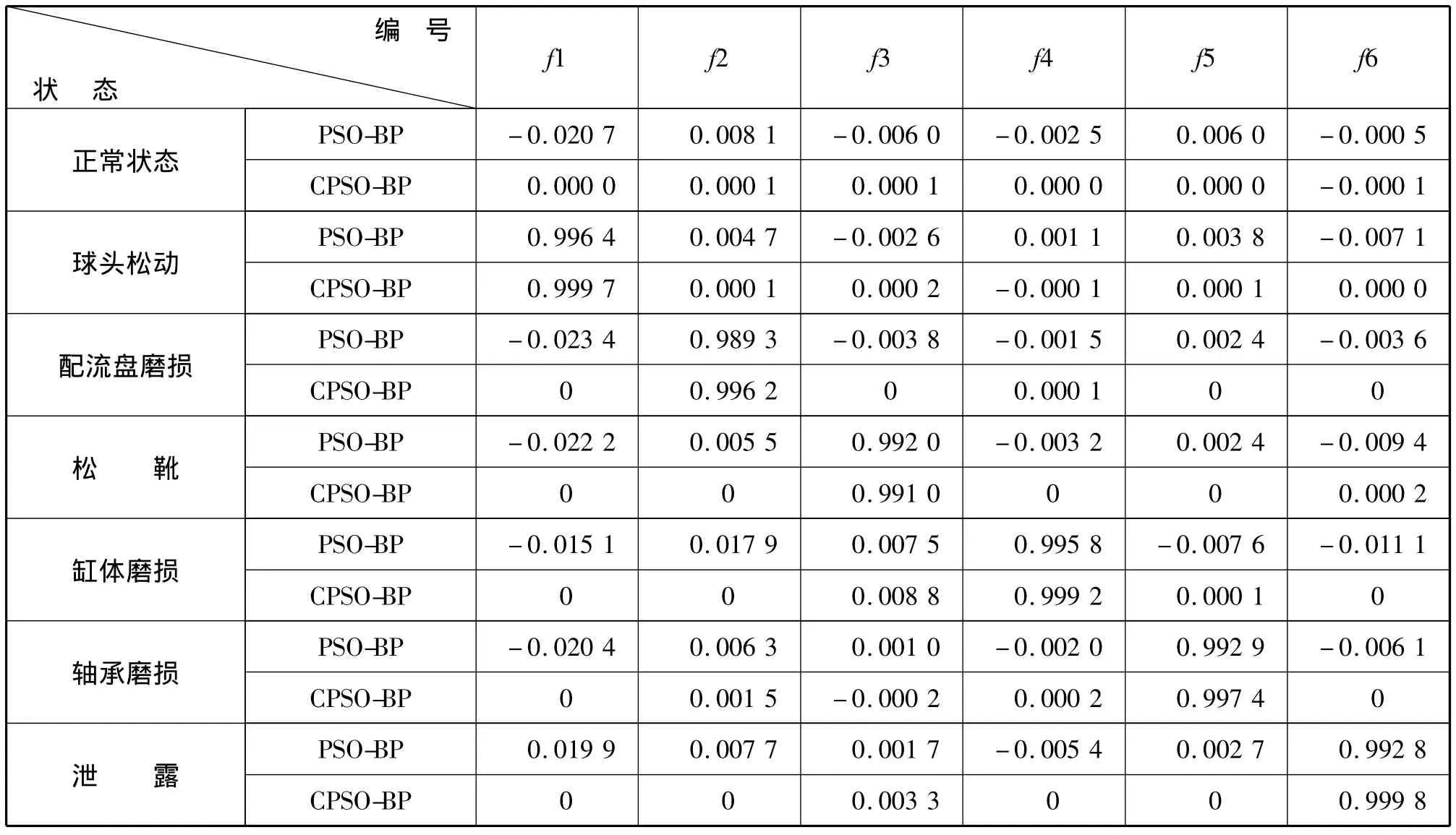
表3 PSO-BP与CPSO-BP网络输出值比较Tab.3 The comparison of output values of PSO-BP and CPSO-BP network

4 结论

比较图2中的4条曲线，可以看出CPSO-BP网络训练次数明显少于前两种，收敛速度得到很大的提高，并且从表3可以看它的实际输出值更稳定，更接近于期望输出值。实验表明用CPSO-BP网络进行柱塞泵的故障诊断，其实际输出更精确，诊断结果更有效、可靠。

［1］饶泓.基于多源信息融合与Rough集理论的液压机故障诊断方法研究［D］.南昌:南昌大学，2009.

［2］SUN HUIQIN，XUE ZHIHONG，SUN KEJUN.Fault Diagnosis Analysis of Power Transformer Based on PSO-BP Algorithm［C］∥International Conference on Intelligent System and Applied Material（GSAM），Xi'an，China，2012.

［3］冯辉宗，吴小敏，袁荣棣，等.基于PSO-BP神经网络的发动机故障诊断［J］.化工自动化及仪表，2013，40（1）:76-79.

［4］段向军，韩满林.改进PSO-BP网络在故障诊断中的应用［J］.机床与液压，2011，39（1）:138-140.

［5］李晓豁，张景晖.连续采煤机运煤系统智能故障诊断［J］.机械设计与研究，2009，25（3）:114-116.

［6］张晓宇.一种改进的PSO-BP算法在液压系统故障诊断中的应用［J］.液压气动与密封，2012，32（11）:13-18.

［7］杨俊杰，周建中，喻菁，等.基于混沌搜索的粒子群优化算法［J］.计算机工程与应用，2005，16:69-71.

［8］赵志学，罗可，唐江桦.改进混沌PSO算法的电力系统最优潮流计算［J］.计算机工程与应用，2009，45（25）:205-207.

［9］李莉.基于自适应参数与混沌搜索的PSO算法求解柔性作业车间调度问题［J］.计算机应用，2012，32（7）:1932-1934，1950.

［10］杜荣华.一种促进PSO全局收敛的参数调整策略［J］.系统工程与电子技术，2009，31（6）:1454-1457.

［11］周驰，高海兵，高亮，等.粒子群优化算法［J］.计算机应用研究，2003，20（12）:7-11.

［12］陈国初，俞金寿.微粒群优化算法［J］.信息与控制，2005，34（3）:318-324.

［13］周开利，康耀红.神经网络模型及其MATLAB仿真程序设计［M］.北京:清华大学出版社，2005.

［14］黄继红.基于改进PSO的BP网络的研究及应用［D］.长沙:长沙理工大学，2008.