基于虚拟材料的结合面建模与参数获取方法
2013-10-16贾文锋张学良温淑花陈永会
贾文锋,张学良,温淑花,陈永会,杨 波
(太原科技大学机械工程学院,太原 030024)
机床为了满足各种功能与性能要求,一般都不是连续的整体,进而导致了结构问题的复杂性,这是由于结合部中存在着接触刚度和接触阻尼[1]。随着机床高速、大载荷、高精度要求的不断提高,人们对机械结合面建模及参数识别方法越来越予以重视,并提出了一些方法与应用[2-3],但一般传统建模及参数识别方法得到的结合面刚度、阻尼数据难以直接应用于实际工程,且刚度、阻尼不像弹性模量、泊松比、密度等能表示材料固有特性那样来表示结合面的属性。因此,进一步进行结合面建模的研究将对机床结构整机高精度动力学建模具有重要意义。
基于此,本文提出基于虚拟材料的结合面建模方法,该方法利用结合面元单元接触刚度矩阵与虚拟材料的实体单元刚度矩阵之间的等效原则获得虚拟材料的固有的特性参数,并用这些参数来代替传统建模及参数识别的结合面的特性参数,从而能方便实现实验数据的工程应用。
1 基本思路
结合部是由两个子结构厚度很小的接触表层构成的,从理论上可以将其等效成某种厚很小的虚拟材料,且假定该虚拟材料分别与两子结构之间是固定连接。如图1所示,其中图1(a)是由两个子结构连接构成的结构,中间部分是相互接触部分即结合部,图1(b)是基于这种思想的等效结果,C即是具有一定厚度的虚拟材料。
在对图1(a)的结构进行有限元划分时,两个子结构在结合面处所划分的单元数目和大小应对应相同且位移模式相同,根据文献[4]提出的结合面元法可以建立其无阻尼自由振动的动力学方程为:
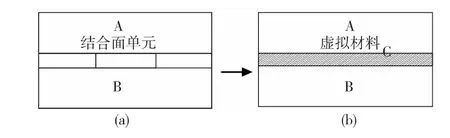
图1 结合面示意图Fig.1 The diagram of the joint surfaces
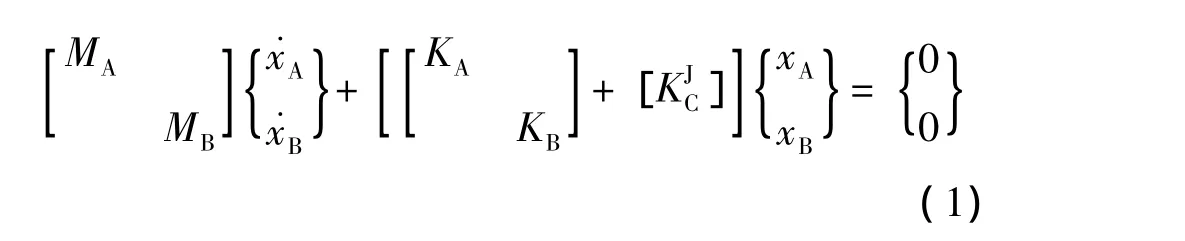
对图1(b),应用有限元方法可以建立其无阻尼自由振动的动力学方程为:
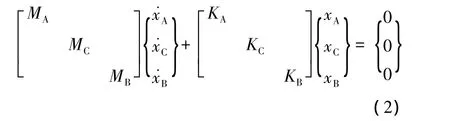
由于假设的虚拟材料层的厚度非常薄(远远小于零件的尺寸),则C部分的质量可以忽略即:Mc=0.同样因为虚拟材料部分的厚度非常小,在进行有限元单元体划分时可以将其划分为单层。通过对(式(2))位移矩阵和刚度矩阵的观察发现,在进行总质量和总刚度方程的组装时,虚拟材料C部分的上节点和相应的自由度,包含在A部分与其相接节点上,其下节点和相应的自由度包含在B部分与其相接的节点上。这样式(2)中并没有出现新的节点和自由度,而仅仅是结构对应节点的矩阵的叠加。将式子(2)按结构的对应节点叠加形式得到如下方程:
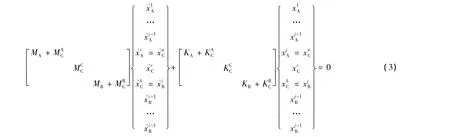
将式(3)简化为:
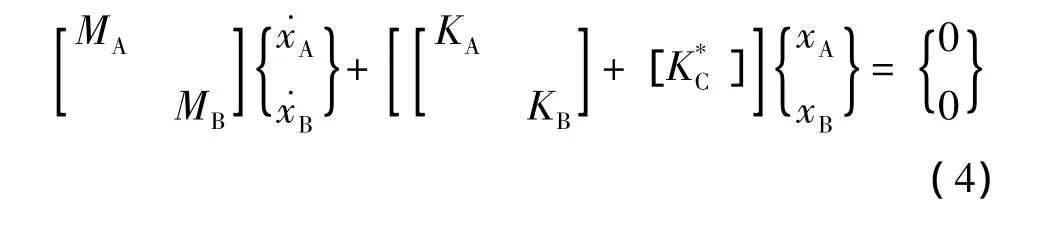
对式(1)与式(4)的比较发现,要使应用结合面元法建立的含有结合面的结构动力学模型与应用有限元法建立的含有结合面的结构动力学模型等效,需将结合面部分的刚度矩阵等效,即[]=[].
应用结合面元法,得到结合面元的单元接触刚度矩阵为[4]:
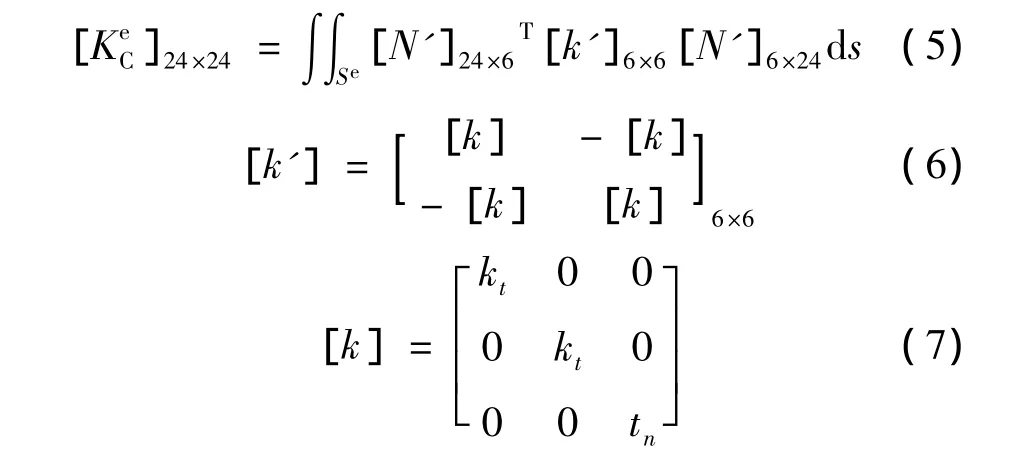
其中,kn,kt为结合单元相对节点法向和切向接触刚度。
应用8节点且每个节点3自由度的长方体实体单元来对结合面等效虚拟材料进行有限元计算,得到其单元刚度矩阵为[5]:
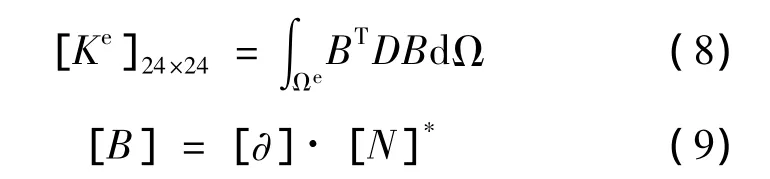
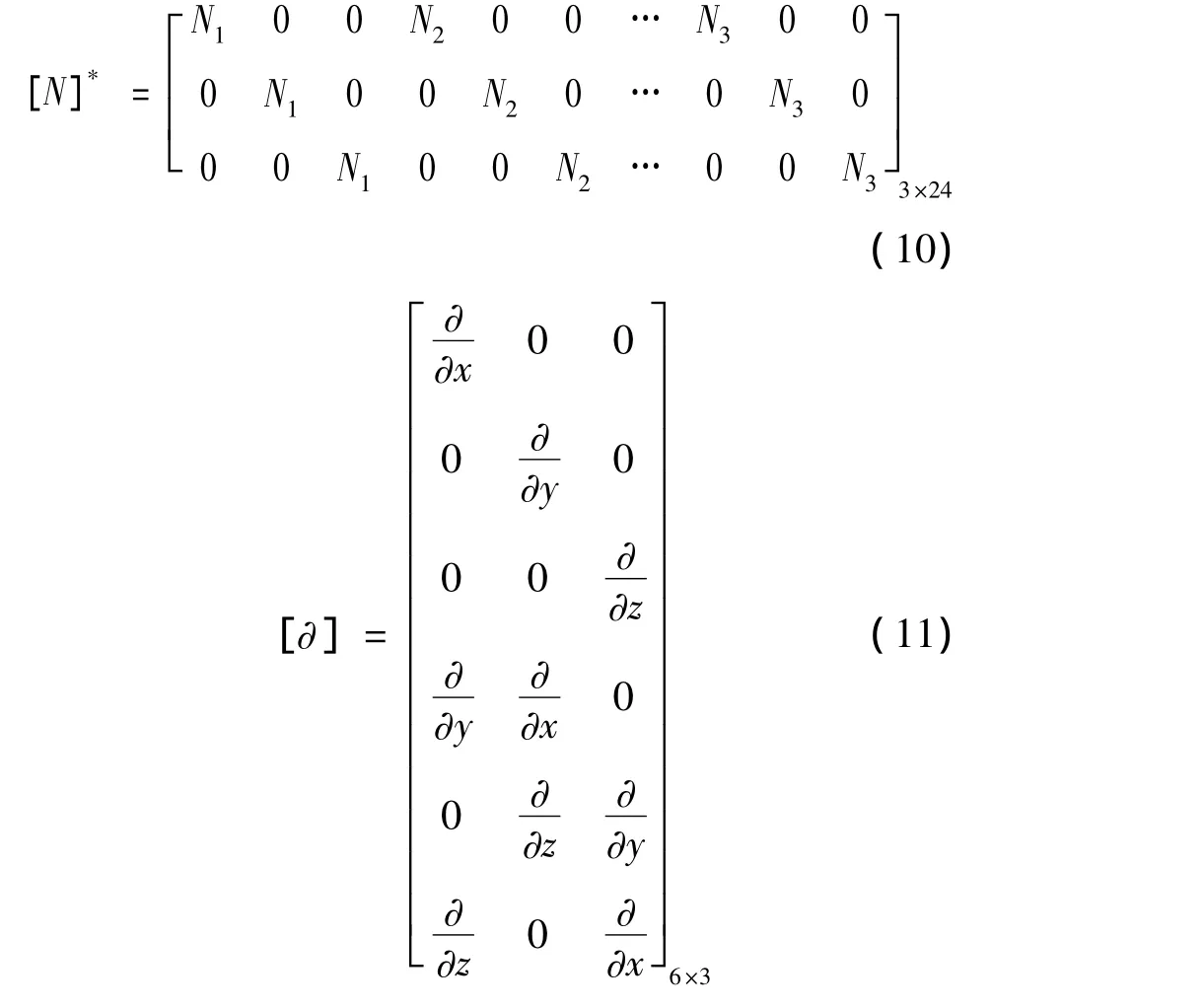
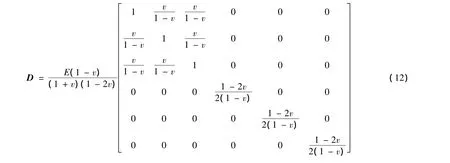
其中,E、v分别为结合面虚拟材料的弹性模量与泊松比。
利用结合面元法建模与组合结构实验测试相结合的方法获得了一定的结合面接触刚度数据,但发现这些数据在工程实际应用中却比较困难,主要是结合面元法与有限元建模之间存在差异,无法直接衔接,从而难以直接应用。为解决之,采用上述方法,通过[KeC]与[Ke]的等效,获得结合面虚拟材料的弹性模量与泊松比,而虚拟材料的密度以及其他参数可以采用下述方法确定。
2 虚拟材料参数选择
2.1 虚拟垫片厚度的设定
综合考虑机械加工表面层的实际厚度范围[6]以及提高有限元计算精度,通过多次反复试算,将虚拟材料层厚度设定为0.5 mm较为合理。
2.2 虚拟材料密度的设定
虚拟材料是结合面子结构两个表面层组成等效形式,根据密度的定义[7-8]:
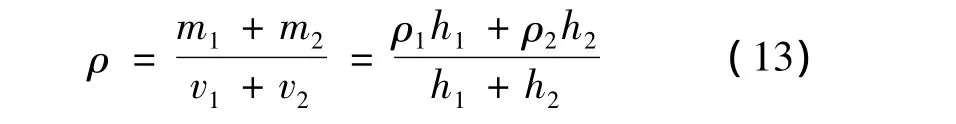
式中,m1,m2表示两表面层的质量,ρ1,ρ2表示表示两子结构的密度,h1,h2表示两表面层的厚度,经过对零件表层结构对比分析,取h1=h2,由此可以得到ρ=,即虚拟材料的密度为两个子结构密度的平均值。
2.3 虚拟材料单元体尺寸的设定
经过一定量的数据计算表明,单元尺寸的大小对最终识别出的参数E,υ的影响较小,在实际计算中为了减小数值计算过程中的误差,将单元尺寸设定在与虚拟材料厚度相差不大的数量级上一般不超过102,以减小截断误差。
3 实例分析
借用文献[9]中的实验模型来评价本论文所提出方法的有效与可行性。实验模型如图2所示,实验试件材料属性及接触表面的相关参数如表1所示,结合面预紧面压为31.25 MPa.
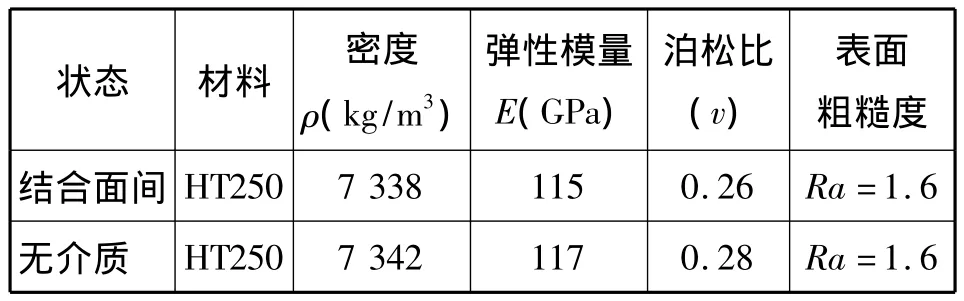
表1 两组合件的材料特性参数Tab.1 Parameters of surfaces
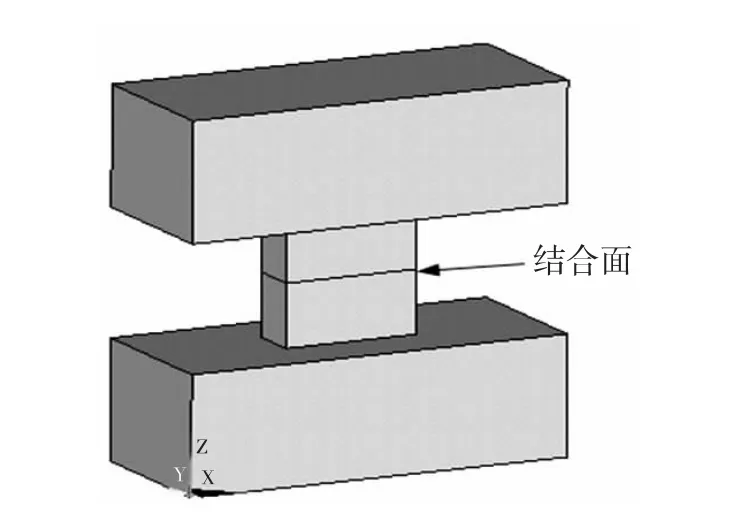
图2 实验模型Fig.2 Sample model
根据上述理论及实验数据可以得到相应的虚拟材料特性常数,并运用ANSYS建立有限元模型,在实验振型与结合面虚拟材料建模获得的理论振型相对应基础上得出结构的固有频率,其结果如表2所示,从中可以看出,基于虚拟材料的结合面建模方法及其基本参数的等效获取方法是可行的。
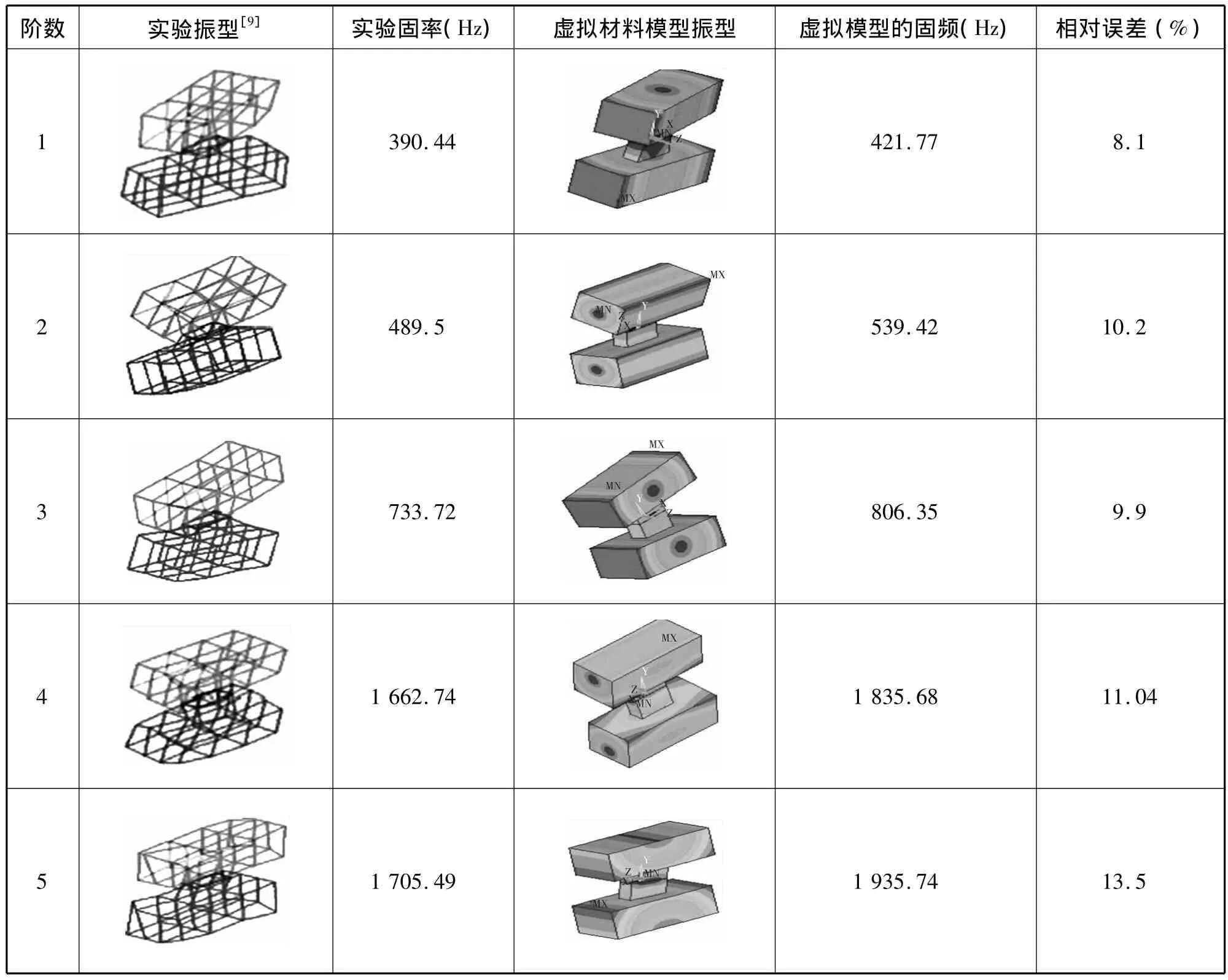
表2 模型的模态参数对比Tab.2 Comparison of modal parameters

4 结论
提出一种新的基于虚拟材料的结合面建模方法,并通过两种单元矩阵等效的方法获取了虚拟材料模型的特性常数,通过对实例的比较分析,不仅证明该虚拟材料模型和虚拟材料模型特性参数获取方法的的有效性,也表明了用模型参数等效表示难于直接运用实际结合面刚度、阻尼数据可行性。
[1]张学良.机械结合面动态特性及应用[M].北京:中国科技出版社,2002.
[2]INAMURA T,SATA T.Stiffness and damping identification of the element of a Machine Tool Structure[J].Annals of the CIRP,1979,28(1):235-239.
[3]廖伯瑜,廖永宜.机床结构建模的研究与应用[J].振动工程学报,1990,4(3):83-89.
[4]张杰,童忠钫.机械固定结合面动力学建模问题[J].振动与冲击,1994,51(3):16-22.
[5]曾攀.有限元分析及应用[M].北京:清华大学出版社,2004.
[6]温诗铸.摩擦学原理[M].北京:清华大学出版社,1987.
[7]田洪亮.机械结构固定结合部动力学建模[D].武汉:华中科技大学,2011.
[8]FISHKIS M,LIN J C.Formation and Evolution of a Subsurface Layer in a Metalworking Process[J].Wear,1997,206(1-2):156-170.
[9]田洪亮,朱大林,秦红玲,等.结合部法向载荷解析解修正与定量实验验证[J].农业机械学报,2011,42(9):213-218.
