K-S检验下的copula分布估计算法边缘分布的研究

赵 慧，王丽芳，介 婧，刘 洁

（1.太原科技大学复杂系统与计算智能实验室，太原 030024；2.浙江工业大学计算机科学与技术学院，杭州 310023）

分布估计算法［1］是一种新的种群进化模式，在遗传算法的基础上发展起来的，它不含有遗传算法的交叉和变异操作，而是从概率统计的观点出发，从当前优势群体提取信息建立概率模型，然后对概率模型随机采样产生新的解，如此反复进行，实现种群的不断进化，直到满足终止条件算法停止。随着分布估计算法的发展，对于大规模群体的计算相当复杂与不精确，因此现阶段的分布估计算法结合copula理论，解决了分布估计算法存在的问题［2］，这种将copula理论应用到分布估计算法中的方法就是基于 copula理论的分布估计算法（copula EDA）［3-4］。

在 copula 理论［3，5］中起重要作用的关键定理是Sklar定理。该定理表明:多变量的联合分布可以分解成两部分:边缘分布函数部分和copula函数部分。随着问题规模的增大，采用这种分而治之的方法，可以减少工作量，使问题简单化。表示联合分布只需要估计出各维变量的边缘分布函数，用copula函数将各维的边缘分布进行相应的连接即可，显然对各维变量的边缘分布进行估计和采样要比计算联合分布简单的多。Copula EDA独创之处在于，它既发挥了copula理论与分布估计算法两部分的长处，又弥补了分布估计算法单方面的不足，但是只有当两部分的选取都比较合适时才能达到很好的效果。

本文通过选取clayton copula为连接函数，对于边缘分布函数只采用一种分布函数（正态分布函数或者柯西分布函数以及构造经验分布函数）而言，这种直接选取某一分布函数作为边缘分布函数的原则忽略了样本分布的随机性与多样性。因此，本文将K-S检验［6］的思想应用到 copula EDA中（即基于K-S检验的copula EDA）的边缘分布函数部分，以充分考虑实际样本点的分布情况为前提，将柯西分布、t分布、正态分布等多种不同分布函数作为候选的边缘分布函数，进而采用K-S检验来判断各维的真实分布情况，每维变量都有自身所服从的分布函数，若不服从任何所假设的边缘分布，则构造各维相应的经验分布函数。这种算法能够增加种群多样性，改善执行效率。通过仿真实验，此算法具有更好的最优值而且能很快的收敛到最优值，后期种群也具有相对稳定性。

1 K-S检验的思想

本文用到的检验方法是K-S检验［7-8］，理由如下:

对于确定边缘分布部分，常用的方法除了从一些理论方面直接得到分布函数模型外，更多的是根据仿真和试验数据建立其相应的概率模型，进行有机的融合，即对其做服从某种分布的假设检验，通常采用的是经验分布EDF型检验、皮尔逊χ2检验和K-S检验等有效的假设检验方法来检验建模假设的正确性。分析检验方法:χ2检验针对的是离散分布，观察频数与期望频数差异作为检验指标，通常是大容量样本，而对于连续性总体研究时，则需离散化，那么有用信息就会损失，检验功效较差，因此对于连续性总体的检验，χ2检验并不是理想的检验方法。因此对于连续性分布可用EDF检验和KS检验，EDF检验是判断经验分布与假设分布之间的差异，适用于小样本，大样本时计算很复杂。而K-S检验是寻找实际分布与理论分布之间的最大距离，适用于大样本。因此经过分析我们可以采用KS检验来检验建模假设的正确性。

对于K-S检验的定义如下:

定义是K-S检验是检验样本是不是服从假设的理论分布函数的方法。

检验方法是以样本数据的实际累计分布与假设的理论分布比较，计算两个值的大小，若差值的绝对值在规定的范围内，则认为该样本服从或者近似服从该假设分布。

例如:H1表示样本值服从某假设的理论分，H2表示样本不服从某假设的理论分布。

令F1（x）表示预先假设的理论分布，F2（x）表示样本的实际累计概率分布，设D=max|F1（x）-F2（x）|.当 D ＞ D（n，a）［D（n，a）是显著性水平为a且样本容量为n时的拒绝临界值（查表可得）］，则拒绝H1，反之则接受H2假设。

2 基于K-S检验的copula EDA

2.1 K-S检验的应用

将K-S检验应用到copula EDA，其实只是运用在copula EDA的边缘分布函数选取部分。本文选择clayton copula函数作为连接函数，候选的边缘分布为柯西分布、t分布和正态分布等K种分布函数。在copula EDA基础上添加K-S检验，是因为这是一种根据实际样本点的分布情况和K-S检验来验证所服从具体分布函数的思想，而不是直接将各维的边缘分布函数确定为某一特定分布，由此各维变量的分布情况也许相同也许不同，视K-S检验的情况而定。因此具有一定的真实性和灵活性。

本文应用K-S检验，当样本数N为2000时，对10维的变量进行K-S检验，验证所假设的分布。检验时，根据优势群体的各维变量分别计算其统计量D1-D10，分别把样本分布的统计量和假设的分布相比较，比较得出实际的显著性水平p（0＜p＜1）来确定是否服从和近似服从假设的分布。若取得的p值小于给定的显著性水平a（其中a值通常取0.05，也可以适当的减小），则认为样本不服从所假设的分布，反之则认为样本服从假设分布。例如:利用K-S检验来检验某一维样本的正态性。首先，根据样本值计算其检验统计量D，把它的实际统计量理论的正态分布相比较得出一个数值p，若p值小于规定的显著性水平，则认为该样本不是服从正态分布。反之则服从正态分布。

实现K-S检验时，设想可以在一定的代数下（更新换代了p1次）使得各维的边缘分布在下一代中同属于上一代的各个分布，只是根据参数的不同来决定各维变量的不同分布情况。以下两种方式实现K-S检验的应用:

1）p1为固定次数，即每更新换代p1次，就应用K-S检验重新验证各维的边缘分布函数，这种静态调整可以减少估计的复杂度。

2）p1为不固定次数，因为前期阶段各维分布情况很不稳定，可以使p1值取小一些，即K-S检验验证频率相对较大一些。后期阶段各维分布情况趋于稳定，则验证频率可以相应减少，这种动态调整具有检验的灵活性。

2.2 copula EDA简单介绍

由于正态分布函数的普遍性，而且某种程度上，由中心极限定理又保证了用它可以来逼近其他分布，因此现阶段正态分布函数［3，9］应用于各种智能算法中，同时也包括copula EDA.将正态分布应用于高维copula EDA边缘分布函数的选取中，这种连续性的分布函数要比离散性分布序列采样简单的多，利用该分布函数的反函数就可以直接求得。早期的 copula EDA［10］采用二元 copula 理论［11-13］，在此基础上边缘分布采用了高斯分布验证了算法的可行性。此后将copula函数应用到MIMIC（Mutual information maximization for input clustering）算法［12］中来代替条件正态分布等。文献［14］中选用不同的copula函数（Guassian copula与Frank copula），边缘分布函数选取的Beta分布研究了算法的应用。之后，copula EDA选用clayton copula函数作为参照，对于边缘经验分布函数进行研究，使用经验分布函数［14-15］来估计变量之间的关系。

2.3 基于静态K-S检验的copula EDA

在copula EDA基础上，添加K-S检验作为确定边缘分布函数的前期工作，设想可以使得进行K-S检验的代数服从某一函数［f（x）=kxq，k=1，2…，q=1，2…］，来确定K-S检验的次数，其中，x为算法运行的代数，f（x）为进行K-S检验的代数。静态K-S检验即是静态调整K-S检验的频率，最简单的用法就是每代都进行K-S检验，也就是说令k=1，q=1.

基本算法描述如下:

步骤1:初始化群体。随机产生P个点，组成初始群体，此时进化代数g为1.

步骤2:计算适应值。根据选取的测试函数计算群体中的适应值。

步骤3:选择优势群体。本文采用截断选择和轮赌选择两种方式各选出一部分适应值较好的共s个个体作为新的种群的一部分。

步骤4:Copula函数参数选择。选用clayton copula函数为连接函数，通过PMLE估计法得到其参数thita进行仿真实验。

步骤5:估计优势群体的概率分布模型。在此运用K-S检验来验证优势群体各维服从哪一类概率分布模型，即以优势群体各维为样本，对具体的概率分布F进行验证，主要是对是否服从所假设的分布函数进行K-S检验。应用K-S检验时，根据优势群体得出相应的样本均值和样本方差，和假设的分布函数比较得出一个数值p（0＜p＜1），选定显著性水平a为0.05，如果p值小于0.05，则该样本不服从假设的分布，反之则认为样本服从假设的分布。

步骤6:根据估计的概率模型进行采样［16］，产生一些新个体。如果判断某维个体不服从假设的分布，就构造其经验分布函数，从而进行经验采样，否则进行所服从分布的相应采样。在搜索空间内按概率分布F随机产生1个点，作为新生代中的部分个体。

步骤7:更新群体。新一代群体由第g代群体中选出s个适应值较好的个体，通过采样产生的1个个体，以及通过变异所产生的PS-s-1个个体共同组成，并将进化代数g←g+1.

步骤8:若满足某种停止准则，则算法结束；否则算法转到Step2继续执行。

3 算法性能测试与分析

3.1 测试函数

为测试算法的性能，并将第3节中的算法与copula EDA进行比较，选用六个测试函数进行测试。

3.2 参数设置

种群规模取2000，维数取10，选择率为0.5，变异率为0.05.用截断选择和轮赌选择选一部分优势

个体，采用变异算子，选择出当前种群中r个优秀个体，参入变异，并将变异后的个体加入到下一代种群中。每个函数都独立运行50次。采样时，对于clayton copula参数的选取采用的策略是利用PMLE法［17-18］估计 clayton copula的参数 thita值。PMLE法估计参数可以增加种群多样性，防止过早的陷入局部最优。

表1 copula EDA与静态K-S检验的copula EDA在PMLE估计参数下的比较Tab.1 The comparison of PMLE estimation parameters of copula EDA and copula EDA of static K-S test

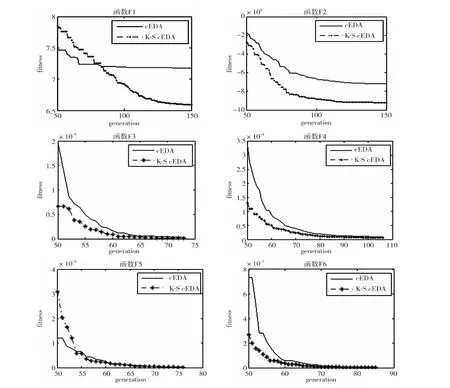
图1 六个测试函数采用两种算法一次运行的适应值Fig.1 One running time fitness of six test functions by using two kinds of algorithms

3.3 结果分析

表1的实验结果可以看到，对于六个测试函数，基于静态K-S检验的copula EDA比copula EDA的优化结果要好，说明多种分布函数同时应用到copula分布估计算法中的可行性与有效性。

图1的各图分别表示六个测试函数在一次运行过程的进化图，由于从第1代到第150代的进化图数据跨度较大，使得后期图形趋势不明显，所以进化图截取的是后几十代的图形走向。这些图直观地说明了采用基于静态K-S检验的copula EDA和copula EDA的搜索过程，从图中可以明显地观察到采用基于静态K-S检验的copula EDA比copula EDA能更快地搜索到最优值附近。

4 结论

在K-S检验的copula EDA中，重要的两个步骤是对所选择优势群体的各维变量通过K-S验证其所服从的分布，以及根据所服从的相应分布分别进行采样。基于静态K-S检验的copula EDA是各维的变量每一代都进行K-S检验。实验表明，基于静态K-S检验的copula EDA能够收敛到全局最优解，但算法的某些性能还相对较弱，在进化后期收敛的速度还不是很理想，并且算法的参数设置对于基于静态K-S检验的copula EDA的化效果影响较大。因此，以下问题值得进一步研究。

1）参数的选择问题。选取的参数不同，对算法的影响不同。

2）针对性的改进算法性能，使其具有良好的优化效果。

3）采用K-S思想动态的检验copula EDA，即基于动态K-S检验的copula EDA.

［1］周树德，孙增圻.分布估计算法综述［J］.自动化学报，2007，33（2）:113-124.

［2］LARRANAGA P，ETXEBERRIA R，LOZANO J A，et al.Optimization in Continuous Domains by Learning and Simulation of Gaussian Networks［C］∥Proceedings of the GECCO-2000 Workshop in Optimization by Building and Using Probabilistic Models.San Francisco，2000:201-204.

［3］王丽芳.Copula的分布估计算法［M］.机械工业出版社，2012.

［4］王丽芳，曾建潮，洪毅.利用 Copula函数估计概率模型并采样的分布估计算法［J］.控制与决策，2011，26（9）:1333-1338.

［5］杨兴民.Copula理论及其在相关分析中的应用［D］.济南:山东大学，2007.

［6］侯澍旻，李友荣，刘光临.K-S检验在轴承故障诊断中的应用［J］.煤矿机械，2004（1）:129-130.

［7］吴喜之.非参数统计［M］.北京:中国统计出版社，1992.

［8］STEPHENS M A.“Tests based on EDF Statistics.”In Goodness-of-Fit Techniques［M］.Macel Dekker，New York，1986:97-195.

［9］杨茹.Clayton Copula分布估计算法中边缘分布的研究［D］.太原:太原科技大学，2011.

［10］WANG L，ZENG J，HONG Y.Estimation of Distribution Algorithm Based on Copula Theory［C］∥IEEE Congress on Evolutionary Computation 2009.Trondheim，Norway，2009:1057-1063.

［11］WANG L，ZENG J.Estimation of Distribution Based on Copula Theory［M］∥Exploitation of Linkage Learning in Evolutionary Algorithms.NY:Springer，2010:139-162.

［12］WANG L，ZENG J，HONG Y.Estimation of Distribution Based on Archimedean Copulas［C］∥2009 World Summit on Genetic and Evolutionary Computation.Shanghai，China，2009:993-996.

［13］SALINAS-GUTIERREZ R，HERNANDEZ-AGUIRRE A，VILLA-DIHARCE E R.Using Copulas in Estimation of Distribution Algorithms［M］∥LNAI 5845，MICAI 2009.NY:Spring，2009:658-668.

［14］WANG L，WANG Y，ZENG J，et al.An Estimation of Distribution Algorithm Based on Clayton Copula and Empirical Margin［C］∥ Life System Modeling and Intelligent Computing，Communications in Computer and Information Science.Wuxi，China，2010，98（1）:82-88.

［15］WANG L，ZENG J，HONG Y.Using Gumbel Copula and Empirical Marginal Distribution in Estimation of Distribution Algorithm［C］∥2010 Third International Workshop on Advanced Computational Intelligence（IWACI 2010）.Suzhou，China，2010:583-587.

［16］WANG L，ZENG J，HONG Y，et al.Copula Estimation of Distribution Algorithm Sampling from Clayton Copula［J］.Journal of Computational Information Systems，2010，6（7）:2431-2440

［17］GUO X，WANG L，ZENG J，et al.Copula Estimation of Distribution Algorithm with PMLE［C］∥20117th International Conference on Natural Computation.Shanhai，China，2011:1077-1081.

［18］邱小霞，刘次华，吴娟.Copula函数中参数极大似然估计的性质［J］.经济学，2008，25（2）:212-215.