修正的Arrhenius方程与过渡状态理论*

刘国杰 黑恩成

(华东理工大学化学系 上海 200237)

前文[1]已通过对Arrhenius活化能理论的分析，建立了一个修正的Arrhenius方程：

k=BTne-E/RT

(1)

式中B，n，E是方程的3个参数。式(1)已被证明能够满意地描述宽阔温度范围内反应速率常数随温度的变化规律。几乎在所有的物理化学教科书中，都提到了这个方程。但是，毫无例外地都将它视为经验方程，认为3个参数只是实验数据的拟合值，没有任何物理意义。本文提出了不同的看法。其实，式(1)在某种情况下是可由过渡状态理论导出的，此时它与熟知的Eyring方程是等价的，且3个参数都有明确的物理意义。

1 过渡状态理论的基本假设

过渡状态理论建筑在量子力学对势能面计算的基础之上，它指出了化学反应最可能进行的途径，亦称反应坐标。按照这条途径，Eyring等[2]提出了如下3点基本假设：

① 基元反应是以下列反应模式进行的：

② 在反应过程中，反应物与活化络合物始终处在热力学平衡状态，这就是说它们的能量都遵守Boltzmann分布。

③ 反应速率取决于活化络合物分子越过能垒，分解成产物分子的速率。且活化络合物分子一经越过能垒而变成产物分子后，便一去不复返。

于是，由假设②可得:

(2)

由假设③可得反应速率：

(3)

式中ν为活化络合物分子的分解频率，亦即活化络合物分子平均寿命的倒数。因此，反应速率常数当为：

(4)

式中的分解频率ν等于活化络合物分子沿着反应坐标的不对称伸缩振动的频率。这个振子的特殊结构决定了它的振动频率很低，kBT≫hν，其配分函数为：

(5)

(6)

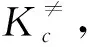
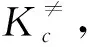
2 分解频率ν与参数n的物理意义

量子力学指出，当能量标度的零点设在基态能级上时，振子的能量为：

εov=υhν

(7)

式中υ为振动量子数，其值可取0，1，2，…，每个值相当于振子的一个能级。由于活化络合物分子沿着反应坐标的不对称伸缩振动的频率很低，振子的能级间隔很小，以致反应系统中的活化络合物分子散布在可及的能级中，其平均能量应为：

(8)

鉴于活化络合物分子的能量服从Boltzmann分布，它的平均能量也可由统计力学方法计算：

(9)

式中的qov由式(5)代入。因此，由式(8)和式(9)可得：

(10)

(11)

式中α是个正数。将式(11)代入式(10)，便得：

hν=kBT(1-α)=kBTn

(12)

式中n=1-α，当α>1时，n是负数。

由式(12)可见，n的大小与振子能级的间隔hν密切相关。当指定反应温度时，n越大，hν越大；反之，n越小，hν越小；也就是说，n是一个衡量活化络合物分子分解频率大小的参数，这就是式(1)中参数n的物理意义。

3 平衡常数与参数B和E的物理意义

(13)

(14)

只要将式(12)和式(14)代入式(4)，便得反应速率常数:

(15)

已知反应活化能的定义式[3]为:

(16)

式中ν即上述过渡状态理论反应模式中第二步的反应速率常数k2。式(16)中还代入了式(4)和Van′t Hoff方程。现将式(16)代入式(15)，可得：

(17)

对于溶液反应，Δ≠(pVm)≈0，e-Δ≠(pVm)/RT≈1，则有：

(18)

k=BTne-E/RT

这就是修正的Arrhenius方程。

对于气相反应，若压力不高，Δ≠(pVm)=-RT，e-Δ≠(pVm)/RT=e，则有：

(19)

k=BTne-E/RT

此式亦即修正的Arrhenius方程。

倘若气相反应为单分子反应，Δ≠(pVm)=0，则所得结果与式(18)相同。总之，由过渡状态理论不难导出修正的Arrhenius方程。

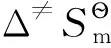
4 修正的Arrhenius方程与Eyring方程的关系

应该指出，本文与Eyring方程中有关标准摩尔活化热力学函数的定义是不同的，本文的定义式如式(13)所示，为：

(20)

而Eyring方程中的定义式为：

(21)

(22)

鉴于本文已导得沿反应坐标的振子配分函数如式(5)表示，它与式(10)比较可得qov=υ。若再代入式(11)，便得与K≠的关系为:

(23)

将式(23)代入Eyring方程(式(6))，则得:

(24)

式中代入了式(20)，其中n=1-α。式(24)即为式(15)。据此，不难得到修正的Arrhenius方程。

由此可见，利用本文建立的式(23)，可由Eyring方程导出修正的Arrhenius方程。反之，由修正的Arrhenius方程亦不难导出Eyring方程，这表明两者是等价的。不过，应该指出，据此得出的修正的Arrhenius方程只适用于n为负数的情况。而实际上，参数n的值可正也可负，这个欠缺是由于Eyring方程只适用于kBT≫hν，而不适用于hν≥kBT所致。

5 结论

综上所述，可以得出如下两点结论：

① 修正的Arrhenius方程(即式(1))，可由过渡状态理论的基本假设出发从理论上导出，而且它与Eyring方程等价，是过渡状态理论的另一种表示形式。但是，它只适用于参数n为负数的情况，因此，还有待进一步深入研究。

② 修正的Arrhenius方程的3个参数(B，E和n)并非经验参数，它们都有明确的物理意义。其中B是个结构参数，它与反应物转变成活化络合物的标准摩尔熵变或结构变化的无序程度有关；参数E是反应的活化能，即反应物活化成活化络合物所需的标准摩尔热力学能；n是一个频率参数，它是活化络合物分子分解频率大小的量度。

参 考 文 献

[1] 刘国杰,黑恩成.大学化学,2013,28(2):77

[2] 唐有祺.统计力学及其在物理化学中的应用.北京:科学出版社,1979

[3] 刘国杰,黑恩成.大学化学，28(5):73

[4] 刘国杰,黑恩成.大学化学,28(5):69