汽轮机螺栓松弛对汽缸蠕变强度的影响

毛剑峰， 王炜哲，2， 张军辉， 陈汉平

（1．上海交通大学 机械与动力工程学院，动力机械与工程教育部重点实验室，上海200240；2．上海交通大学 机械与动力工程学院，机械系统与振动国家重点实验室，上海200240；3．上海电气电站设备有限公司汽轮机厂，上海200240）

汽轮机上下汽缸往往通过高温法兰和螺栓进行连接，并在初始装配中，施加螺栓一定预紧力产生弹性变形，以保证汽缸的紧密性．然而，随着蒸汽温度参数的提高，螺栓及汽缸的高温蠕变特性会导致螺栓应力松弛，从而严重影响汽缸的紧密性．因此，研究螺栓在长期高温环境中的应力松弛特性，对汽缸的紧密性具有重要意义．

国内外学者针对螺栓高温特性开展了大量研究．常温下，螺栓预紧力可根据密封性要求进行计算，而高温下，由于螺栓松弛导致预紧力下降，从而降低法兰连接结构的密封性能，因此需要考虑高温下螺栓松弛对汽缸结构强度的影响［1］．为此许多研究者采用了不同的分析手段，开展了螺栓及相关高温部件蠕变强度的研究．张晓昱等［2］采用加速蠕变断裂试验法对运行3．5×105h的12%Cr钢高温螺栓材料进行了寿命评估，结果表明螺栓的过度松弛导致断裂时间远小于设计值．杜运新等［3］采用数值模拟方法获取了构件变形对承压型高强螺栓应力分布的影响，模拟降温过程中高强度螺栓预紧力特性，并进一步阐述了摩擦力和法向接触力对构件强度的影响．在实际汽轮机运行中，陈以超［4］对引进型300MW汽轮机高温螺栓断裂问题进行了探讨，针对螺栓伸长量进行了计算及评估．刘彤等［5］针对锅炉炉内包括螺栓在内的承压部件进行寿命损耗规律的分析，采用拉森－米勒参数法确定蠕变断裂时间，用罗宾逊法求出过热器蠕变寿命损耗．蔡连元等［6］应用等温线法和拉森－米勒参数法对应用在主蒸汽管道上的法兰接头P91钢材料进行持久强度外推，进而估算了其蠕变寿命．郭进全等［7］进一步研究了国产1Cr10NiMoW2VNbN螺栓材料的长时应力松弛性能，对该材料进行了松弛试验，认为多项式数学模型可以较好地外推松弛剩余应力．综上所述，以往的研究主要针对螺栓部件进行高温强度及松弛特性分析，并没有考虑螺栓与汽缸本体之间耦合作用下螺栓的高温蠕变及松弛特性．此外，工程设计中的保守设计思路是采用高温螺栓剩余应力（图1中σ3）作为保证汽缸中分面密封的最小应力（不考虑螺栓松弛效应）．实际上，汽缸中分面的剩余密封应力是装配预紧力、汽缸蠕变和螺栓蠕变共同作用的结果．因此，考虑螺栓松弛效应作用下，耦合计算汽缸和螺栓的应力应变具有重要的工程价值．

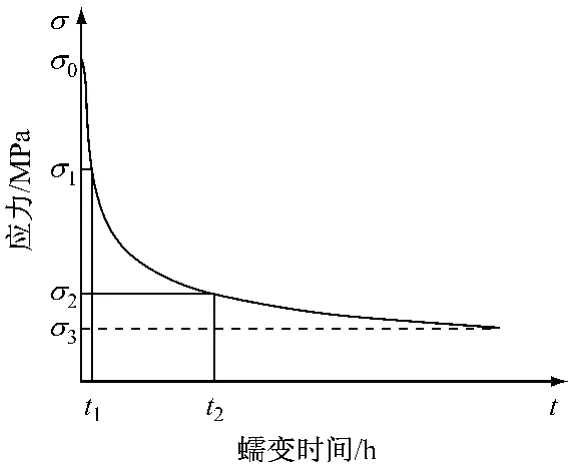
图1 应力松弛曲线Fig．1 The stress relaxation curve

笔者针对某1000MW汽轮机中螺栓连接的中压内缸结构进行2×105h蠕变数值计算，分析和比较了考虑和未考虑螺栓松弛两种情况下的最大主应变、Mises应力的变化规律，进而采用Larson－Miller方法来预测不同时刻应力条件下的断裂时间，并结合连续性蠕变损伤力学模型计算不同时刻的蠕变损伤．

1 计算模型

1．1 本构模型

针对汽缸和螺栓的蠕变过程，采用时间硬化的Norton－Bailey蠕变本构模型进行计算和分析，公式如下［8］：

式中：εc、t和σ分别为材料的蠕变应变、时间和应力；A、p和q为材料参数，通过材料试验数据的拟合获取（材料试验数据来自于某厂家）．

为了说明长期运行在高温环境下螺栓和汽缸的蠕变损伤特征，采用连续性损伤力学模型进行高温强度的评估，其表达式为［9－10］

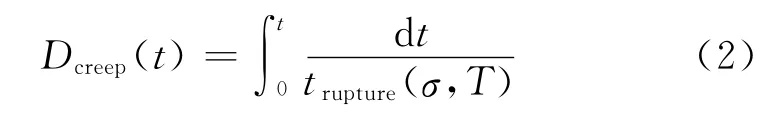
式中：trupture（σ，T）是在应力σ和温度T 工况下的蠕变断裂时间．

蠕变损伤取决于载荷应力σ、工作温度T和承载时间．为了求解不同载荷和时间条件下的蠕变断裂时间，采用基于载荷应力σ的Larson－Miller参数法来进行分析，进而获得断裂时间．其中，基于断裂时间的Larson－Miller参数法计算公式为［11］ΨLMP＝T［C＋log（trupture）］ （3）式中：C为常数，当温度为473℃时，取C＝20．38，当温度为586℃时，取C＝17．30．

基于载荷应力σ的Larson－Miller参数法计算公式为［11］Ψ（σ）＝α＋β·σλ（4）式中：α、β和λ为根据材料试验数据拟合得到的参数．利用图2所示汽缸材料的试验数据［12］，拟合得到α＝0，β＝39．2，λ＝－0．113 2，并对比式（3）和式（4），在给定温度T和载荷应力σ的条件下，可以得到对应的蠕变断裂时间trupture．

1．2 有限元模型

以某1000MW汽轮机中压内缸和中分面螺栓组件为计算对象，由于左右对称，取其一半作为计算域，其中包括汽缸、中分面法兰及连接螺栓的完整结构（如图3（c）所示）．汽缸中部为进汽段，蒸汽参数为628℃和11．5MPa．为了考察蠕变松弛的发展过程，进行了2×105h蠕变计算．

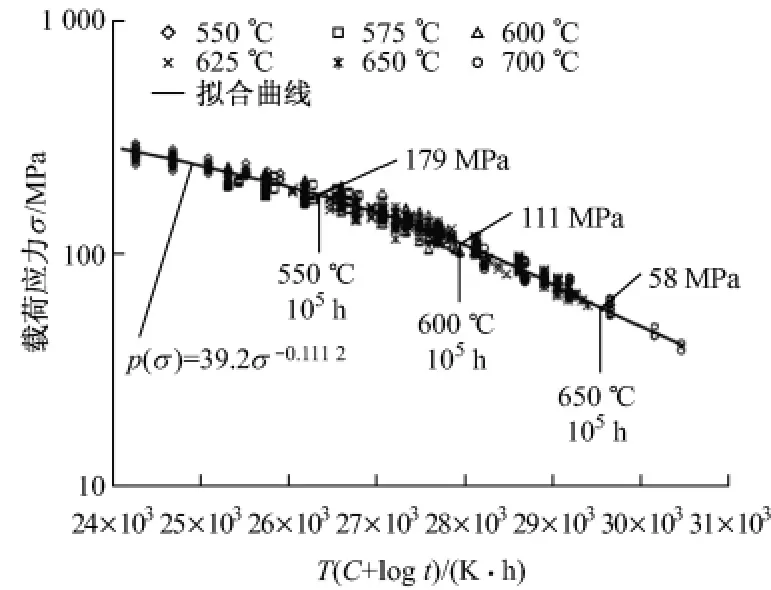
图2 汽缸材料的Larson－Miller参数评估图［13］Fig．2 Larson－Miller diagram for evaluating creep－rupture strength of casing material

计算中，汽缸和螺栓分别采用四节点四面体非结构化和八节点六面体结构化网格热力耦合单元（见图3（a）和图3（b）），单元总数为145 920．为了比较考虑和未考虑螺栓松弛对汽缸强度的影响，选取图3（a）、图3（b）上标注的1、2和3三个特征位置进行分析，其中位置1和位置2靠近螺栓孔，位置3接近高温进口蒸汽．

约束边界如图3（c）所示：汽缸对称面施加y向对称约束；左侧支撑部位施加x向位移约束；并在两个支撑部位的汽缸中分面上施加z向约束．蒸汽与本体设备的传热系数由生产厂家提供．螺栓与法兰之间采用接触面设置，并在螺栓上增加装配预紧力的约束方法．

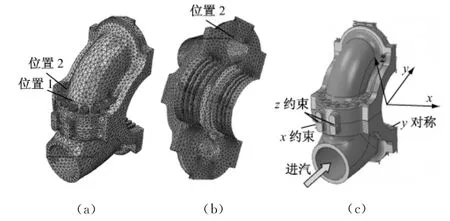
图3 汽缸中间部分的三维几何模型及网格分布Fig．3 3Dgeometric model and grid division of the turbine casing

为了考察螺栓松弛对汽缸应力、应变和损伤的影响，采用Abaqus进行耦合计算，并且分别在考虑和未考虑（最小剩余应力作为汽缸中分面恒定预紧力）螺栓松弛条件下，对汽缸进行了2×105h蠕变计算．

2 结果与分析

图4 汽缸中分面螺栓孔附近的温度场Fig．4 Temperature distribution on casing split near bolt holes

图4给出了汽缸中分面螺栓孔附近温度场分布图．由图4可以看出，螺栓所处位置温度已超过450℃，蠕变效应对螺栓的影响较明显，因此需要考虑螺栓松弛对汽缸应力、应变和损伤的影响．

图5给出了位置1、位置2和位置3在考虑和未考虑螺栓松弛效应下的最大主应变随时间的变化情况．从图5可以看出，随着蠕变时间的增加，不论是否考虑螺栓松弛，主应变的增加都趋于平缓，说明蠕变进入了稳定松弛阶段，但蠕变历程绝对值差异明显．此外，位置1和位置2处考虑螺栓松弛效应时，汽缸最大主应变绝对值增大，这是因为螺栓在松弛过程中，作用于汽缸上的应力始终大于最小剩余应力（如图1），从而使得汽缸上承载较大的载荷．然而，位置3处考虑和未考虑螺栓松弛效应时主应变差异较小，这是由于位置3距离螺栓孔较远，螺栓载荷对其影响较小．此外，对比图5计算结果可以看出，位置1和位置2的最大主应变均小于位置3的最大主应变，其原因在于位置3处温度较高，蠕变变形较大．

为了评估考虑和未考虑螺栓松弛情况下汽缸的损伤，先对2种情况下应力和蠕变时间历程进行分析，并应用Larson－Miller公式获取蠕变断裂时间，从而求解蠕变损伤．图6给出了位置1、位置2和位置3在2类计算边界条件下的Mises应力随时间的变化情况．从图6可以看出，随着蠕变时间增加，考虑螺栓松弛时，位置1和位置2处的Mises应力下降较快，且两者之间的差异也越来越明显．然而，2种情况下位置3处的Mises应力差别较小．由此可以说明，越靠近螺栓位置的汽缸部位，螺栓松弛效应对其应力的影响越明显．为了最终得到蠕变损伤的变化趋势，需要先定量地拟合图6中的应力－时间曲线以得到相应的数学关系式．为此得到未考虑螺栓松弛效应下，能较好反映应力随时间变化规律的关系式：σ（t）＝329．6t－0．0487（位 置 1）、σ（t）＝355t－0．0582（位置2）和σ（t）＝1 245．76t－0．3402（位置3）；考虑螺栓松弛影响下，能较好反映应力随时间变化规律的关系式：σ（t）＝386＋204．9t－0．5＋32．7t0．2（位置1）、σ（t）＝366．7＋235．8t－0．5－28．6t0．2（位置2）和σ（t）＝1 210．7t－0．336（位置3）．从图6可进一步看出，多项式指数拟合式更能贴近有螺栓松弛效应情况下汽缸中靠近螺栓位置的应力变化趋势；而单项式指数拟合式则更贴近无螺栓松弛效应情况下汽缸的应力变化趋势．因此，汽缸应力松弛不单是自身作用，还受螺栓松弛和初始预紧力多重因素的影响，即所谓的多重机制的影响．相反，由于在无螺栓松弛效应情况下螺栓作用力始终一定，所以汽缸应力松弛只是自身在起作用，即所谓的单机制影响．将得到的应力－时间拟合式带入式（4）中，求解出不同时刻的Ψ（σ），进而将此值带入式（3）中求解出对应时间应力下的蠕变断裂时间，从而求解出此时刻损伤，最终外推到4×105h累积蠕变损伤，其结果见图7．

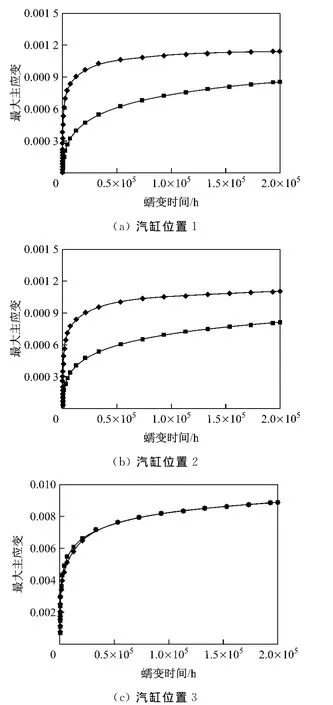
图5 考虑和未考虑螺栓松弛情况下汽缸不同位置的应变曲线Fig．5 Strain curves of turbine casing at different locations with and without consideration of bolt relaxation

图6 考虑和未考虑螺栓松弛情况下汽缸不同位置的应力松弛Fig．6 Mises stress curves of turbine casing at different locations with and without consideration of bolt relaxation

由图7可以看出，位置3的蠕变损伤变化可以明显地分为2个阶段，分别为前期的过渡松弛阶段（8×104h之前）和后期的稳定松弛阶段（8×104h之后）．以位置3呈现的2个阶段为参照，从图7可进一步看出，位置1、位置2在过渡松弛阶段的蠕变损伤增加较慢，而在稳定松弛阶段的蠕变损伤增加较快．同时还可以看出，螺栓松弛效应加速了汽缸蠕变损伤的发展．但是，远离螺栓孔的位置3的汽缸蠕变损伤受螺栓松弛的影响相当有限．由此可见，在距离螺栓较近的位置处，螺栓松弛将对汽缸的损伤产生重大影响．此外，图7中所示考虑螺栓松弛影响时，位置1的2×105h蠕变损伤达到0．24，而不考虑螺栓松弛影响时，位置1的2×105h蠕变损伤仅为0．12．

图7 汽缸不同位置在螺栓松弛与无螺栓松弛效应影响下的蠕变累积损伤度Fig．7 Creep－damage curves of turbine casing at different locations with and without consideration of bolt relaxation

3 结 论

（1）螺栓松弛对汽缸蠕变损伤有补偿作用，不考虑螺栓松弛效应下，汽缸应力和蠕变损伤计算具有保守性．

（2）螺栓松弛效应与几何位置密切相关．靠近螺栓孔的位置受到强烈的螺栓松弛补偿，汽缸应力松弛曲线受多重机制的影响，拟合曲线呈多项复杂指数函数形式，而远离螺栓孔处螺栓松弛的补偿效果有限．

（3）螺栓松弛效应加速了汽缸蠕变损伤的发展．但是螺栓松弛效应对远离螺栓孔位置的蠕变损伤影响相当有限．从定量分析，考虑螺栓松弛影响时，位置1的2×105h蠕变损伤为0．24，而不考虑螺栓松弛影响时，位置1的2×105h蠕变损伤仅为0．12．

［1］丁有宇．汽轮机强度计算手册［M］．北京：中国电力出版社，2010．

［2］张晓昱，欧阳杰，吴楠，等．基于加速蠕变断裂试验的12%Cr钢高温螺栓安全可靠性评价研究［J］．汽轮机技术，2009，51（4）：318－320．ZHANG Xiaoyu，OUYANG Jie，WU Nan，et al．The research on safe reliability evaluation of 12%Cr－steel high－temprature bolt based on accelerated creep rupture test［J］．Turbine Technology，2009，51（4）：318－320．

［3］杜运新，宦慧玲，霍静思．构件强度控制的高强螺栓承压型连接研究［J］．湖南大学学报：自然科学版，2011，38（1）：8－12．DU Yunxin，HUAN Huiling，HUO Jingsi．Study of high strength bolted bearing－type joint controlled by member strength［J］．Journal of Hunan University：Natural Sciences，2011，38（1）：8－12．

［4］陈以超．引进型300MW汽轮机高温螺栓断裂问题探讨［J］．华中电力，2002，15（3）：61－63．CHEN Yichao．Study on the cracking problem about the high temp bolts for imported type 300MW steam turbine［J］．Central China Electric Power，2002，15（3）：61－63．

［5］刘彤，徐钢，庞力平，等．锅炉炉内承压部件的蠕变分析及寿命计算［J］．动力工程，2004，24（5）：631－635．LIU Tong，XU Gang，PANG Liping，et al．Creep analysis and life calculation of the pressure components inside boiler［J］．Journal of Power Engineering，2004，24（5）：631－635．

［6］蔡连元，李益民，史志刚，等．P91主蒸汽管道焊接接头的蠕变特性和寿命估算［J］．动力工程，2007，27（3）：469－472．CAI Lianyuan，LI Yimin，SHI Zhigang，et al．Creep properties and creep life estimation of welds in P91 steel fresh steam pipes［J］．Journal of Power Engineering，2007，27（3）：469－472．

［7］郭进全，轩福贞，何磊．螺栓材料1Cr10NiMoW2VNbN的应力松弛行为及预测模型［J］．核动力工程，2008，29（6）：119－124．GUO Jinquan，XUAN Fuzhen，HE Lei．Stress relaxation performance and prediction models for bolt material of 1Cr10NiMoW2VNbN［J］．Nuclear Power Engineering，2008，29（6）：119－124．

［8］NORTON F H．The creep of steel at high temperatures［M］．New York：McGraw－Hill，1929．

［9］LAM Tony C－T，TRAN Suong，DEWEY Robert P．Predicting creep initiation in gas turbine blades［C］／／Proceedings of PWR2005．Chicago，USA：ASME，2005．

［10］VISWANATHAN R．Damage mechanisms and life assessment of high－temperature components［M］．USA ：ASME Int．Gas Turbine，1989．

［11］DAVIS J R．ASTM E139Standard test method for conducting creep，creep－rupture，and stress－rupture tests of metallic materials［S］．USA：ASME，2000．

［12］BENDICK W，GRABREL J，VANDENBERGHE B．Assessment of creep rupture strength for new martensitic 9%Cr steels［C］／／Eighth International Conference on Creep and Fatigue at Elevated Temperatures．San Antonio，Texax，USA：ASME，2007．