蒸汽发生器水位控制器的多目标GA和静态H∞回路成形优化设计

周世梁， 刘玉燕， 段 锋

（1．华北电力大学 核科学与工程学院，北京102206；2．华北电力大学 控制与计算机工程学院，北京102206；3．中广核工程有限公司，深圳518124）

在核电厂运行过程中，当蒸汽发生器水位低于给水环时，蒸汽有可能进入给水环，可导致“水锤”现象，从而损坏给水环；若水位继续下降到低于U形传热管束顶部时，会导致传热恶化；若水位进一步下降，会导致蒸汽发生器管板承受过大热冲击．而水位过高时，会影响汽水分离效果，造成蒸汽品质恶化，危害汽轮机的叶片．因此，蒸汽发生器水位控制系统的性能是影响核电站机组安全经济运行的重要因素之一．

蒸汽发生器是一个高度复杂的非线性、时变的非最小相位系统，并且蒸汽发生器存在“收缩”与“膨胀”的逆动力学效应以及随运行功率而变化的动力学特性［1］，因而蒸汽发生器的水位控制很复杂．

尽管学者们提出了许多先进的蒸汽发生器水位控制方法［2－3］，但对于核电厂过程控制这类可靠性要求很高且倾向于采用传统成熟技术的系统来说，在不改变控制策略和控制器类型的情况下［4］，优化控制器参数是更容易被核电运营方和核安全当局接受的方案．目前，绝大部分核电厂蒸汽发生器水位控制系统在高负荷下采用前馈－反馈串级三冲量控制，并采用PID作为主、副调节器；在低负荷下采用蒸汽流量前馈和水位反馈控制，并采用PID作为水位控制器．

笔者采用静态H∞回路成形设计方法（Loop Shaping Design Procedure，LSDP）［5］设计了低负荷下蒸汽发生器水位的鲁棒比例微分串联滤波器型控制器．该方法通过求解一组线性矩阵不等式，可得出给定结构权函数W1下静态输出反馈H∞控制器K∞，最终所得控制器W1K∞能保证控制系统的鲁棒稳定性和鲁棒性能，且具有与权函数W1相同的结构．对于蒸汽发生器水位对象，选择合适参数的PD串联滤波器结构的权函数，就能得到满足期望性能要求的PID控制器参数．

1 静态H∞回路成形控制器的设计

对于不确定的成形对象，鲁棒控制器的综合使用标准化互质因子形式或者等效的4块H∞框架［6］如图1所示．其中，ω1和ω2为外界干扰；z1和z2为评价输出；G为被控对象；W1和W2为权函数；K∞为H∞控制器；Gs为成形后对象．

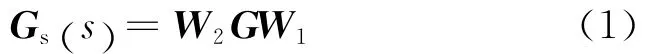
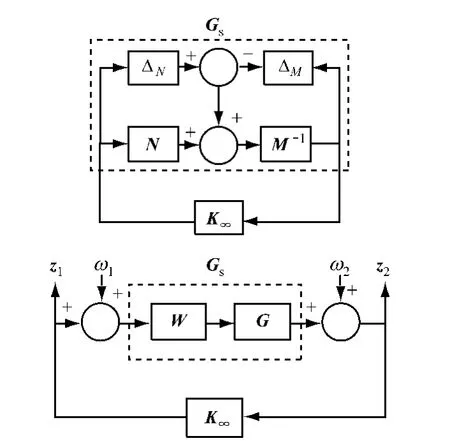
图1 H∞回路成形控制器4块合成框图Fig．1 Block diagram of H∞loop shaping control

权函数W1和W2的选取原则为：在低频段，使Gs的奇异值大于某设计期望值，以保证系统取得期望的输入跟踪能力和抗干扰能力；在高频段，使Gs的奇异值小于某设计期望值，以获得期望的噪声抑制效果；在过渡频率段，与调节时间相关的奇异值穿越频率应大于某设计期望值，且为了保证闭环系统的稳定性，应使Gs的奇异值曲线斜率小于－40 dB／dec；W1和W2中不包含使Gs不稳定的隐含模态．设成形后对象Gs的最小状态空间实现为且（A，B）和（A，C）分别可控和可观．为了简单起见，设D＝0．为了确保良好的鲁棒稳定性裕度，考虑成型对象的互质因子不确定性来设计Gs的稳定控制器．设Gs的标准化左互质因式分解为

其中M、N的状态空间实现如下［5］

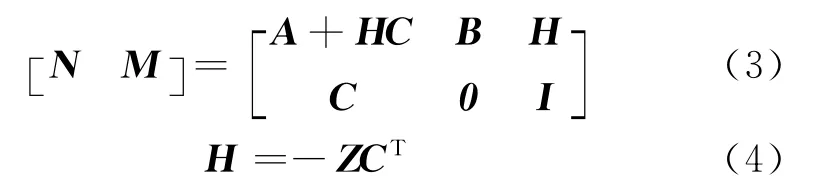
Z≥0为式（5）所示代数Riccati方程的唯一稳定解．

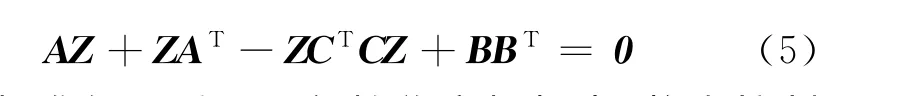
在标准化互质因子鲁棒稳定框架中，静态控制器K∞的综合必须满足

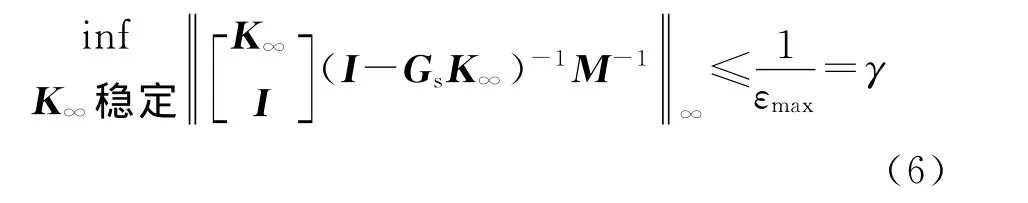
式中：εmax为可取得的最大鲁棒稳定裕量．

求解以下线性矩阵不等式（Linear Matrix Inequality，LMI），得到满足式 （7）和 式（8）的最小β值和正定矩阵P

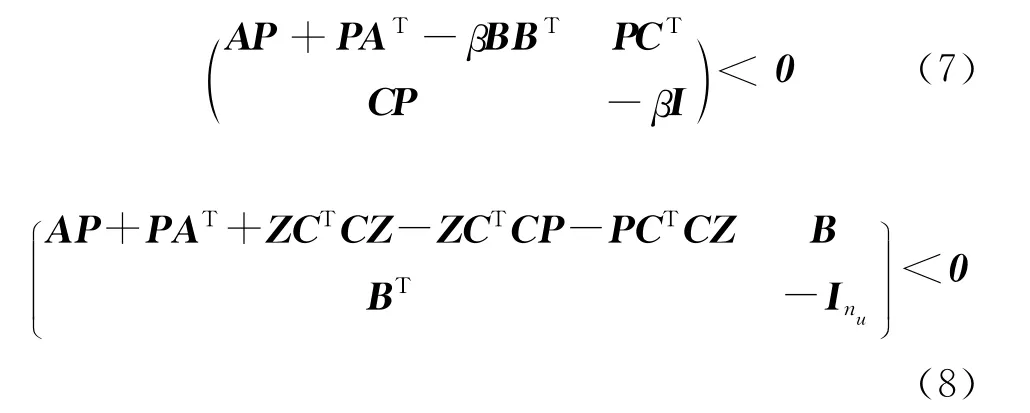
若式（7）和式（8）有解，表明存在满足式（6）的静态H∞回路成形控制器K∞，最大鲁棒稳定裕度εmax由式（9）给出

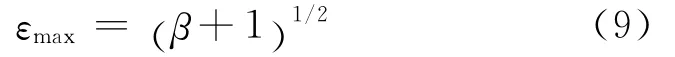
然后求解以下矩阵不等式，得到静态H∞控制器K∞．

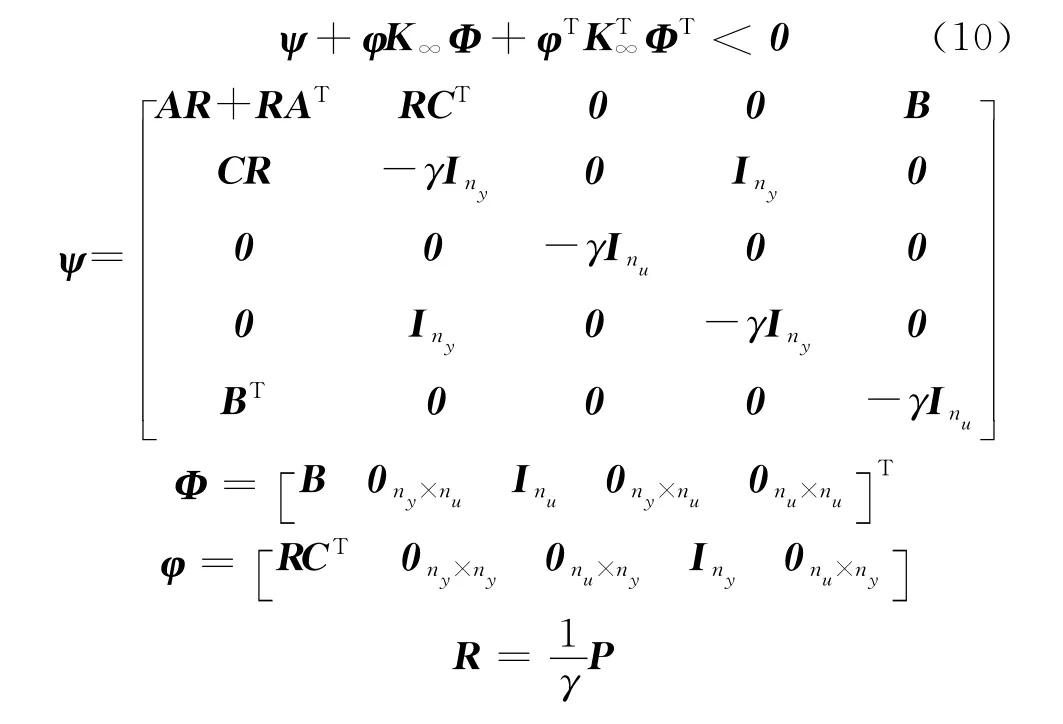
最后，结合权函数与静态控制器K∞，得到H∞回路成形控制器W1K∞．单输入单输出系统控制器的结构与权函数结构一致．

2 蒸汽发生器水位控制仿真模型

采用的仿真模型为E．Irving提出的蒸汽发生器集中参数模型［7］：

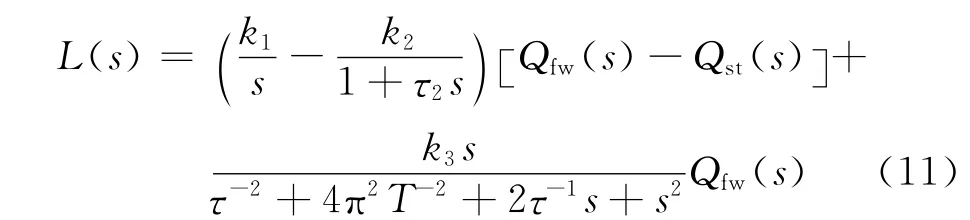
式中：s为复频率；L（s）、Qfw（s）和Qst（s）分别为蒸汽发生器的水位l（t）、给水流量qfw（t）和出口蒸汽流量qst（t）的拉普拉斯变换．

式（11）中，k1、k2、k3、τ、τ2和T 的取值随功率不同而不同．表1给出各参数在5%和15%额定功率点处的取值，其中P为实际功率，Pn为额定功率．因本文仅阐述低负荷下蒸汽发生器水位控制器的设计，为节省篇幅，表1中未给出其他功率水平下传递函数式（11）的参数．

在调节阀两侧压力波动不大的情况下，调节阀的传递函数可取为［8］

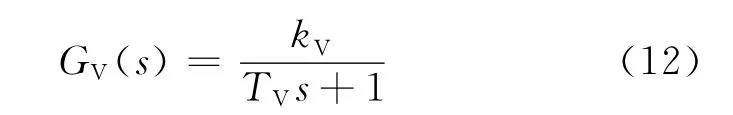
式中：0．75≤kV≤3；0．75＜TV＜3．

3 给定结构控制器的设计

3．1 控制策略

对于一般压水堆核电厂，在15%以下负荷，由于蒸汽参数低，测量流量的节流装置压差太小，使流量测量不准确，信噪比过小，因而调节回路中没有设置给水－蒸汽流量失配的前馈控制回路．为了加快控制过程响应速度，改善水位控制器的特性，引入总蒸汽流量信号作为超前控制信号，其中总蒸汽流量中的汽轮机蒸汽流量信号采用了窄量程的汽机入口压力信号，以提高其测量精度．另外，低负荷下水位的“收缩膨胀”效应更显著，因而蒸汽发生器水位自动控制系统的设计更具有挑战性．笔者仅阐述利用静态H∞回路成形方法设计低负荷（5%～15%满功率）下蒸汽发生器的水位控制器．控制系统结构如图2所示．图中，GL、GV和GFW分别表示水位控制器、阀门对象和蒸汽发生器水位对象的传递函数；lref、l、qst和qfw分别表示水位设定值、水位测量值、给水流量和蒸汽流量．

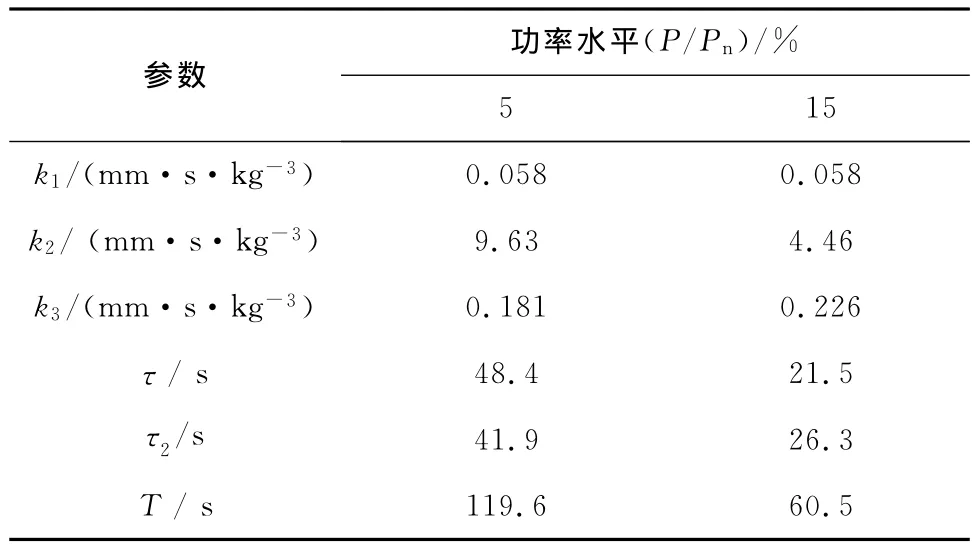
表1 蒸汽发生器水位模型参数的取值Tab．1 Parameters setting for steam generator water level model

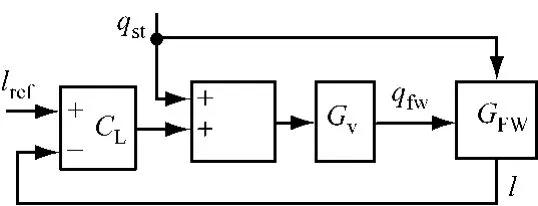
图2 低负荷下蒸汽发生器蒸汽流量前馈－水位反馈控制方框图Fig．2 Block diagram of steam flow feed forward－water level feedback control for steam generator at low load

3．2 静态H∞回路成形设计方法

广义主对象的传递函数为

式中：GFW为蒸汽发生器给水流量到水位的传递函数．

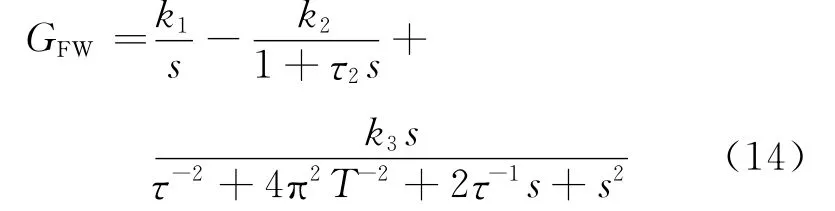
权函数W2取单位阵，权函数W1取PD串联滤波器形式，即：

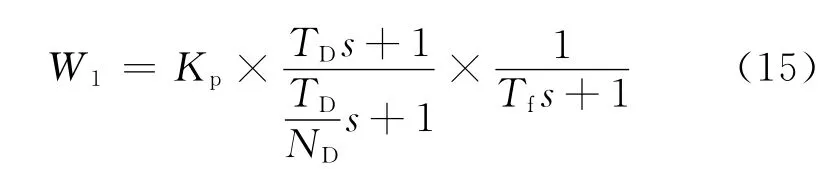
为了保证低负荷下的调节品质，选择5%工况点模型为标称模型来设计低负荷下的控制器．权函数参数的选择是否合适对控制效果影响很大．

利用H∞成形方法设计所得控制器的性能对权函数的参数很敏感，传统的权函数参数选取方法是凭设计经验反复试凑，该方法的缺点是费时费力．近年来，国内外专家学者针对权函数参数的选取进行了一些研究，但大多基于复杂的理论和推导［9］，实现困难，且所得权函数阶次较高，导致最终控制器W1K∞W2阶次更高．

H∞回路成形方法需要在鲁棒性和控制性能间取得折衷．而控制性能的不同指标（如调节时间、超调量、抗干扰能力和噪声抑制能力等）对于不同的被控对象存在一定的相互制约关系．理想的回路形状是开环对象在低频段具有较大奇异值、高频段具有较小奇异值、中频段穿越频率值较大而穿越斜率绝对值较小［6］．一般单目标优化方法很难在鲁棒稳定性和多个控制性能指标之间取得良好的平衡．针对单目标优化方法的局限性，采用多目标遗传算法（MOGA，Multi－objective GA）对能使系统奇异值形状和鲁棒裕量尽可能满足设计要求的权函数W1的参数进行全局寻优［10］．

适用度定义如下：

式中：Gs＝GW1为成形后对象；gL为低频段［0，ωL］最小可接受增益值；gH为高频段［ωH，∞］最大可接受增益值；ωCD为设计期望的穿越频率值；ωC为穿越频率，数值计算取其中i满足式（22）

3．3 其他H∞回路成形设计方法

为了验证所提方法的有效性，第4节将对本文所提方法及其他3种基于H∞成形方法的固定结构鲁棒控制器设计方法进行对比仿真试验．

3．3．1 标准H∞回路成形设计方法

作为对比的第一种方法为标准H∞回路成形方法［6］．假设被控对象（）G s的最小实现形式为

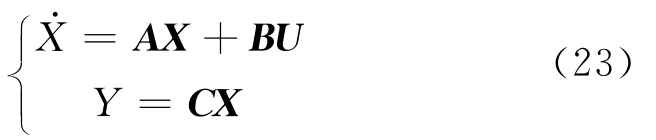
其中X和Y均为代数Riccati方程（24）的唯一半正定解．H∞最优控制器（）K s的状态空间实现为［11］

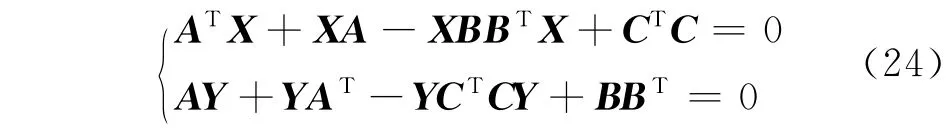
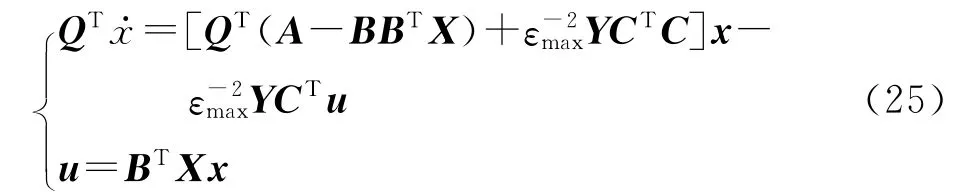
其中

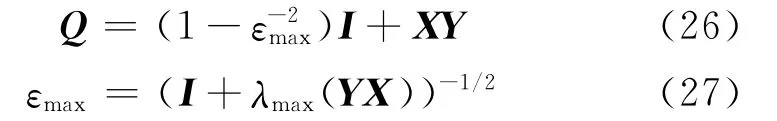
3．3．2 标准H∞回路成形降阶控制器设计方法

第二种方法也是基于标准H∞回路成形方法得出的，但采用文献［8］中所提方法将高阶控制器降阶为具有PID形式的低阶控制器．以下简称H∞回路成形降阶控制器设计（Loop Shaping Reduced Order Controller Design，H∞LSROCD）方法．

设由H∞回路成形方法得到的高阶控制器状态空间描述为：

根据控制器的频域特性，可采用以下方法获得高阶控制器的PID控制器近似．步骤如下：

（1）对AC进行相似变换，使得AC的零特征值和非零特征值分开，即

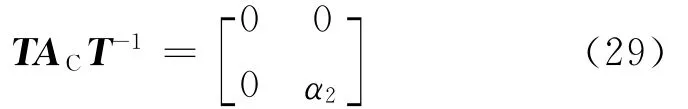
式中：α2不含零特征值．

（2）对BC和CC进行相应转换

（3）高阶控制器的PID近似为 KP＋KI／s＋KDs，其中

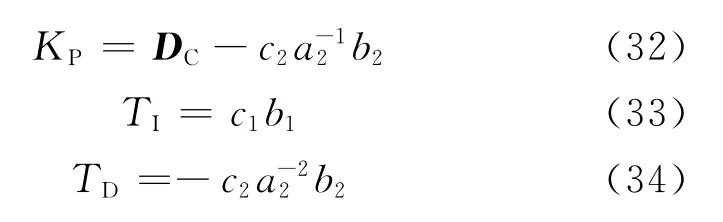
3．3．3 积分纯迟延对象H∞回路成形给定结构控制器设计方法

第三种方法首先需要将标称模型的传递函数近似为带有积分环节加纯迟延的对象

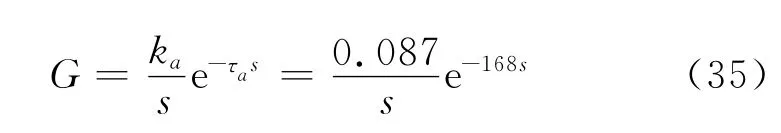
采用积分加纯迟延对象的H∞回路成形控制器经验公式设计方法［7］，若选取比例型权函数

可得到超前滞后单元型控制器，以下简称H∞LSDP公式法一．其控制器结构为

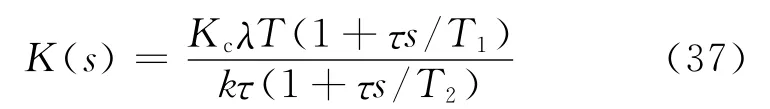
控制器参数整定公式为

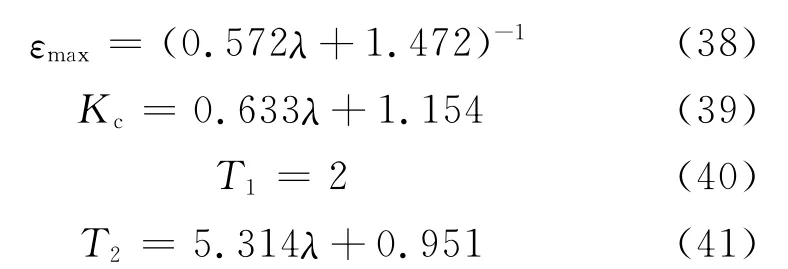
选取积分型权函数

可得到PI串联滤波器型控制器，以下简称H∞LSDP公式法二．其控制器结构为

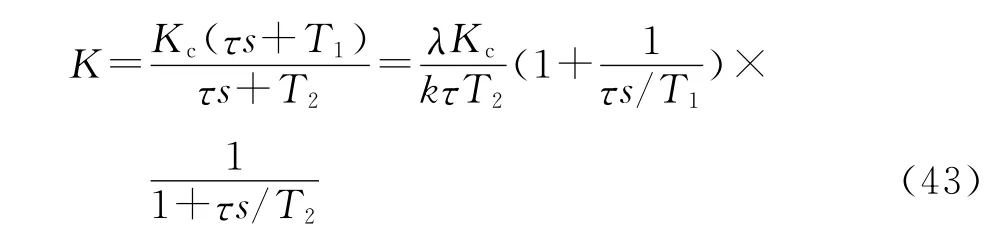
控制器参数整定公式为

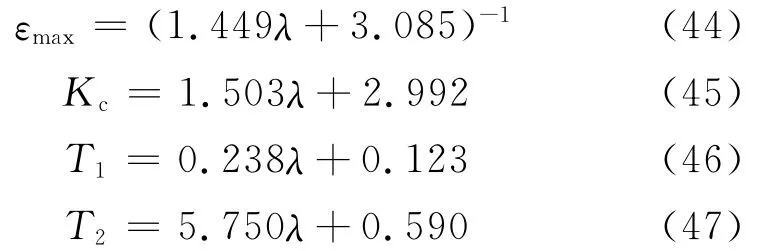
3．4 权函数和控制器参数

上述方法采用的权函数和控制器参数见表2．对于降阶PID，文献［8］中给出的方法所得控制器为理想PID控制器，其控制效果很差，仿真中采用实际微分单元．对于公式法一和公式法二，分别给出了积分加纯迟延近似对象和原对象对应的最大鲁棒裕量εmax．

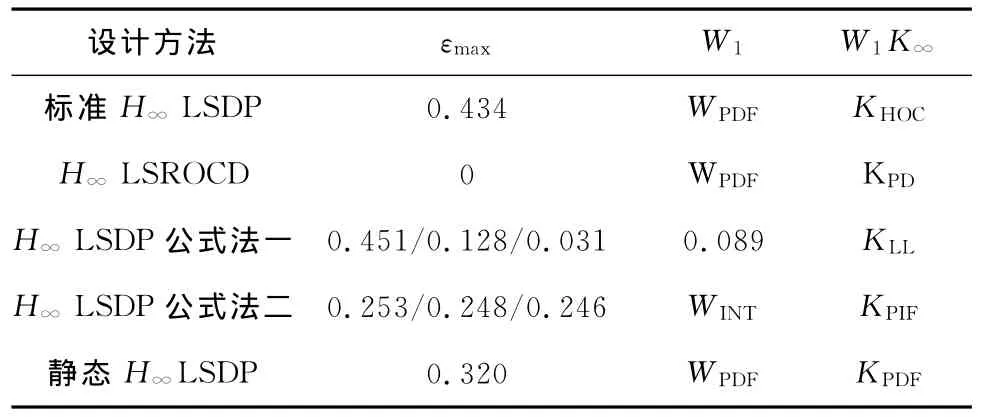
表2 权函数和控制器参数Tab．2 Parameters of weighting function and controller

表2中0．451和0．253表示对简化模型由经验公式一（或经验公式二）计算所得εmax；0．128和0．248表示对简化模型由式（6）计算所得εmax；0．031和0．246表示对标称模型由式（6）计算所得εmax；WPDF和WINT分别为PD串联滤波器型权函数和积分环节型权函数；KPD、KLL、KPIF和KPDF分别为理想PD控制器、超前滞后单元型控制器、PI串联滤波器型控制器和实际PD串联滤波器型控制器的传递函数．

KHOC为9阶控制器，为节省篇幅，此处不给出其状态空间矩阵．仿真中发现KPD控制效果很差，对比试验中采用实际PD控制器KRPD代替，即将理想微分单元更换为理想微分单元串联滤波的形式

由表2可见，标准H∞回路成形所得控制器阶次高达9阶，对应控制系统的εmax却只略大于静态H∞回路成形设计的控制系统的εmax，而静态H∞回路成形所得控制器阶次仅为2阶．

由于拟合误差，对于简化对象Gs，采用经验公式法基于简化被控对象模型所得控制器的实际鲁棒裕量明显小于拟合公式计算所得鲁棒裕量（0．451→0．128，0．253→0．248）；由于拟合误差和建模误差，对于标称对象Gfw，由经验公式法设计所得控制器的鲁棒裕量进一步减小（0．128→0．031；0．248→0．246）；同样，由于拟合误差，降阶PID控制器与标称对象组成的控制系统的鲁棒裕量也显著减小（0．434→0）．因此，基于简化模型，采用经验公式法一、经验公式法二设计所得H∞回路成形控制器以及基于高阶H∞回路成形控制器降阶所得的低阶控制器与实际被控对象组成的控制系统的鲁棒稳定性与鲁棒性能得不到保证．

图3为控制器与成形对象组成的开环系统的幅频特性曲线．由图3可以看出，3种方法设计所得控制器与被控对象组成的开环系统在低频段增益都较低，甚至低于原对象的低频增益，因而抗低频干扰能力较弱．在静态H∞回路成形设计时尝试采用了多种结构的权函数W1，只有超前滞后单元类型以及PD串联滤波器类型的权函数能保证控制器有解；另外，根据MOGA的优化结果，没有同时满足鲁棒裕量大于0．2和低频增益大于10dB的解．

事实上，蒸汽发生器水位对象在低频段存在严重的“收缩膨胀”现象以及很大的惯性和迟延，过大的低频增益很容易导致控制系统发散．另外，由于引入了蒸汽发生器出口蒸汽流量静态前馈，整个控制系统的抗干扰能力得到保证，下面会进一步进行分析．而在核电厂运行过程中，蒸汽发生器水位给定值的改变并不十分频繁，即对给定值变化的跟踪速度没有很严格的要求．

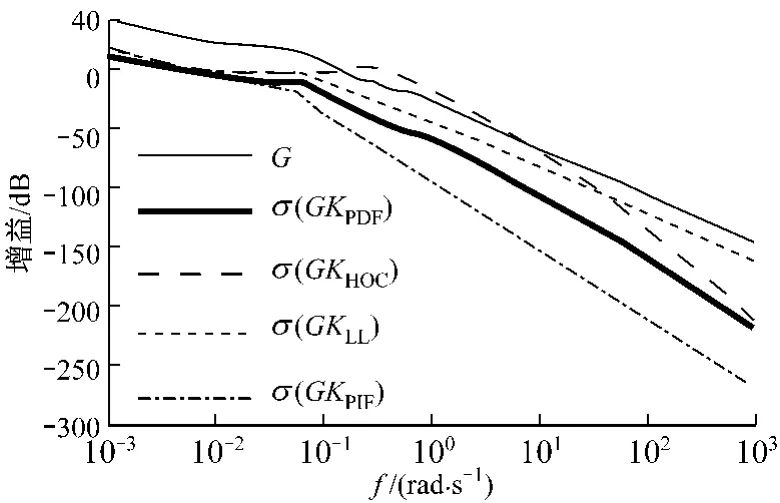
图3 控制器与成形对象组成的开环系统的幅频特性曲线Fig．3 Amplitude frequency characteristics of the open－loop system including the controller and controlled object

静态H∞LSDP与标准H∞LSDP相比，可得到指定结构、容易实现的控制器；与标准H∞LSROCD相比，能保证所得控制器的鲁棒裕量；与H∞LSDP公式法相比，不需拟合被控对象的积分纯迟延型传递函数，且对权函数的阶次和结构没有限制．

4 仿真试验及结果分析

对于低负荷水位控制系统的仿真，在100s加入200mm的水位给定值阶跃变化，1 500s时蒸汽流量增加20kg／s．在5%负荷工况下，4种控制器的控制效果如图4所示．

为了验证所设计控制系统的鲁棒稳定性，采用基于5%负荷标称模型设计所得控制器对15%工况下的水位控制进行了仿真，控制效果曲线见图5（此时标准H∞LSDP所得控制器不能使水位稳定，过渡过程水位振幅很大且逐渐发散，为了保证其他曲线的可读性，图5中没有给出标准H∞LSDP对应的曲线）．

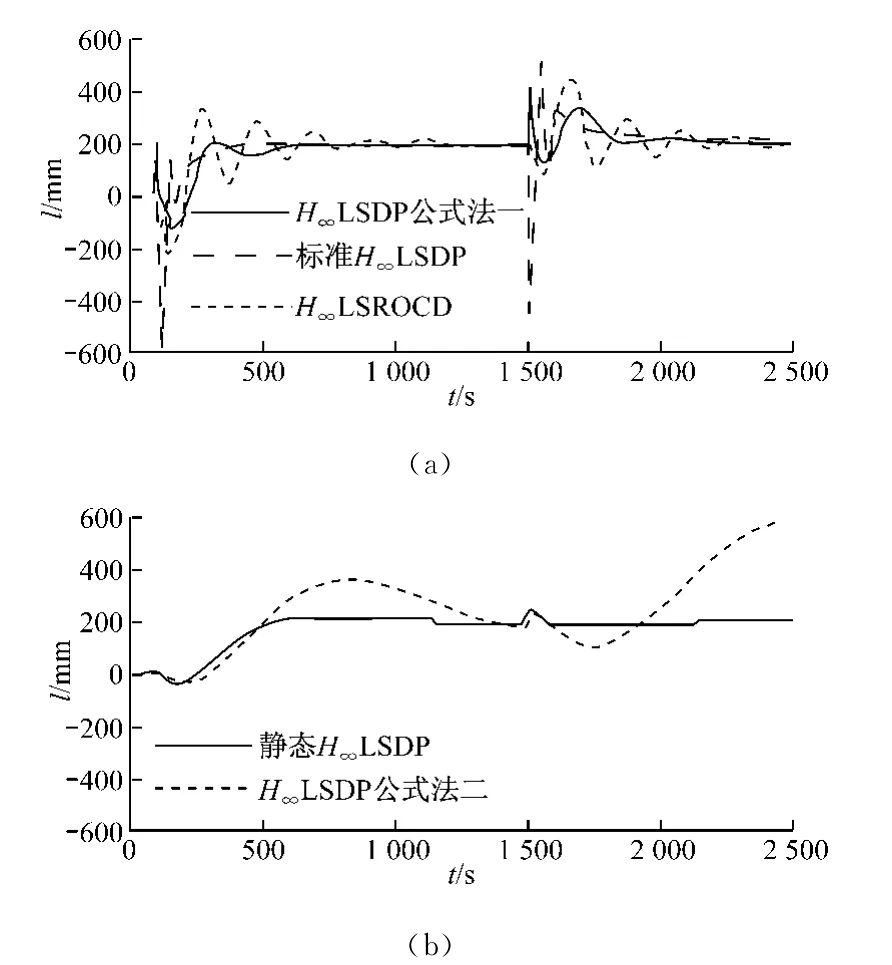
图4 5%负荷下不同控制器的控制效果Fig．4 Control performance of 4controllers at 5%load

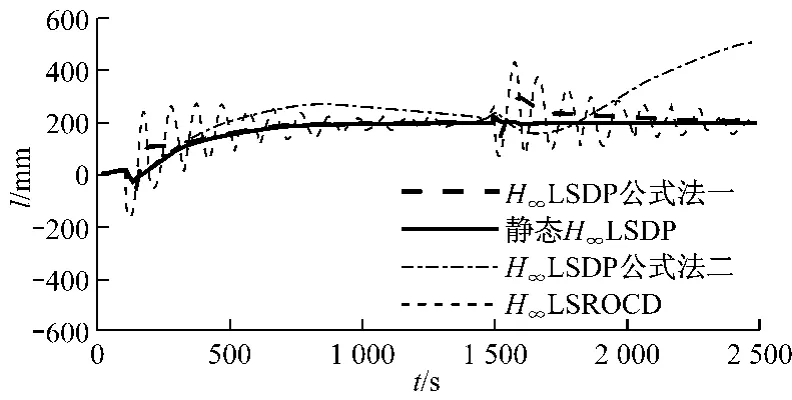
图5 15%负荷下不同控制器的控制效果Fig．5 Control performance of different controllers at 15%Load

考虑到在给水压力波动的情况下阀门的开度－流量特性会发生变化，假定给水压力降低使得阀门流量对象的增益减小一半，惯性时间增加一倍，相应的控制效果曲线见图6（此时标准H∞LSDP所得控制器不能使水位稳定，过渡过程水位振幅很大且逐渐发散，为了保证其他曲线的可读性，图6中没有给出标准H∞LSDP对应的曲线）．假定给水压力升高使得阀门流量对象的增益增大一倍，惯性时间减小一半，相应的控制效果曲线见图7（此时标准H∞LSDP和H∞LSROCD所得控制器不能使水位稳定，过渡过程水位振幅很大且逐渐发散，为了保证其他曲线的可读性，图7中没有给出标准H∞LSDP和H∞LSROCD对应的曲线）．

从图4～图7可以看出，静态H∞回路成形方法设计所得水位控制系统在调节时间、超调量和衰减率等控制指标上均优于其他3种设计方法设计的控制系统．4种控制系统的调节时间均较长，这与图3给出的开环对象奇异值曲线在低频段增益小、穿越频率低相对应．

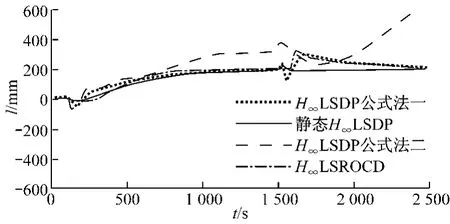
图6 给水压力降低扰动时5%负荷下的控制效果Fig．6 Control performance at 5%load under reduction disturbance of feed water pressure

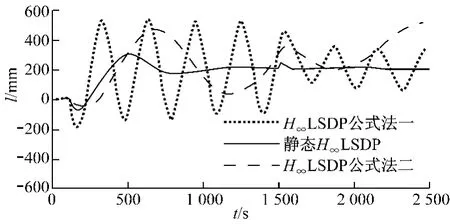
图7 给水压力升高扰动时5%负荷下的控制效果Fig．7 Control performance at 5%load under increase disturbance of feed water pressure

5 结 论

提出一种基于多目标GA权函数参数优化的静态H∞回路成形设计方法．静态H∞回路成形设计能保证所得控制器具有与权函数相同的容易实现的结构，而多目标GA权函数参数优化能使控制器在鲁棒稳定性和频域性能间取得良好的折衷．为了验证所提出方法的有效性，设计了低负荷下蒸汽发生器水位控制系统的PD串联滤波器型控制器．仿真结果表明，所设计的控制器具有良好的鲁棒稳定性和较好的鲁棒性能，综合控制品质优于作为对比的其他3种H∞回路成形方法设计所得控制器．

由于低负荷下蒸汽发生器水位对象显著的“收缩膨胀”效应、大惯性特性和随负荷改变的动力学特性，以及控制器阶次的限制，所设计控制系统的调节时间较长，有待进一步改进．

［1］谷俊杰，米克嵩，徐培培．基于遗传算法的核电站蒸发器高阶水位模型的降阶方法［J］．动力工程学报，2010，30（2）：115－127．GU Junjie，MI Kesong，XU Peipei．Order reduction method of the high order nuclear steam generator level control model based on genetic algorithm［J］．Journal of Chinese Society o f Power Engineering，2010，30（2）：115－127．

［2］米克嵩，谷俊杰，徐培培．内模控制方法在核电厂蒸汽发生器水位系统的应用［J］．核动力工程，2010，31（6）：29－32．MI Kesong，GU Junjie，XU Peipei．Application of internal model adaptive control in water system of nuclear power plant steam generator［J］．Nuclear Power Engineering，2010，31（6）：29－32．

［3］邓志红，施小成，夏国清，等．核电厂蒸汽发生器的容错控制［J］．核动力工程，2010，31（1）：107－111．DENG Zhihong，SHI Xiaocheng，XIA Guoqing，et al．Fault tolerant control for steam generators in nuclear power plant［J］．Nuclear Power Engineering，2010，31（1）：107－111．

［4］陈智，张英，张帆，等．岭澳核电站蒸汽发生器水位控制系统改进方案仿真研究［J］．核动力工程，2010，31（4）：66－70．CHEN Zhi，ZHANG Ying，ZHANG Fan，et al．Simulation study on improvement of steam generator level control system of Ling＇ao nuclear power station［J］．Nuclear Power Engineering，2010，31（4）：66－70．

［5］PATRA S，SEN S，RAY G．Design of static H∞loop shaping controller in four－block framework using LMI approach［J］．Automatica，2008，44（8）：2214－2220．

［6］MCFARLANE D C，GLOVER K．A loop shaping design procedure using H∞synthesis［J］．IEEE Trans AC，1992，37（6）：759－769．

［7］IRVING E，MIOSSEC C，TASSART J．Towards efficient full automatic operation of the PWR steam generator with water level adaptive control［C］／／Proc．2nd Int．Conf．Boiler Dynamics and．Control in Nuclear Power Stations．London：British Nuclear Energy Society，1980：309－329．

［8］张建民．压水堆核电站控制［M］．深圳：广东大亚湾核电站培训中心，1998：113－154．

［9］OSINUGA M，PATRA S，LANZON A．Smooth weight optimization in H∞loop－shaping design［J］．Systems ＆Control Letters，2010，59（11）：663－670．

［10］王海泉，郭迎清，祁新杰．多目标遗传算法在H∞鲁棒控制器设计中的应用［J］．推进技术，2009，30（4）：468－473．WANG Haiquan，GUO Yingqing，QI Xinjie．Multiobjective genetic algorithm applied in H∞robust controller design［J］．Journal of Pro PulSion Technology，2009，30（4）：468－473．

［11］谭文，刘吉臻．典型工业过程的H∞控制［J］．控制理论与应用，1999，16（5）：682－686．TAN Wen，LIU Jizhen．H∞control for typical industrial processes［J］．Control Theory and Applications，1999，16（5）：682－686．