燃煤电厂二氧化硫排放质量浓度的软测量技术

郑海明， 杨 志

（1．华北电力大学 能源动力与机械工程学院，保定071003；2．邢台技师学院，邢台054001）

为了有效控制燃煤电厂SO2排放量，必须及时准确地获取实时数据．现阶段，主要使用的监测设备是烟气连续排放监测系统（Continuous Emission Monitoring System，简称CEMS），该系统对固态污染源颗粒物浓度、气态污染物质量浓度等进行连续监测，并将监测数据信息传送到当地环保局，确保排污企业污染物浓度和排放总量达到国家要求水平［1－2］．同时，脱硫装置也需要依靠 CEMS的数据进行监控和管理，以提高环保设施的效率．在我国大部分坑口电厂，燃烧用煤成分比较稳定，但CEMS设备安装费用比较高，工作环境比较恶劣，并且耗材零件的更换、保养、故障维修和定期的设备检修需要耗费大量的人力、物力和财力．

台湾成功大学曾针对兴达发电厂燃气机组NOx和CO气体的排放建立了预测模型［3］，台湾国立云林科技大学利用倒传递类神经和适应性模糊神经两种方法建立了垃圾焚烧污染物烟气排放质量浓度的软测量模型，测试内容也主要针对NOx排放质量浓度［4］．美国某电厂针对8组往复式引擎设计了一个连续排放监控软测量软件，将近30个变量记录下来并利用硬件的连续排放监测仪器每隔2min取样一次，经过4个多月共取得超过70 000组数据，而最终的连续排放监控软测量系统只使用了7个输入变量，即可计算出NOx及CO的质量浓度［5］．烟气排放的软测量技术（Soft－sensing Technique）研究有着很大的发展空间［6－7］．

1 软测量模型的建立

软测量技术主要依据易测过程变量（称辅助过程变量或二次变量）与待测过程变量之间的数学关系，实现对待测变量的预测分析．软测量模型根据建模方法的不同可以分为2类：基于机理分析的软测量模型和基于辨识建模的软测量模型．

基于机理分析的软测量方法是指运用化学反应动力学和能量平衡等原理，通过对过程对象进行机理分析，找出可测辅助变量与不可测主导变量之间的关系，从而实现对不可测变量的软测量．对于工艺机理比较简单的过程，基于机理建模可以构造出很好的软测量模型．对于复杂的工业过程，完全依赖机理分析建立软测量模型比较困难．

基于辨识建模的软测量方法是把辅助变量和主导变量组成的系统看做一个整体，以辅助变量作为输入端，以主导变量作为输出端，通过现场采集或试验测试，获得过程的输入输出数据，并以此作为依据建立软测量模型．

笔者采用在线辨识建模方法，将燃料状况、锅炉的燃烧状况等作为输入端，二氧化硫排放质量浓度作为输出端，采用神经网络和遗传算法建立软测量模型．下面将具体分析影响SO2排放质量浓度的主要因素和阐述建模过程．

2 SO2排放质量浓度的主要影响因素

以山西大同某坑口电厂的2号机组作为研究对象．图1为该机组锅炉SO2排放质量浓度的CEMS实时监测图．从84h处，锅炉开始停机准备检修，至252h处检修完毕开始发电，由于在锅炉停机状态下，SO2排放质量浓度接近零，所以在前期数据处理过程中，将停机状态的168h部分去除，以剩余328 h工作状况下的数据作为学习样本和测试样本，建立软测量模型．

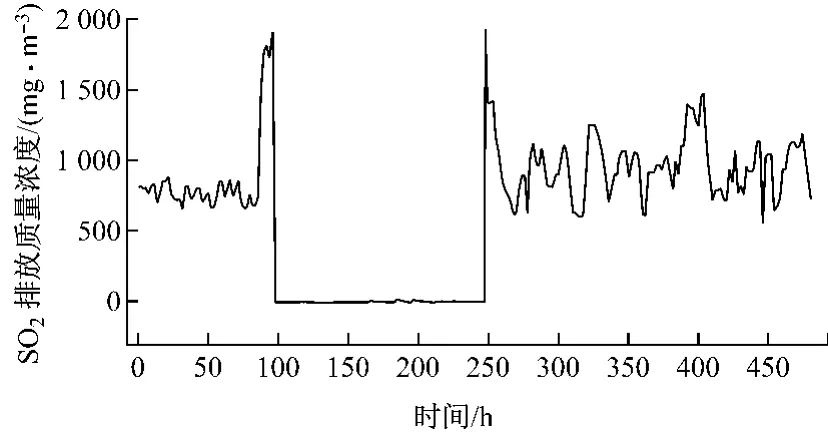
图1 SO2排放质量浓度的实时监测图Fig．1 Real－time monitoring of mass concentration of SO2emission

电厂中影响SO2排放质量浓度的主要因素包括煤中硫质量分数、锅炉负荷、燃烧温度、含氧量、过量空气系数、送风量和给风温度等状态参数［8］．由于该坑口电厂燃烧用煤较稳定，煤的成分含量变化较小，电厂化学检验科室每天采取一定数量的煤样，仅测量一次煤中硫质量分数．为了进行试验数据分析，现对电厂用煤每天进行2次硫质量分数分析，满足建立软测量模型所需要的数据量．图2给出了煤中硫质量分数与SO2排放质量浓度的关系．

图2 煤中硫质量分数与SO2排放质量浓度的关系Fig．2 Mass fraction of sulfur in coal vs．mass concentration of SO2emission

由图2可知，SO2排放质量浓度的变化基本与煤中硫质量分数的变化相对应，煤中硫质量分数的大小是影响SO2排放质量浓度高低的主要因素之一．在100h时，锅炉开始点火启动，当天监测煤中硫质量分数为最高值0．63%．

燃料量变动是锅炉运行中经常遇到的情况．当送入炉膛的煤粉量发生变化时，炉膛内的温度和煤粉在炉内的停留时间都将发生变化，并对燃烧效率产生影响，尤其是负荷很高或很低时，燃烧效率会降低，如果燃用的是低挥发分煤，燃烧损失将会更大，SO2排放质量浓度也会受到很大影响．燃煤锅炉机组的燃烧过程是一个十分复杂的过程，其中风量的大小与含氧量、过量空气系数、燃烧温度和燃烧状况都有直接关联．

从锅炉运行状态到停机过程中，先关闭一次风，停止供给燃料，继续通入二次风，使锅炉内燃料充分燃烧．同理，启机过程中，先通入一次风，后通入二次风．由于这2个状态下燃烧更加充分，SO2排放质量浓度会比平常状态下高．图3给出了SO2排放质量浓度与一次风量和一次风温的对应关系．由图3可知，SO2排放质量浓度的变化基本与一次风量和一次风温的变化相对应．

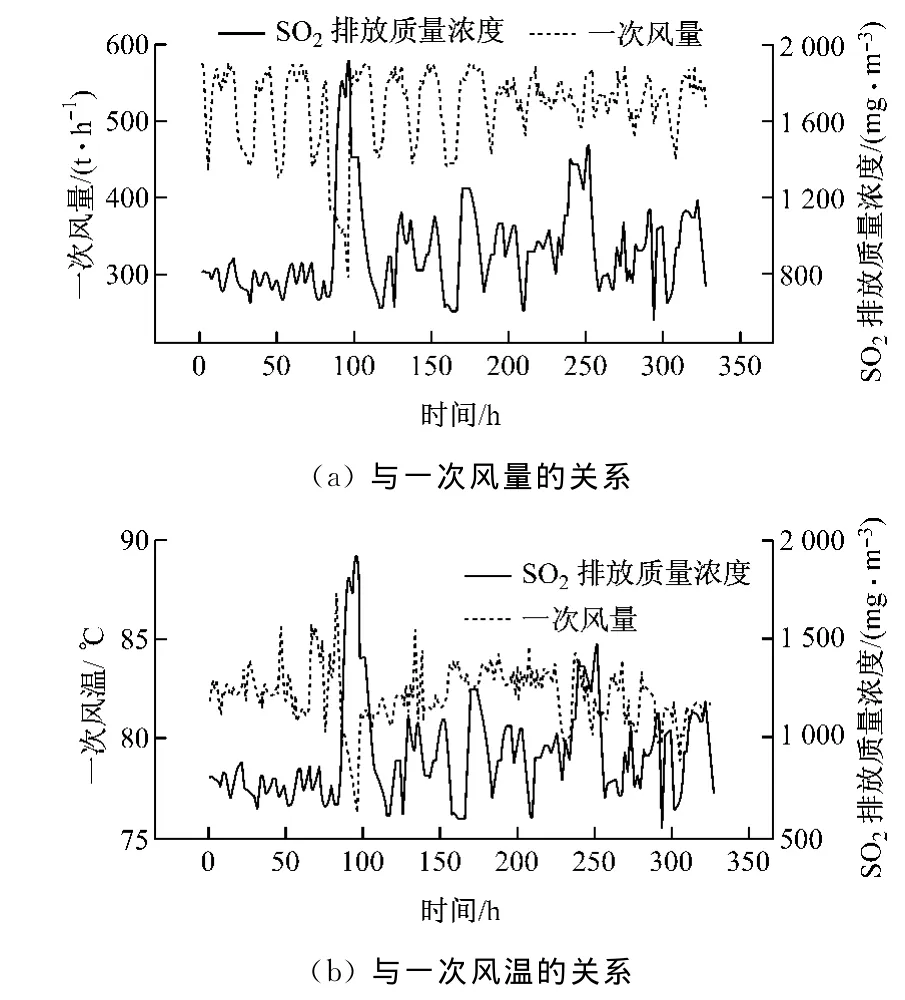
图3 SO2排放质量浓度与一次风温和一次风量的对应关系Fig．3 Mass concentration of SO2emission vs．flow rate and temperature of primary air

3 利用BP网络建立软测量模型

通过上面的简要分析，在燃煤锅炉运行状态下，影响SO2排放质量浓度的主要因素有硫质量分数、锅炉负荷、给煤量、含氧量、过量空气系数、二次风量、二次风温、一次风温、一次风量和排烟温度．笔者选用此10组数据作为BP网络所建立模型的输入变量，以SO2排放质量浓度作为模型的输出变量．

由于输入样本为10维输入向量，而输出变量只有1个，因此输入层共有10个神经元，输出层只有1个神经元．隐含层可以从输入数据中提取特征信息，增加隐含层层数可以提高神经网络的处理能力，但同时也会使神经网络的训练更加复杂化，延长网络的训练时间，本模型使用含有1个隐含层的神经网络．

隐含层节点数对网络模型的精度和训练时间有很大影响．隐含层节点数越多，网络模型的逼近能力越强，但节点数过多会增大模型的训练误差，而且在样本数目有限的情况下，很容易造成过度拟合现象．如果隐含层节点数过少，会使得网络的学习能力变差，无法概括和体现训练中的样本规律．

隐含层节点数大多通过试凑法确定，即先设置较少的节点数，若学习后网络输出误差不符合设定要求，则逐渐增加节点数，直至网络误差不再有明显减少为止．笔者采用如下经验公式确定隐含层节点数：

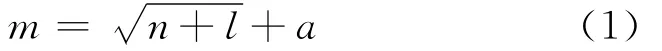
式中：m为隐含层节点数；n为输入层节点数；l为输出层节点数；a为1～10的常数．

经过实践计算得到，当a取10时，即隐含层节点数为14时，训练效果最佳．

由于神经元激活函数的特性，即神经元的输出被限制在（0，1）之间，而期望输出值通常不在这一区间，所以直接用原始数据对根据BP网络建立的软测量模型进行训练将会出现神经元饱和现象，而且数据远离零时，学习速度很慢，误差比较大［9－10］．为了消除上述现象，对输入层的输入样本和输出层的输出样本进行归一化处理，采用式（2）将数据归一化至［0，1］区间内．

式中：xn为归一化后的数据；x0为原始数据；xmax为样本中的最大值；xmin为样本中的最小值．

由于输入层由10维输入向量组成，所以在数据归一化时，各向量需要单独进行归一化处理，然后重新组成输入矩阵．

建立一个10－14－1的3层BP网络软测量模型，然后将归一化后的所有输入输出数据样本的前250组作为训练样本，后78组作为测试样本．图4给出了BP网络预测值与期望输出样本的比较．经过计算得出，预测结果与期望输出样本之间的相对误差率为0．012 7，均方根误差ERMS＝242．246 7．

图4 BP网络预测值与期望样本的对比Fig．4 BP network predicted results vs．expected value of sample information

由图4可以看出，在开始阶段的45h内，预测结果基本与期望值接近，完全满足工程生产的需要，但是在50h、60h和70h附近，预测结果出现了较大幅度的波动，与期望值的偏差增大．综合相对误差率、均方根误差等可以得出以下结论：依据BP神经网络建立的软测量模型基本满足生产需要，但在预测瞬时数据变化激剧时有可能出现一定量的偏差．

通过对51h与50h处样本数据的比较发现，锅炉负荷上升了22．48MW，燃煤量增加了36．49 t／h，其他数据没有大幅度变化，但SO2排放质量浓度却下降了198．36mg／m3，不符合常规情况．经分析，51～55h过程中，燃煤量没有大幅度变化，而SO2排放质量浓度却维持在650～700mg／m3，由此可以推断，在50h处燃料成分出现了一定的波动，如使用硫分较低的煤．

在57～61h和70h附近，输入向量中仅燃煤量的波动与SO2排放质量浓度的波动不相对应，有可能是该时间段中启停某个磨煤机引起给煤量相应变动，从而引起BP网络学习过程中陷入局部极小值，导致预测出错误的数据．

4 遗传算法－BP网络软测量模型

为了提高BP网络软测量模型所遇到误差偏大的问题，引入遗传算法优化网络中的连接权值，搜索一个最优的网络设计方案．本文所建立的软测量模型是根据上一代各层神经元的连接权值的适应性，利用遗传算法的选择、交叉和变异等功能寻求各层神经元之间新的连接权值，反复循环，直至找到最优权值，最终找到输入向量与输出向量之间比较合理的映射关系．

4．1 目标函数的确定

设学习样本xi的网络输出值为yij，期望值为Eij，则可以建立目标函数：

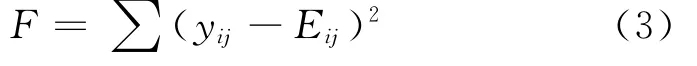
用遗传算法求上述目标函数的极小值，可以得到相对应神经元之间的连接权值．对于一组给定的学习样本，式（3）中yij的大小与神经元之间的连接权值有关，Eij是一个常数．用遗传算法对式（3）进行优化是为了使整个网络中所有权值都对应F的最小值．如果最小值接近零，则表示已经确定了正确的神经网络输入输出关系．

4．2 编码方式

采用实数编码方式，将网络连接权值按照一定的顺序排列成串，串上的每个位置都对应网络的1个连接权值或阈值．L个权值的m个染色体的集合就可以用m行L列数组矩阵A表示，其元素aij是第i个染色体的第j个变量．

编码个体串为（w11，w12，…，b1，w21，w22，…，wij，bi，…），其中wij是神经元j到神经元i的连接权值，bi是神经元i的阈值．选取10－14－1的3层神经网络结构，神经网络的连接权值为10×14＋14＝154个，阈值为14×1＋1＝15个，个体串长度L＝154＋15＝169，初始种群取10．

4．3 适应度函数

遗传算法的适应度函数是遗传算法指导搜索的唯一信息，其选取是算法好坏的关键．适应度函数要指导搜索沿着优化参数组合的方向逐步逼近最佳参数组合，而不会导致搜索不收敛或者陷入局部最优解．函数也要易于计算，适应度函数值在［0，1］区间内，越接近1的个体，其输出信号的正确率就越高．适应度函数的设计应满足下列条件：合理、一致性；单值、连续、非负、最大化；通用性强；计算量小．

fi为个体i的适应度，用误差平方和E衡量．

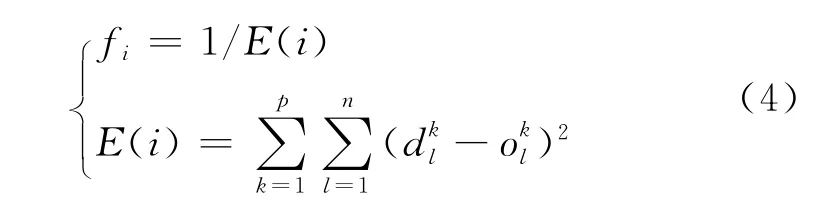
式中：k为学习样本数；l为输出层节点数；dl为网络的实际输出；ol为期望输出．

4．4 遗传操作的设定

选择操作：采用轮盘选择法，基于适应度比例的选择策略．对个体i的选择概率Pi为

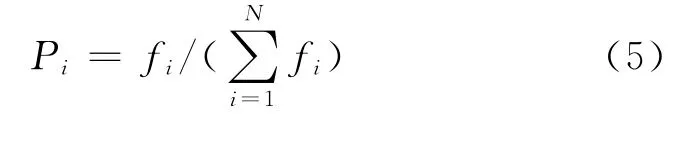
交叉操作：交叉率Pc的自适应调整函数为

式中：fc为交叉父代2个个体中适应度大的个体的适应度；f－为种群的平均适应度；fmax为最大适应度．变异操作：变异率Pm的自适应调整函数为

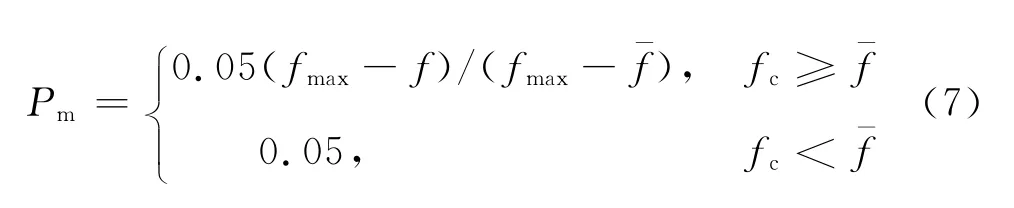
式中：f为需变异个体的适应度．

通过对遗传算法和BP神经网络耦合模型进行训练，蚁群算法经过50次迭代运算后，适应度满足需求．图5为遗传算法－BP神经网络预测结果的拟合曲线．由图5可知，基于遗传算法－BP神经网络建立的软测量回归模型的预测值和真实值的效果点主要分布在对角线两侧，并向对角线逼近，表明训练的测试样本有较好的回归预测性能．

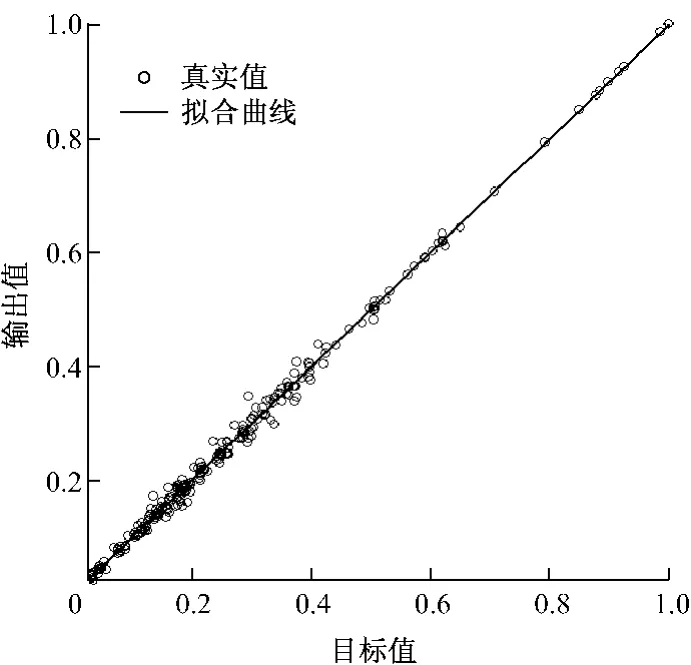
图5 遗传算法－BP神经网络预测结果的拟合曲线Fig．5 Fitting curve of BP network predicted results based on genetic algorithm

图6给出改进后的软测量模型SO2排放质量浓度的预测值与期望样本数据之间的对比．经过遗传算法优化连接权值后的神经网络软测量模型的预测精度非常高，预测值与期望样本之间的偏差较小，而且在50～51h、57～61h和67～75h时间段，预测得到的SO2排放质量浓度并没有出现较大波动．

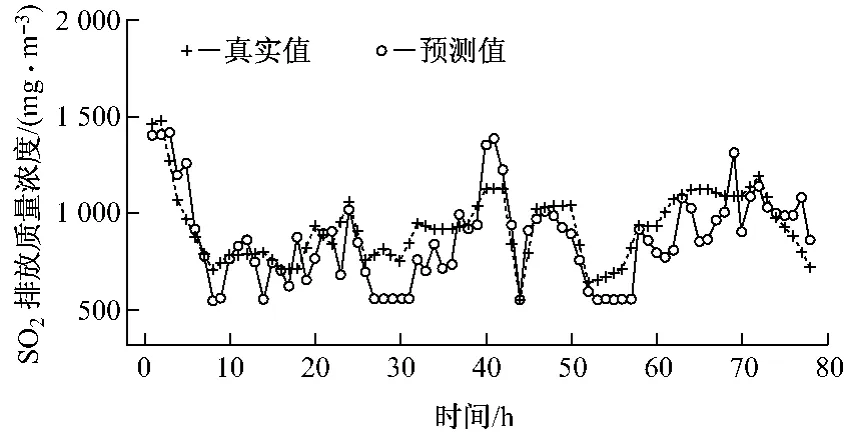
图6 遗传算法－BP网络预测值与期望样本的比较Fig．6 BP network predicted results based on genetic algorithm vs．expected value of sample information

改进后的软测量模型预测结果与期望输出样本之间的相对误差率为0．006 1，减小了近一半，均方根误差ERMS＝160．014 3，与单纯的BP神经网络软测量模型相比也有了大幅度的下降．

5 结 论

（1）经过遗传算法优化连接权值的BP神经网络模型能够满足在线监测要求，可以及时、准确地将数据反馈给电厂工作人员．

（2）与单纯的BP神经网络模型相比，改进的软测量模型在收敛速度和精度方面都有很大的提升，证明了算法的高效性和较强的泛化能力．

（3）实现了在燃料煤粉成分比较稳定的坑口火电厂中SO2排放量的预测．

［1］环境保护部科技标准司．烟尘烟气连续自动监测系统运行管理［M］．北京：化学工业出版社，2008．

［2］郑海明，蔡小舒．烟气连续排放监测系统计量相对准确度测试评估［J］．计量学报，2007，28（1）：85－88．ZHENG Haiming，CAI Xiaoshu．Relative accuracy test evaluation for flue gas continuous emission monitoring systems［J］．ACTA Metrologica Sinica，2007，28（1）：85－88．

［3］CHIEN T W，CHU H，HSU W C，et al．A performance study of PEMS applied to the Hsinta power station of Taipower［J］．Atmos Environ，2005，39（2）：211－222．

［4］陈建谷．应用倒转类神经及适应性模糊类神经网络模式预测垃圾焚化厂烟道气之比较研究［D］．台湾：台湾国立云林科技大学，2003．

［5］GOODWIN G C．Predicting the performance of soft sensors as a route to low cost automation［J］．Annual Reviews in Control，2000，23（4）：55－66．

［6］梁森，李凌．电站锅炉低NOx排放的参数辨识［J］．动力工程，2006，26（5）：68－73．LIANG Sen，LI Ling．Parametric identification of low NOxemitted by power station boilers［J］．Journal of Power Engineering，2006，26（5）：68－73．

［7］丁艳君，吴占松．锅炉烟气排放检测软件传感器 ［J］．清华大学学报：自然科学版，2002，42（12）：1636－1638．DING YanJun，WU Zhansong．Software sensors for boiler emission monitoring ［J］．Journal of Tsinghua University：Science and Technology，2002，42（12）：1636－1638．

［8］罗陨飞，陈亚飞，姜英．燃煤过程硫排放与煤质特征的关系研究［J］．煤炭科学技术，2005，33（3）：61－63．LUO Yunfei，CHEN Yafei，JIANG Ying．Study on relationship between sulfur emission during coal combustion and coal characteristics［J］．Coal Science and Technology，2005，33（3）：61－63．

［9］赵珊珊，白焰．神经网络模糊多模型软测量在磨煤机存煤量测量方面的应用［J］．动力工程学报，2011，31（10）：745－750．ZHAO Shanshan，BAI Yan．Application of fuzzy multi－model soft sensor in mill load measurement based on neural network［J］．Journal of Chinese Society of Power Engineering，2011，31（10）：745－750．

［10］陈鸿伟，刘焕志，李晓伟．双循环流化床颗粒循环流率试验与BP神经网络预测［J］．中国电机工程学报，2010，30（32）：25－29．CHEN Hongwei，LIU Huanzhi，LI Xiaowei．Experimental research on solids circulation rate in a double fluidized bed and BP neural network prediction［J］．Proceedings of the CSEE，2010，30（32）：25－29．