基于非线性滤波环节的新型鲁棒PID控制策略的研究

李 军， 万文军， 张 曦

（广东电网公司电力科学研究院，广州510080）

鲁棒特性较好的PID控制策略在工业过程控制领域中占主导地位，为提高热工对象的控制品质，在调节回路中加入微分环节是工程实践中常采用的典型方法之一．然而，微分环节在改善系统动态性能的同时，其高通滤波特性却放大了高频干扰，往往使微分环节的超前校正作用难以实现，甚至在有外部高频干扰时容易造成系统调节机构大幅波动［1］．而且，随着过程特性及操作条件的改变，PID控制系统难以继续保持良好的控制品质．因此，鲁棒PID控制器的设计受到了广泛的关注．针对多模型不确定对象，Ge等［2］提出一种基于LQR－LMI的鲁棒PID控制器设计方法；Goncalves等［3］提出一种鲁棒两自由度PID控制器设计方法，以满足闭环系统的H2／H∞性能指标；Kim等［4］提出一种基于扩展Lagrange粒子群算法的鲁棒PID控制器设计方法，来满足多个H∞性能指标；刘建民等［5－8］也都提出了各具特色的鲁棒PID控制器设计方法．但这些方法均存在算法复杂，在DCS中较难实现的问题．

针对以上问题，将非线性滤波环节与传统的PID控制策略相结合［1］，提出了一种基于非线性滤波环节的新型鲁棒PID控制策略，该控制策略算法简单，易于实现，提高了传统PID控制策略的鲁棒性，且控制回路能获得优良的控制品质．

1 非线性滤波环节的构造与分析

控制系统的频域特性分析方法是控制系统设计、性能分析、参数调整的基本方法［9－11］，该方法的特点是易于理解．因此，笔者主要从频率特性角度进行计算与分析．

1．1 非线性滤波环节构造图

图1为非线性滤波环节的构造图，非线性滤波环节由二阶微分环节非线性压缩模块、预失真模块、非线性信号重整模块、一阶惯性模块等构成．各模块的作用如下：

（1）二阶微分环节非线性压缩模块：采用平方根特性对二阶微分环节输出信号进行非线性压缩．

（2）预失真模块［12］：对输入信号进行非线性预处理，按预定的（平方根特性）规律产生失真．

（3）非线性信号重整模块：对二阶微分环节非线性压缩模块、预失真模块输出信号进行重整，其作用为进行非线性补偿，对于正弦波或余弦波函数，理论上非线性补偿后的失真为零．另外，该模块还可以保证输出信号与输入信号之间成比例变化．

（4）一阶惯性模块：对非线性信号重整模块的输出进行一阶惯性滤波．

图1 非线性滤波环节的构造Fig．1 Structure of the non－linear filter link

1．2 非线性滤波环节频域特性分析

图1中二阶微分环节所对应的频域函数表达式如下：

令s＝ωj，得到相应的频域函数表达式为：

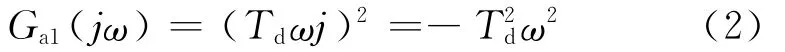
对上述二阶微分环节信号进行带符号开根号运算，其带符号开根号的定义为：

为不失一般性，假设回路的输入信号是幅值为A，角频率为ω的正弦波信号，即输入信号为X（t）＝Asin（ωt）．结合式（2）和式（3），该正弦波信号的二阶微分值带符号开方等式为：

对过程输入信号进行绝对值开根号运算，获得非线性预失真信号，得到相应的过程函数表达式为：

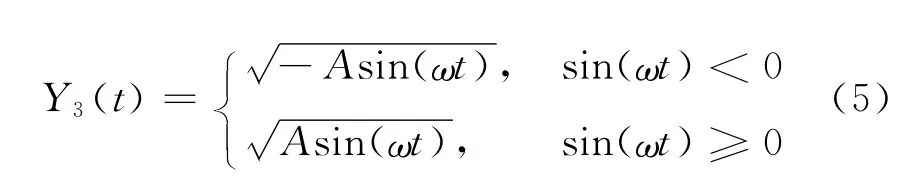
将二阶微分信号的非线性压缩信号与非线性预失真信号相乘，获得非线性重整信号，得到相应的过程函数表达式为：经过非线性重整后的信号与输入信号传递的频域函数为：

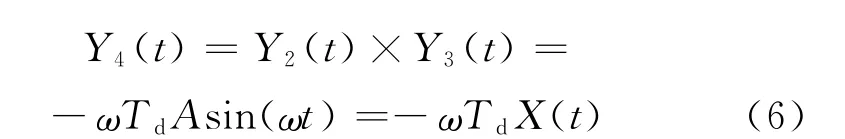
式（7）也可表达为：

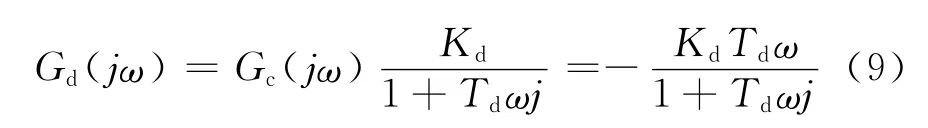
式（9）也可表达为：

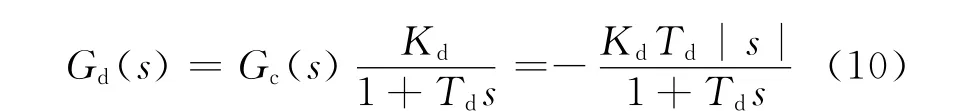
将式（9）的频域函数进行分母有理化得到式（11）

为方便分析，令增益Kd＝1，则实数项为虚数项为实数项和虚数项对应的幅值－频率特性数学计算结果见图2（其中Kd＝1、ωo＝1／Td）．

从图2可以看出，实数项（图2中实线）对应的幅频特性具有典型的带通滤波特性，等价为一带通滤波器，负值表示反相位．虚数项（图2中虚线）对应的幅频特性具有典型的高通滤波特性．实数项和虚数项的这种特性与实际微分环节的幅值特性存在本质区别．

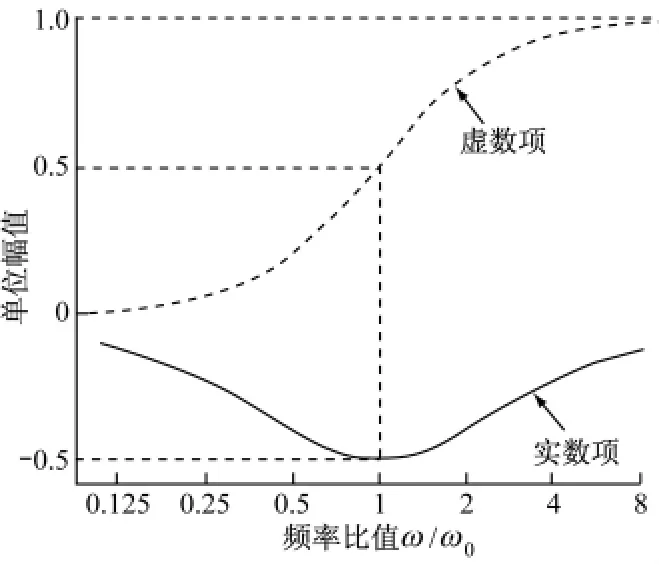
图2 非线性环节幅频特性分析Fig．2 Frequency－domain characteristic analysis of the non－linear filter link

2 非线性鲁棒PID控制策略

为了验证上述方法的有效性，进行了大量仿真试验．非线性滤波环节结合传统PID控制策略的仿真试验方框图见图3，其中取非线性滤波环节的参数与微分环节相同，仿真对象为6阶惯性等容对象．对应的开环传递函数为：

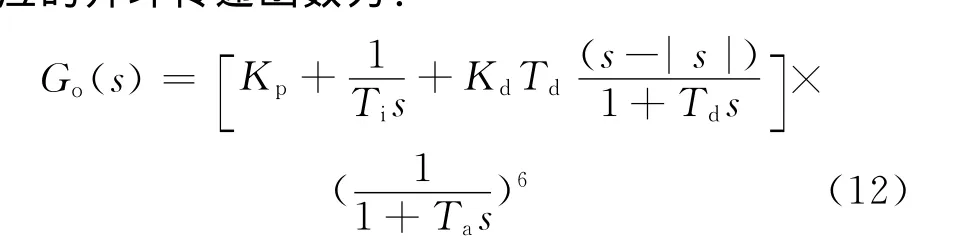
闭环传递函数为：

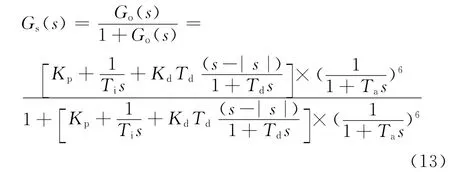
2．1 非线性滤波环节提高系统鲁棒性的定性分析

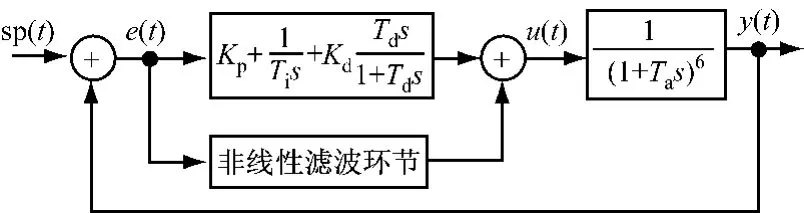
图3 鲁棒PID控制策略仿真框图Fig．3 Block diagram of proposed robust PID control strategy for simulation

经典控制理论的Nyquist稳定性判据是通过确定性开环系统P（s）的频率特性进行的，控制系统的鲁棒性能分析则是通过不确定开环系统P（s）的频率特性进行的．理论上，系统稳定性是由开环系统稳定性裕量决定的．而热工控制系统稳定性裕量又主要由系统在中频段的特性决定，中频段是指系统增益为0dB附近的一段频率．在对象确定以后，系统稳定性裕量便由PID控制器中频段输出超前虚频幅值与实频幅值特性决定．

理论与实践经验表明，对于高阶被控对象，相应的PID调节器回路的响应速度与稳定性之间存在矛盾．而非线性滤波环节提高系统鲁棒性的原理在于：非线性滤波环节既能够较大幅度地降低PID控制器中频段输出实频幅值，又能够较大幅度地提高PID控制器高中频段输出超前虚频幅值，在较大幅度提高PID调节器回路响应速度的同时又具有较高的稳定性，较好地解决了PID调节器回路的响应速度与稳定性之间的矛盾．

2．2 非线性滤波环节提高稳定性裕量的定量分析

对于图3给出的仿真图，具体参数见3．1节，其开环调节器对应的实频和超前虚频输出特性曲线见图4和图5．选择非线性滤波环节参数的原则是使实数项的峰值出现在系统频率特性的中频段范围，这样就能够较大幅度地降低调节器在中频段输出实频幅值，具体见图4．非线性滤波环节中的虚数项能够较大幅度地提高调节器在中高频段输出超前虚频幅值，具体见图5所示（正值为超前、负值为滞后）．

图4 2种控制系统开环调节器输出实频对比图Fig．4 Output comparison of open loop system between traditional PID and robust PID（R）

图6为2种控制系统开环频率特性对比图．由图6可知，在加入非线性滤波环节后，相位稳定裕量从70°略微下降到69．5°，可认为几乎没有变化．然而，幅值稳定裕量从6dB提高到10．2dB，可见非线性滤波环节可以明显提高开环系统稳定性裕量．

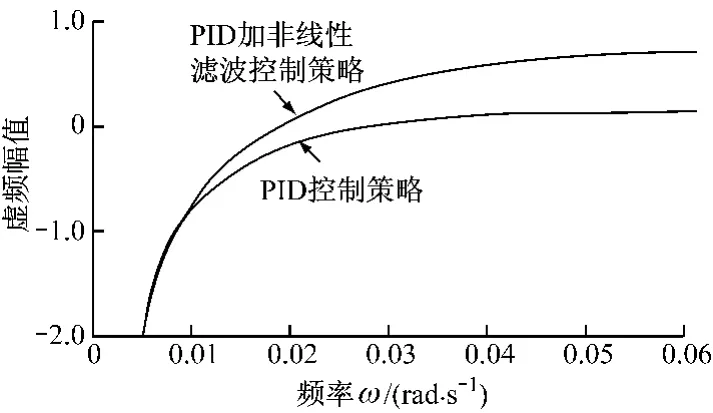
图5 2种控制系统开环调节器输出虚频对比图Fig．5 Output comparison of open loop system between traditional PID and robust PID （I）

图6 6阶惯性等容仿真对象的2种控制系统开环频率特性对比图Fig．6 Comparison of open－loop frequency characteristics between two control systems by 6－order inertial isovolumetric simulation

由图6还可以看出，在相位稳定裕量判定点频率和幅值稳定裕量判定点频率范围内，系统开环频率特性幅频增益显著下降，相频相位滞后值显著下降，即开环对象滞后特性得到了改善．此外，在加入非线性滤波环节后，2个稳定裕量判定点对应的频率宽度B2比未加入非线性滤波环节前2个稳定裕量判定点对应的频率宽度明显增加，这意味着鲁棒性提高了．原因在于：在临界稳定状态，2个稳定裕量判定点频率相等，其对应的频率宽度为零．而在临界稳定边界以内，2个稳定裕量判定点之间的频率宽度越大，其适应不确定开环系统P（s）频率特性变化的范围也越大．当图3中仿真惯性等容对象的阶数从6阶增加到12阶时，得到的2种控制系统开环频率特性的对比见图7．

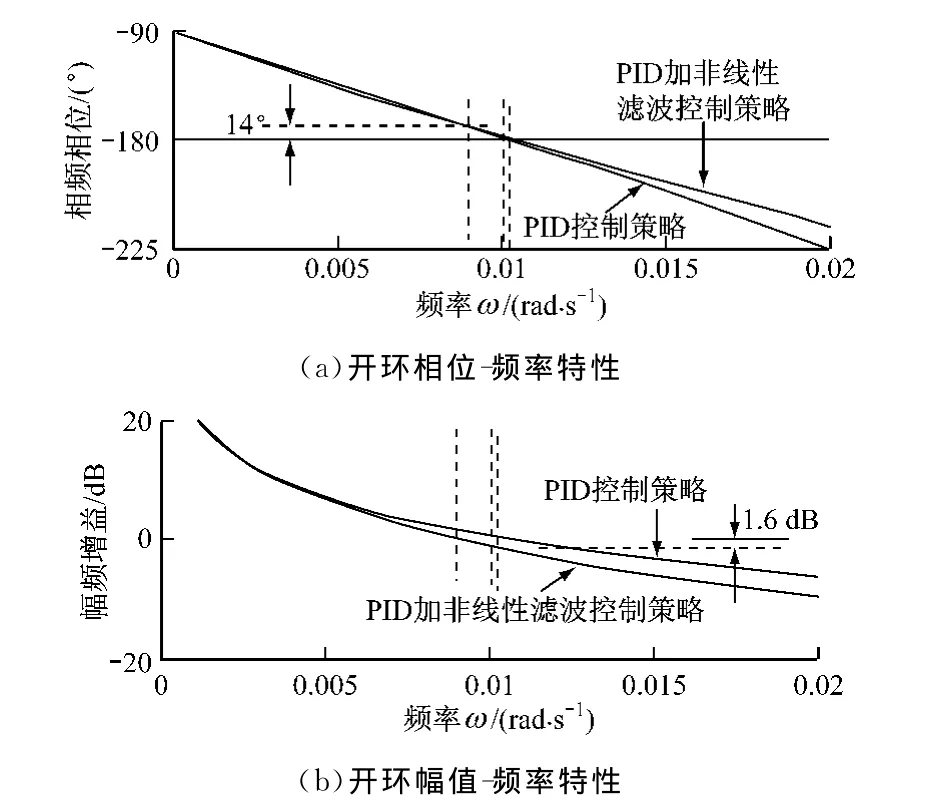
图7 12阶惯性等容仿真对象的2种控制系统开环频率特性对比图Fig．7 Comparison of open－loop frequency characteristics between two control systems by 12－order inertial isovolumetric simulation

由图7可知，未加入非线性滤波环节时的相位稳定裕量和幅值稳定裕量几乎为零，可认为已处于临界稳定状态，而加入非线性滤波环节后的相位稳定裕量为14°、幅值稳定裕量为1．6dB，仍处于临界稳定边界内．

非线性滤波环节必须与微分环节联合使用，单独使用非线性滤波环节的效果并不理想．例如对某些具体的实际过程系统，如果通过简单提高系统响应速度就能较好地解决问题，则应用非线性滤波环节可起到良好的效果．对于系统来说，通过微分作用可提高系统响应速度，通过非线性滤波环节可充分保证系统稳定性，将非线性滤波器与传统PID联合使用的控制方法称为新型鲁棒PID控制器．下面的仿真将充分说明该PID控制回路的特性．

3 仿真研究

3．1 阶跃响应仿真

选取仿真对象为6阶惯性等容对象，对应的时间常数为Ta＝20s．依据传统PID参数整定原则得到控制器参数为：Kp＝0．85、Ti＝95s、Kd＝0．75、Td＝33s，并取非线性滤波环节中的参数等于PID中的微分参数Kd＝0．75、Td＝33s．

将提出的鲁棒PID控制策略与传统PID及PI控制策略进行了对比分析，系统的阶跃响应曲线见图8．从图8可以看出，鲁棒PID控制策略调节效果良好，与传统方法相比具有更大的稳定裕量．

由图8还可以看出，采用非线性滤波环节的PID控制策略后，其调节上升速率和超调量方面的品质均优于传统PID控制策略．另外，在提高响应速度后，采用非线性滤波环节可以充分保证调节回路的稳定性．可见加入非线性滤波环节后，允许PID参数的调整范围更宽，一定程度上增强了控制回路的鲁棒性．

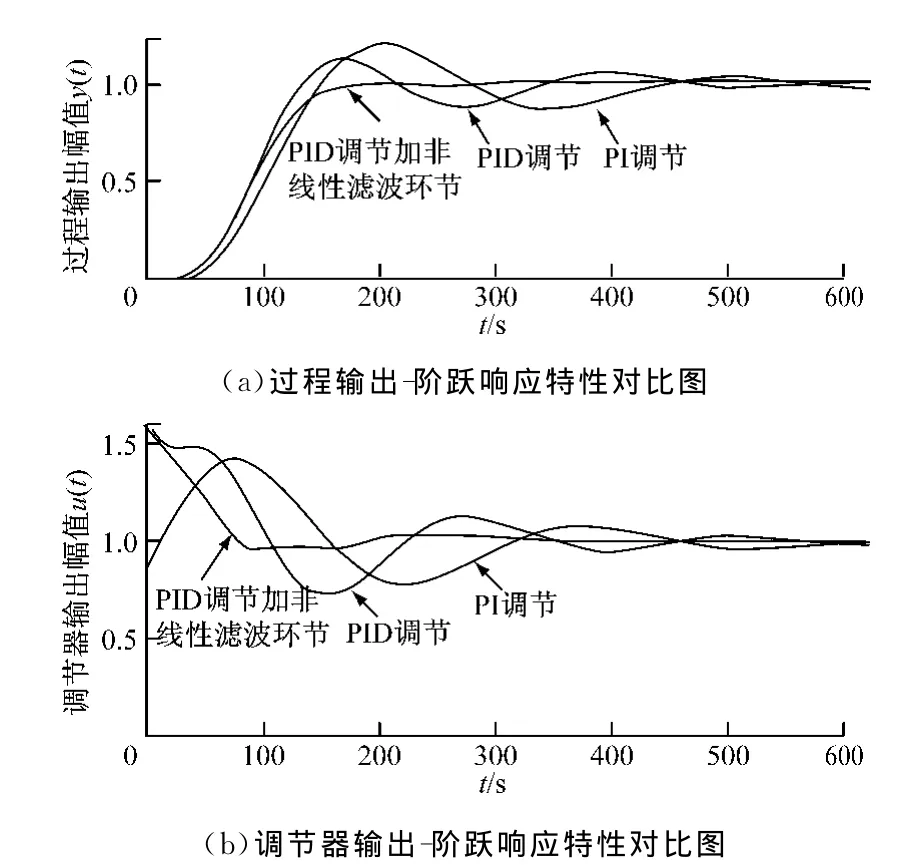
图8 3种控制策略阶跃响应仿真结果的对比Fig．8 Comparison of simulation results among robust PID，PI and traditional PID

3．2 400s方波响应仿真

为了进一步说明所提出方法的有效性，对系统进行了400s方波响应测试，得到的响应曲线见图9．从图9可以看出，所提出的控制策略抗扰动能力较强，具有更为优良的控制特性．

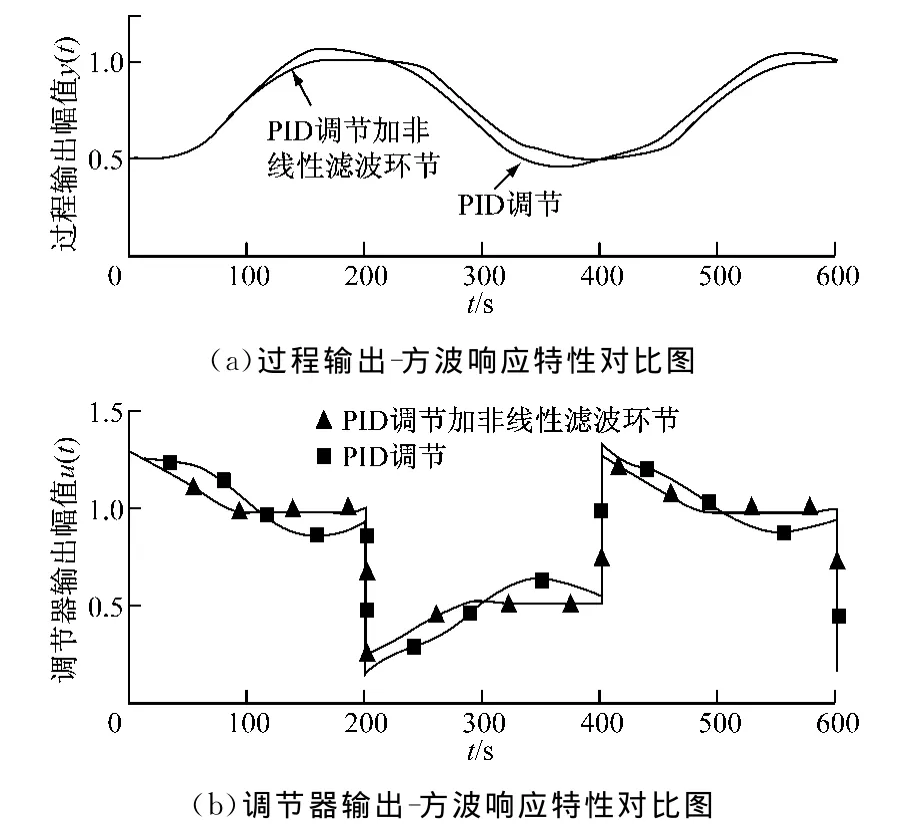
图9 2种控制策略400s方波响应仿真结果的对比Fig．9 Comparison of 400ssquare wave response between robust and traditional PID

4 工程应用

将提出的非线性滤波环节应用于某660MW机组的汽包锅炉过热汽温调节系统中，该锅炉过热汽温调节系统仅有一级调节．优化前，锅炉过热汽温调节系统采用的是常规PID控制策略，系统的过程量在变负荷过程中经常发生较大幅度的波动．为此，在原有的主控回路中引入本文提出的非线性滤波环节，并且较大幅度地提高主控PID的比率增益（提高30%）和微分增益（提高40%），系统仍然很稳定．投运效果表明：引入非线性滤波环节后，系统调节品质得到了明显提高，变负荷过程过热汽温动态波动范围有较大幅度降低，其中B侧过热汽温调节系统优化前后对比如图10所示．

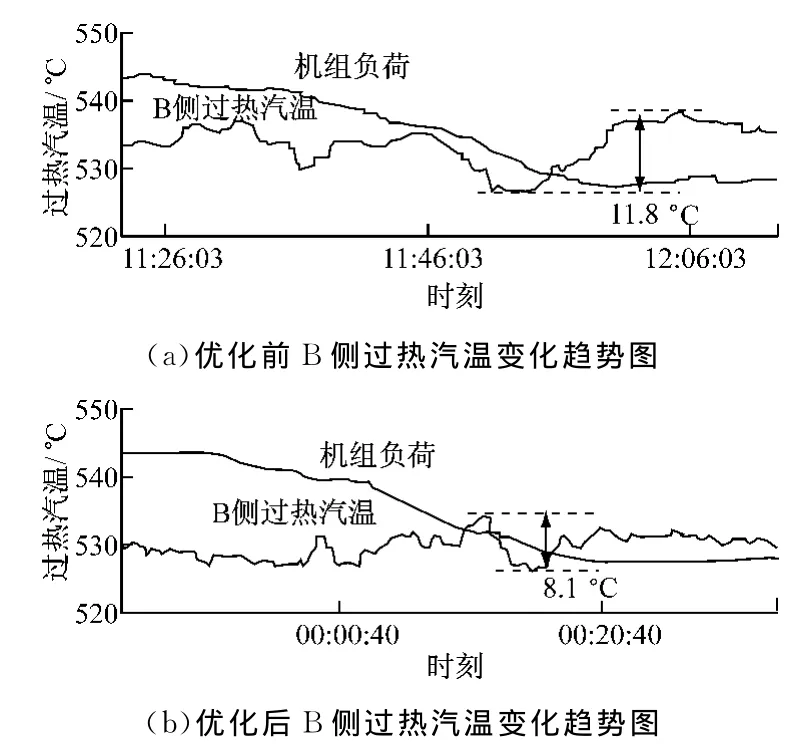
图10 B侧过热汽温调节系统优化前后过热汽温变化趋势图Fig．10 Temperature variation of B－side superheated steam before and after optimization

从图10可以看出，优化前，汽温变化速率较慢，趋势虽然比较平滑，但汽温上下波动幅度较大，其中的一个原因在于PID调节回路响应速度较慢．曾经尝试提高PID调节回路的响应速度，但调节回路的稳定性显著变差．采用本文提出的非线性滤波环节进行优化后，在较大幅度提高PID调节回路响应速度的同时又具有较高的稳定性，对抑制变负荷过程中汽温波动的效果显著．通过对比分析实际应用效果，进一步证实了本文提出方法的优越性．

5 结束语

提出了一种基于非线性滤波环节的新型鲁棒PID控制策略，并对非线性环节的频域特性进行了深入分析，给出了滤波环节提高系统鲁棒性的原理．通过将非线性滤波环节与传统PID控制相结合，较大程度提高了传统PID控制策略的鲁棒性，获得了良好的控制品质，在提高系统响应速度的同时也提高了系统的稳定性．阶跃扰动、方波扰动仿真试验以及对象特性变动后鲁棒性分析及实际应用效果验证了该策略的有效性．

［1］李军．基于改进微分环节的控制策略的研究及其应用［J］．热力发电，2010，39（8）：72－75．LI Jun．Study on new type control strategy based on improved differential link and application thereof［J］．Thermal Power Generation，2010，39（8）：72－75．

［2］GE M，CHIU M S，WANG Q G．Robust PID controller design via LMI approach［J］．Journal of Process Control，2002，12（1）：3－13．

［3］GONCALVES E N，PALHARES R M，TAKAHASHI R H C．A novel approach for H2／H∞robust PID synthesis for uncertain systems［J］．Journal of Process Control，2008，18（1）：19－26．

［4］KIM T H，MARUTA I，SUGIE T．Robust PID controller tuning based on the constrained particle swarm optimization［J］．Automatica，2008，44（4）：1104－1110．

［5］韩恺，赵均，朱豫才，等．一种扰动自适应的鲁棒预测控制算法［J］．化工学报，2009，60（7）：1730－1738．HAN Kai，ZHAO Jun，ZHU Yucai，et al．A robust MPC technique with adaptive disturbance model［J］．CIESC Journal，2009，60（7）：1730－1738．

［6］勒其兵，叶琼瑜，赵大力．一种改进的鲁棒分散PID控制器的设计［J］．系统仿真学报，2009，21（3）：780－783．JIN Qibing，YE Qiongyu，ZHAO Dali．Modified robust decentralized PID controllers design［J］．Journal of System Simulation，2009，21（3）：780－783．

［7］王传峰，李东海，姜学智，等．基于概率鲁棒性的锅炉过热汽温串级PID控制器［J］．清华大学学报：自然科学版，2009，49（2）：249－252．WANG Chuanfeng，LI Donghai，JIANG Xuezhi，et al．Cascade PID controllers for superheated steam boiler temperatures based on probabilistic robustness［J］．J Tsinghua Univ：Science and Technology，2009，49（2）：249－252．

［8］刘建民，韩璞，开平安，等．一种改进的α－β－γ滤波器和PID控制器［J］．动力工程，2007，27（4）：551－554．LIU Jianmin，HAN Pu，KAI Pingan，et al．An improvedα－β－γfilter and PID controller［J］．Journal of Power Engineering，2007，27（4）：551－554．

［9］THAM M T．Why frequency response［R］．Australia：University of Newcastle upon Tyne，1999：1－17．

［10］WANG Yagang，CAI Wenjian，GE Ming．Decentralized relay－based multivariable process identification in the frequency domain［J］．IEEE Trans On Automatic Control，2003，48（5）：873－877．

［11］李军，万文军，张曦．一种基于阶跃响应的理想频率信号源及频域分析的研究［J］．动力工程学报，2012，32（4）：308－314．LI Jun，WAN Wenjun，ZHANG Xi．Study on ideal frequency signal source based on step response and its utility in frequency domain analysis［J］．Journal of Chinese Society of Power Engineering，2012，32（4）：308－314．

［12］张玉兴，赵宏飞，向荣，等．非线性电路与系统［M］．北京：机械工业出版社，2007：183－185．