二射影对应面束与二次曲面
2013-09-21刘阜平
刘阜平, 丁 勇
(太原理工大学,山西 太原 030024)
椭圆、抛物线和双曲线,可以通过同一对对应的二射影线束相对运动来形成[1]。与其相对应,椭圆柱面、抛物柱面和双曲柱面,也可以通过同一对对应平行的二射影面束相对运动来形成。那么圆锥面、单叶双曲面和双曲抛物面呢?我们都知道,斜椭圆锥面无轴线[2],是否有圆截口?如果没有圆截口,原因是什么?为什么单叶双曲面[3]的截交线是抛物线、双曲线和椭圆,与圆锥面的截交线种类相同?这些问题都可以通过对二射影对应面束的相对运动,合同线束所在截平面位置等问题的讨论来回答。
1 二射影对应面束的两对合同线束作图法
如图 1所示,二射影对应面束l1(A1α,B1α,C1α…),l2(A2α,B2α,C2α…),如果分别取垂直于底l1l2的平面T1αT2α截切,得到对应线束L1(a1,b1,c1…),L2(a2,b2,c2…),如果l1l2平行,移动共底后二线束L1L2成椭圆形对合,也就是二面束l1l2成椭圆形对合。如图2所示,二线束L1L2的两对主直线m1m2和n1n2两对“等角线”x1x2和y1y2以及反映二线束度量性的α角与二面束相对应。
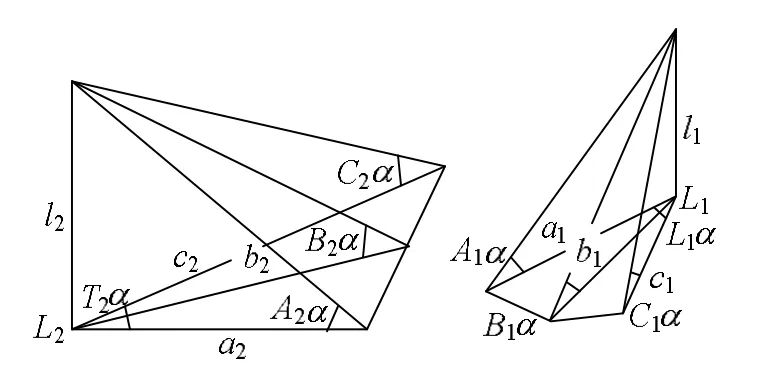
图1 二射影对应面束示意图
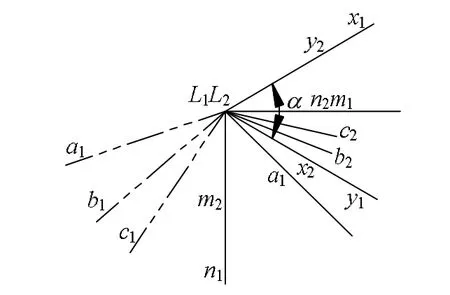
图2 二线束成椭圆形对合
与二射影线束不同的是,二射影对应面束存在两对对应合同线束。如图3所示,如果我们把共底成椭圆形对合的二面束其中之一l1(或l2)沿某一主平面移动,其对应平面的交线形成椭圆柱面,垂直于底的椭圆截面长短轴比与二面束的α角是相关的。显然,该椭圆柱面可以得到两个圆截面Rα和Sα。在Rα和Sα上,存在两对对应合同线束。为了叙述方便,我们可以称存在合同对应线束的平面为“圆面场”。两个圆面场R、S与面束底l1l2的夹角θ=arcsin(tgα/2)。
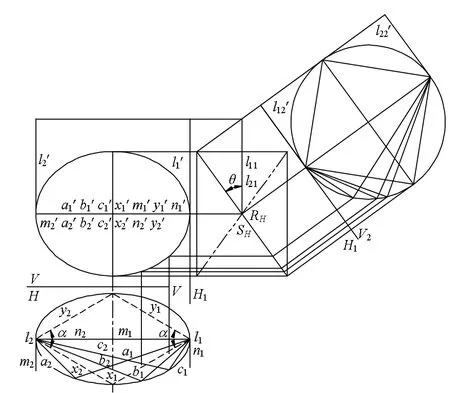
图3 二射影面束被平面R、S截切得到合同线束
2 二射影对应面束形成的锥面和单叶双曲面
如图 4所示,在l2上任取一点作圆面场R的垂线OO,让面束l2绕OO轴旋转180°,得到面束l3,l1l3二面束对应平面交线形成回转(可称圆形)单叶双曲面。显然,在圆面场R上,如果移动二合同线束共底后,成正交对合。
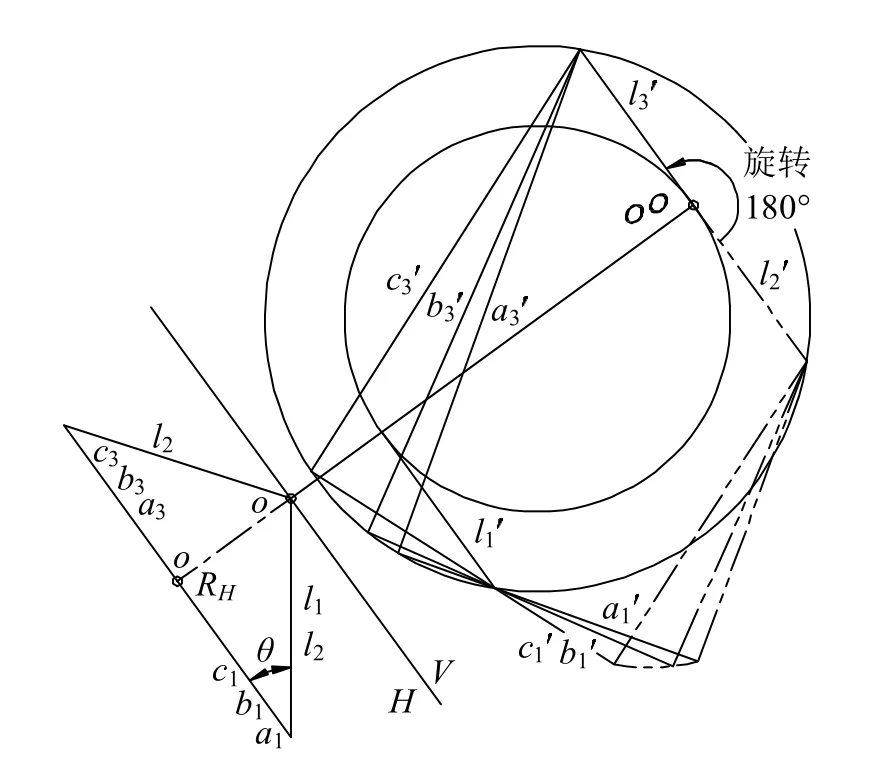
图4 L2绕OO旋转180°形成回转单叶双曲面
如图5所示,固定圆面场R不动,让l3面束平移到l4位置,这时l4与l1面束底相交,l1l4二面束对应平面交线形成圆锥面。此时圆面场上合同线束移动共底后仍然有正交对合现象。
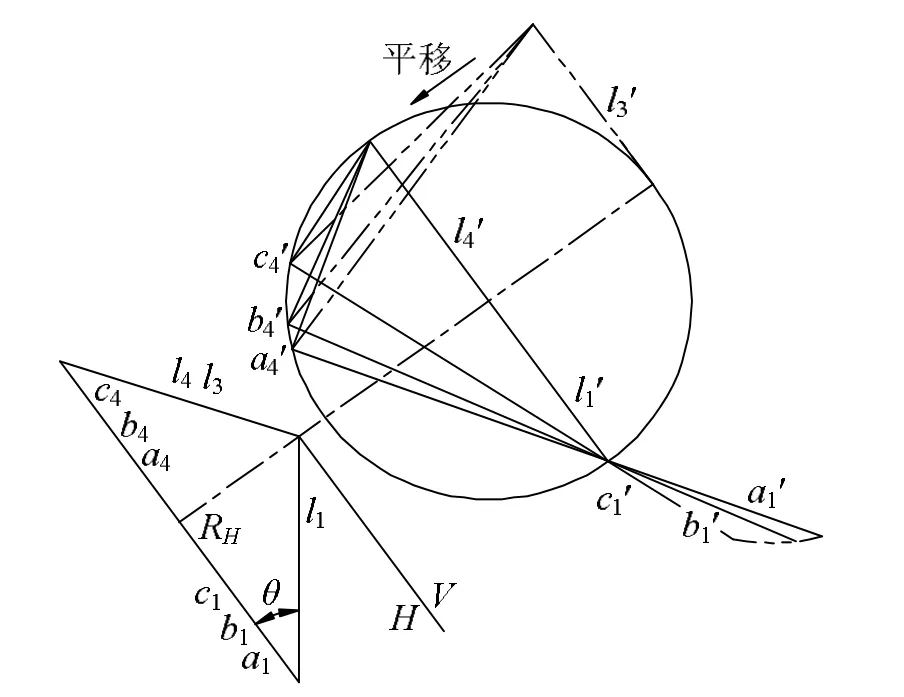
图5 L3平移与L1相交形成圆锥面
如图6所示,如果让图2中的l2面束绕OO轴旋转任意角度(锐角或钝角,90°情况另外讨论),得到面束l5,l1l5二面束对应平面交线形成正椭圆形(轴线O0O0与圆平面斜交)单叶双曲面。
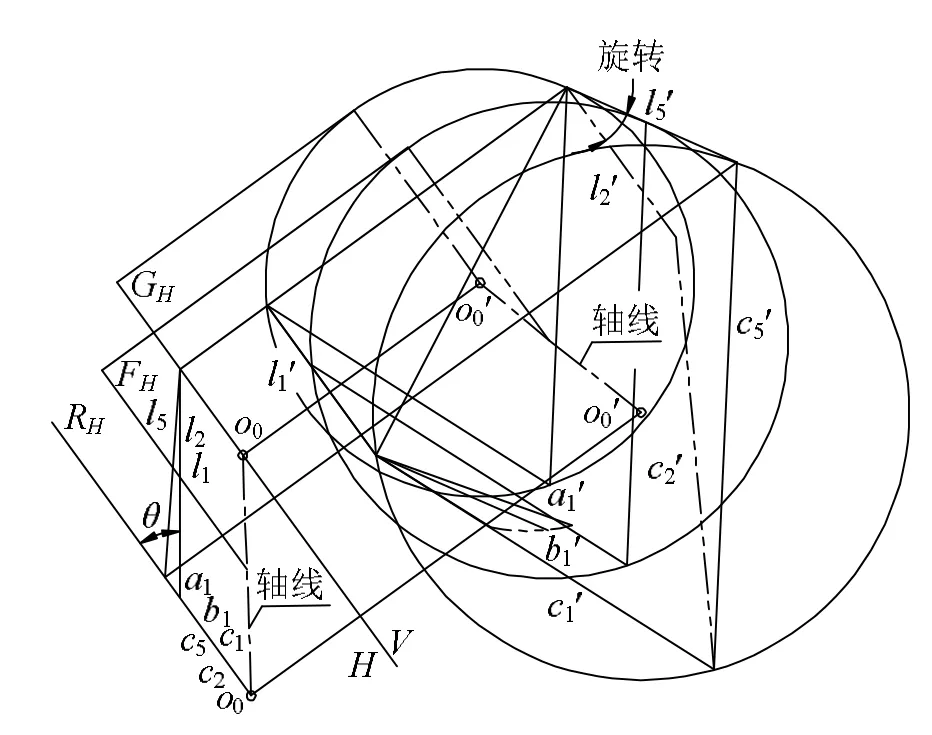
图6 L2绕OO旋转形成正椭圆形单叶双曲面
如图7所示,固定圆面场R不动,让l5面束平移到l6位置,这时l6与l1面束底相交,l1l6二面束对应平面交线形成正椭圆形(轴线O0O0与圆面场斜交)锥面。显然,这时轴线O0O0与二面束底l1l6夹角,和正椭圆形单叶双曲面中O0O0与l1l6的夹角相同,这种情况说明了锥面与单叶双曲面,在由二射影面束形成的过程中,有一种“孪生”现象。
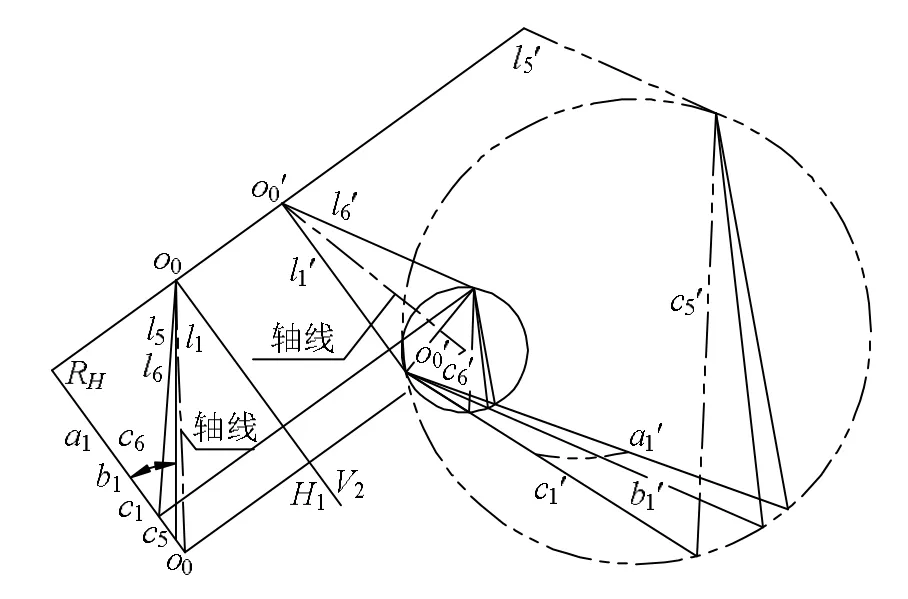
图7 L5平移与L1相交形成正椭圆锥面
空间的任意二射影对应面束,用某一平面P截切,得到截交线类型,取决于这时二射影线束存在的对应平行线数量[1]。显然,这时平移某一面束位置并不改变截交线的类型,这就是为什么单叶双曲面上,除了椭圆、双曲线,还有抛物线型截交线的原因[5]。
由于同向二合同线束对应直线交点形成圆,因此,只有二射影对应面束圆面场共面,且合同线束同向时,二次曲面具有圆截口。
斜椭圆锥面无轴线,此时生成斜椭圆锥面的二射影对应面束的圆面场不共面,因此无圆截口。与其相对应的斜椭圆形单叶双曲面同样。
3 二射影对应面束形成正斜两种形式的双曲抛物面
图8表示了T1αT2α上二射影对应线束的合同点列透视作图法,如果我们需要设计二射影面束l1l2,使其底与T1αT2α垂直,用计算机自动生成具有特定α角的二射影面束是可能的。这时若l1l2平行,形成虚柱面。l1l2相交,形成虚锥面。
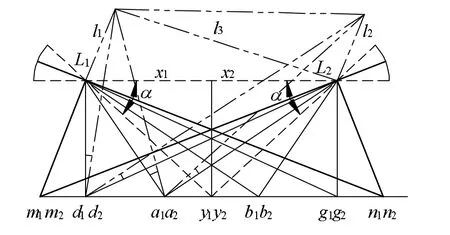
图8 合同点列法形成二射影线束
如图9所示,二射影面束底l1l2交叉,且有一对对应平行平面X1α(l1,x1)X2α(l2,x2) ,这时用任一平面P截切,不可能出现椭圆形对应线束(二线束无对应平行线),因此无椭圆截交线。所以,这时二面束形成的曲面应该是双曲抛物面。X1α(或X2α)是该双曲抛物面的导平面方向,两个面束底l1l2方向,就是其双曲线截交线的两个渐近线方向。
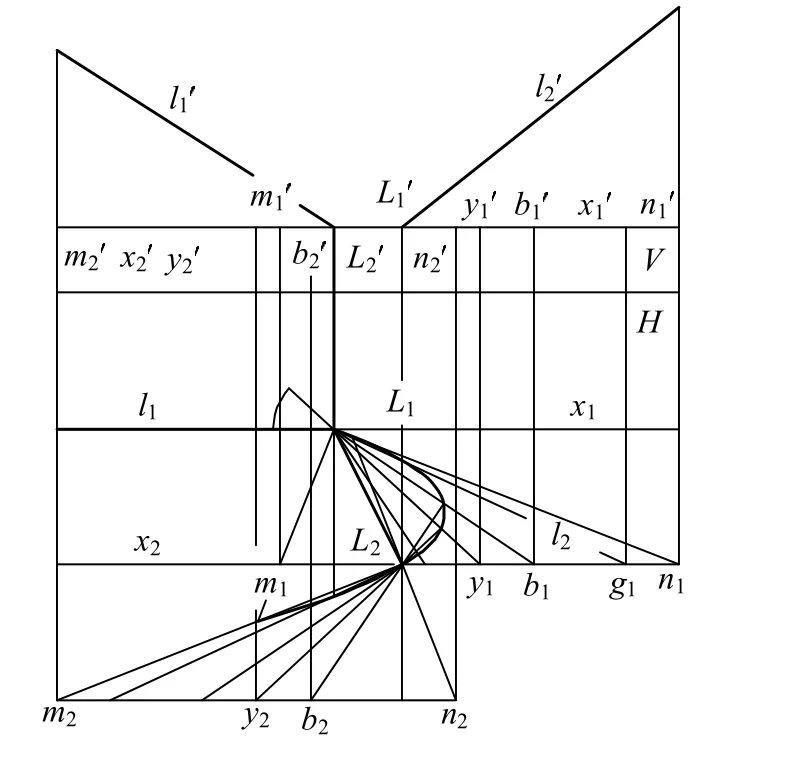
图9 二面束形成斜双曲抛物面
双曲抛物面可细分为两种形式,一种是二面束底l1l2公垂线L1L2垂直于X1α(或X2α),称为正双曲抛物面,如图 10所示。另一种是二面束底l1l2公垂线L1L2不垂直于X1α(或X2α),称为斜双曲抛物面,如图9所示。这和二合同对应点列、二仿射对应点列形成两种类型双曲抛物面并不矛盾[3]。
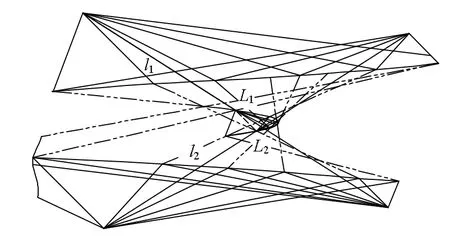
图10 正双曲抛物面斜二轴测图
4 二射影对应面束形成各种二次曲面简表
二射影对应面束底l1l2的相对位置,二射影面束存在对应平行平面的数量等因素对二次曲面的影响可以由表1来说明。
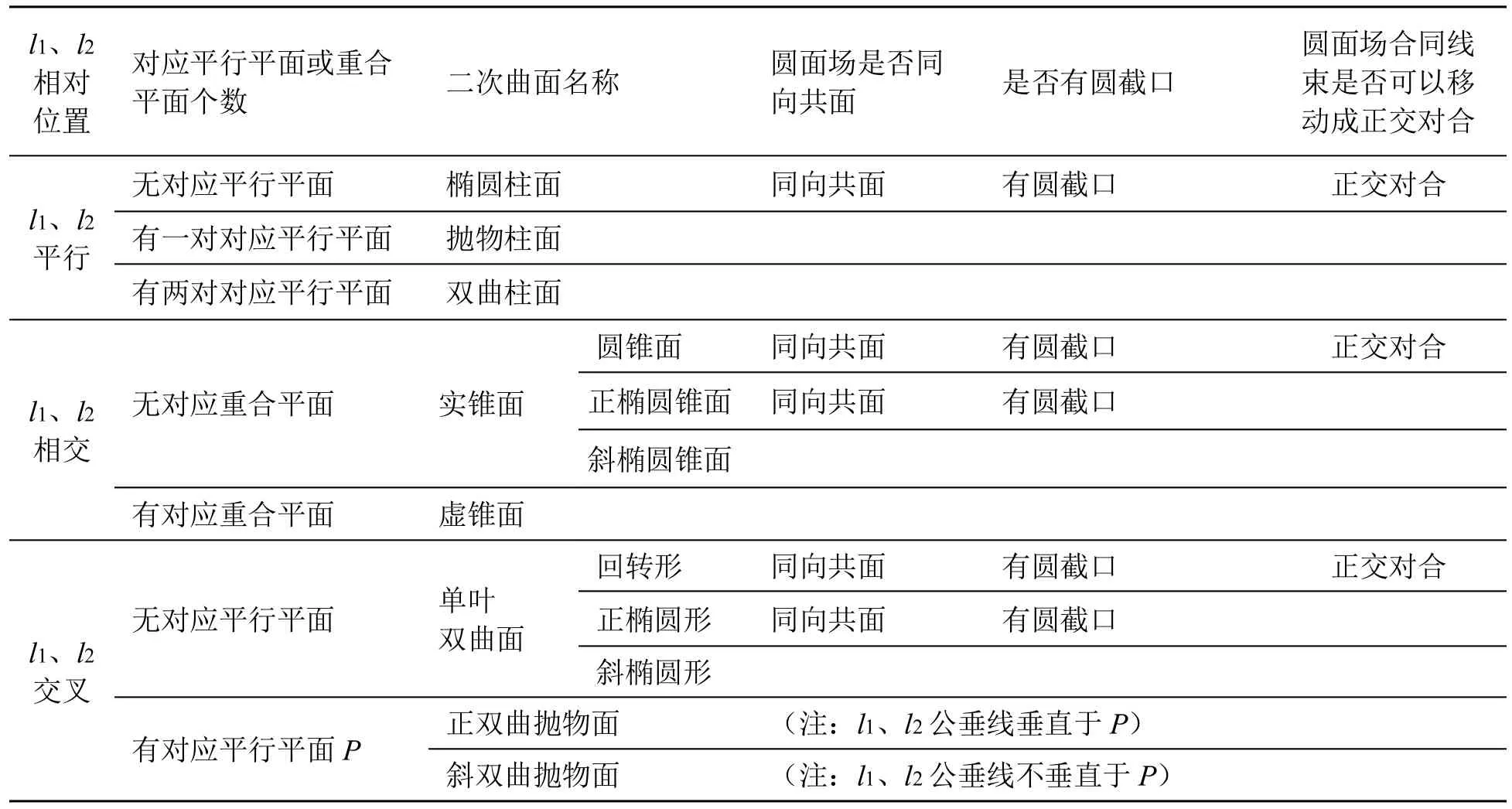
表1 射影面束形成二次曲面简表
说明:关于二平行面束形成的虚柱面可参照二射影线束的退化情况[1]。实际上,二射影面束的底也有“固对固”、“固对非”和“非对非”型,且它们的退化情况种类繁多。
5 结 束 语
通过上述讨论,我们可以尝试用计算机绘制一对对应射影面束,并让其作为最小运动单元,来生成各种柱面、锥面、单叶双曲面和双曲抛物面等。如果要生成带有圆截口的二次曲面,必须让存在合同线束的截平面同向共面。由于一对对应射影面束与另一对“大小”是不同的,这种度量性怎样影响二次曲面的形状还需进一步研究。
[1]刘阜平, 丁 勇. 射影线束形成二阶曲线及其退化形式[J]. 图学学报, 2012, 33(4): 24-28.
[2]大连理工大学工程画教研室编·画法几何学[M]. 北京: 高等教育出版社, 1992: 102.
[3]刘阜平, 丁 勇. 空间二仿射对应点列形成的双曲抛物面[J]. 工程图学学报, 2011, 32(6): 1-4.
[4]南开大学数学系《空间解析几何引论》编写组编. 空间解析几何引论[M]. 北京: 人民教育出版社, 1978:154-160.
[5]刘阜平, 丁 勇. 空间二射影对应点列形成的单叶双曲面[J]. 图学学报, 2012, 33(5): 28-31.
