二维图形最狭长包络矩形的求解原理及方法

周 敏， 郑国磊， 陈树林

（1. 北京航空航天大学机械工程及自动化学院，北京 100191；2. 沈阳飞机工业（集团）有限公司，辽宁 沈阳 110034）

二维图形最狭长包络矩形的求解原理及方法

周 敏1， 郑国磊1， 陈树林2

（1. 北京航空航天大学机械工程及自动化学院，北京 100191；2. 沈阳飞机工业（集团）有限公司，辽宁 沈阳 110034）

最狭长包络矩形是二维图形的一个潜在几何属性，可作为平面外形智能设计、板料优化排样及图像自动识别的重要依据。目前国内外尚无此课题的专门深入研究。提出了最狭长包络矩形的概念，将任意二维图形的最狭长包络矩形的求解转化为对其凸包的最狭长包络矩形的求解。明确给出了过凸包上给定4个顶点的包络矩形的包络角及长宽比求解公式，并通过分析包络角及长宽比求解公式之间的关系，证明了凸多边形至少存在一条边与其最狭长包络矩形的一条边共线。基于该定理，求解并比较与二维图形的凸包的n条边分别共线的n个包络矩形的长宽比，得到了二维图形的最狭长包络矩形。最后用实例验证了定理和求解方法的正确性和应用效率。

计算几何；最狭长包络矩形；长宽比；飞机样板设计

最狭长包络矩形是二维图形的一个潜在的固有几何属性，可作为平面外形智能设计、矩形优化排样及图像自动识别的一个重要依据。例如，在飞机样板智能化设计中，需要根据样板工作边曲线的形状，自动优化设计坐标系。而优化设计坐标系的主要途径是先找到曲线最狭长的方向，并以其作为坐标系x轴的方向，这样，可使样板所用材料最少，最轻便。如图1所示，粗实线为样板工作边，细实线为样板非工作边，非工作边平行于设计坐标系的坐标轴，A为在当前坐标系下，曲线上具有最大y值的点到非工作边的距离，A值固定；图1(a)是在未经优化的设计坐标系中设计的样板，图1(b)则是在优化后的设计坐标系中设计的样板。图1(a)中样板的面积明显大于图1(b)中样板的面积，因此，图1(b)所示样板用料更少，更轻便。那么，如何获得曲线乃至任意二维图形的最狭长方向？本文通过定义和计算二维图形的最狭长包络矩形，即可确定二维图形的最狭长方向。

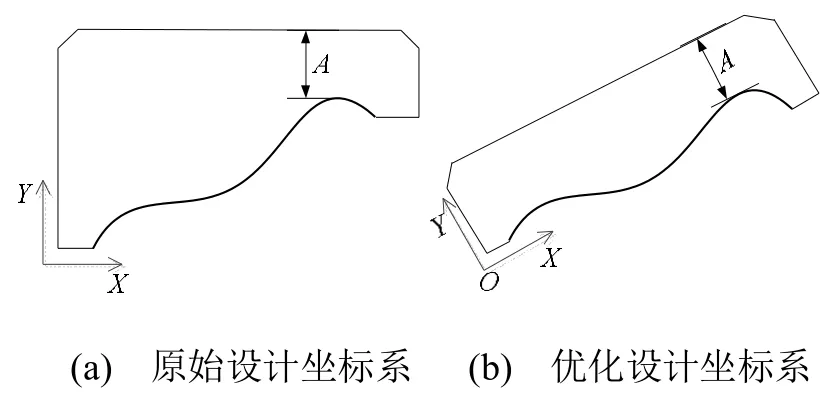
图1 不同设计坐标系下设计的样板

至今，大量研究主要围绕求解凸多边形、封闭区域图形的面积最小的包络矩形展开。Freeman和Shapira[1]证明了凸多边形的最小包络矩形必有一条边与凸多边形的一条边共线。Toussaint[2]用 Shamos[3]于 1978年在其博士论文中提出的“rotating calipers”，即旋转卡钳法求凸多边形的最小包络矩形，并将计算时间从 O(n2)缩短到O(n)（n为凸多边形的顶点个数）。Alt和Hurtaddo[4]保持凸多边形的一个顶点以及包络矩形的左下角点与坐标系原点重合，矩形两条边分别与x轴和y轴共线，旋转凸多边形，得到的包络矩形集的右上角点的轨迹，为一条由椭圆弧构成的、并以y=x为对称轴的封闭曲线；在某段椭圆弧的一个端点处，矩形具有最小面积或周长。Chaudhuri和Samal[5]用封闭区域边界点的形心作为最小包络矩形的形心，以所有边界点到矩形中心线的垂直距离之和最小作为条件来确定矩形的主轴和副轴的方向，从而求得最小包络矩形。但作者并未证明用上述方法得到的矩形就是封闭区域的最小包络矩形。黄宜军等[6]在对钣金进行排料时采用穷举法求解钣金零件的最小面积包络矩形。这种方法原理简单，但计算量大且只能获得近似值。为了提高计算效率，薛迎春等[7]利用遗传模拟退火混合算法对凸多边形的最小包络矩形进行了求解，该算法收敛速度较低且求解结果也只是近似值。

必须指出，面积最小的包络矩形并不一定是最狭长包络矩形。关于如何计算凸多边形、开曲线甚至任意二维图形的最狭长包络矩形，目前尚未见到国内外相关研究和介绍。基于智能化设计的需求以及作为对包络矩形研究的补充，本文提出并进行了二维图形的最狭长包络矩形求解原理与方法的研究。首先，将二维图形最狭长包络矩形的求解转化为对其凸包最狭长包络矩形的求解，使问题得以简化；继而，通过对经过凸包上给定4个顶点的包络矩形的包络角及长宽比的求解，以及对包络角及长宽比求解公式之间关系的分析，证明了凸多边形的最狭长包络矩形至少存在一条边与凸多边形的一条边共线；最后，基于已证明的定理，给出了二维图形的最狭长包络矩形的求解算法，并结合实例对算法进行了分析和验证。

1 最狭长包络矩形及其性质

1.1 包络角

在平面空间OXY中，G为一个二维图形，S为其离散点集，P为S的凸包，亦即凸多边形，R为P的任一包络矩形，同时也是G的包络矩形，如图2所示。P共有n个顶点，逆时针依次为v1, v2,…, vn，R的四条边依次为e1, e2, e3和e4，即有e1// e3和e2//e4，并规定分别过P上相对位置为左、下、右和上的4个顶点vl，vd，vr和vu，其中1≤l、d、r、u、≤n。此外，文中规定边与X轴正向间的夹角是指 X轴正向逆时针旋转至与边或边的延长线重合时所经过的角度，其取值范围为[0°, 180°]。图2中ω即为R中边e1与X轴正向间的夹角。这样，可给出如下定义：

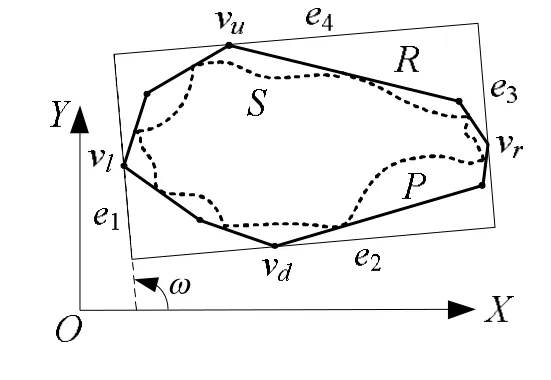
图2 二维图形的包络矩形

定义1 若顺时针（或逆时针）转动R，并使其各边始终过vl、vd、vr和vu四个顶点，且保证R为P的包络矩形，则称此转动过程为R的顺时针（或逆时针）包络转动，简称包络转动。R顺时针包络转动的极限位置称为R的包络始位，而逆时针包络转动的极限位置称为R的包络终位。

定义2 设ω为R中边e1与X轴正向间的夹角，且规定其取值范围为[0°, 180°]，则称ω为R的包络位角。

定义 3 当 R顺时针包络转动到极限位置时，称R的包络位角为R的包络始角，用ω1表示。而当R逆时针包络转动到极限位置时，称R的包络位角为 R的包络终角，用 ω2表示。令ωb=ω2-ω1，则称ωb为R的包络角。

易知，0°≤ωb≤180°，ω1≤ω≤ω2。如图 3所示，其中R1和R2分别为凸多边形P的任一个包络矩形 R顺时针和逆时针包络转动的极限位置，R为任一满足条件的包络矩形。

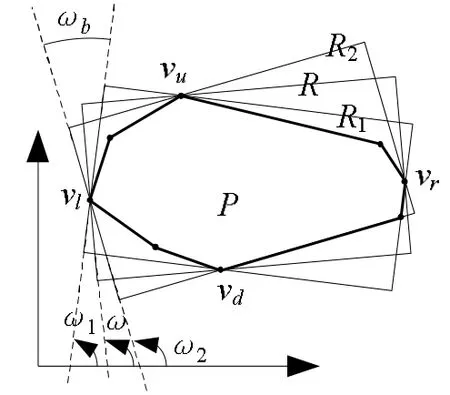
图3 包络角示意图

为求包络始角与包络终角，引入定义4。

定义4 设vp和vq为P上顶点vl的前后两个相邻顶点，vs和vt为vr的前后两个相邻顶点，如图4所示。设边与X轴夹角为与X轴夹角为同理设边与X轴夹角为与X轴夹角为若不等式

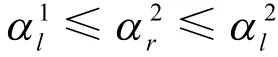
或

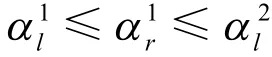
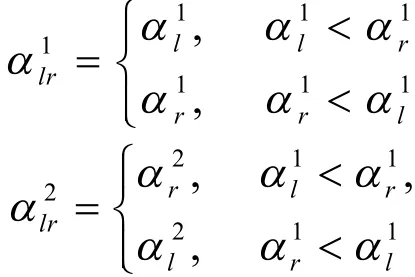
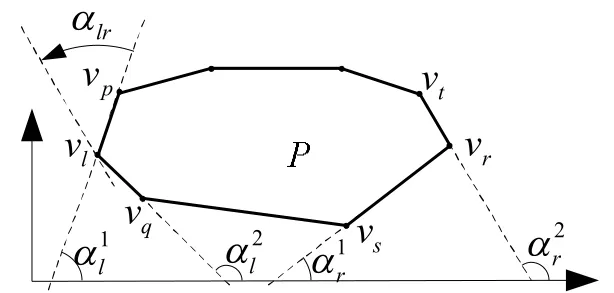
图4 包络矩形的有效转动角

引理1 在平面空间OXY中，G为一个二维图形，S为其离散点集，P为S的凸包，R为P的任一包络矩形，则R的包络始角ω1和包络终角ω2分别为：

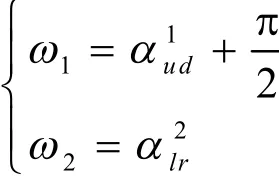
或

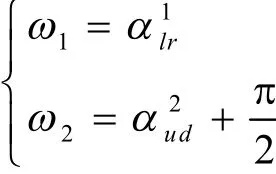
证明：由于 e1⊥ e2，因此， e2, e4逆时针旋转后应与 e1, e3平行。所以，应与有重合部分，其重合部分即为 ωb。故当不等式：

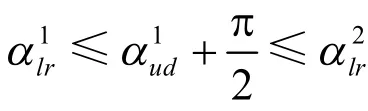
或

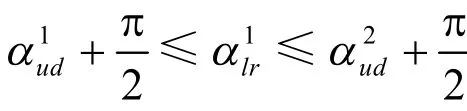
成立时，经过点 vl, vd, vr, vu，保持 e1//e3，e2//e4，e1⊥ e2且将P包络在内的矩形存在。重合部分的边界即为R的包络始角 ω1和包络终角 ω2：

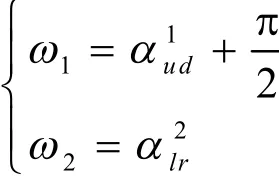
或

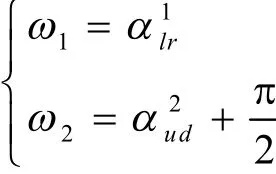
引理1得证。

引理 2 若R的包络位角为 ω1或 ω2，则 R某一条边与P的某一条边共线。

1.2 最狭长包络矩形

R为一矩形，令b和a为R的长和宽，即a≤b，称b与a之比值为R的长宽比。下文中，将长宽比的倒数用f表示，即

引理3 在G的所有包络矩形中，一定存在长宽比最大的包络矩形。

证明：设P为G的凸包， R1, R2,… ,Rm为过P上各不相同的4个顶点的m个包络矩形。其中，m为P上所有可能构成包络矩形的4个顶点的组合的个数，每一个 Ri( i = 1,2,… ,m)均可在其包络角范围内进行包络转动产生一系列过P上相同4个顶点的包络矩形，则 R1, R2,… ,Rm可表示P的所有包络矩形。 Ri在其包络转动过程中，长和宽在有限的转动范围内发生连续变化，根据实数的基本性质，连续函数在闭区间上必取到最大最小值， Ri必然在某个包络位角取得最小 fi，令其为因此，在有限的m个可数且可比较的中，及其所对应的包络矩形一定存在，亦即引理得证。

由引理3，给出如下定义和定理：

定义5 给定一个二维图形G，R为其一个包络矩形，若在G的所有包络矩形中，R的长宽比最大，则称R为G的最狭长包络矩形，表示为 ξ( G)。

定理1 设R为凸多边形P的最狭长包络矩形，则R一定存在一条边与P的某一条边共线。

证明：任意给定一个凸多边形P，如图5所示，P和 R分别由粗实线和细实线表示，线段且交线段于点 A，线段且交线段于点B，线段且交线段于点C，线段且交线段于点D，线段且交边 e3于点 E。令，，则矩形的长b、宽a分别为：

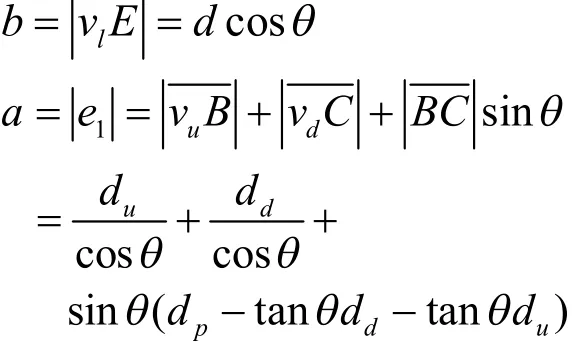
进而可得R的长宽比f为：

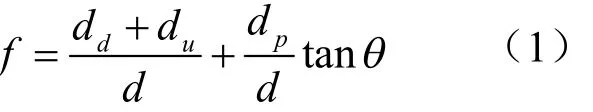
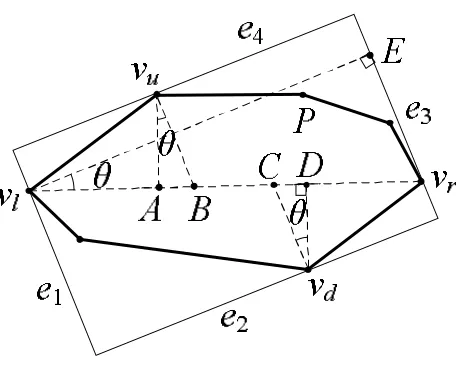
图 5 过凸包上四顶点 vl、vd、vr和 vu的包络矩形

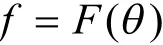
为单调递增的有界连续函数。

如图6所示，当4个顶点给定时，γ不随矩形包络转动而改变。由于 θ = ω+ γ- 180°（图6(a)）或θ =-ω- γ+ 180°（图6(b)），故θ与ω线性相关。当ω取得极限值时，θ亦取得极限值。所以当θ在 [θ1, θ2]范围内变化时，f一定在某一个θ处取得唯一一个最小值，即当包络位角ω在[ω1, ω2]范围内变化时，存在唯一一个过P上给定四顶点且长宽比最大的包络矩形。

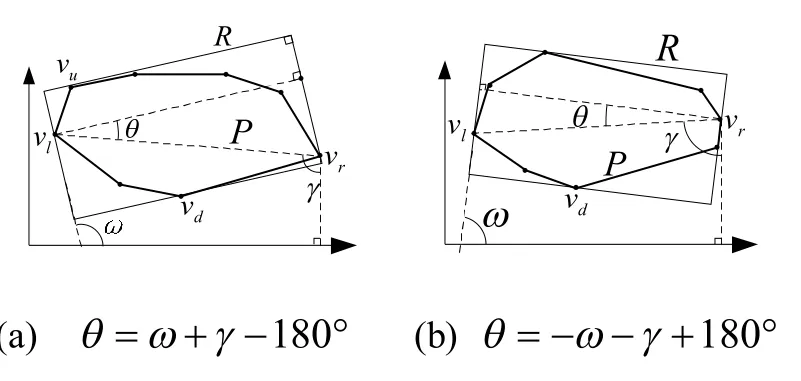
图6 θ与ω线性相关

图5中，当R逆时针包络转动时，θ角增大，f增大。当 ω = ω1时，θ = θ1最小，f最小。此时，可得到过 P上点 vl、 vd、vr和 vu且长宽比最大的包络矩形。当 ω = ω2时， θ = θ2，f最大，矩形长宽比最小。无论θ与ω正相关或负相关，f始终在 ω1或 ω2处取得最小值。

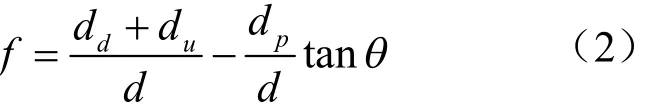
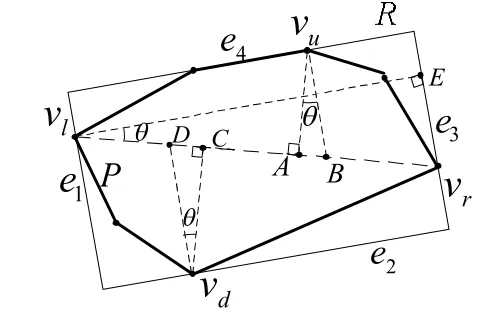
图7 当θ取得最大值时的包络矩形

当 R逆时针包络转动至使 ω = ω2时，θ最大，f最小。图 7所示为 ω = ω2时的情况。此时，矩形的一边 e4与 P的一条边重合，过 P上点vl、 vd、 vr和 vu的包络矩形长宽比最大。相反，当ω = ω1时，f最大，矩形长宽比最小。

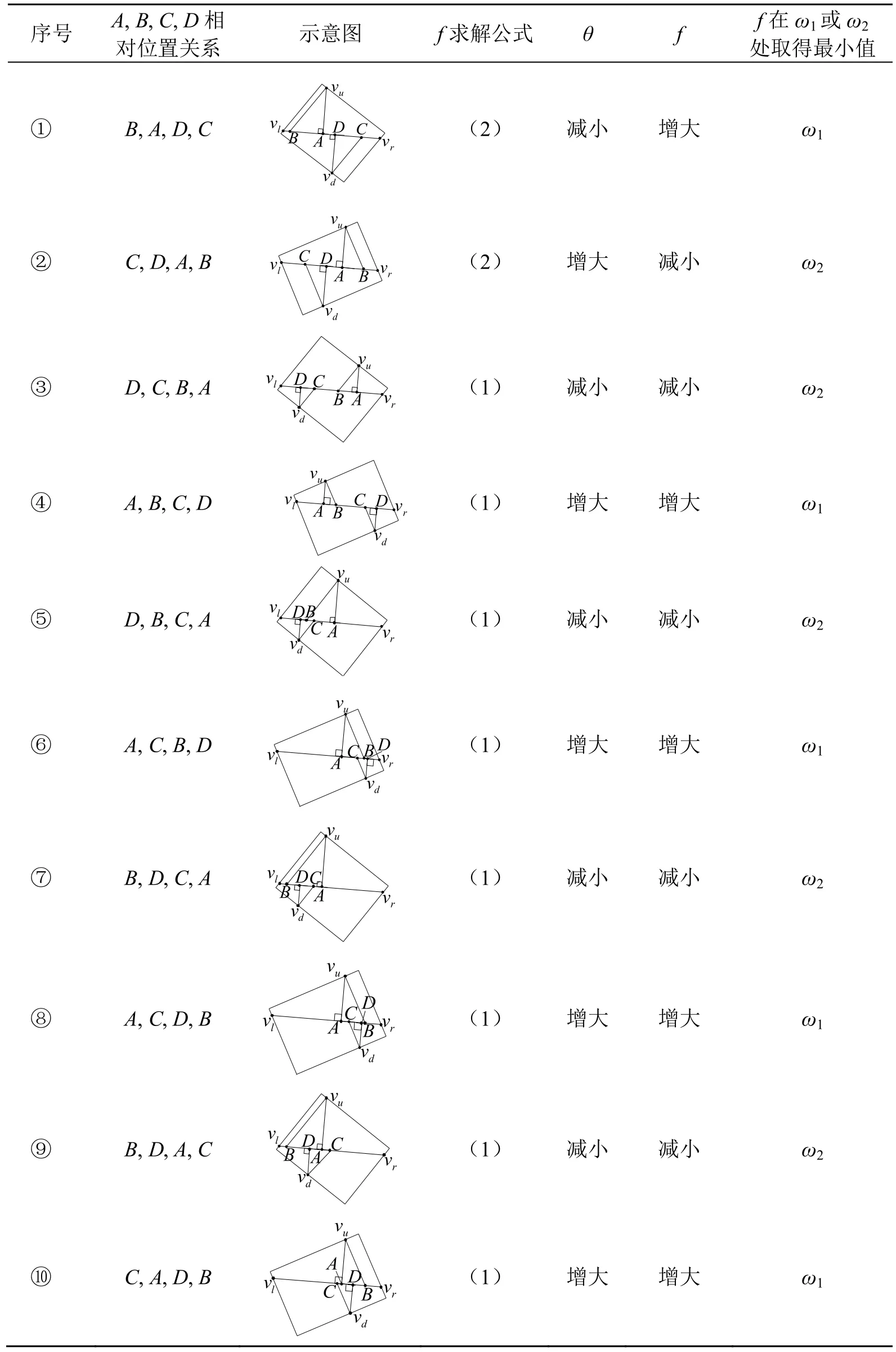
表1 矩形逆时针转动时f求解公式及其最小值

分析表1有：

2） 当矩形在满足ω1≤ω≤ω2条件的范围内转动时，A, B, C, D的相对位置关系发生变化，如由B, A, D, C（①）变为A, B, C, D（④），f的计算公式由（2）变为（1），但f仍在ω1处取得最小值；当A, B, C, D的相对位置关系继续变化时，这个结论不变。即f在何处取得最小值由A, B, C, D的初始位置确定，所以，f总是在ω1或ω2处取得最小值或最大值，而包络位角ω为ω1或ω2，矩形都有一条边与凸包的某一条边共线。由此，定理1得证。

由定理1的证明过程，同时可得出定理2：

定理2 凸多边形的长宽比最小的包络矩形一定存在一条边与凸多边形的某一条边共线。

2 计算方法及其实现

2.1 计算方法

根据定理1，二维图形G的 ()Gξ 的求解过程为：首先，将G离散为平面点集S；其次，用格雷厄姆方法[8]求解S的凸包即凸多边形P；然后，求P的n个包络矩形，并使每个包络矩形分别过P的一条边；最后，比较这n个矩形的f，f最小的包络矩形即为所求。算法流程如图8所示，其中：

Step 1 输入任意二维图形G。

Step 2 判断G的类型，如果G完全由曲线或圆弧构成，则按所需精度t进行离散，得到平面点集S；如果G包含直线段，则提取直线段端点加入点集S。

Step 3 用格雷厄姆法求点集S的凸包，得到具有n个顶点vi(xi, yi)(i=1, 2,…, n)的凸多边形P。

Step 5 对坐标系XOY作平移和旋转，使原点O与点vk重合，令新的原点为Ok，X轴的正向指向点得到坐标系对P的所有顶点作如下坐标变换：

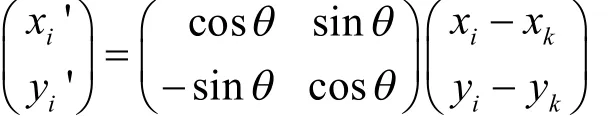
其中：

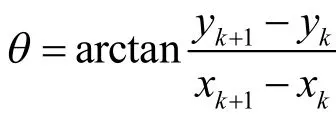
得到vi(xi, yi)(i=1, 2,…, n)在坐标系XOkY中的位置vi'(xi',yi')(i = 1,2,...,n)。

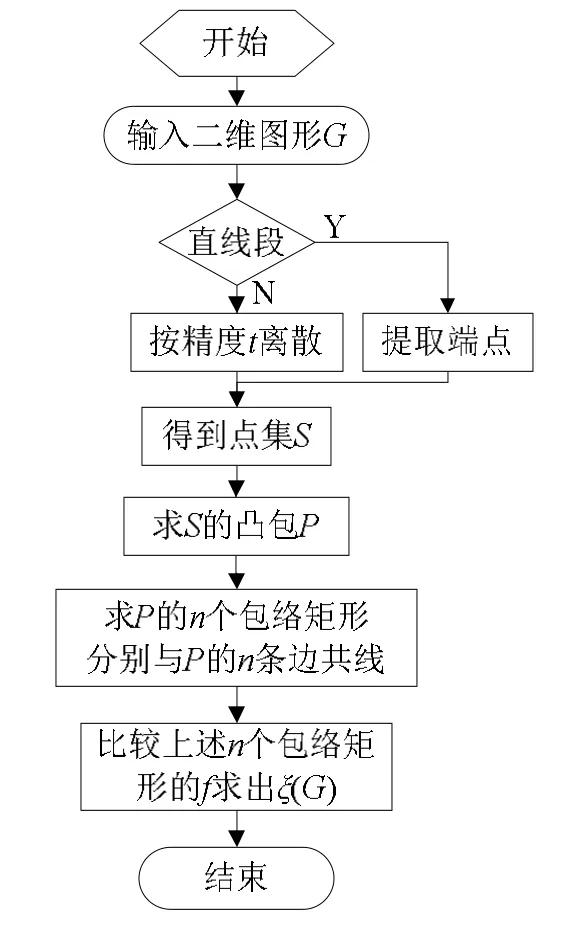
Step 6 求坐标系XOkY中，具有最大x值、最小x值和最大y值的顶点，设它们分别为vr( xr',yr')、 vl( xl',yl')和 vu( xu',yu')，则 P( S)的包络矩形的4个顶点坐标分别为(xl',0)、(xl',yu')、(xr',yu')和(xr',0)，最小 f 即为：

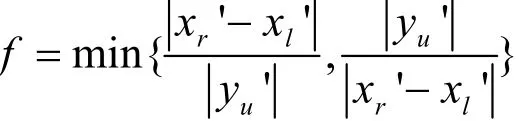
Step 7 令k=k+1，重复步骤5和6直到k=n。当k=n时，令k+1=1。比较n个矩形的n)，即可求出ξ(G)的 f 及其对应的4个顶点。

该算法时间复杂度为O(n2)。其中，n个包络矩形的求解可采用旋转卡钳法，则算法时间复杂度可降为O(n)。但本文所采用的坐标变换法简单易操作，且在满足工程需求的前提下，两种算法的计算时间并无差异。

2.2 实现及分析验证

为验证本文所提出方法的正确性，先后计算和测试了若干不同二维图形的最狭长包络矩形，其中包括4个具有代表性的图形和两个飞机壁板轮廓图。利用上述方法，分别计算了这些图形的凸包和ξ(G)，如图9至14所示。与此同时，还运用文献[6]中所述穷举法对上述实例计算ξ(G)及其对应的最小f和面积。如文献[6]所述，设矩形的对称轴共旋转90°，每旋转Δθ作一个新的包络矩形并求其f及面积。本文中分别取Δθ=1°和Δθ=1′进行计算比较。实验结果如表2所示。

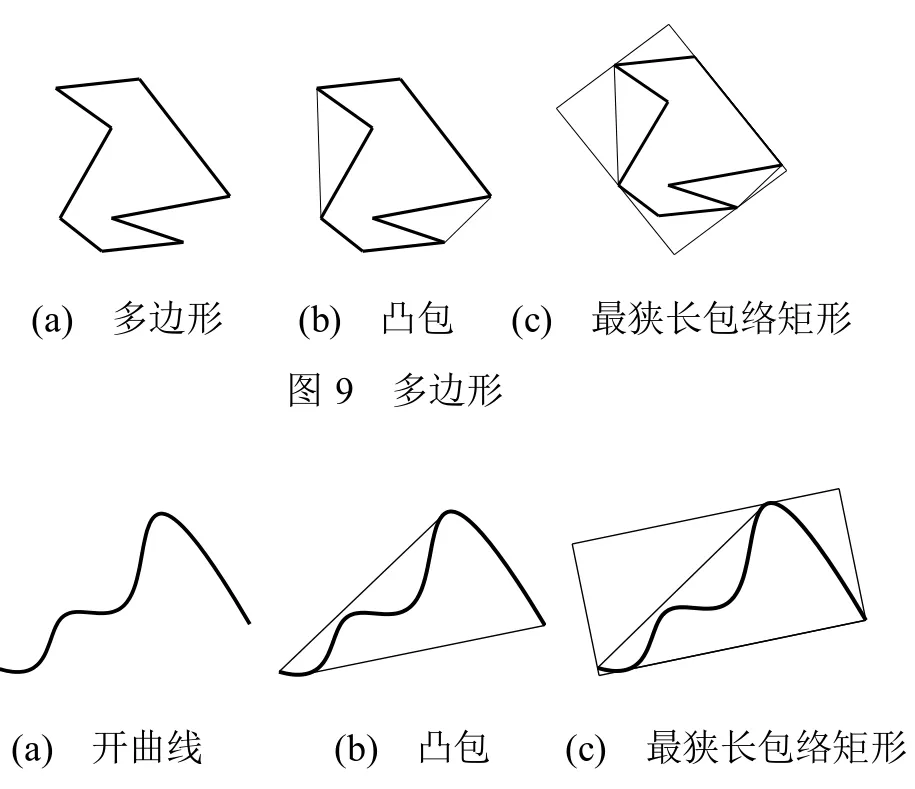
图 11 开曲线

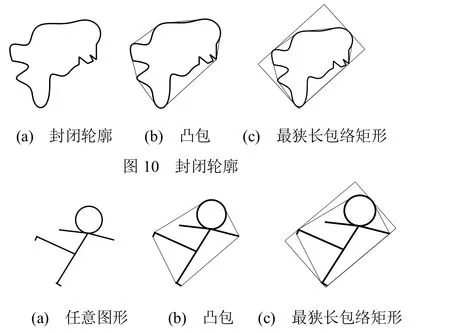
图 12 任意图形

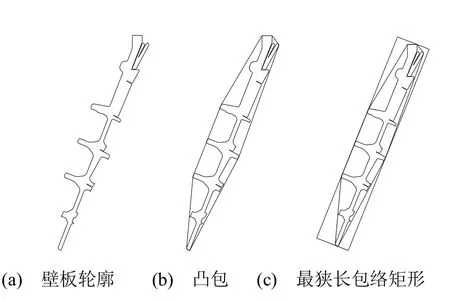
图13 飞机壁板轮廓1

图14 飞机壁板轮廓2

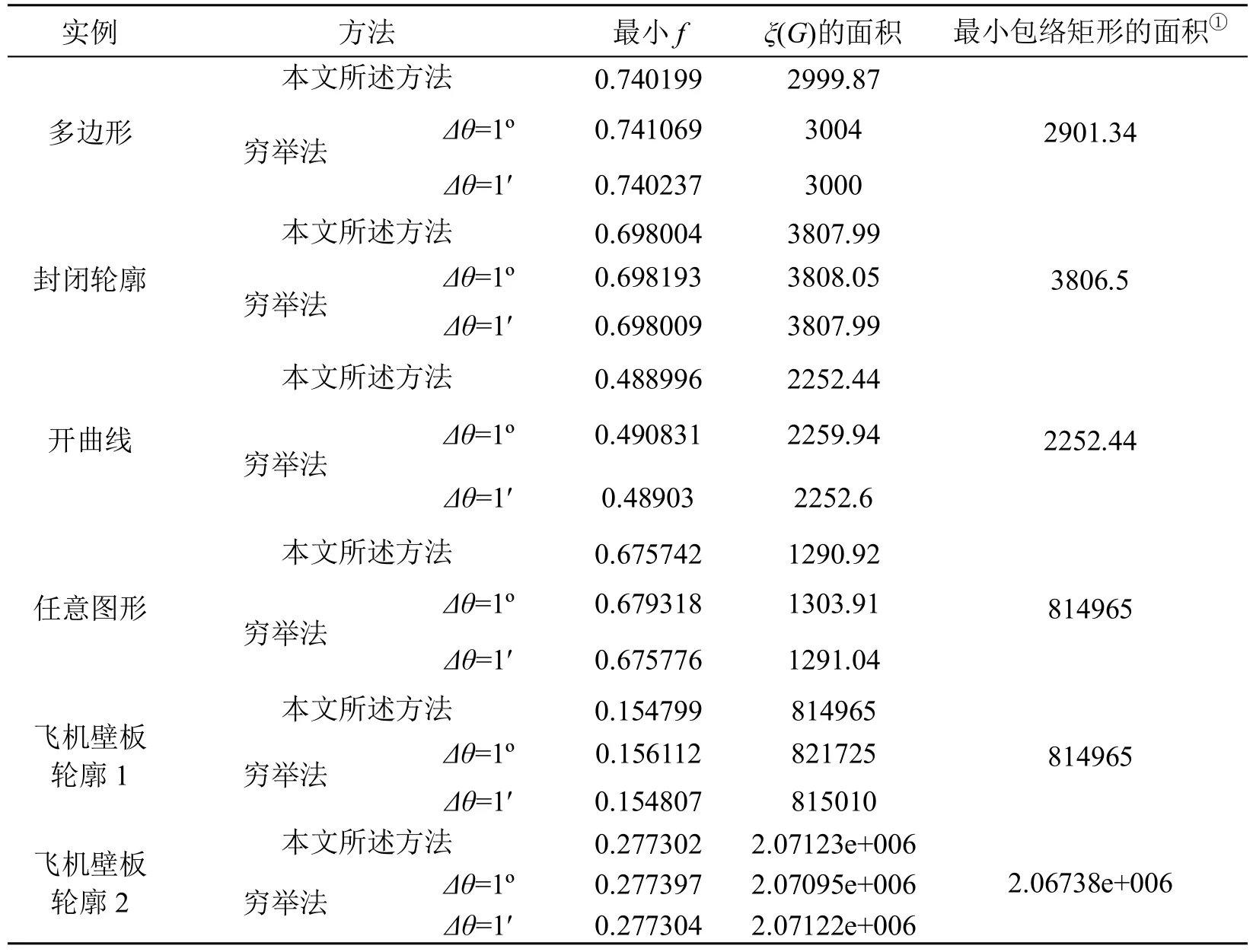
表2 本文所述方法与穷举法求ξ(G)极其f的对比 面积单位mm2

分析表2可知：

1） 当Δθ=1°和Δθ=1′时，穷举法求得的ξ(G)的最小f始终大于本文所提出方法求得的最小f。在忽略用二维图形的离散点集近似表示二维图形所产生的误差的前提下，本文所提出方法是完全精确的；而在相同条件下，穷举法只能获得近似值。

2） 当Δθ=1′时，穷举法求得的最小f比Δθ=1°时求得的值更接近本文所提出方法求得的最小f，但Δθ=1′时需要计算5400次，每次需要求四个最值，即最大x值、最小x值、最大y值和最小y值；而本文只需计算n次（n为图形凸包的边数），每次只需计算 3个最值，而两种方法每次计算每个值的时间是相等的。所以，当满足条件（Δθ单位为分）时，本文所提出方法始终比穷举法快，工程实际需求满足该条件。

3） 当包络矩形为最狭长包络矩形时，矩形的面积非常接近凸包的最小包络矩形的面积，甚至可能等于最小包络矩形的面积，这说明凸包的最狭长包络矩形与最小包络矩形不总是一致的。

综合上述对比分析，本文提出的求解方法是准确和高效的。

3 结 论

本文首次提出了包络角和最狭长包络矩形等概念，探讨了最狭长包络矩形的内在性质，并在此基础上给出了任意二维图形的最狭长包络矩形的求解方法。通过分析过凸包上给定四点的包络矩形的包络角与长宽比求解公式之间的关系，证明了凸多边形的最狭长包络矩形的某一条边一定与凸多边形的某一条边共线。基于该定理，构建了任意二维图形最狭长包络矩形及其长宽比的求解方法，此方法的核心思想是将任意二维图形最狭长包络矩形的求解转化为对其凸包的最狭长包络矩形的求解，从而大大简化了最狭长包络矩形的计算过程。最后，选用了若干典型二维图形作为实例，对本文所提方法进行计算和测试，验证了该方法的正确性和有效性。对于最狭长包络矩形的深层性质，如最狭长包络矩形个数的计算式等，还有待更进一步的深入探究。此外，如何将二维图形最狭长包络矩形的探索思路拓展到三维形体，也是下一步的研究重点。

[1] Freeman H, Shapira R. Determining the minimum-area encasing rectangle for an arbitrary closed curve [J]. Commun. Acm, 1975, 18: 409-413.

[2] Toussaint G. solving geometric problems with the rotating calipers [C]//Proceedings of IEEE Mediferranean Electrotechnical Conference (MELECON'83), 1983: A10.02/1-4.

[3] Shamos M I. Computational geometry [D]. Ph.D. thesis, Yale University, 1978.

[4] Alt H, Hurtado F. Packing convex polygons into rectangular boxes [J]. Discrete and Computational Geometry, 2001: 67-80.

[5] D. Chaudhuri A S. A simple method for fitting of bounding rectangle to closed regions [J]. Pattern Recognition, 2007, 40: 1981-1989.

[6] Huang Yijun, Shi Deheng, Xu Qifu. A better nesting method for sheet metal CAD [J]. Journal of Computer Aided Design and Computer Graphics, 2000, 12(5): 380-383黄宜军, 施德恒, 许启富. 钣金CAD中一个较优的排料算法[J]. 计算机辅助设计与图形学学报, 2000, 12(5): 380-383.

[7] Xue Yingchun, Xu Wenbo, Sun Jun. Rectanglepacking optimization utilizing hybrid genetic algorithms [J]. Computer Engineering and Design, 2007, 28(22): 5457-5460.薛迎春，须文波, 孙 俊. 基于遗传模拟退火混合算法的矩形包络求解[J]. 计算机科学与工程, 2007, 28(22): 5457-5460.

[8] Zhou Peide. Computational geometry—algorithm design and analysis [M]. 2nded. Beijing: Tsinghua University Press, 2005: 101-102.周培德. 计算几何——算法设计与分析(第2版). [M].北京: 清华大学出版社, 2005: 101-102.

The Solution to Determine the Bounding Rectangle with Maximum Aspect Ratio for 2D Graphics

Zhou Min1, Zheng Guolei1, Chen Shulin2
( 1. School of Mechanical Engineering and Automation, Beihang University, Beijng 100191, China; 2. Shenyang Aircraft Industry(Group) Corporation Ltd, Shenyang Liaoning 110034, China )

The bounding rectangle with maximum aspect ratio is a potential property of 2D graphics. This plays important roles in applications including the intelligent design of plane geometry, certain packing and optimum layout problems, as well as pattern recognition. However, no previous research is known for the problem. In this paper, a solution based on the convex hull of the given graphics is proposed to determine it. By analyzing the formulae for the maximum aspect ratio and the rotation range of the rectangle on which four given vertexes of the polygon are, one significant theorem is introduced and proved to show that one side of the maximum-aspect-ratio enclosing rectangle must be collinear with an edge of the enclosed polygon. According to this theorem, we determine the target rectangle by computing and then comparing the aspect ratios of n bounding rectangles which respectively have a side being collinear with different edge of the graphics’ convex hull with n edges. The experimental results are showed to prove that the solution is both accurate and efficient.

computational geometry; bounding rectangle; aspect ratio; aircraft template design

TP 391.7

A

2095-302X (2013)04-0046-08

2012-10-11；定稿日期：2012-11-19

周 敏（1985-），女，四川崇州人，博士研究生，主要研究方向为面向智能化设计制造的模型几何属性计算方法与应用。E-mail：zhoumin.buaa@139.com

郑国磊（1964-），男，福建莆田人，教授，博士生导师，主要研究方向为CAD/CAM，夹具智能化设计和数字化装配。E-mail：zhengguolei@buaa.edu.cn陈树林（1984-），男，江西余江人，博士，主要研究方向为CAD/CAM/NC。Email: csl_buaa@139com