NURBS曲线的收敛性分析

石 茂

（陕西师范大学数学与信息科学学院，陕西 西安 710062）

非均匀有理B-样条参数曲线(NURBS)是计算机辅助几何设计和计算机图形学的主要数学工具之一。它不仅可以精确表示二次曲线，还可以通过权因子ωi调控曲线的形状。给定节点向量u={u0,u1,…,un}，权因子向量ω= { 1,ω1, … ,ωn-1,1}及其控制顶点pi,0≤i≤n，p次NURBS曲线可递归定义为[1]

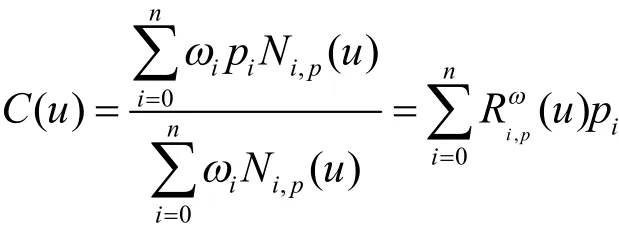
其中Ni,p(u)是p次B样条基函数，且有如下递归定义：

其中(u)可以看成是关于权因子ωi的函数族。到目前为止，虽然对权因子ωi→+∞时，NURBS参数曲线的收敛性有了一些重要的结果，但是，依旧没有一个比较权威的结论。Pigel在文献[2, 3]中指出有理参数曲线的极限为 3个点，但是，在文献[2]中又给出其几何意义为两条线段ipp0和nipp。虽然这一结论令人困惑，但已被几何设计和计算机图形学界广为接受[4,5]，并被推广到了NURBS曲线上[6-9]。在文献[10]中，虽然指出有理参数曲线具有逐点收敛和非一致收敛性;但是在一般情况下，逐点收敛并不能推出L1收敛[11]，而L1收敛则能很好的解释收敛曲线为线段p0pi和pipn这一问题。因此，对有理参数曲线的L1收敛的研究是很有必要的。本文在文献[12]的基础上给出 NURBS参数曲线关于某一权因子ωi→+∞时的收敛性分析。全文用到的逐点收敛，一致收敛，L1收敛和拓扑同胚等相关概念。读者可以查阅本文给出的相关参考文献[13-15]。不失一般性，本文仅仅考虑u∈ [ui,ui+1]区间上的一条NURBS曲线。

1 非一致收敛

引理1 有理基函数是关于权因子iω逐点收敛的，而不是一致收敛的。

证明：由

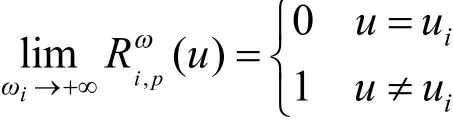
可得命题成立。

引理2 给定2个固定常数c,d∈R，u＜c＜d＜u。那么(u)在u∈ [c,d]上是关

ii+1于权因子ωi一致收敛的，且(u)⇒1，其中“⇒”代表“一致收敛”。

证明：对∀ε＞0，由

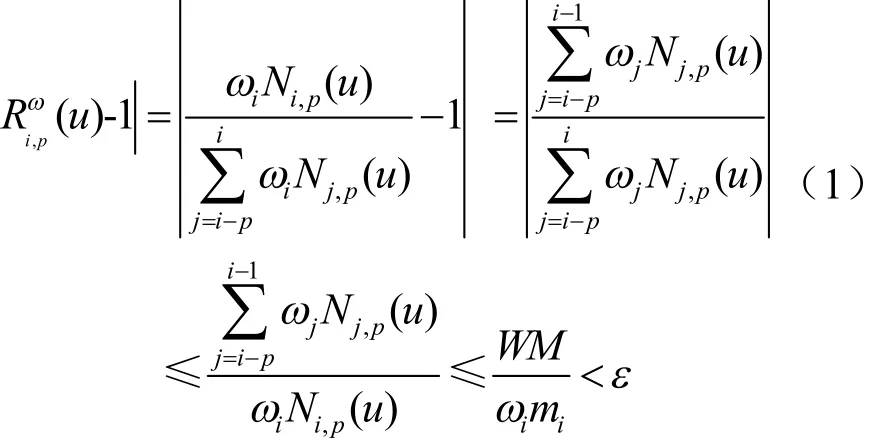
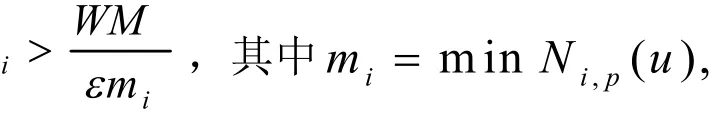
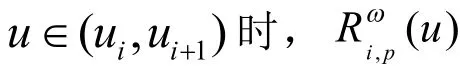
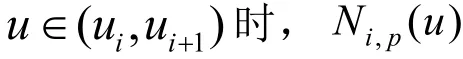
定理1 对p次NURBS曲线，当ωi→+∞时，其在u∈ [ui,ui+1]是逐点而非一致收敛的。

定理2 给定两数c,d∈R,且ui＜c＜d＜ui+1，对 ∀u∈ [c,d]，当ωi→+∞ 时，NURBS曲线是一致收敛的。

2 L1收敛

对NURBS参数曲线的L1收敛分析要涉及到积分计算，那将是一个非常繁杂的过程，以至于可能得不到解析表达式。在本文中，将应用同胚这一概念对此问题进行分析。这是因为，在拓扑分析中，如果两个空间是同胚的，那么它们具有相同的几何性质，所以这两个空间也可以看成是相同的[14]。

定理3[15]仿射变换是同胚变换，即仿射变换后的曲线和源曲线是同胚的。

通过定理3，可以将被积区域简化为由参数曲线和x轴形成的单连通区。

定理4[16]任何平面单连通闭合曲线同胚于圆周。

定理4为庞加莱猜想n=2的情况。因此，如果我们要讨论在区间u∈ [ui,ui+1]上的任意一条p次NURBS曲线关于权因子ωi→+∞时的L1收敛性，那么,仅仅考虑与其同胚的特殊曲线就可以了。

定理5 当ωi→+∞时，任意一条三次有理Bézier曲线L1收敛到线段p0pi和pi p3(i=1,2)。

如图1所示。

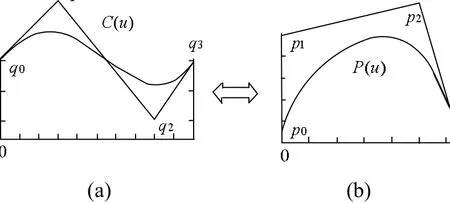
图1 平面一三次有理Bézier曲线C(u)，通过通胚变换到曲线P(u)示意图，其中q0对应p0，q1对应p1，q2对应p2，q3对应p3，权因子也依次对应

证明：由定理3和定理4，可以得到任意一条三次有理 B é z i e r参数曲线与以p0= ( 0,0),p1= ( 0,1),p2= ( 1,b),p3= (a,0)为控制顶点，其中a＞0，ω= ｛ 1,ω1= 1 ,ω2,1｝为权因子的有理三次参数曲线P(u)是同胚的（如图1所示），相应的表达式为：

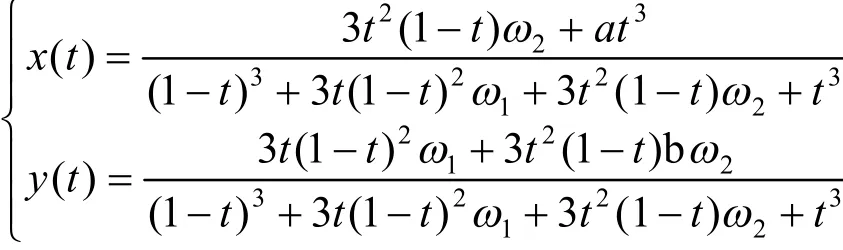
通过mathematica求解得

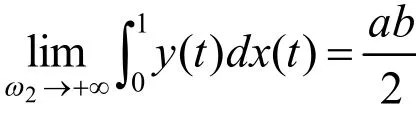
因此,说明当权因子ω2→+∞时，任意一条三次有理Bézier参数曲线收敛到线段p0p2和p2p3如图2所示。

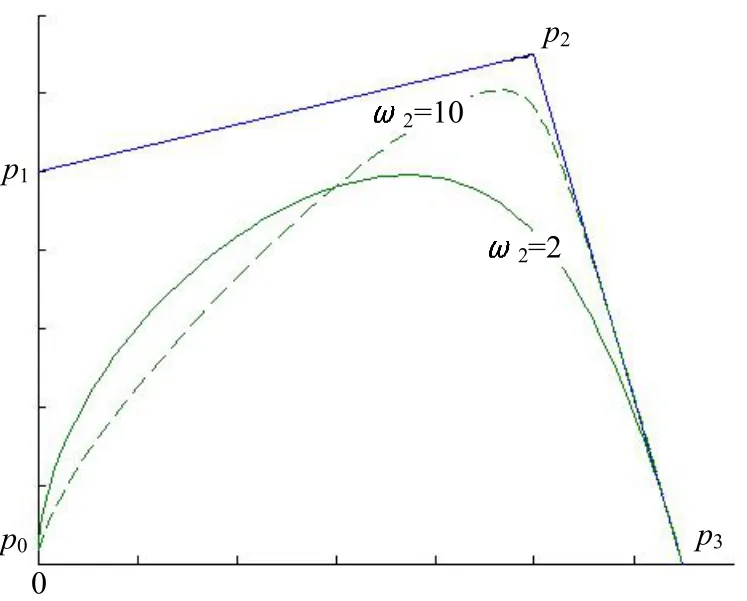
图2 当权因子→+∞ 时，三次有理Bézier曲线P(u)收敛到线段 p 0 p2和 p 2p3

类似，也可以证明当权因子ω1→+∞时，任意一条三次有理 Bézier参数曲线收敛到线段p0p1和p1p3。最终命题得证。

本方法还可以推广到对更高次有理参数曲线的关于权因子ωi→+∞时的讨论上。

4 结 论

本文讨论了 NURBS参数曲线的收敛性分析。如何求高次有理参数曲线的面积和对有理参数曲面的收敛性分析，将是我们今后研究的重点问题。

[1]Pigel L, Tiller W. The NURBS Book [M]. Springer,1997.

[2]Piegl L. A geometric investigation of the rational Bézier scheme of computer aided design [J]. Computer in Industry, 1986, 7(5): 401-410.

[3]Piegl L. letter to the editor [J]. Computer Aided Geometric Design. 1986: 79-81.

[4]王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M].北京: 高等教育出版社, 2001.

[5]施法中. 计算机辅助几何设计与非均匀有理B样条[M].北京: 高等教育出版社, 2001.

[6]孙家广, 胡事民. 计算机图形学基础教程(第 2版)[M]. 北京: 清华大学出版社, 2010.

[7]彭群生, 金小刚, 万华根, 等. 计算机图形学应用基础[M]. 北京: 科学出版社, 2009: 28.

[8]吴宗敏, 刘建平, 曹 沅等译. 金字塔算法：曲线曲面几何模型的动态编程处理[M]. 北京: 电子工业出版社, 2004.

[9]王仁宏, 李崇君, 朱春刚. 计算几何教程[M]. 北京:科学出版社, 2008.

[10]石 茂, 汪国昭, 康宝生. 二次有理 Bézier曲线的几何逼近与应用[J]. 西北大学学报, 2005, 35(4):377-378.

[11]周民强. 实变函数轮（第2版）[M]. 北京: 北京大学出版社, 2008.

[12]Shi Mao, Ye Zhenglin, Wang Guozhao et al. The convergence analysis for the rational Bézier curves [J].Journal of Information & Computational Science,2010, (7- 8): 1643-1648.

[13]Boggess A, Narcowich F J. A first course in wavelets with fourier analysis [J]. Pearson Education, Inc,2001.

[14]Choquet G. Topology [M]. Academic Press, 1966.

[15]Coxeter H S M, Greitzer S L. Geometry Revisited[C]//The Mathematical Association of America, 1967.

[16]Cao H D, Zhu X P. A complete proof of the poincaré and geometrization conjectures-application of the hamilton-perelman theory of the Ricci flow [J]. Asian Journal of Mathematics, 2006, 10(2): 165-492.