基于寻源与跟踪“FAST”主动反射面的形状调节*
2022-09-05王帮艺廖玉梅曹永林周晓琴
王帮艺,廖玉梅,曹永林,周晓琴
(贵州师范学院数学与大数据学院,贵州 贵阳 550018)
0 引言
在确认目标天体定位的前提下,利用信号接收系统(馈源舱)对平行电磁波反射产生的汇聚特征,要设定一个理想抛物面,把反射平面调节为一个工作抛物面,尽量接近理想抛物面,从而获得天体电磁波经反射面反射后的最佳接收效果,而“FAST”主动反射面刚好能满足。但其在使用时会存在较大误差,本文基于该问题建立了寻源与跟踪的模拟过程,能对 “FAST”主动反射面形状进行精准调节,解决了误差问题,得到各种目标天体的理想抛物面。
1 寻源与跟踪原理
寻源与跟踪原理如图1。寻源与跟踪的计算流程如下:
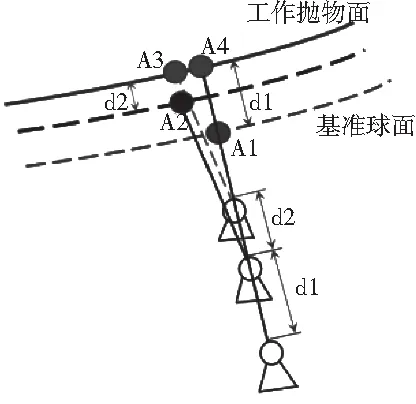
图1 寻源与跟踪原理Fig.1 Principle of source searching and tracking注:寻源过程与跟踪过程都是将反射面调节到工作抛物面的模拟过程。
第一步:先测量太阳照射方位及口径内球面索网各节点至抛物面的间距;第二步:向一定口径范围内的所有下拉索的下部施以强迫位移。但因为索网体系的整体效应,在结构达到均衡状态时,当节点移动后,同样也会有相应的切向变化,因此割向变化量也极小;第三步:多次重复第一、二步,直到主索节点与给定抛物面之间的最大间距达到一定精确度条件,拉索与下端节点的每一个位置之和就是促动器要调整的位置;第四步:如果只进行寻源,变位过程结束,如果需要进行跟踪,则返回到第一步。
2 “FAST”主动反射面模型建立
“FAST”主动反射面形状的调节。当待测天体的位置为α=0°,β=90°时,根据FAST的工作原理以及反射面板的结构,绘制被观测天体的剖面图。并且旋转抛物面每次变位后,500 m口径球面内在抛物面和球面之间变换,都会有不同的焦点,且都位于焦面上,再根据初始基准球面的空间结构及球面与旋转抛物面之间具有各向同向特征[2]旋转对称,简化问题,用二维平面问题对问题进行求解。
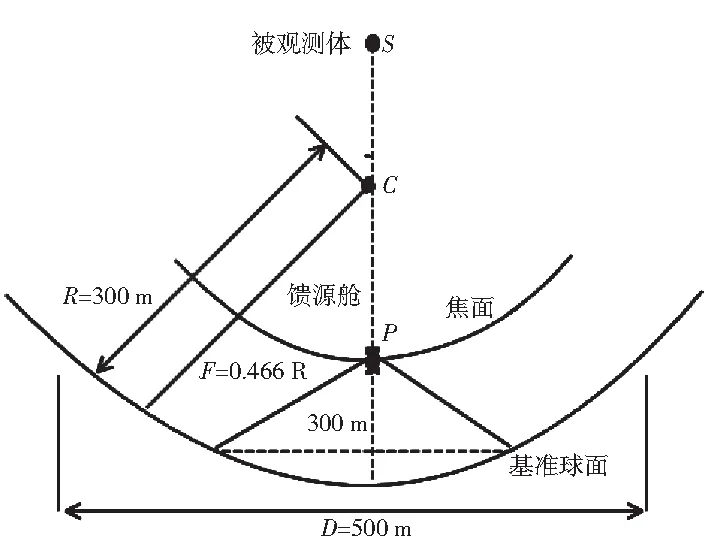
图2 “FAST”主动反射面模型Fig.2 Model of the active reflector of “FAST”
设p为旋转抛物面的焦距,R=300 m为基准球面半径,h为工作抛物面顶点与基准球面的相对位置,即抛物面顶点与球面顶点间的距离。由圆与抛物面的方程,及焦面与基准球面的半径差、抛物面的口径,计算得旋转抛物面的焦点径比q=0.466,旋转抛物面的焦距p=138.9。因为被测天体位于球面正上方,要使指定抛物面与理想抛物面贴合度最大,确定理想抛物面时要考虑基准球面与工作抛物面的相对位置大小[2]。主索节点的移动变位由推动实现器的伸缩来调节,当下拉索的尺寸不变,且工作抛物面在接近基准球面处的球心方向为正时,得到三条抛物线的表达式为:
(1)
当h=0时,工作抛物面顶点与球面顶点重合,该种情况贴合最优,不考虑。基于以上分析,从四个方面来说明工作抛物面与基准球面的贴近情况。
当基准球面与工作抛物面的径向位移最小时,取球面上主索点在x轴上的变量范围[0,150],分析步长1 m,设L径为主索节点的径向位移,LCM为M点到球心的距离[2]。
L径=R-LCM
(2)
结合h为0.6或-0.6时两抛物线方程及圆弧方程,利用Matlab进行数值分析,得到径向位移的变化图。h=0.6时,径向位移为[-1,0.6],促动器的最大伸缩量为1.6 m;h=-0.6时,径向位移为[-1,-0.6],促动器的最大伸缩量也为 1.6 m。选取径向位移最短、最大伸缩量的值最小时为最好。

图3 径向位移变换Fig.3 Radial displacement transformation
当基准球面与工作抛物面的经向弧长最小时,在经向方向,设球面顶点N,抛物线顶点A,M在二维球面圆弧上的坐标为(x0,y0),抛物线上的坐标为(x1,y1),则M到抛物线顶点的弧长为LAM,同样,设M到球面顶点N的弧长为LNM,设θ为M点到y轴的夹角,有:
(3)
结合h为0.6或-0.6两抛物线方程及圆弧方程,进行数值分析,若要考虑主索网顶点对应x值,增加其可靠性,则必须使弧长L经最小为1。
当基准球面与工作抛物面的纬向弧长最小时,考虑纬向方向上的纬向弧长[2]及其相对基准球面的纬向弧长变化的百分比。因为被测物体位于球面球心正上方,所以求出纬向弧长变化为[1.5%,37.5%]。但要确保索网的整体结构不松弛,反射面必须调整到抛物面状态时,必须使主索网受到最大内力应小于设计值,ΔL纬应尽量小,则要满足它们最大值和最小值的差最小。
(4)
当基准球面与工作抛物面的边缘径向位移最小时,因为主索网由短程线三角网格构成,每个三角网格上都有一定大小的反射面板构成,所以旋转抛物面与球面之间的过渡不是连续的,但我们要解决主索节点间的疲劳问题,则必须使它们进行光滑过渡,即把抛物面边缘节点的径向位移为0,且球面与工作抛物面相交处的曲率相等,即它们对应的函数在该点的导数值相等,得到:
(5)
由此可以解出x0、y0的值。再将x2=2py对x求导,在边缘径向位移最小的情况下,它们之间的导数差要最小。
最后对抛物面的优化,要使基准球面与工作抛物面间尽量贴合,需要满足促动器行程最小、径向位移最小、纬向位移最小、交点导数值最小。所以当q=0.466时,利用蒙特卡洛法[4]在(-0.6~0.6)随机选取h生成抛物面。基于此,建立最优模型,为权衡主动反射面的5个影响因子,为每个因子设置权重[2]。
min|H=aΔL径+bΔL经+cΔL纬+dL边-ey′|
(6)
综上,因为被测物体位于基准球面球心正上方,且-0.6≤h≤0.6,焦径比和抛物面的口径的大小已确定,综合考虑众多影响因素,得到抛物面的最优h=0.45 m,得到理想抛物面的方程。
因为需要解决理想抛物面的确定、它的位置的相关信息及促动器伸缩量,所以分步实现。首先确定理想抛物面。当α=0°,β=90°和α=36.795°,β=78.169°时,因为圆弧与抛物线都具有对称性,得到两个反射面的位置。因为仅改变天体的观测方向,所以设工作抛物面和基准抛物球面的相对距离为h1,其中焦距为 138.9 m,焦径比为 0.466,h的范围为-0.6 ~ 0.6,得到:
(7)
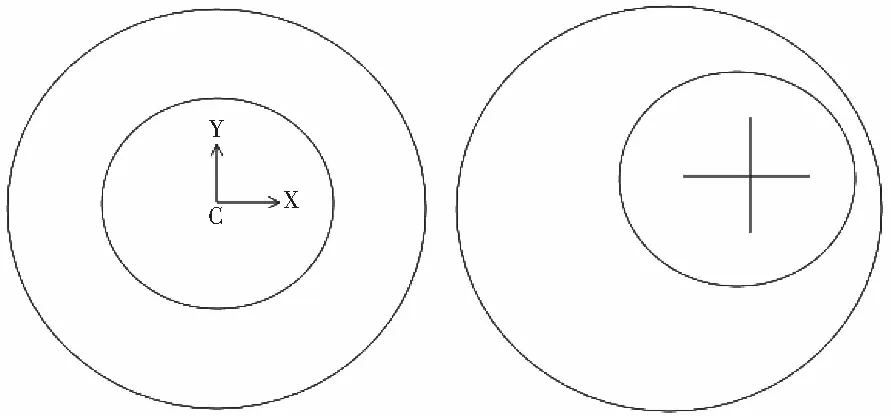
图4 调节后两个反射面的关系Fig.4 The relationship between the two reflectors after adjustment
观察、比较发现抛物面与反射面间的纬度距离在减少,但纬度环比不变,所以不考虑纬径上的变化,和它们之间的平滑过渡[5],设M1为工作抛物面的主索节点,我们引用前面的模型,考虑工作抛物面与基准球面的经向方向的位移变化,再利用优化模型,求出最优h1,确定理想抛物面。
要确定理想抛物面的顶点坐标、位置相关信息及促动器伸缩量,通过处理相关数据,得到两个相差无几的空间三维球面,即可以把促动器的伸缩量看作地面相应促动器间的距离变化处理。
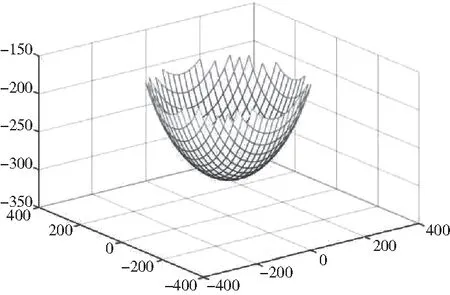
图5 部分反射面板的三维空间图Fig.5 3D space view of part of the reflector panel
寻源过程与跟踪过程都是将反射面调节到工作抛物面的移动过程,利用其原理解决问题,连接基准球面上主索节A1,与球心过理想抛物面的另一个主索节点A2,设两个主索节点对应的促动器之间的距离为x,由因为A1与A2不可能重合,交理想抛物面于A3、A4两主索节点对应的促动器的距离为x1,以此类推,得到众多xi(i=1,2,…,n),由促动器的工作原理可知,xi的值即为促动器伸缩量[5],由于抛物线与圆弧都具有对称性,取区间[0,150],将抛物线下面分割成n(n=1113)个小曲边梯形,由抛物线的对称性,则每个小曲边梯形的宽为ξ=0.135,设照射反射面上各节点到理想抛物面的距离xi,得到每个小曲边梯形的面积Si,从而得到抛物面围成的总面积S。
(8)
求出来的每个xi的值,即为促动器的伸缩量,又因为对称性可得另一侧促动器的伸缩量,再结合数据,基于下拉索的长度固定不变,利用求出来的每个xi来计算工作抛物面上主索节点的坐标,找出对应编号。
接下来解决馈源舱及基准反射球面的接收比,假设信号和电磁波的发射都是连续均匀分布的,将信号接收比转化为整个反射区域和接收区域的大小问题,同时将馈源舱与抛物面之间的信号反射问题简化在二维平面上解决。
(9)
其中,φ为工作抛物面的张角,r为抛物顶点到口径的垂直距离,A为圆弧形所围成的面积,k1、k2为接受信息面积的比值。
最终利用Matlab进行数值计算、分析得到调节前馈源舱的接受比为0.00159;调节后馈源舱的接受比为0.0526。因此,比较发现调节后馈源舱的电磁波信号接收比显著提高了,即得到天体电磁波经反射面反射后的最佳接收效果。
3 结论与展望
通过寻源和跟踪时“FAST”主动反射面的形状调节,目前已知FAST具有公里级高精度非接触式检测系统,可以实时检测(采集频段约为1 Hz)主索节点的三维位置,以及寻源和跟踪时可以按照检测结果调整索网结构下拉索的促动器,在天眼的工作中起到了决定性的作用。并且,寻源和跟踪系统的仿真过程在人类的日常生活中也起着难以代替的作用,例如采用FPGA的红外线雷达寻源与跟踪系统小车、医疗扫描器、射电望远镜等[5]。
