宽翼T形梁桥动力学理论与特性分析*
2013-09-17甘亚南石飞停
甘亚南 石飞停
(盐城工学院土木工程学院,盐城 2 24051)
宽翼T形梁桥动力学理论与特性分析*
甘亚南†石飞停
(盐城工学院土木工程学院,盐城 2 24051)
考虑了剪滞翘曲应力自平衡条件、剪切变形和剪力滞后效应等因素的影响,本文提出了一种对宽翼薄壁T形梁动力学特性的分析方法.分析中为了准确反应T形梁翼板的动位移变化,三个广义动位移被引入,且以能量变分原理为基础建立了T形梁动力反应的控制微分方程和自然边界条件,据此对T形梁的动力反应特性进行了分析,揭示了T形梁桥动力反应的规律.算例中,对比了考虑和不考虑剪滞翘曲应力自平衡条件对T形梁动力反应的影响,结果显示考虑剪滞翘曲应力自平衡条件的计算方法与有限元数值解吻合更好.
T形梁, 剪力滞后, 自平衡条件, 动力反应, 能量变分原理
引言
随着材料科学的发展,在桥梁工程中宽翼薄壁T形梁桥的应用前景更加广阔 .但是在对称弯曲状态下,宽翼薄壁T形梁存在剪力滞后效应现象 ,设计中如对其考虑不周,往往会在结构中产生一些横向、竖向和斜裂纹等病害.在对T形梁桥的力学分析中,由于国内外学者的不懈努力该类结构静力分析的解析法日趋完善,但是考虑剪滞翘曲应力自平衡条件、剪力滞后和剪切变形效应等因素,T形梁桥动力反应分析的解析法尚不充分.运营中,由于T形梁桥可能受到各种动荷载的作用,因而其动力学特性的研究更具理论和工程实际意义.但是,T形梁桥受剪力滞后效应的影响,经典强迫振动理论已不适用,因而动力学分析难度加大 .本文以能量变分原理为基础,运用直接解法对T形梁桥的动力反应进行了分析,本文理论为揭示T形梁桥动力反应规律奠定了一定的理论基础.
1 控制微分方程和自然边界条件
1.1 不计剪滞翘曲应力自平衡条件影响
1.1.1 体系的动能和势能
图1力系作用下图2所示的T形截面梁,在对称弯曲状态下,若结构的跨度为L,截面上的竖向动挠度为w1(x,t),轴向动位移u(x,y,z,t)满足下式[3,10]:

T形梁稳态振动时的各项势能
T形截面梁的荷载势能Vp为:

腹板和翼板的动应变能Vy为[2,6]:
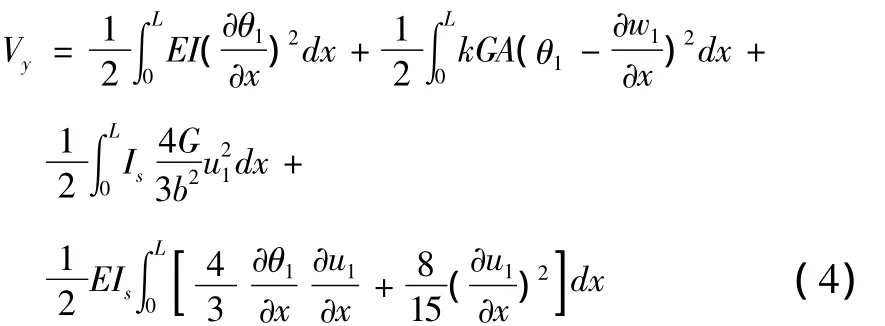
总势能为:VA=Vp+Vy(5)
结构总动能TA为[1,11]:

式中:x,z,y分别为通过截面形心的轴向、竖向和横向坐标;θ1(x,t)为T形截面绕y轴动转角;u1(x,t)为振动时剪力滞后效应引起翼板的纵向动位移差函数;I为全截面对中性轴的惯性矩;Is为翼缘板对中性轴的惯性矩;E,G分别为材料的杨氏弹性模量和剪切弹性模量;M1x(x,t)为翼板剪滞效应产生的动弯矩;MxA(x,t)为梁段端产生竖向转角θ1(x,t)的动弯矩;k为截面形状系数;A为T形梁截面面积;ρ为材料的质量密度;q(x,t)为分布简谐力.
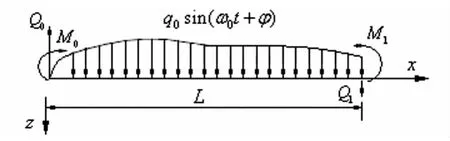
图1 坐标及荷载系统Fig.1 Coordinate and load system

图2 T形梁截面Fig.2 Cross section of T-beam
1.1.2 T形梁强迫振动微分方程及自然边界条件

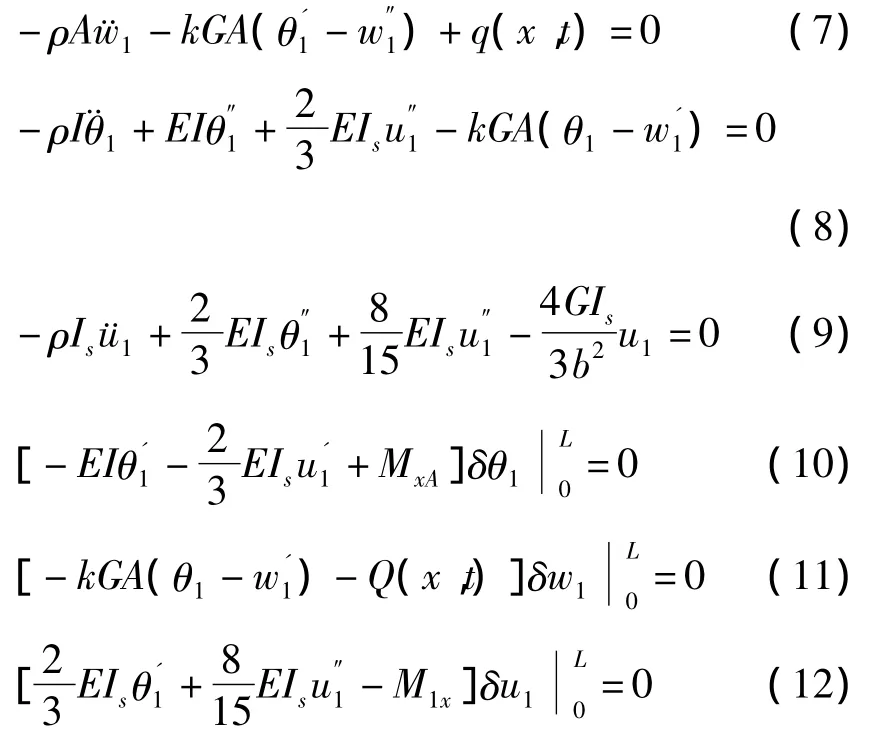
式(6)~(12)中,符号“.”和“'”分别表示对时间t和对坐标x求偏导数.
1.1.3 T形梁强迫振动微分方程的求解
若T形梁的强迫振动频率为ω0,即


由方程(8)得、的表达式,对方程(9)三次求导,将代入可得关于w1和θ1项的微分方程,将方程(7)代入,最后得新微分方程为:

对方程(13)分析可知,其特征方程解可为:

根据常微分方程组性质和方程(14)可以假设ψ1(x)解的形式,将方程(14)和ψ1(x)的假设式代入方程(7),根据恒等式原理求得ψ1(x)的常系数,ψ1(x)的解可表示为:
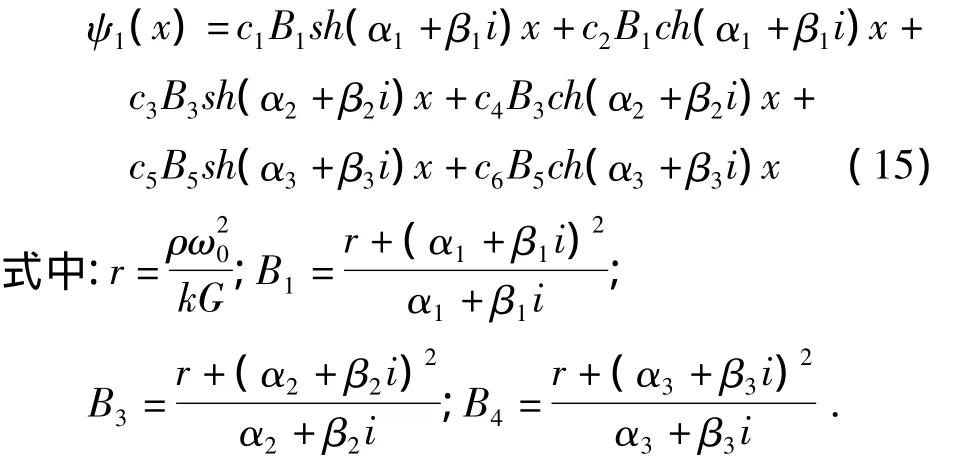
同样,根据方程(15)和常微分方程组性质可以假设U1(x)解的形式,将方程(15)和U1(x)的假设式代入方程(9),根据恒等式原理求得U1(x)的常系数,那么U1(x)的解可表示为:


1.2 考虑剪滞翘曲应力自平衡条件影响
1.2.1 体系的动能和势能
同样,图1力系作用下图2所示T形截面梁,在对称弯曲状态下,若结构的跨度为L,截面上的动挠度为w2(x,t),则剪滞效应引起翼板的翘曲位移为 η(x,y,z,t),且满足下式[1,10]:
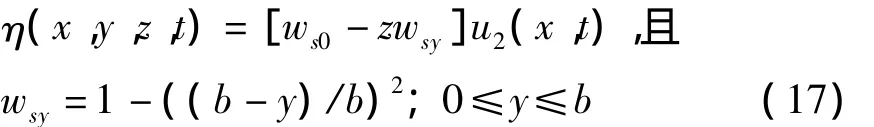
那么,由剪滞效应产生的动正应力和剪应为:

式中:ws0为常量,且ws0由 ∫AσsxdA=0确定为ws0=(4h1tb)/(3A).
式(19)满足截面平衡条件 ∫AτsxdA=0,那么剪滞效应产生的竖向动弯矩Msy可表示为:

总的竖向动弯矩及对应的动正应力分别为:

那么,垂直弯矩产生的动应变能为:

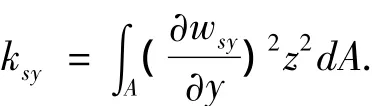
铁木辛柯剪切应变能为:
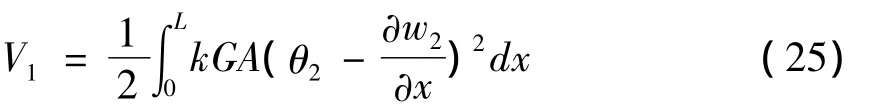
结构总动能为[1,11]:
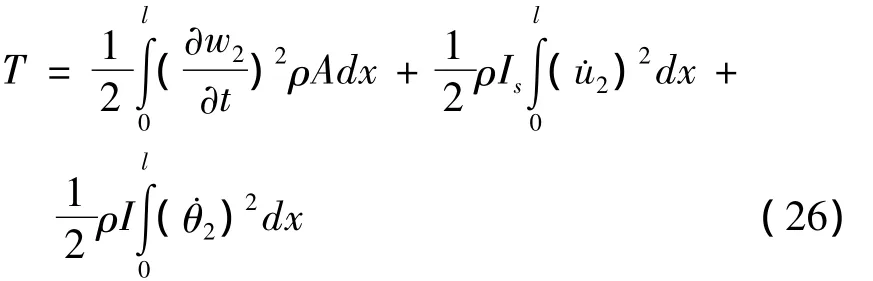
T形梁稳态振动时,考虑剪滞翘曲应力自平衡条件,其各项势能
T形截面梁的荷载势能Vq为:

系统总势能为:

式中:θz(x,t)为 T 形截面竖向动转角;u2(x,t)为振动时剪力滞效应引起翼板的纵向动位移差函数;且Iy;Isy;ksy;Is的含义如上表示,其它符号意义与不计剪滞翘曲应力自平衡条件时相同.
1.2.2 T形梁强迫振动微分方程及自然边界条件
由哈密顿原理δ-VB)dt=0,可推导出T形梁动力反应控制微分方程及自然边界条件为[12]:
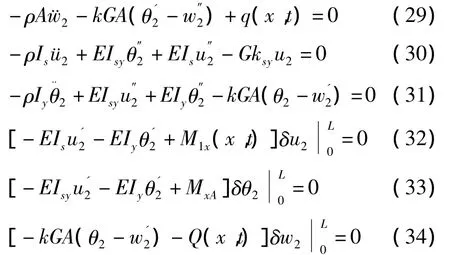
同样,式(18)~(34)中,符号“.”和“'”分别表示对时间t和对坐标x求偏导数.
1.2.3 T形梁强迫振动微分方程的求解
若T形梁强迫振动频率为ω0,那么

由方程(31)得的表达式,对方程(30)三次求导,且将代入可得关于w2和θ2项的微分方程,将方程(29)代入,可得新微分方程为:

式中:T=-
对方程(35)分析可知,其特征方程解可为:
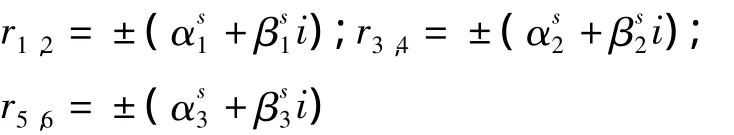
分析可知,方程(35)通解形式与方程(14)相同.且ψ2(x)与 ψ1(x),U2(x)与U1(x)解的表示形式亦相同,但此时
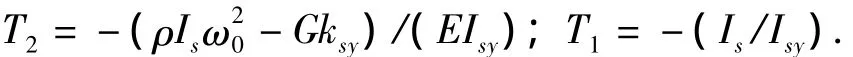
2 T形梁动力反应的简支边界条件
分析可知,两种情况下T形梁的边界条件相同,那么将W1(x),W2(x);ψ1(x),ψ2(x)和U1(x),U2(x)统一以W(x),ψ(x),U(x)的形式表示,则:
1)简支T形梁的位移和力学边界条件
A、简谐分布力

B、简谐集中力
对于简支T形梁,若跨间所受力为一简谐集中力,且集中力Pk=P0sin(ω0t+φ)左右相邻边界距离为Lk1和Lk2.如图3所示,则k点处还须引入下列连续边界条件为:
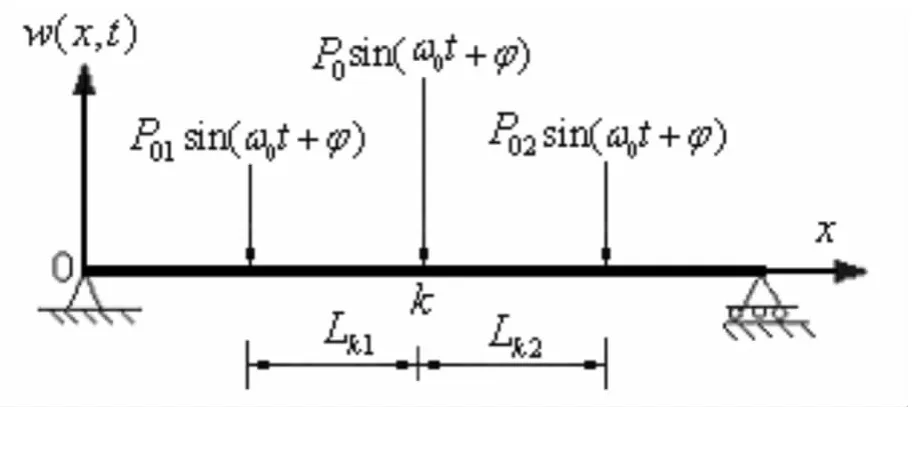
图3 算例中坐标系的约定Fig.3 The fixed coordinate system in the calculation examples

将方程式W1(x),W2(x);ψ1(x),ψ2(x);U1(x),U2(x)或其求导式代入边界条件(36)~(37),然后应用MATLAB软件和相应剪滞系数公式便可得到T形梁翼板简支边界条件下动剪滞效应的变化规律.
3 算例
对于T形截面梁,其材料和几何参数为:ρ=2500 kg/m3;E=3.5 ×104MPa;G=1.5 ×104MPa;tw=0.15 m;t=0.11 m;b=2.85 m.且梁高为h=1 m,简谐集中力幅值为P0=9800 N.则根据本文推导公式和其它方法可计算出T形梁的自振频率及E、F点动应力幅值.
在简支T形梁自振频率的求解过程中,令简谐分布力q(x,t)=0,然后应用MATLAB软件和边界条件(36)便可得到表1T形梁的自振频率值.表1表明:

表1 简支T形梁的固有频率(单位:Hz)Table 1 Natural frequency of simply-supported T-beam(unit:Hz)
1)本文T形梁自振频率计算值小于传统剪滞理论计算值,而传统剪滞理论计算值又小于铁木辛柯梁理论值,故由能量最低原理可以判断,在T形梁静、动力学分析中,本文计算理论优于传统剪滞理论,而传统剪滞理论又优于铁木辛柯梁理论;
2)本文自振特性分析为文献[1]的静力学分析提供了理论依据,且尽管三种理论自振频率计算值相差很小,但动力反应分析中本文计算理论有无实际意义尚需进一步的动力学分析加以验证;
3)T形梁自振特性受跨宽比的影响,跨宽比小自平衡条件和剪滞效应影响大,反之相反.
同样,简谐集中力作用下,在T形梁动应力幅值的求解过程中,应用MATLAB软件和边界条件(36)、(37)可得表2、表3和表4 T形梁的动应力幅值为:

图4 交点E、F为所求T形梁跨中动应力幅值位置Fig.4 Dynamic stress amplitude of middle-span of the T-beam located at the crossing points E and F
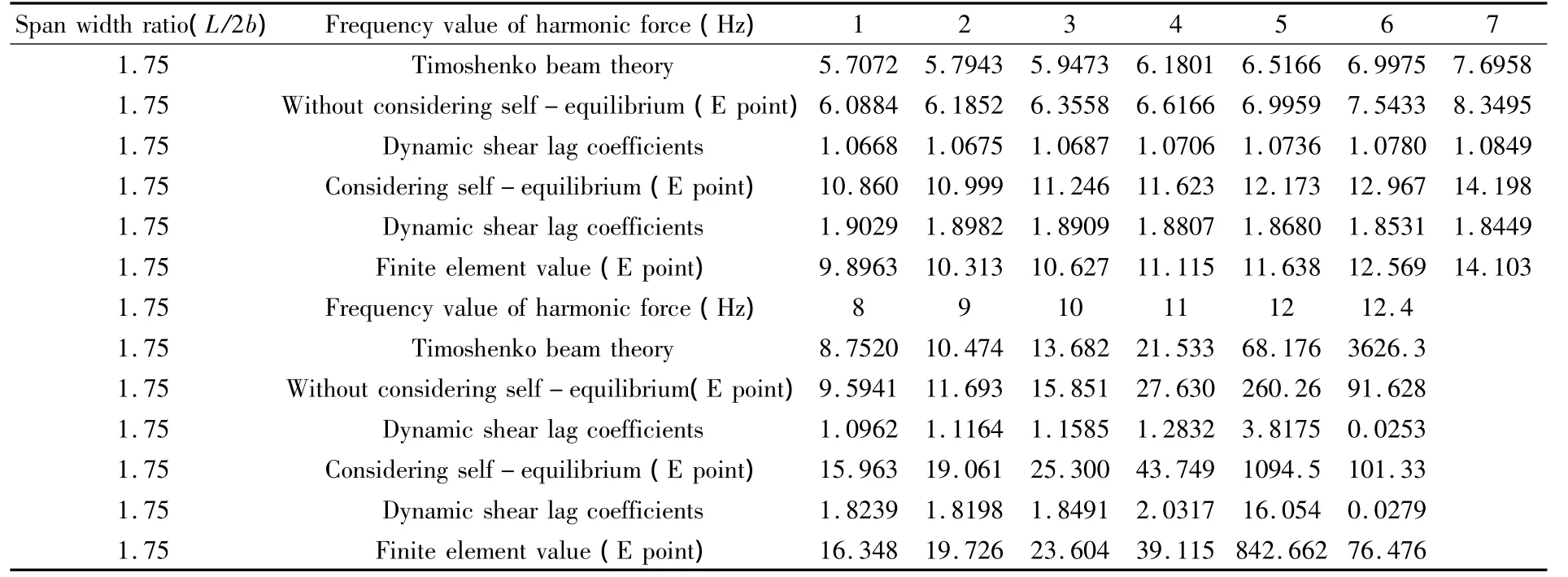
表2 简支T形梁E点的动应力幅值(单位:104Pa)(简谐集中力)Table 2 Dynamic stress amplitude of simply-supported T-beam located at the crossing point E(unit:104Pa)(Harmonic concentrated load)

表3 简支T形梁F点的动应力幅值(单位:104Pa)(简谐集中力)Table 3 Dynamic stress amplitude of simply-supported T-beam located at the crossing points F(unit:104Pa)(Harmonic concentrated load)

表4 简支T形梁E点的动应力幅值(单位:104Pa)(简谐集中力)Table 4 Dynamic stress amplitude of simply-supported T-beam located at the crossing point E(unit:104Pa)(Harmonic concentrated load)

图5 简支T形梁跨中E点动应力幅值比较图(L=10 m)(简谐集中力)Fig.5 The Comparison of dynamic stress amplitude of middle-span of simply-supported T-beam located at the crossing points E(L=10 m)(Harmonic concentrated load)
4 结论
本文理论系统分析了薄壁宽翼T形梁桥的动力学特性,结果显示出剪滞翘曲应力自平衡条件影响下T形梁自振频率计算值减小,并且自平衡条件对翼板正应力幅值计算值的影响更大,与传统剪滞理论计算值相比较,翼板与腹板相交处本文理论正应力幅值计算值明显增大,而远离腹板处翼板的正应力幅值计算值增幅较小.本文理论值与有限元数值解吻合较好,结果显示出剪滞翘曲应力自力平衡条件引入的必要性.
1 张元海,李乔.宽翼缘T梁剪滞效应分析的改进方法.兰州交通大学学报,2004,23(3):94~97(Zhang Y H,Li Q.A refined analysis method for shear lag effect of thinwalled T-Beams with wide flanges.Journal of Lanzhou Jiaotong University,2004,23(3):94 ~97(in Chinese))
2 Qi G S,Alexander C.Sordelis.Shear lag analysis of T,I and box beams.Structural Engineering,1990,116(5):1306~1318
3 Chang S T.Prestress influence on shear lag effect in continuous box girder bridge.Journal of Structural Engineering,ASCE,1992,118(11):3113 ~3121
4 吴亚平,赖远明.考虑剪滞效应的薄壁曲梁有限单元法.工程力学,2002,19(4):85~89(Wu Y P,Lai Y M.Finite element method considering shear lag effect for curved box beams.Engineering Mechanics,2002,19(4):85~89(in Chinese))
5 黄培元.普通钢筋混凝土连续箱梁桥开裂等问题的探讨.东北公路,2003,26(1):61~64(Huang P Y.Crack on common reinforced concrete continuous beam bridge.Northeastern Highway,2003,26(1):61 ~ 64(in Chinese))
6 甘亚南,周广春,赫中营.大悬臂板矩形截面箱梁动力反应的分析.振动与冲击,2010,29(11):61~65(Gan Y N,Zhou G C,He Z Y.Dynamic response analysis for a large cantilever rectangular box girder in consideration of shear lag effect.Journal of Vibration and Shock,2010,29(11):61~65(in Chinese))
7 康厚军,赵跃宇,王连华.斜拉桥中拉索对桥面动力特性的影响.动力学与控制学报,2007,5(1):44~49(Kang H J,Zhao Y Y,Wang L H.Theoretical considerations for effects of cables on deck of cable-stayed bridges.Journal of Dynamics and Control,2007,5(1):44 ~49(in Chinese))
8 陈政清,牛华伟,刘志文.平行双箱梁桥面颤振稳定性试验研究.振动与冲击,2006,25(6):54~58(Chen Z Q,Niu H W,Liu Z W.Expermental study on flutter stability of parallel box-girder bridges.Journal of Vibration and Shock,2006,25(6):54 ~58(in Chinese))
9 丁虎,胡庆泉,陈立群.运动车辆梁模型的横向振动频率及模态.动力学与控制学报,2011,9(1):44~48(Ding H,Hu Q Q,Chen L Q.Natural frequencies and model function of transverse vibration of beam modal for moving vehicles.Journal of Dynamics and Control,2011,9(1):44~48(in Chinese))
10 甘亚南,周广春.薄壁箱梁纵向剪滞翘曲函数精度选择的研究.工程力学,2008,25(6):100~106(Gan Y N,Zhou G C.An approach for precision selection of longitudinal shear lag warping displacement function of thinwalled box girders.Engineering Mechanics,2008,25(6):100~106(in Chinese))
11 Clough R.结构动力学.王光远等译.高等教育出版社,2006.11(Ray Clough.Dynamics of structures.Wang G uangyuan translation,and so on.Higher Education Press,2006.11(in Chinese))
12 胡海昌.弹性力学的变分原理及其应用.北京:科学出版社,1981(Hu H C.Principle of variations and its applications in mechanics of elasticity.Beijing:Science Press,1981(in Chinese))
*This Project supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China(13KJB560014)
† Corresponding author E-mail:gyn-12@163.com
ANALYSIS ON DYNAMIC THEORY AND CHARACTERISTICS OF THIN-WALLED T-BEAMS WITH WIDE FLANGES*
Gan Yanan†Shi Feiting
(School of Civil Engineering and Architecture,Yancheng Institute of Technology,Yancheng224051,China)
In consideration of shear deformation and shear lag effects,A new warping displacement mode of T-beams is chosen to meet the axial self-equilibrium condition for corresponding stress,this paper proposes an approach of analyzing the dynamic characteristics of thin-walled T-beams with wide flanges generally used in engineering.three generalized displacement functions are employed in analyzing dynamic response of the thin-walled T-beams by calculus of variations,the differential equations and the corresponding natural boundary conditions of the T-beams are induced based on the minimum potential principle,and the dynamic characteristics of thinwalled T-beams are discussed.The calculation examples compare the finite solid element solutions with the analytical solutions,and the analytical solutions in consideration of the axial self-equilibrium condition is still more identical with the finite solid element solutions,the formulas obtained in this study strengthen the theoretical foundation for further research of dynamic characteristics of the structures.
T-beam, shear lag effect, self-equilibrium condition, dynamic response, energy-variation principle
02 July 2012,
22 September 2012.
10.6052/1672-6553-2013-054
2012-07-02 收到第 1 稿,2012-09-22 收到修改稿.
*江苏省高校自然科学研究(13KJB560014)项目
E-mail:gyn-12@163.com
