基于CFD/CSD方法的亚音速平板结构气动弹性分析*

谌胜 刘春川 李凤明†

(1．哈尔滨工业大学航天学院，哈尔滨 1 50001)(2．哈尔滨工业大学机电学院，哈尔滨 1 50001)

基于CFD/CSD方法的亚音速平板结构气动弹性分析*

谌胜1刘春川2李凤明1†

(1．哈尔滨工业大学航天学院，哈尔滨 1 50001)(2．哈尔滨工业大学机电学院，哈尔滨 1 50001)

采用CFD/CSD双向流固耦合算法研究平板结构的气动弹性耦合特性．首先，采用CFD/CSD算法计算平板结构的颤振临界速度，并与已有文献中的实验结果进行比较验证．然后，分别对简支和固支边界条件的三维平板结构进行气动弹性特性分析，计算不同约束情况下流场分布的变化和平板结构的位移响应．同时还考虑加肋和结构材质对平板结构气动弹性特性的影响．

平板结构， 亚音速气流， 气动弹性耦合特性， CFD/CSD算法， 时域响应

引言

随着航空工业的迅猛发展，结构的气动弹性问题受到了研究人员的广泛关注．目前，针对结构气动弹性方面的研究，已经获得了很多的成果，但主要集中在跨音速与超音速的范围内．1940年，美国Tacoma悬索桥在非常低风速(18m/s)气流的作用下发生倒塌［1］，使得人们认识到了气动弹性问题有可能在亚音速气流作用下明显的表现出来．另外，由于工程的要求，需要在复杂的外界条件下减轻结构的质量，这样就导致气动弹性问题越来越突显．

关于平板颤振的问题，国内外已有很多研究成果，其中以超声速的研究居多［2－4］．在亚音速平板颤振研究方面，美国学者Dowell对前人的研究成果进行了总结［5－7］．给出了线性和非线性壁板颤振的计算模型，以及平板结构亚音速和跨音速气动力的计算方法．之后国内外有很多学者采用Galerkin法、微分求积法等方法对亚音速平板结构的气动弹性问题进行了研究［8－11］．

气动弹性问题除了上述研究中使用的经典方法以外，还发展出了一些数值计算方法．其中运用最为广泛的就是应用于飞行器颤振分析的偶极子网格法(DLM)，这是一种计算气动力的简化数值方法，MSC．NASTRAN有限元分析软件的气动弹性模块就是使用的偶极子网格法．但这种算法对于固体场和流体场都有很强的限制，例如该方法只适用于线性、势流的气动力模型，无法考虑机翼结构厚度的迎角，对于其它复杂结构的模型也无法处理［12］．近年来，随着计算机技术的快速发展，计算流体动力学(CFD)和计算固体动力学(CSD)都得到了广泛的应用．但是，由于流体域和固体域的基本方程有很大差别，在数学特性上也完全不一样．因此，建立整体的流固耦合方程并耦合求解只能适用于简单问题的科学研究，无法进行复杂问题的大规模计算．此后，基于CFD/CSD的双向迭代算法逐渐运用于求解耦合场的问题．

基于CFD/CSD的流固耦合算法早期主要用于计算固体和液体的耦合作用．如水下导弹的研究、船和水的耦合作用等，后来逐渐应用于结构的气动弹性问题分析．Bhardwaj 和 Kapania［13，14］采 用 CFD/CSD的耦合算法对机翼结构进行了静气动弹性计算，并与实验进行对比，验证了CFD/CSD算法对静气动弹性问题的计算准确性．Biedron和Lee［15］采用非结构化网格建立了UH－60A型机翼的模型，分析了其在高速运行时的流固耦合问题．另外，国内外很多学者采用CFD/CSD算法对AGARD445．6型机翼的气动弹性问题进行了计算，并与实验结果以及理论定性分析结果进行对比验证［12，16－19］．除了机翼结构之外，还有学者使用CFD/CSD算法对涡轮叶片的颤振特性进行了研究［20，21］．总体来说，目前基于CFD/CSD方法的气动弹性问题研究主要集中在飞机机翼结构上，对于平板等其它结构的研究较少．

本文采用CFD/CSD双向迭代算法分析亚音速气流作用下平板结构气动弹性耦合特性，计算了平板结构的颤振临界速度，并与已有的实验结果进行对比，验证了采用CFD/CSD算法分析结构气动弹性耦合特性的有效性．计算了加肋三维平板结构气动弹性瞬态响应，并讨论了不同边界条件对平板结构气动弹性响应的影响．本文提出的研究方法为研究复杂平板结构及其组合结构的气动弹性耦合振动特性提供了一种有效的思路．

1 CFD/CSD算法的基本理论

1．1 基本思想

流体域和固体域分别采用有限单元法和有限体积法单独求解，然后通过数据交换技术在流固交界面处耦合迭代，最后求得整个域的变量．流固耦合计算的过程与时间相关，因此是一个典型的瞬态动力学问题．

固体场的计算主要采用有限单元法进行结构动力学的求解．采用有限单元法对固体结构进行离散．在动力学分析中引入了时间坐标，因此这是一个四维(x，y，z，t)问题．通过有限元的离散，连续性结构的无限维问题就变成与节点位移有关的有限维数的问题．写成矩阵表达式:

M¨a(t)+Ca(t)+Ka(t)=Q(t)(1)式中a为节点位移列向量，M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，Q为气动压力．式中的变量均与时间有关．式(1)是一个二阶常微分方程组，采用Newmark数值积分方法可以对其进行求解．

流体场的计算则采用有限体积法．有限体积法能保证离散单元的守恒性，且离散方程物理意义清晰，因此在流体计算时有限体积法应用最为广泛．与有限单元法相似，有限体积法也是离散求解的思想．有限体积法将流体计算区域划分成若干个控制体，每个控制体都由一个节点代表，通过对控制体进行积分从而达到离散化的目的．本文主要采用二阶迎风格式对流体场进行离散处理．

1．2 计算流程

图1是CFD/CSD双向流固耦合算法的流程图．首先，由CFD方法计算出流体域的压力分布，然后在流固交界面处将流体计算出的压力施加到固体域上，对固体进行CSD瞬态动力学分析．固体产生变形以后，使得流体边界发生变化，通过动网格技术产生新的流体域，计算新的流场分布，然后再作用到固体上，依次循环．当前后两次的流场参数分布以及固体场参数分布的差值小于某一设定数值时，则认为迭代收敛．之后进入下一个时间步计算，计算方法与上一时间步相同．最终计算完成以后可以得到固体场和流体场在每个时刻的结果，如压力分布、速度、位移等．

固体场产生变形传递给流体场时涉及到动网格的技术．本文主要使用基于弹性变形的网格调整方法．基于弹性变形的网格调整方法将整个网格视为一个弹簧系统，通过边界节点上的位移来调整整个流体域的节点位置，这样的方法不改变网格之间的连贯性．将节点想象成一个质点，节点间的连线想象成一个弹簧，边界节点上的位移导致与节点相连的“弹簧”产生相应的变形，从而通过整个网格传播出去．每个节点周围的“弹簧”对节点产生的力是平衡的．在边界位移已知的情况下，可通过Jacobi矩阵对流域内部所有节点位移进行求解，从而得到网格变形以后的节点位移．

图1 CFD/CSD算法流程图Fig．1 The flow diagram of CFD/CSD algorithm

2 CFD/CSD算法验证

本文选取美国学者 Dugundji和Dowell［22］文献中的结果进行对比，以验证算法的有效性．文献［22］中计算了两边简支的弹性支撑平板结构在亚音速气流作用下的颤振特性．平板材料是铝，其长2．64m，宽 0．61m，厚 0．46mm．弹性支撑的弹性系数K=18879．91N/m2．文献中实验测得的颤振临界速度为42．47m/s．对于线性颤振问题，当来流速度大于颤振临界速度时，位移响应发散;小于颤振临界速度时位移响应收敛;来流速度恰好等于颤振临界速度时，位移响应处于等幅运动的临界状态．本文基于以上原则判断结构的颤振临界速度．

本文采用CFD/CSD算法对上述模型进行计算．图2是通过CFD/CSD算法计算出的平板中点时域响应曲线．如图2(a)所示，初始时刻平板上作用有一个外激励，平板中点位移初始有一些波动，位移大致趋于衰减．t=1s左右运动趋于稳定，随着时间的增长，位移持续发散．因此可以说明，40m/s是大于颤振临界速度的．但此时位移发散的速率不大，此时比较接近临界速度．图2(b)中当来流速度为37m/s时，位移初始衰减然后趋于小幅的等幅运动．因此，从图2可以判断出颤振点在37m/s附近，与文献［22］中得到的颤振临界速度42．47m/s是很接近的．这表明，采用CFD/CSD算法对平板结构进行气动弹性分析是可行的．

图2 平板中点处时域响应Fig．2 The time domain responses at the midpoint of plate

3 算例分析

在实际工程中很多平板结构通常可以简化成四边简支或四边固支的情况，本节针对加肋板结构的四边分别为简支和固支情况进行分析研究．

图3 计算模型图Fig．3 The calculating model

图4 四边简支加肋平板压力云图Fig．4 The pressure cloud pictures of simply supported ribbed plate

图3(a)是平板结构和流体场的计算模型．平板长L=1m，宽b=1m，厚度h=3mm，平板结构沿X方向加了三根肋条，其尺寸为高2cm，宽1cm．来流速度为140m/s，采用层流理论进行计算．左边为流体入口，右边为压力出口，平板处为流固耦合交界面，其它部分为默认壁面设置．平板初始时刻作用有均布压力p=1000Pa，作用时间0．01s．

图3(b)是流场网格划分情况．流场是规则的矩形，可以方便地进行结构化网格划分，将流场分割成九个矩形以便于对网格尺寸进行控制．距离平板近的流域网格细分以较好地捕捉流场变化，距离平板较远的地方由于流场变化较小，采用较粗的网格即可满足计算要求．这样的网格划分既能满足计算精度要求，又能合理控制单元数，提高计算效率．该模型流场网格共有约32万个网格．

首先考虑四边简支的情况，计算中四边简支的加肋平板结构材料分别取为钢和铝合金．

图4是四边简支加肋钢板的计算结果，图中显示了不同时刻流体域中间剖面和平板上的压力分布．其中为了便于观察，平板的变形经过了放大处理．图4(a)中由于初始时刻的压力作用，变形较大，流场的变化也比较大．平板中间处于正压区，边界处有少数区域属于负压区．Y=0．5m的中间剖面上，平板附近的压力变化比较明显，平板以外的流域压力变化较小．当平板位移运动到Z轴正方向时，压力分布则正好相反．对于图4(b)，当时间t=0．25s时，平板的位移已经很小，流场的压强也相对较小．

图4(c)是t=0．25s时平板上的压力分布图．由于整个模型以及边界条件、初始条件都是关于X方向对称的，因此流场分布基本上也是关于X方向对称．这一点可以从图4(c)和图4(d)中看出．图4(d)中远离平板的剖面上压力变化较小，压力值也比较小．说明平板的运动变形对于远处的流场影响较小，在建模时将流场的区域取足够大时就能够得到更接近于真实的结果．从图4中还可以明显看到，流场沿Y方向是变化的，并且变化比较明显．因此，在对平板结构进行气动弹性分析时，如果平板结构是三维模型，采用二维流场模型进行流固耦合计算是不够的，将会产生较大误差．

本文对四边简支的加肋铝合金板进行了同样的计算，其流场分布规律与钢板类似．图5是四边简支加肋平板结构中点处的响应曲线，其中图5(a)材料为钢，图5(b)材料为铝合金．由于边界条件为简支，其整体结构刚度比较大，两种材料的平板结构位移响应幅值都比较小，加肋钢板的最大位移幅值在1mm左右，铝合金板的最大位移幅值在2．5mm左右．而且两者运动趋势均为收敛，这表明在来流速度为140m/s时，两种材质的平板结构均未发生颤振．

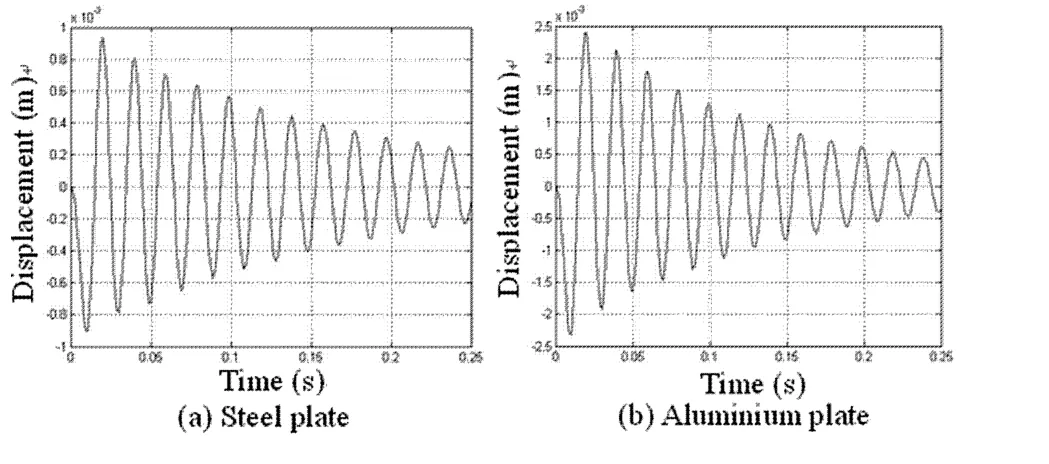
图5 四边简支加肋平板中点的时域响应Fig．5 The time domain responses at the midpoint of simply supported ribbed plate

下面对四边固支边界条件下的钢板和铝合金板进行计算．如图6为四边固支加肋钢板流固耦合计算的压力分布云图．分布状况与四边简支板基本类似，但由于固支板的刚度较大，因此平板结构位移响应非常小，由此导致流场压强也非常小．当时间t=0．1s时，平板运动产生的压强只有2Pa左右，而到t=0．25s时位移已经接近于零，此时流场的变化非常小，压强数值也趋近于零．

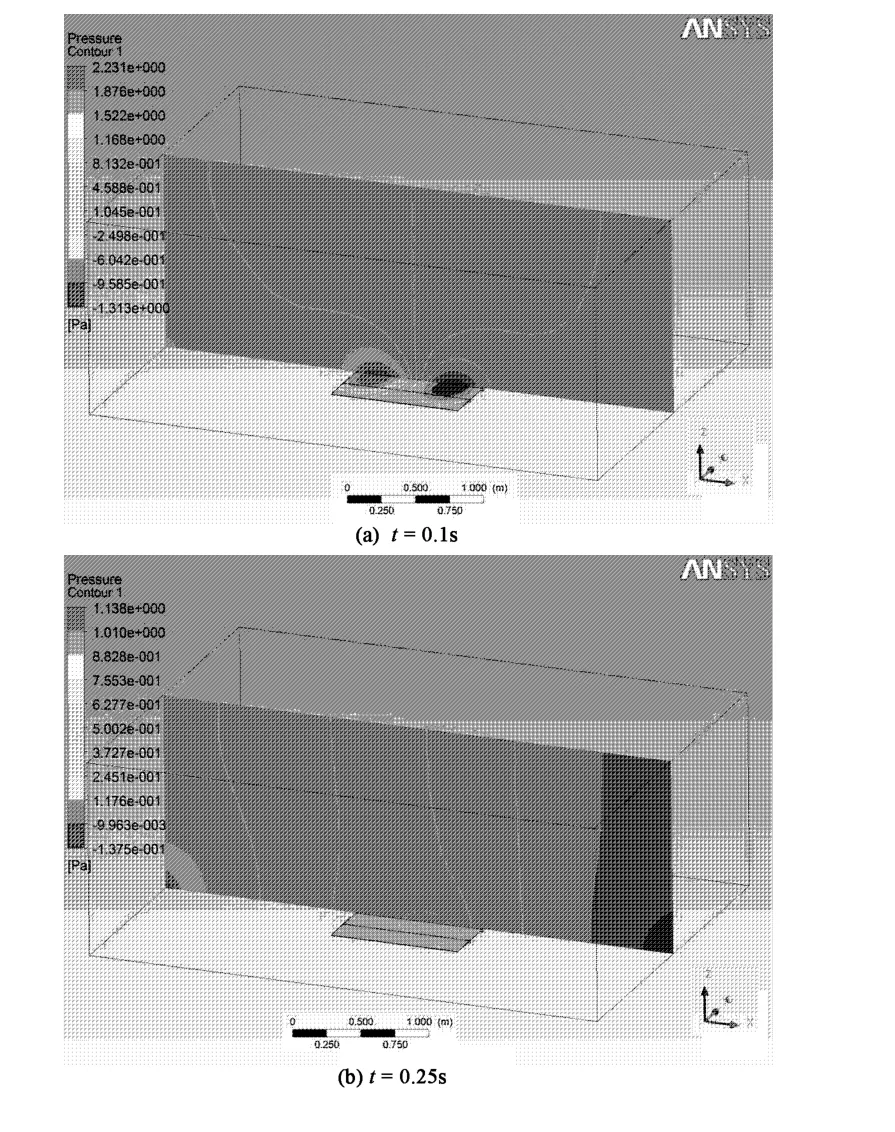
图6 四边固支加肋平板压力分布云图Fig．6 The pressure cloud pictures of clamped ribbed plate

图7是气动力作用下四边固支板中点的响应曲线．由于固支加肋板的刚度比较大，因此位移幅值很小，最大值分别只有0．1mm和0．2mm．在初始冲击载荷的作用下，响应曲线中第一个周期位移响应相对较大，随着时间的增长，响应逐渐衰减，并且很快就衰减到位移接近于零．此后，平板和来流的相互作用越来越小，逐渐衰减至最后静止．此处研究结果表明，当增强结构的约束条件，也即增大结构刚度时，对结构的气动弹性耦合效应将有明显的提高．

图7 四边固支加肋平板中点的时域响应Fig．7 The time domain responses at the midpoint of clamped ribbed plates

4 结论

本文主要对CFD/CSD数值计算方法进行了对比验证，并采用CFD/CSD算法对平板结构的气动弹性问题进行了研究．首先将CFD/CSD数值计算结果与已有文献的实验结果进行了比较，验证了CFD/CSD算法对于计算气动弹性问题的适用性．然后分别对三维简支和固支约束条件的平板结构进行计算，分析了不同情况下流场的变化和平板结构的位移响应．通过分析，得到以下结论:

(1)CFD/CSD双向流固耦合算法适用于计算结构的气动弹性问题，计算结果较好．其优点是受气动力模型和结构模型的限制较少，适用于工程问题中的大规模计算，并且其计算结果以图形的方式直观显示，可以为理论分析提供参考．其不足之处是计算量大，寻找颤振点花费时间较多，算法还有待进一步改进提高．

(2)在对三维平板结构进行气动弹性分析时，如果流场采用二维模型是远远不够的，将会产生较大误差．

(3)当增大结构刚度时，对结构的气动弹性耦合效应将有显著影响．其中，钢材比铝合金材料的结构位移小，四边固支平板结构的位移响应较四边简支平板结构衰减更快．

1 伏欣H W著，沈克扬 译．气动弹性力学原理．上海:上海科学技术文献出版社，1982(Fxin H W(written)，Shen K Y(translation)．Principle of aero－elastic mechanics．Shanghai:Shanghai Science and Technology Literature Press，1982(in Chinese))

2 Lee I，Lee D M，OH I K．Supersonic flutter analysis of stiffened laminated plates subject to thermal load．Journal of Sound and Vibration，1999，224(1):49～67

3 Li F M．Active aeroelastic flutter suppression of a supersonic plate with piezoelectric material．International Journal of Engineering Science，2012，51:190～203

4 Song Z G，Li F M．Active aeroelastic flutter analysis and vibration control of supersonic composite laminated plate．Composite Structures，2012，94:702～713

5 Dowell E H．Panel flutter:a review of the aeroelastic stability of plates and shells．AIAA Journal，1970，8(3):385～399

6 Dowell E H．A modern course in aeroelasticity．Kluwer Academic Publishers，2004

7 Dowell E H．Aeroelasticity of plates and shells．Noordhoff International Publishing，1975

8 Tang D，Dowell E．H．Limit cycle oscillations of two－dimensional panels in low subsonic flow．International Journal of Non-Linear Mechanics，2002，37:1199～1209

9 Tang D M，Yamamoto H，Dowell E H．Flutter and limit cycle oscillations of two－dimensional panels in three－dimensional axial flow．Journal of Fluids and Structures，2003，17:225～242

10 Eloy C，Souilliez C，Schouveiler L．Flutter of a rectangular plate．Journal of Fluids and Structures，2007:23:904～919

11 李鹏，杨翊仁，鲁丽．微分求积法分析二维亚音速壁板的失稳问题．动力学与控制学报，2012，10(1):11～14(Li P，Yang Y R，Lu L．Instability analysis of two－dimensional thin panels in subsonic flow with differential quadrature method．Journal of Dynamics and Control，2012，10(1):11～14(in Chinese))

12 卢学成，叶正寅，张陈安．基于ANSYS/CFX耦合的机翼颤振分析．计算机仿真，2010，27(9):88～91(Lu X C，Ye Z Y，Zhang C A．A coupled ANSYS/CFX method for the wing flutter calculation．Computer Simulation，2010，27(9):88～91(in Chinese))

13 Bhardwaj M K，Kapania R K．A CFD/CSD interaction methodology for aircraft wings．NASA Technical Reports，1998

14 Kapania R K，Bhardwaj M K．Aeroelastic analysis of modern complex wings．NASA Technical Reports，1996

15 Biedron B T，Lee R E M．Computation of UH－60A airloads using CFD/CSD coupling on unstructured meshes．67th American Helicopter Society International Annual Forum 2011，2011

16 Liu F，Cai J，Zhu Y，et al．Calculation of wing flutter by a coupled CFD－CSD method．38th Aerospace Sciences Meeting＆ Exhibit，2000

17 Liu F，Cai J，Zhu Y，et al．Calculation of wing flutter by a coupled fluid－structure method．Journal of Aircraft，2001，38(2):334～342

18 Xi R，Jia H．A strong coupled CFD－CSD method on computational aeroelastity．Mechanic Automation and Control Engineering，2011:5512～5515

19 曾宪昂，徐敏，安效民等．基于CFD/CSD耦合算法的机翼颤振分析．西北工业大学学报，2008，26(1):79～82(Zeng X Y，Xu M，An X M，et al．Wing flutter analysis using CFD/CSD algorithm．Journal of Northwestern Polytechnical University，2008，26(1):79 ～ 8 2(in Chinese))

20 Zhang J P，Pan L L．Three－dimensional modeling and aeroelastic coupling analysis for the wind turbine blade．World Non－Grid－Connected Wind Power and Energy Conference，2009:24 ～26

21 张兴国，刘锋，张陈安．基于CFD技术的叶片颤振分析．航空计算技术，2009，39(4):75～78(Zhang X G，Liu F，Zhang C A．Flutter computation of turbomachinery blades based on CFD．Aeronautical Computing Technique，2009，39(4):75～78(in Chinese))

22 Dugundji J，Dowell E H，Perkin B．Subsonic flutter of panels on continuous elastic foundations．AIAA Journal，1963，1(5):1146～1154

*The project supported by the National Basic Research Program of China(2011CB711100)and the National Natural Science Foundation of China(11172084，10672017)

† Corresponding author E－mail:fmli@hit．edu．cn

AEROELASTIC ANALYSIS OF PLATE STRUCTURES IN SUBSONIC AIR FLOW BASED ON CFD/CSD ALGORITHM*

Shen Sheng1Liu Chunchuan2Li Fengming1†
(1．School of Astronautics，Harbin Institute of Technology，Harbin150001，China)(2．School of Mechatronic Engineering，Harbin Institute of Technology，Harbin150001，China)

The two－way fluid－structure coupling algorithm，i．e．the CFD/CSD algorithm，is used to study the aeroelastic coupliing characteristics of plate structures in subsonic air flow．Firstly，the flutter critical velocity of the plate structure is computed employing the CFD/CSD algorithm．The results obtained by the CFD/CSD are verified by comparing with the experiment results in the open literature．Secondly，the aeroelastic characteristics for three－dimensional plate structures with simply supported and clamped edges are analyzed．The variation of flow field distribution and the displacement responses of the plate under different restricted conditions are claculated．Meanwhile，the influences of the stiffener and structural material parameters on the aeroelastic characteristices of the plate structure are also considered．

plate structure， subsonic air－flow， aeroelastic coupling characteristics， CFD/CSD algorithm，time domain response

5 July 2012，

15 November 2012．

10．6052/1672－6553－2013－037

2012－07－05 收到第 1 稿，2012－11－15 收到修改稿．

*国家重点基础研究发展计划(973计划)(2011CB711100)和国家自然科学基金资助项目(11172084，10672017)

E－mail:fmli@hit．edu．cn