三维实体转子系统热－结构耦合响应分析*

李岩 袁惠群，2† 梁明轩 贺威

(1．东北大学机械工程与自动化学院，沈阳 1 10004)(2．东北大学理学院，沈阳 1 10004)(3．沈阳农业大学高等职业技术学院，沈阳 1 10122)

三维实体转子系统热－结构耦合响应分析*

李岩1袁惠群1，2†梁明轩1贺威3

(1．东北大学机械工程与自动化学院，沈阳 1 10004)(2．东北大学理学院，沈阳 1 10004)(3．沈阳农业大学高等职业技术学院，沈阳 1 10122)

以某型航空发动机高压转子系统为研究对象，基于不均匀分布稳态温度场，建立了某高压转子系统三维实体单元有限元模型以及稳态温度场下转子系统热－结构耦合振动方程，利用热－结构－动力学耦合理论，采用间接耦合法，通过稳态温度场分析和静力分析生成热应力，然后进行预应力模态分析，最后利用模态叠加法进行不平衡量和热弯曲耦合响应分析，实现热－结构－动力学耦合计算．通过稳态温度场对典型级盘稳态响应影响的分析以及不平衡量与热弯曲耦合稳态响应分析，发现耦合响应对转子系统各级盘的振动响应有较大影响．

三维转子系统， 有限元法， 固有频率， 稳态温度场， 热弯曲耦合响应

引言

航空发动机在启动、停车以及高速运转的过程中温度的变化非常明显．由于温度分布不均衡产生的热应力，导致转子系统产生一定变形，使转子系统的刚度矩阵重新分布．转子系统的材料物性参数也会随着温度而变化，对转子的振动特性也必将产生一定的影响［1］．目前，对于转子系统热振动的研究主要集中在均匀温度场引起的热膨胀［2］．晏水平等［3］人探讨了弹性模量随温度的变化对于转子系统振动特性的影响，采用轴系的温度分布为常量的基本假设，忽略温度对振动的影响．贺威等［4］人利用传递矩阵法，研究了某型航空发动机多盘转子系统热弯曲稳态及瞬态响应，转子热弯曲量的确定并没有考虑转子温度场情况．目前，国内外对以真实温度场为基础，利用热－结构－动力学耦合理论分析三维实体转子系统的振动特性的研究还很少．朱向哲等人［5］虽然对稳态温度场对某汽轮机转子系统的固有频率的影响进行了探讨，但是其所建立的模型仍然是传统的盘轴系统或者关于梁的热振动问题，与实际结构有很大差别．因此，有必要对由航空发动机转子系统的实际结构而建立的三维实体模型的热振动特性进行深入的研究，分析稳态温度场对转子系统振动特性的影响以及不平衡量和热弯耦合响应，以便找出影响其热振动特性的敏感因素．

1 三维实体转子系统热－结构耦合模型

航空发动机等实体结构由于形体及温度场较复杂，难以简化为平面问题或轴对称问题，必须按空间问题求解．为了保证必要的计算精度，必须采用密集的计算网格，这样一来，节点数量将很多，方程组十分庞大．如果采用高次位移模式，单元中的应力是变化的，就可以用较少的单元、较少的自由度而得到要求的计算精度，因此，采用20结点等参数单元．

1．1 三维转子系统有限元动力学模型

1)位移模式．20节点等参数单元，每个节点有三个位移分量

式中，N为20节点等参元的形函数表达式为:

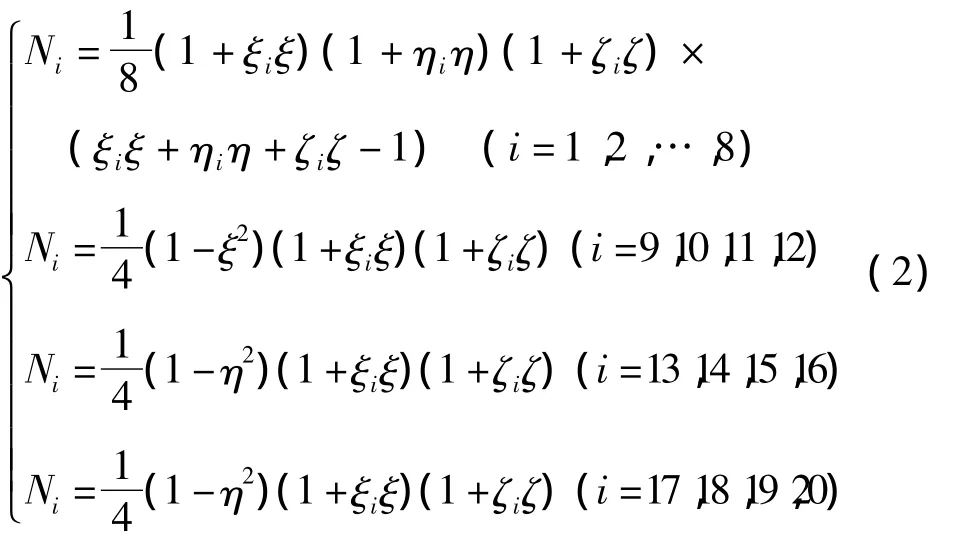
其中:ξi、ηi、ζi分别为节点的局部坐标．

总体坐标与局部坐标的转换关系，即Jacbi为:

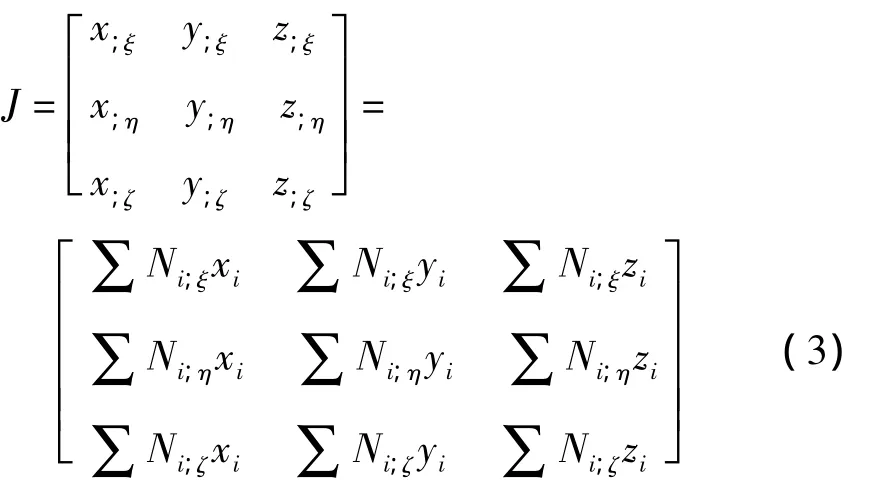
逆变换的Jacbi为

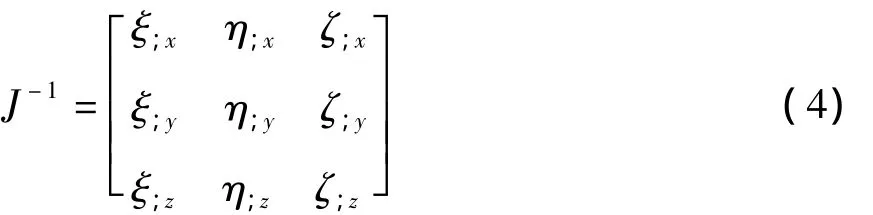
其中:ξ;x…ζ;z为|J|的代数余子式除以|J|

每个单元共有60个节点位移分量，表示为向量

2)单元应变．在空间应力问题中，每个点具有6个应变分量

3)单元应力．单元应力可用节点位移表示为

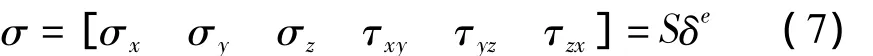
其中，应力矩阵S=DB，弹性矩阵D为

其中:E为弹性模量;μ为泊松比．

4)单元刚度矩阵．由虚位移原理，可得到单元刚度矩阵:

5)三维转子系统有限元单元体动力学方程．为了满足后续的响应与故障分析的研究需要，本文采用三维实体有限元分析转子系统的振动特性．

在离心力场中运动物体受惯性力、阻尼力作用，可以导出转子有限单元体运动微分方程为:

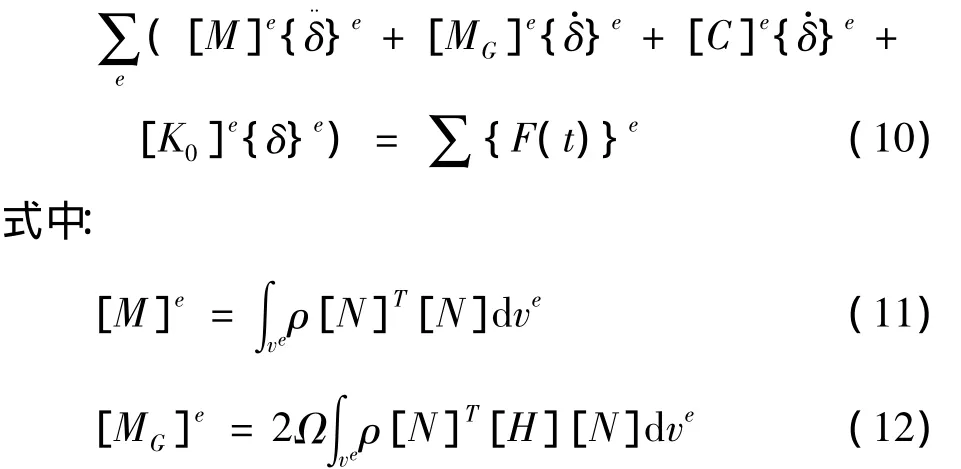
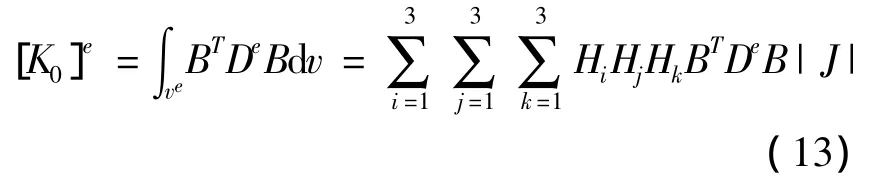
其中:{F(t)}e为单元的激振力;［M］e为单元的质量矩阵;［MG］e为单元哥氏力矩阵;［N］为单元形状函数矩阵;{δ}e为单元节点位移向量，［K0］e为单元线刚度矩阵;［C］e为阻尼矩阵;［H］为转轴方向的单位矢量构成的矩阵;

式(14)是适用于转子静力和动力分析的有限元方程．

1．2 三维实体转子系统热-结构耦合模型振动方程

对于稳态加热或冷却的情况，在转子表面的轴向和切向热应力，主要是由于节点温度的不均匀变化，转子的不均匀膨胀受到约束限制而产生的热应力．单元热应力基本方程:

式中:E(t)为随温度变化的弹性模量，α为热膨胀系数为不同工况转，T0为初始环境温度子温度，其它符号同前．

根据D＇Alembert原理，温度应力作用的转子振动方程为:

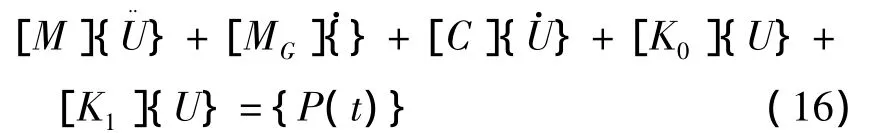
式中，［M］、［MG］、［C］、［K0］分别是转子系统的质量矩阵、哥氏力矩阵、阻尼矩阵和刚度矩阵;{U}、}、}分别是节点位移向量、速度向量和加速度向量;{P(t)}为不平衡荷载向量．

对于转动的转子系统来说，任意点在工作过程中产生的位移向量{U}可以看成两部分组成:

式中:{δ}表示从原始形状变形到离心力场平衡位置的位移，{δT}表示温度应力引起的变形．静力分析时则有

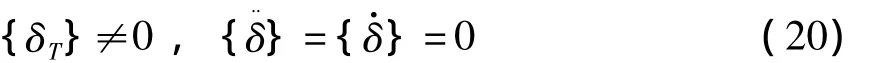
由于温度载荷的存在，转子受力产生变形，因此，导致转子系统的刚度矩阵发生变化，式(16)变为

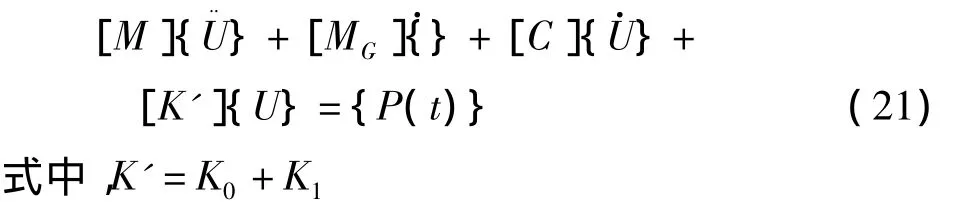
本文利用Ansys软件，采用间接耦合法，先进行稳态温度场分析，再进行静力分析生成热应力，然后通过设置预应力选项生成总刚度矩阵K'，进行模态分析，最后利用模态叠加法进行不平衡量和热弯曲耦合响应分析，实现热-结构-动力学耦合计算．

2 三维实体转子系统热振动特性分析算例

图1为某航空发动机双转子系统中的高压转子，长度为1．05m．通过对实际高压转子系统的简化处理，考虑到高压转子的温度场较复杂，并非轴对称，建立如图所示的三维实体有限元模型，高压转子的两端简化为弹性支承．

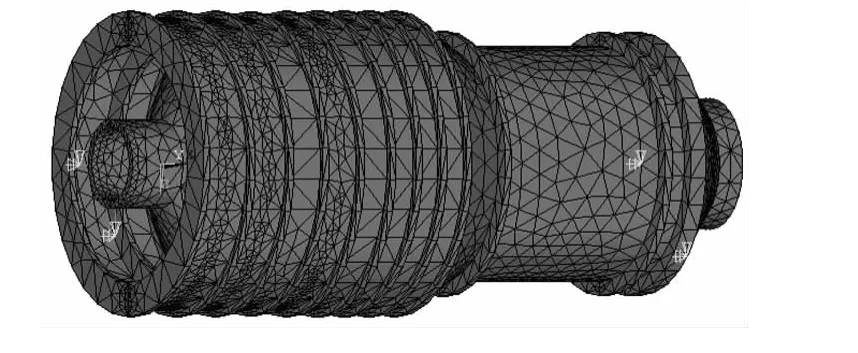
图1 高压转子有限元模型Fig．1 High － pressure rotor FEM model

2．1 稳态温度场对固有频率的影响

2．1．1 弹性模量随温度变化时对固有频率的影响表1为高压转子不同停车时刻，转子的上下温差变化，弹性模量随温度变化时转子前5阶固有频率．可见，随着上下温差的增加、温度升高，转子的弹性模量降低，即转子的刚度降低，各阶固有频率也随之降低．通过图2可以看得到，随着径向温差的增大前两阶固有频率变化幅度相对后三阶变化幅度较小，而且随着上下温差的增大，变化幅度趋于稳定．较高阶的固有频率变化幅度较大，而且其变化幅度有继续增大的趋势，第三阶固有频率的变化幅度最大．

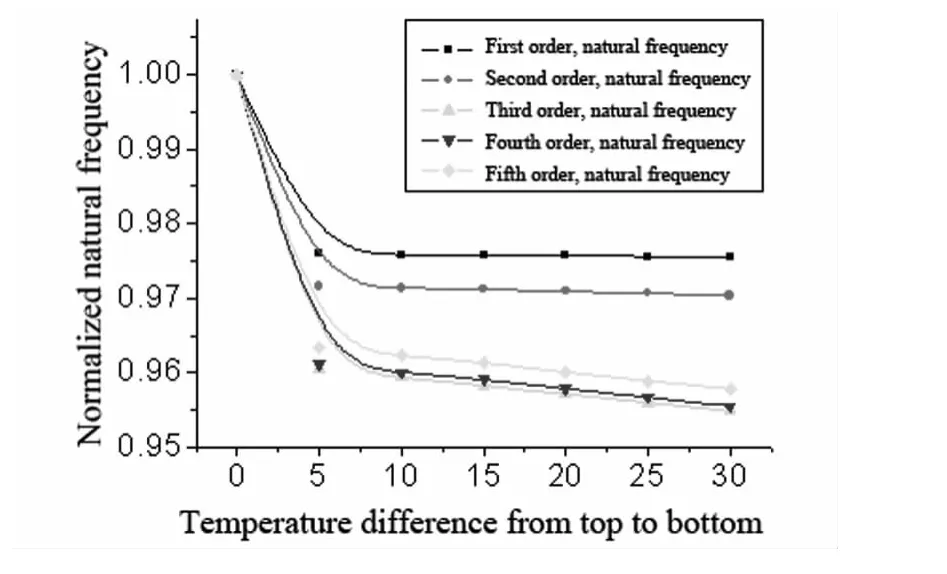
图2 弹性模量变化对固有频率的影响的比较Fig．2 Comparative diagram of the impact on the natural frequency with the change of elasticity module

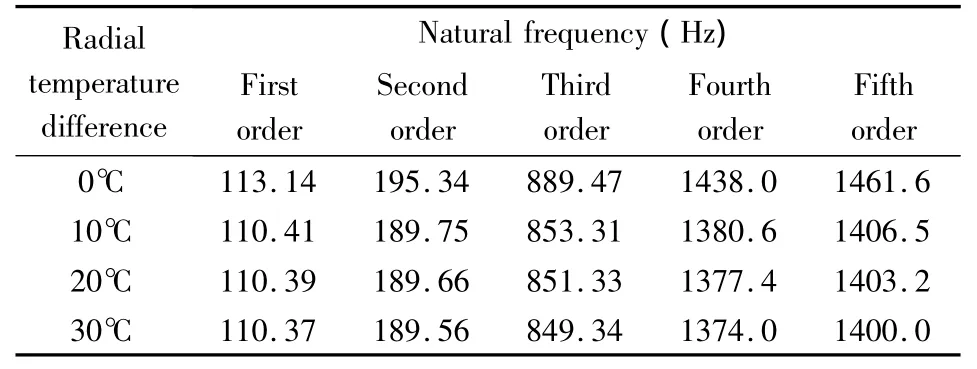
表1 表1弹性模量变化对固有频率的影响Table 1 Effect of elasticity module on the natural frequency

2．1．2 弹性模量和热应力耦合对固有频率的影响

表2为高压转子不同停车时刻，随转子上下温差变化、弹性模量、热应力耦合变化时(简称耦合变化)的前5阶固有频率．可见，由于不均匀膨胀产生的热应力导致了转子系统的刚度变化从而改变转子的固有频率，随着上下温差的增加各阶固有频率均降低．通过图3可以看到，随着上下温差的增大前两阶固有频率变化幅度相对较小，高阶固有频率的变化幅度较大，随着上下温差的增大变化幅度趋于稳定，第四阶固有频率的变化幅度最大，减小了接近20%．显然，弹性模量与热应力耦合变化对固有频率的影响要远大于单纯考虑弹性模量变化对固有频率的影响．

图3 耦合变化对固有频率的影响Fig．3 Effect of coupling variety on the natural frequency

表2 耦合变化对固有频率的影响Table 2 Effect of coupling variety on the natural frequency

2．2 不平衡量和热弯曲耦合响应

2．2．1 热弯曲响应

图4～6为考虑转子转速800rad/s，下边缘温度为200℃，上下温差分别为10℃、20℃、30℃时，二级盘、九级盘、高压涡轮二级盘考虑弹性模量随温度变化时的热弯曲响应．由图可见，由于温度的增加，弹性模量降低，转子变形增大，各阶固有频率对应的响应幅值均增加．由于各阶固有频率减小，导致共振区都相对前移;前三阶模态对热弯曲响应贡献相对较大，尤其是九级盘的第三阶固有频率对应的响应幅值增加幅度较大，同样验证了前面的结论，即第三阶固有频率对弹性模量的变化较为敏感．

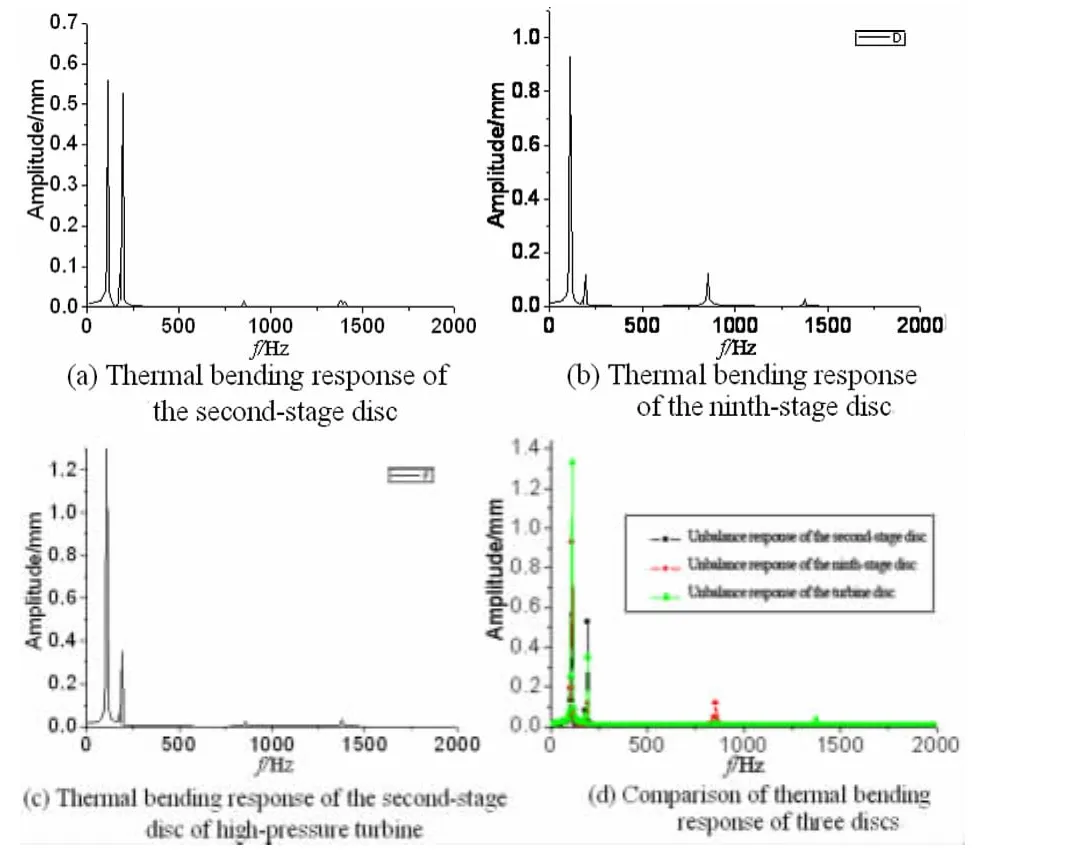
图4 径向温差为10℃，转子热弯响应Fig．4 Thermal bending response of rotor when the radial temperature difference is 10℃

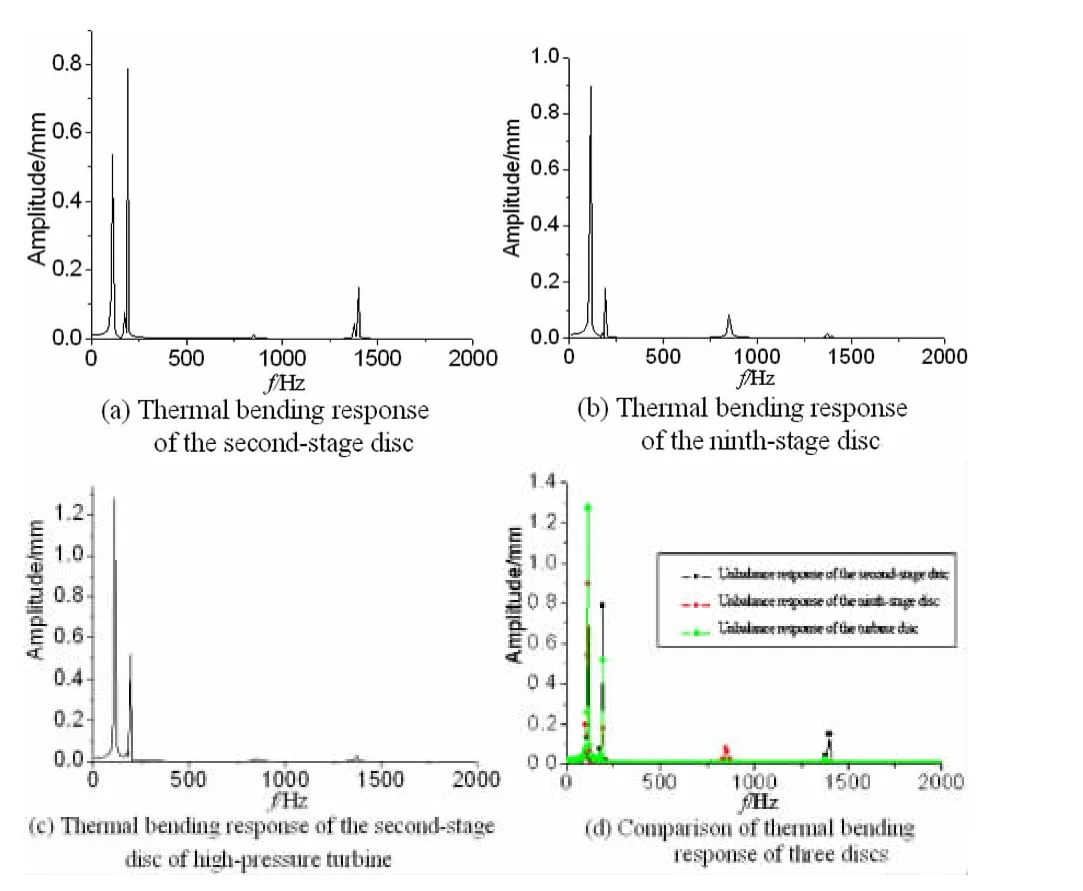
图5 径向温差为20℃，转子热弯响应Fig．5 Thermal bending response of rotor when the radial temperature difference is 20℃

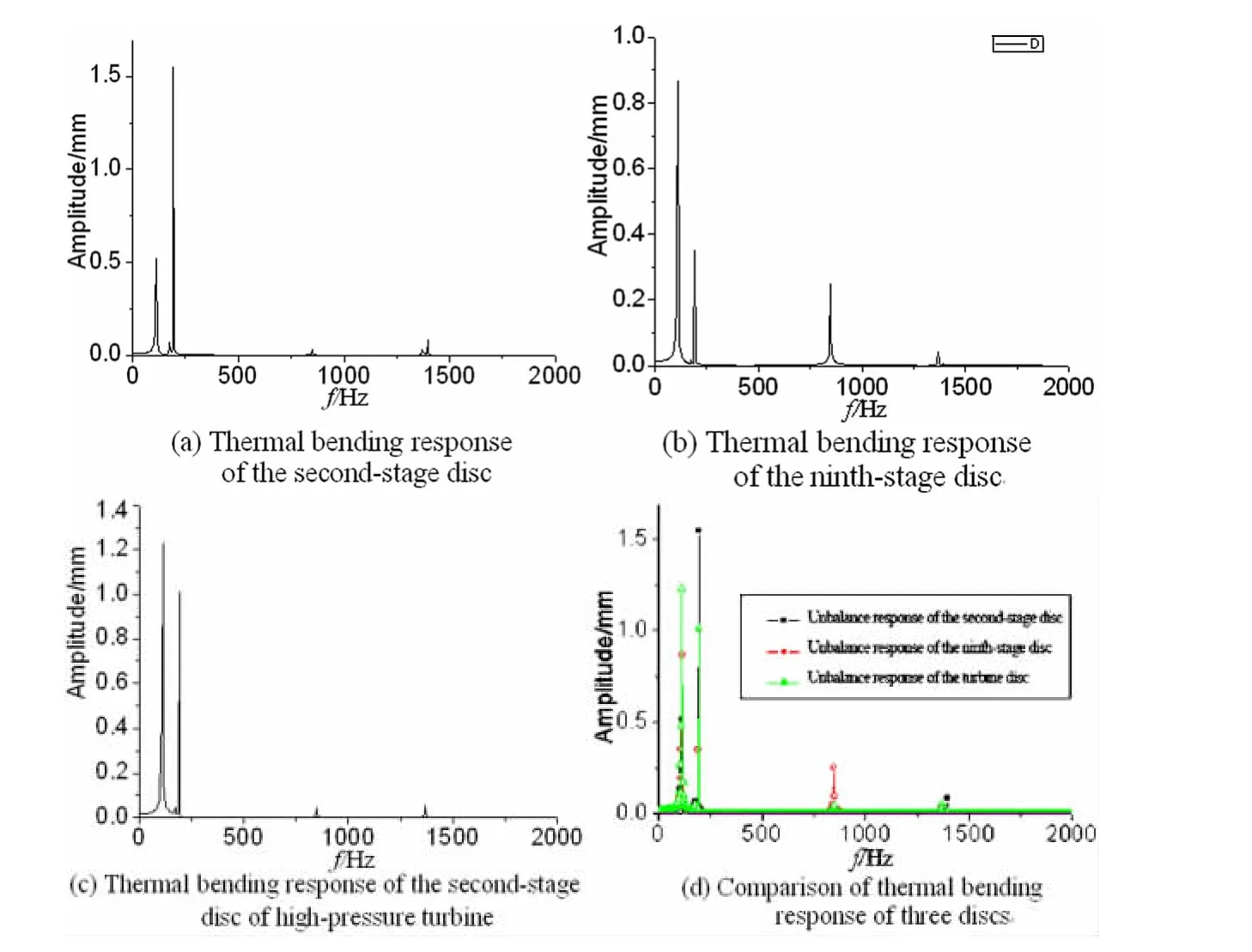
图6 径向温差为30℃，转子热弯响应Fig．6 Thermal bending response of rotor when the radial temperature difference is 30℃

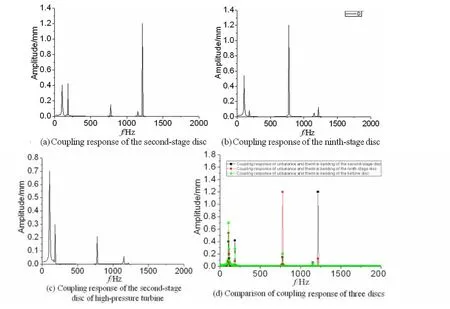
图7 径向温差为10℃时，不平衡量与热弯耦合响应Fig．7 Coupling response of unbalance and thermal bending when the radial temperature difference is 10℃

2．2．2 不平衡量和热弯曲耦合响应

图7～9为考虑转子转速800rad/s，下边缘温度为200℃，九级盘存在不平衡量时，径向温差分别为10℃、20℃、30℃时，二级盘、九级盘、高压涡轮二级盘不平衡量和热弯曲耦合的稳态不平衡响应的幅值谱图．由图可见，各级盘的三、四、五阶固有频率对耦合响应比较敏感．九级盘对三、四阶固有频率最为敏感，其响应幅值远大于不平衡响应和热弯曲响应，它们对耦合响应的贡献要大于一、二阶模态的贡献．涡轮盘二级耦合响应对各阶模态均较敏感，与不平衡响应和热弯曲响应相比三、四阶模态对耦合响应的贡献增大．

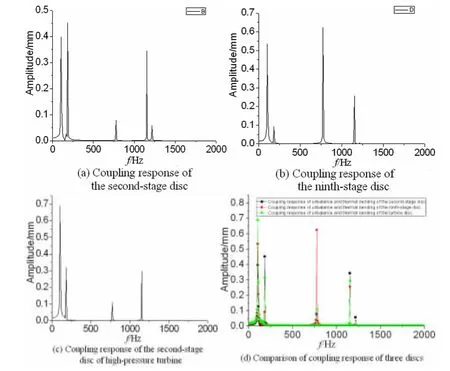
图8 径向温差为20℃时，转子不平衡量与热弯耦合响应Fig．8 Coupling response of unbalance and thermal bending when the radial temperature difference is 20℃

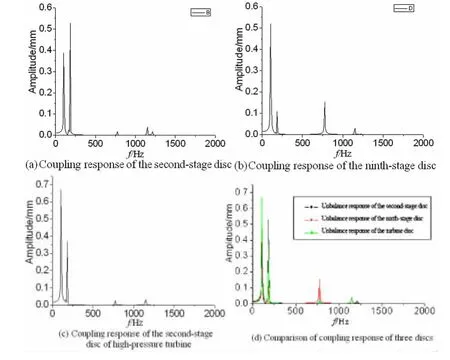
图9 径向温差为30℃时，转子不平衡量与热弯耦合响应Fig．9 Coupling response of unbalance and thermal bending when the radial temperature difference is 30℃

3 结论

研究了某型航空发动机高压转子多种工况下的线性温度分布对高压转子固有频率和不平衡响应的影响，得出了一些具有理论和工程实践指导意义的结论．

1)通过弹性模量变化对固有频率的影响与弹性模量与热应力耦合变化对固有频率的影响的对比，表明弹性模量与热应力耦合变化对固有频率的影响要远大于单纯考虑弹性模量变化对固有频率的影响．可见，在对航空发动机转子系统的振动研究中，必须考虑弹性模量与热应力耦合变化对固有频率的影响．

2)通过不平衡量与热弯曲耦合稳态响应分析发现，耦合响应对转子系统的振动响应有较大影响，且对高阶模态响应较敏感，应尽量避免停车后短时间内迅速启动发动机．

1 郑东亚，丁水汀，杜发荣等．微小型涡喷转子结构热工作稳定性分析及试验验证．航空动力学报，2010，(6):1340～1345(Zheng D Y，Ding S T，Du F R．Analysis and experimental verification of structure－thermal running stability for micro turbojet engine rotor．Journal of Aerospace Power，2010，(6):1340 ～1345(in Chinese))

2 姚学诗，周传荣．转子的热膨胀与横向振动．应用力学学报，2003，20(3):118 ～12(Yao X S，Zhou C R．Thermal expansion and transverse vibration of rotor．Chinese Journal of Applied Mechanics，2003，20(3):118 ～ 12(in Chinese))

3 晏水平，黄树红．汽轮发电机组转子温度分布对其扭转振动的影响．中国电机工程学报，2000，20(11):10～13(Yan S P，and Huang S H．Impact of temperature distribution on the torsional vibration of trubogenerator rotors．Proceedings of the CSEE，2000，20(11):10 ～ 13(in Chinese))

4 贺威，袁惠群．多盘转子系统热启动过程中瞬态响应分析．机械制造，2011，49(3):17～19(He W，Yuan H Q．Analysis of transient response in process of thermal start of multi－disc rotor system ．Machinery，2011，49(3):17 ～19(in Chinese))

5 朱向哲，袁惠群，张连祥．汽轮机转子系统稳态热振动特性的研究．动力工程，2008，28(3):377 ～380(Zhu X Z，Yuan H Q，Zhang L X．Study on characteristics of steady thermal vibration of stream turbine’s rotor system．Power Engineering，2008，28(3):377 ～380(in Chinese))

6 朱向哲，袁惠群，贺威．稳态热度场对转子系统临界转速的影响．振动与冲击，2007，26(12):113～116(Zhu X Z，Yuan H Q，He W．Effect of steady－state thermal field on critical speed of rotor system．Journal of Vibration and Shock，2007，26(12):113～116(in Chinese))

7 Ribeiro P，Manoach E．The effect of temperature on the large amplitude vibrations of curved beams．Journal of Sound and Vibration，2005，285(4/5):1093 ～1107

8 钟一谔，何衍宗，王正等．转子动力学．北京:清华大学出版社，1988(Zhong Y E，He Y Z，Wang Z．Rotor dynam－ic．Beijing:Tsinghua University Press．1988(in Chinese))

9 王士敏．转子通过临界转速时碰摩热效应对振动特性的影响．动力学与控制学报，2004，2(3):64～69(Wang S M．The effect of rub－impact thermal effects on vibration characteristics of a rotor passing through critical speed．Journal of Dynamics and Control，2004，2(3):64 ～ 6 9(in Chinese ))

*The project supported by the National Natural Science Foundation of China(51275081)and Shenyang Science and Technology Plan Projects(F10－205－1－35)

† Corresponding author E－mail:yuan_hq@163．com

ANALYSIS OF THERMAL-STRUCTURAL COUPLING RESPONSE OF 3D SOLID ROTOR SYSTEM*

Li Yan1Yuan Huiqun2†Liang Mingxuan1He Wei3
(1．College of Mechanical Engineering and Automation，Northeastern University，Shenyang110004，China)(2．College of Science，Northeastern University，Shenyang110004，China)(3．College of Higher Vocational Technical，Shenyang Agricultural University，Shenyang110122，China)

With the high－pressure rotor system of an aero－engine as the object of study，in the context of uneven radial distribution of steady－state temperature field，the paper established a FEM model of 3D solid elements of a high－pressure rotor system and vibration equation of thermal－structural coupling model of 3D solid rotor system in the steady－state temperature field．An analysis of the steady－state temperature field was carried out by indirect coupling method using thermal－structural－dynamic coupling theory．Then，A static analysis to generate thermal stress，and global stiffness matrix were performed by setting prestress option to make a modal analysis，Finally，the coupling response of unbalance and thermal bending by modal superposition method were implemented to realize thermal－structural－dynamic coupling computation．Based on the analysis of the effect of steady－state temperature field on steady－state response of typical stage discs and analysis of steady－state response of coupling of unbalance and thermal bending，it can be concluede that the coupling response has a big effect on vibration response of different－stage discs of the rotor system．

three－dimensional solid rotor system， finite element method， natural frequency， steady thermal field， thermal－structural coupling response

26 April 2013，

19 June 2013．

10．6052/1672－6553－2013－091

2013－04－26 收到第 1 稿，2013－06－19 收到修改稿．

*国家自然科学基金(51275081)资助项目，沈阳市科技计划项目(F10－205－1－35)

E－mail:yuan_hq@163．com