分段线性连续系统中的同宿分岔*
2013-09-17徐斌唐云杨凤红林木
徐斌 唐云 杨凤红 林木
(1.清华大学数学科学系,北京 100084)(2.中央财经大学数学系,北京 100084)
分段线性连续系统中的同宿分岔*
徐斌1†唐云1杨凤红2林木2
(1.清华大学数学科学系,北京 100084)(2.中央财经大学数学系,北京 100084)
对于平面上分段线性的连续系统研究了同宿轨的存在性及同宿分岔问题.该系统同宿轨的存在性可以归结为两种情况:一种是由一个可见鞍点和一个可见焦点(或中心)组成的系统;另一种是由两个稳定性相反的结点重合于原点组成的系统.本文对第一种情况给出了同宿轨存在的充要条件,并研究了相应的同宿分岔问题.
分段线性, 同宿轨, 同宿分岔
引言
许多现实际问题都涉及到状态的突然转化,如碰撞、摩擦和电力系统的状态转化等,这类系统需要用非光滑动力系统来描述.因此,虽然对非光滑系统动力学行为研究的历史并不长,近年来却成为一个倍受关注的热门领域.分段光滑系统是非光滑动力系统中的一个重要分支,包括碰撞系统、Filippov系统及连续而不处处可微的向量场系统等[1][2].对线性系统的研究不但非常自然,而且有助于人们理解非线性系统的现象,因而有重要的意义.
本文研究的是平面上的分段线性连续向量场系统,以一条直线为非光滑边界把平面分成两部分,两边的两个半平面内部分别都是线性系统,而且向量场在非光滑边界上是连续的.1998年Freire在[3]中证明了,这样的系统至多只有一个极限环,或孤立的同宿轨,且若极限环存在,则或是吸引的,或是排斥的.这回答了1991年Lum和Chua在[4]提出的问题.对于极限环,Simpson在文献[5]中研究了此类系统中出现的Hopf分岔,随后他又在文献[6]中对极限环问题做了进一步研究.对于有多个非光滑边界的分段线性系统周期轨问题,可以参考文献[7]和[8].在分段线性系统中的分岔现象,可参考文献[9]和[10].
本文对该系统中同宿轨的存在性及同宿分岔问题做了进一步研究.首先将系统变换成规范形式,在给定的规范形式下,同宿轨只能在两种情形下出现:一种是由一个可见鞍点和一个可见焦点(或中心)组成的系统,称为非退化鞍点同宿轨;另一种是由两个稳定性相反的结点重合于原点组成的系统,称为退化鞍点同宿轨.其中后者是平凡的.对于前者,本文给出了同宿轨存在的条件,并研究了其同宿分岔问题.
1 问题概述
本文研究如下的平面线性系统:
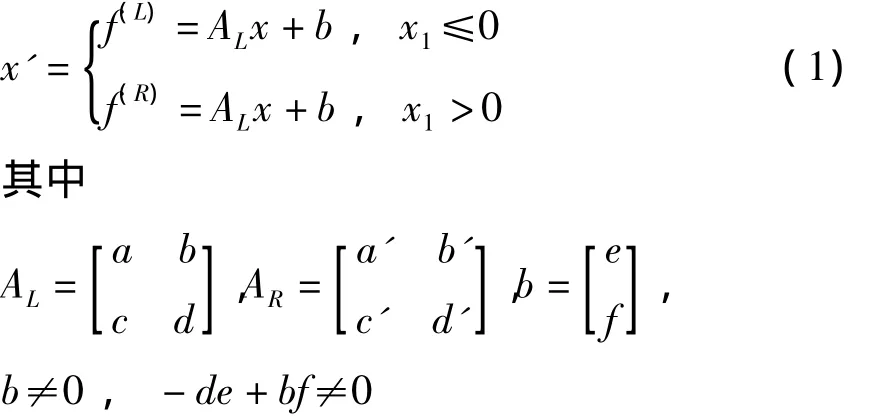
系统以x2轴为非光滑边界.向量场在x2轴上连续.
为了进一步研究,首先要将系统化简,减少参数.做变换:

将系统变成如下的规范形式:


两边的平衡点分别位于

若x*(L)≤0,或x*(R)≥0,则称对应的平衡点是可见的,否则称它是不可见的.
系统(3)的同宿轨可能在两种情况下存在:
1.平衡点不在非光滑边界y轴上,此时平衡点是一个非退化的鞍点.下文称此类同宿轨为非退化鞍点同宿轨.
2.平衡点在y轴上,此时这个平衡点同时是两边的平衡点,是一个退化的鞍点.下文称此类同宿轨为退化鞍点同宿轨.
对于前者,这个平衡点必定是个可见的鞍点.若它在左半平面,则,若它在右半平面,则μ<0.对于后者μ>0,这个平衡点必定位于原点,即μ=0.这种情况是平凡的.下面详细讨论非退化鞍点同宿轨.在这之前,先介绍两个出自文献[3]的引理.
引理1 系统(3)至多存在一个孤立的同宿轨或极限环.若极限环存在,则它或是吸引的,或是排斥的.
引理2 系统(3)存在闭轨线的一个必要条件是 τLτR≤0.
2 非退化鞍点同宿轨的存在性
这一节研究具有非退化鞍点的同宿轨.
不妨设左半平面是个可见的鞍点,即

计算可得AL的特征值和特征向量为


可见鞍点的两个特征方向是一个正向的不稳定流形和一个负向的稳定流形.设它们与y轴交于C1=(0,c1),C2=(0,c2)两点,计算可得
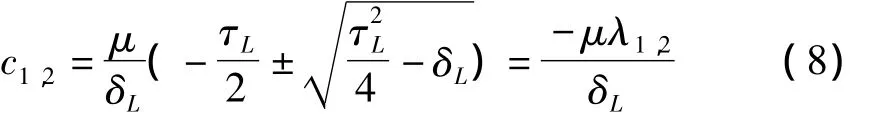
C1在原点上方,C2在原点下方,原点是一个不可见的切点(对于右半平面的系统来说,就是一个可见切点).若同宿轨存在,则必然从鞍点z*(i)出发,沿不稳定流形到达C1,在右半平面被半Poincare映射PR沿顺时针方向映到C2,最后从C2沿稳定流形回到z*(i).如图1所示.
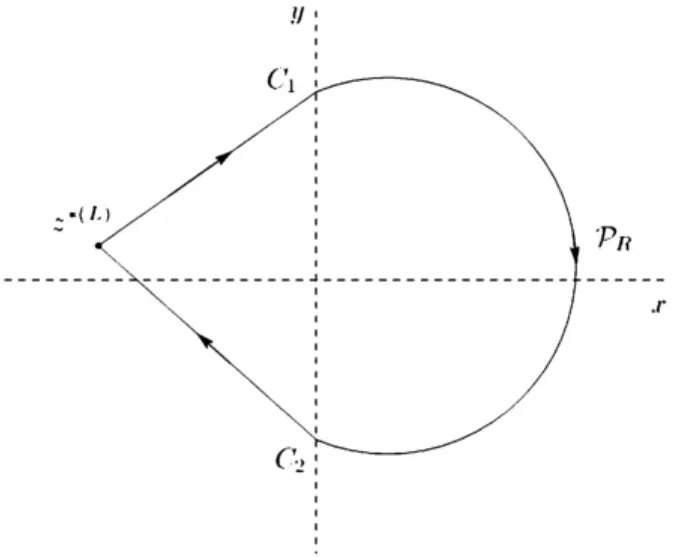
图1 第一类同宿轨的形态Fig.1 homoclinic orbits
根据Poincare-Bendixon定理,同宿轨内部必含一个平衡点,该平衡点为右半平面的可见平衡点.又因为可见的结点和鞍点其不变流形都是直线,轨线不能穿过它们,因此右边系统的平衡点只能是焦点或中心.
同宿轨存在等价于这个焦点将C1映到C2,这是一个很强的条件,若直接解方程,计算量非常之
大,且得到的是一个超越方程,无法求解.所以我们先对系统做一些变换,使得存在条件可以写出来.
记
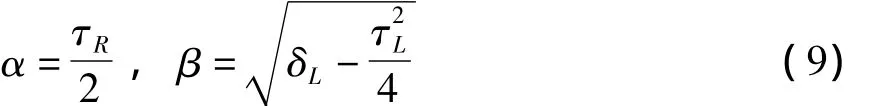
先对右半平面做一个坐标变换:


它将右半平面一一地映到右半平面,因此以下讨论不需要涉及到左边鞍点的部分.
变换之后的系统变成
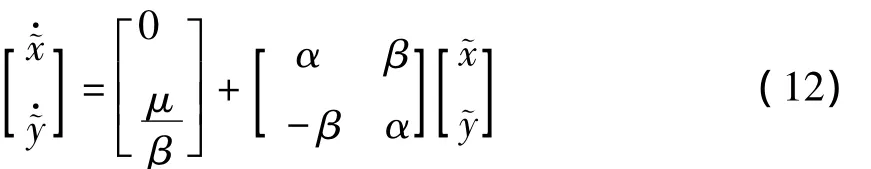
新的焦点位于
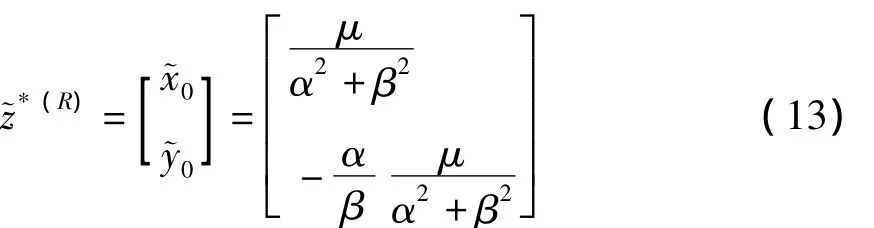
原先的C1,C2两点变成
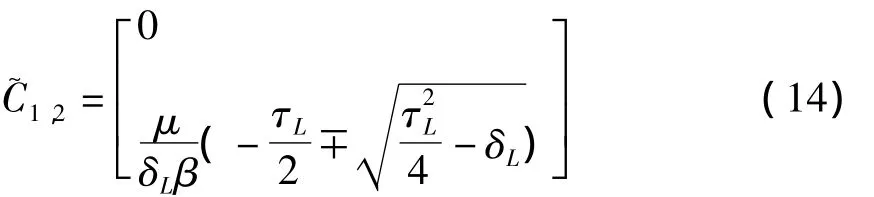
C1仍然在y轴上半轴,在下半轴.变换后的焦点仍沿顺时针方向将映到
将(12)极坐标化:
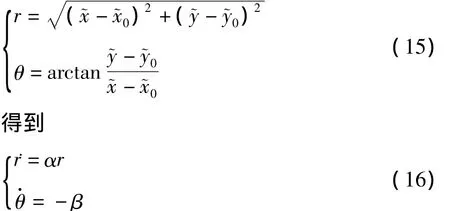
也就是说,在新的坐标下,右边的轨线都是标准的Archimedes螺线:

现记在极坐标下,的坐标为
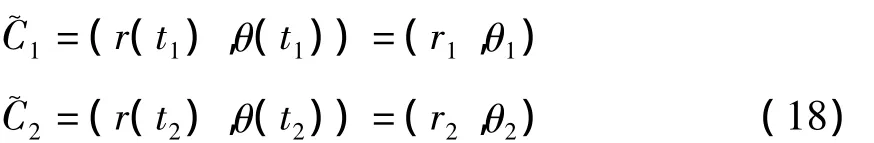
如图2所示.
于是若α≠0,同宿轨存在等价于

注意到上式与μ无关,因此可以直接设μ=1.

图2 坐标变换后的右半平面Fig.2 the right half plane after Coordinate transformation
α=0,即τR=0时,右边为一可见中心,此时的条件需要单独讨论.由于对中心有~c1=~c2,即c1=-c2,得出τL=0.此时同宿轨的存在性与δL无关.该同宿轨内部的轨线都是周期的.
对于μ<0.的情形,同宿轨存在的充要条件与上面的结论相同,但需交换L和R.
整理以上结果,得到下面的结论.
命题1 系统(3)在μ≠0时若存在同宿轨,则是由一边为可见鞍点,另一边为可见焦点或中心的系统组成.
1)若为鞍点和焦点的组合,记鞍点的一边为S,焦点的一边为F(取代原先的L,R),则存在同宿轨的充要条件为满足以下式子:

2)若为鞍点和中心的组合,记鞍点的一边为S,中心的一边为C,则存在同宿轨的充要条件为满足以下式子:
注意到命题1隐含了引理2的结论.
3 非退化鞍点的同宿分岔
这一节将讨论非退化鞍点同宿轨的分岔问题.
仍设左半平面有可见鞍点,根据τL与0的大小关系,同宿分岔可分为两种情况.首先讨论τL≠0的情况.若给系统一个小扰动,使其不满足(21)中的Λ=0,就会发生同宿分岔.根据参数的不同,出现的分岔现象也不同.以下的讨论设μ>0;但对于μ<0的情况,除了P(C1)与C2的关系之外,发生的现象是一样的.
1.当 τF>0时,焦点是排斥的.若 Λ <0,则P(C1)<C2,轨线反向绕向(排斥的)焦点.此时不存在极限环.若Λ>0,则P(C1)>C2,正向绕向一个极限环.引理1保证了这个极限环是吸引的且唯一.
2.当 τF<0时,焦点是吸引的,若 Λ <0,则P(C1)<C2,轨线正向绕向(吸引的)焦点.此时不存在极限环.若Λ>0,则P(C1)>C2,反向绕向一个极限环.引理1保证了这个极限环是排斥的且唯一.
图3(b)是当参数为 μ =1,τL= -0.6333,δL=-0.3667,τR=0.5,δR=2 时存在的同宿轨.图 3(a)(b)(c)分别是当参数 τR=0.4,0.5,0.6 时的分岔现象,τR=0.4时存在一个极限环.
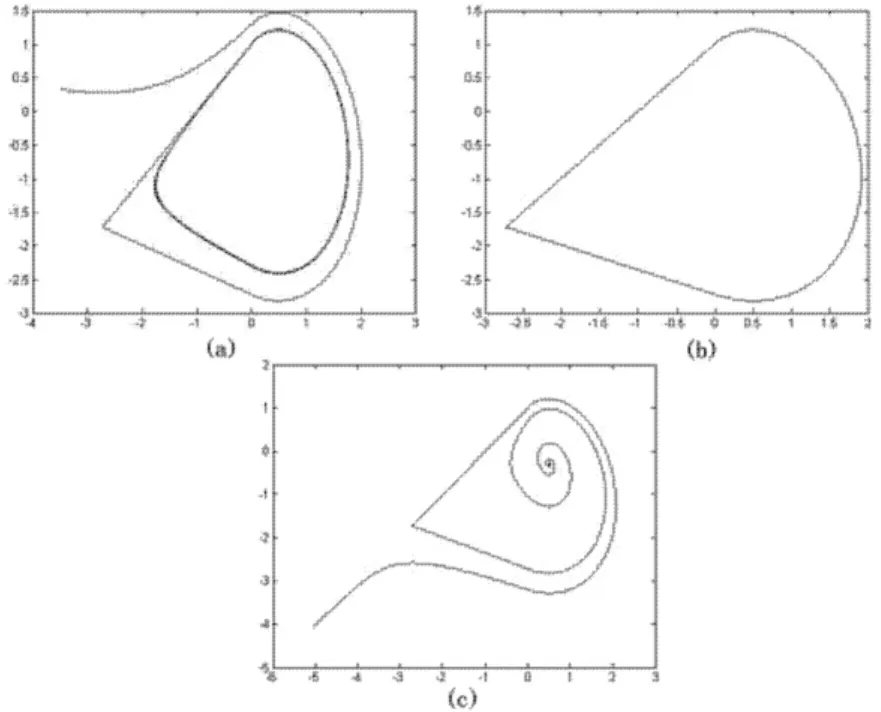
图3 一类分岔现象Fig.3 one kind of homoclinic bifurcations
现在讨论 τR=0 的情况,此时改变 τL,δL,δR都可改变同宿轨的存在性.
(1)若改变 τL,δL而保持 δR不变,则从鞍点出发的轨线或正向或反向绕向一个极限环.引理1保证了这个极限环是存在唯一的,且由中心的性质可知该极限环与原点相切.
(2)若改变 δR而保持 τL,δL不变,则从鞍点出发的轨线或正向或反向绕向可见焦点.引理1保证了此时不存在极限环.
(3)若同时改变 τL,δL,δR,则变为焦点的情形.
图4 是当参数为 μ =1,δL= -1,τR=0,δR=1,τL在0附近时发生的同宿分岔现象.注意到图中有一个半极限环,这种现象在光滑动力系统中非常罕见.
整理上述结论,将μ>0时的分岔现象画在一张图上,见图5.图中的轨线都是沿顺时针方向走的.之所以没有画出τL轴,是因为根据引理2以及命题1,在τR≠0时τL的符号都与之相反,故只需在τR=0时画出特殊情况即可.
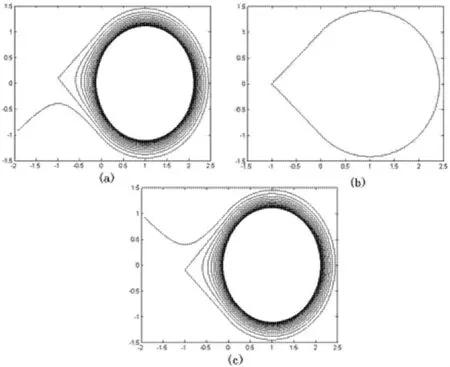
图4 另一类分岔现象Fig.4 another kind of homoclinic bifurcations
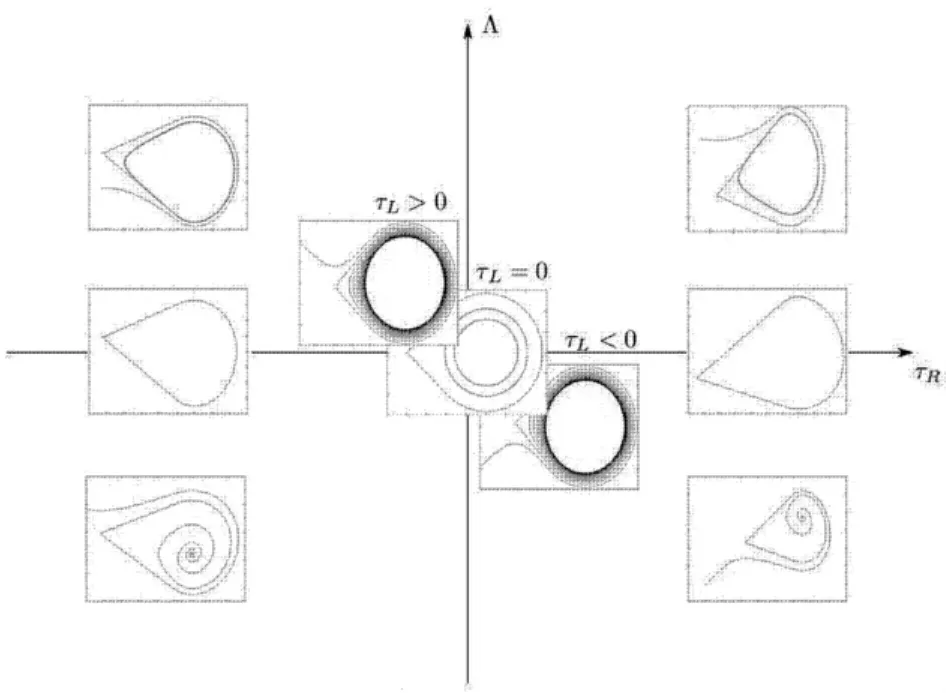
图5 分岔图Fig.5 the bifurcation diagram
从图5可见,描述这个同宿分岔,并不需要全部5个参数,而只需Λ和τR就行了.其中Λ统一了 τL,δL,τR,δR四个参数,用它描述这个同宿分岔更能揭示其本质.
4 结论
至此,系统(3)的所有可能的同宿轨和同宿分岔就研究清楚了.同宿轨只能在两种情况下存在:一个可见鞍点和一个可见焦点(或中心)组成的系统,或者是两个稳定性相反的结点重合于原点的系统,其中后者是平凡的.对前者,第2节命题1给出了这样的同宿轨存在的充要条件.第3节具体研究了该情形下的分岔现象,如图5所示.
1 Di Bernardo M,Budd C J,Champneys A R ,Kowalczyk P.Piecewise-smooth Dynamical Systems Theory and Applications.Springer,2008
2 Di Bernardo M,Pagano D J,Ponce E.Nonhyperbolic boundary equilibrium bifurcations in planar Filippov systems:a case study approach.International Journal of Bifurcations and Chaos,2008,18(5):1377 ~1392
3 Freire E,Ponce E,Rodrigo F,et al.Bifurcation sets of continuous piecewise linear systems with two zones.Int.J.Bifurcation Chaos,1998,8(11):2073 ~2097
4 Lum R,Chua L.Global properties of continuous piecewise linear vector-elds.1.simplest case in R2.Int.J.Circ.Theor.Appl,1991,19(3):251 ~307
5 Simpson D J W,Meiss J D.Andronov-hopf bifurcations in planar,piecewise-smooth,continuous flows.Physics Letters A,2007,371:213~220
6 Simpson D J W.Bifurcations in Piece-wise Continuous Systems.World Scientific,2010
7 Mitrovski C,Kocarev L.Periodic trajectories in piecewiselinear maps.IEEE Trans.Circuits Systems I Fund.Theory Appl,2001,48(10):1244 ~1246
8 Goncalves J M.Regions of stability for limit cycle oscillations in piecewise linear systems.IEEE Trans.Automat.Contr,2005,50(11):1877 ~1882
9 Leine R,Nijmeijer H.Dynamicals and Bifurcations of Nonsmooth Mechanical systems.Springer-Verlag,Berlin,2004
10 Freire E,Ponce E,Rodrigo F,et al.A piecewise linear electronic circuit with a multiplicity of bifurcations.Int.J.Bifurcation Chaos,2004,14(11):3871~3881
*The project supported by the National Natural Science Fundation of China(11072274)
† Corresponding author E-mail:kid0506@163.com
HOMOCLINIC BIFURCATIONS IN PIECEWISE-LINEAR SYSTEMS*
Xu Bin1†Tang Yun1Yang Fenghong2Lin Mu2
(1.Tsinghua University,Department of Mathematical Science,Beijing100084,China)(2.Central University of Finance and Economics,School of Applied Mathematice,Beijing100084,China)
We studied the existence of homoclinic orbits and the homoclinic bifurcations in planar piecewise-linear system.The existence of homoclinic orbit in this system can be divided into two cases,one is a system formed by a visible saddle point and a visible focus(or a center),the other is a system formed by the coincidence of the original point and two nodes with inverse stability.In this paper,we provided the necessary and sufficient condition for the existence of homoclinic orbit,and then analyzed the homoclinic bifurcation.
piecewise-linear, homoclinic orbit, homoclinic bifurcation
19 April 2012,
20 June 2012.
10.6052/1672-6553-2013-005
2012-04-19 收到第 1 稿,2012-06-20 收到修改稿.
*国家自然科学基金资助项目(11072274)
E-mail:kid0506@163.cn
