轴向运动梁横向非线性振动模型研究进展*

丁虎 陈立群 张国策

(1．上海大学，上海市应用数学和力学研究所，上海 200072)(2．上海大学力学系，上海 200444)

轴向运动梁横向非线性振动模型研究进展*

丁虎1†陈立群1，2张国策1

(1．上海大学，上海市应用数学和力学研究所，上海 200072)(2．上海大学力学系，上海 200444)

综述了描述轴向运动梁横向非线性振动的两组数学模型的研究进展．在轴向运动梁径向和横向平面非线性振动耦合模型的基础上，总结了两组横向非线性振动模型的推导，以及在自由振动、受迫振动、参激振动工况下两组横向模型的近似解析比较的研究进展．在直接数值离散方法的基础上，总结了两组横向模型在各种工况下对平面耦合模型近似程度的研究进展．最后提出若干尚待深入研究的问题．

轴向运动梁， 振动， 非线性模型， 解析分析， 数值仿真

引言

现实生活中的多种工程系统元件，如动力传送带、带锯、空中缆车索道、高楼升降机缆绳、汽车中驱动带等，均可以模型化为轴向运动连续体［1－3］．计及抗弯刚度时，即可以轴向运动梁为模型．物理模型如图1所示．

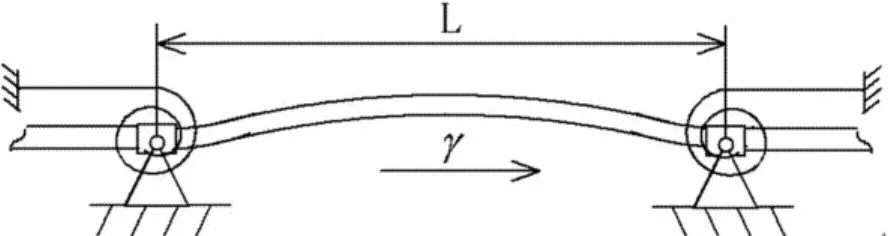
图1 轴向运动梁物理模型Fig．1 The physical model of an axially moving beam

在不计及抗弯刚度的条件下，1966 年，Mote［4］应用Hamilton原理，并假设径向位移的空间导数很小并予以忽略的假设条件下，首先发展了轴向运动弦线横向非线性振动控制方程，一个非线性偏微分方程．Chen等［5－7］综述了相关研究进展．计入抗弯刚度，该模型能够拓展为描述轴向运动梁横向非线性振动的模型，并在轴向运动梁横向振动问题的研究中有着广泛的应用．运用该非线性偏微分方程，Pakdemirli课题组分别研究了轴向运动梁非线性参数振动稳定性［8］和受迫振动主共振响应［9］以及受迫振动3:1内共振响应［10］，Marynowski课题组分别应用不同的黏性阻尼研究了黏弹性轴向运动梁的非线性动力学行为［11，12］，陈树辉课题组分别通过谐波平衡法［13，14］和 Lindstedt－ Poincaré方法［15，16］研究了有无内共振时轴向运动梁的非线性振动，Zhang课题组通过Hamilton原理推导出该黏弹性非线性偏微分方程［17］，并分别研究了有无内共振时轴向运动梁的非线性动力学［18－20］，李映辉等［21］通过 Galerkin 截断分析了参数振动的横向振动响应，Ghayesh等［22－25］分别通过轴向运动弦线、Euler梁和Rayleigh梁模型研究了非线性参数振动的稳态响应，Chen课题组通过近似解析方法研究了轴向运动梁的非线性参数振动［26］以及受迫振动［27］．

1969 年，Thurman 和 Mote［28］应用 Hamilton 原理，并考虑线性弹性和几何非线性时，首先发展了轴向运动梁平面耦合非线性振动的控制方程．对于小而有限的伸展问题，在准静态假设下，1992年，Wickert［29］将 Thurman 和 Mote 的耦合模型解耦，得到轴向运动梁横向振动的另一个控制方程，一个非线性偏微分—积分方程．该模型也同样广泛应用于轴向运动梁的非线性横向振动研究中．基于非线性偏微分—积分方程，Ravindra和 Zhu［30］研究了超临界非线性动力学行为，Pellicano课题组分别研究了轴向运动梁的弱非线性振动［31］，非线性动力学及分岔［32］和超临界运动状态下的非线性动力学［33］，Chakraborty等分别研究了参数激励［34］和集中力激励［35］的轴向运动梁横向非线性振动，Parker和Lin［36］研究了多频张力和速度脉动激励下的非线性参数振动响应，Chen课题组分别研究了轴向运动梁横向非线性自由振动［37］和受迫振动［38］的响应，以及轴向运动弦线横向非线性参数共振［39］的混沌性态．

通过略去耦合方程中的径向量以及关于横向量的高阶非线性项，也能够从平面运动模型得到描述轴向运动梁横向振动的非线性偏微分模型．比较Wickert［29］推导非线性偏微分—积分模型的过程，有理由相信非线性偏微分—积分模型更加精确．因为两个横向振动模型都能够从平面耦合模型直接推导得出，但是在非线性偏微分模型的推导过程中，是直接令径向位移为零并略去高阶非线性项，而在非线性偏微分—积分模型的推导中是考虑了径向位移的，尽管最后实现了完全解耦．另一个方面，Chen和Yang［40］通过准静态假设直接从非线性偏微分模型推导出非线性偏微分—积分模型，因此，看起来非线性偏微分—积分模型应该是非线性偏微分模型的一种近似模型．综合两组横向模型的推导过程能够得出以下结论，即对于以上两组轴向运动梁横向非线性振动研究中常用的数学模型，仅从推导过程的角度做判断，是不能确定哪个模型是更加有效、更加适用的．

本文将综述轴向运动梁两组横向非线性振动模型比较的研究进展．对于两组非线性模型的比较分为两类，其一是两组模型间定量差别的比较，即通过近似解析方法比较不同工况下两组模型的响应;其二是与耦合模型横向分量的比较，即通过数值方法比较不同工况下两组模型的响应与平面耦合非线性模型响应的横向分量，从更加接近耦合模型横向分量的角度，评定两组横向模型中哪个更有效、哪个更加适用于描述轴向运动梁在不同工况的运动状态．本文的综述从这两个方面展开．

1 两种横向运动的非线性模型

考虑截面积为A、密度为ρ、初始张力为P0的梁以一致的速度沿轴向运动，其速度为γ，梁弹性模量为E．只考虑梁横向和径向变形，在径向空间坐标x处，t时刻横向位移为v(x，t)，轴向位移为u(x，t)，由于运动产生的扰动应力为σ，外载荷的轴向和横向分量依次为fu(x，t)和fv(x，t)．对于细长的梁，径向与横向耦合运动的非线性动力学控制方程为［13，28］

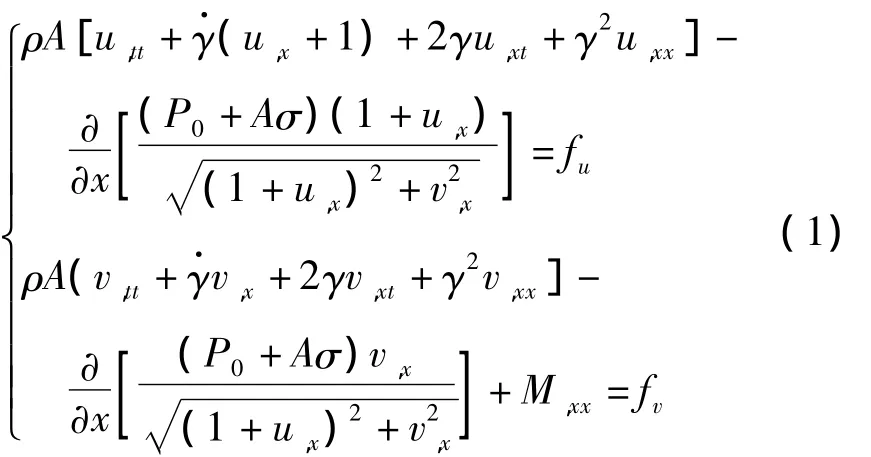
式中，逗号后的x和t分别表示对x和t的偏微分，其中M=M(x，t)为梁在轴向坐标x和时间t的弯矩，对于给定的梁模型和材料，弯矩可以用横向位移表示，例如，细长梁可以采用Euler－Bernoulli梁模型，若梁的黏弹性属性由取物质导数的Kevlin本构关系描述，则扰动应力和弯矩－位移关系分别为

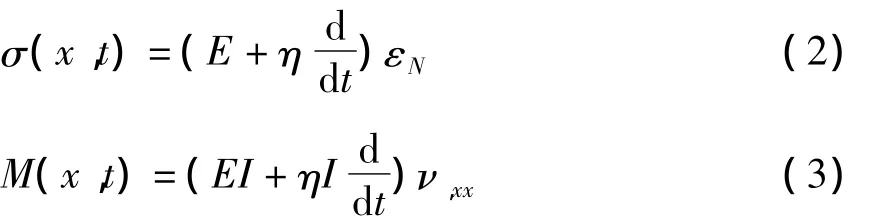
其中η为梁的黏性系数，I为梁的截面二次矩．相应的应变－位移关系为

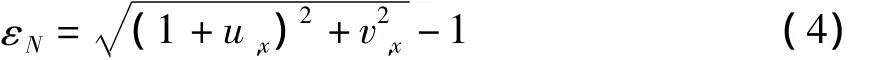
若忽略耦合效应而仅考虑横向运动，即在式(1)中插入u=0，并忽略高阶非线性项，得到

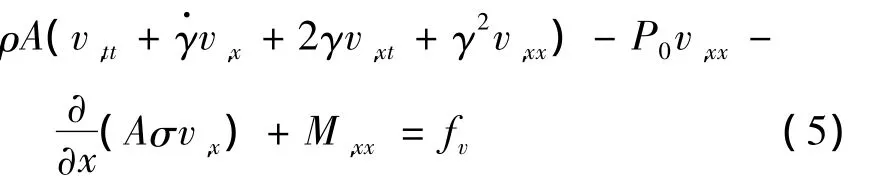
式(5)就是轴向运动梁横向振动非线性偏微分模型．相应地，式(4)退化为所谓Lagrange应变

梁的另一类数学模型，即非线性偏微分－积分模型可以在式(5)中取平均扰动应力得到，即

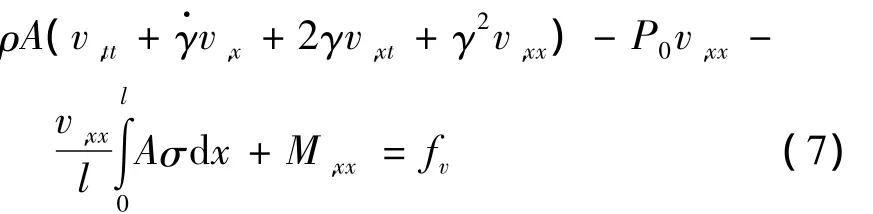
将式(4)或者式(6)代入式(2)，并将结果分别代入式(1)、(5)和(7)，就能够得到三组常用于轴向运动梁非线性振动研究的模型．若方程中部分系数取零，就能够得到不同工况下梁振动控制方程，例如，若不受外载荷作用且轴向速度和初始张力均为常数，梁的横向运动为自由振动;若受周期性外载荷作用且轴向速度和初始张力均为常数，梁的横向运动为简谐受迫振动;若不受外力作用但初始张力有周期性变化，梁的横向运动为参数振动．

2 两种横向非线性模型的定量差别

随着两组横向振动非线性模型在轴向运动梁横向运动研究中的广泛应用，两组模型的差别也逐渐引起关注．

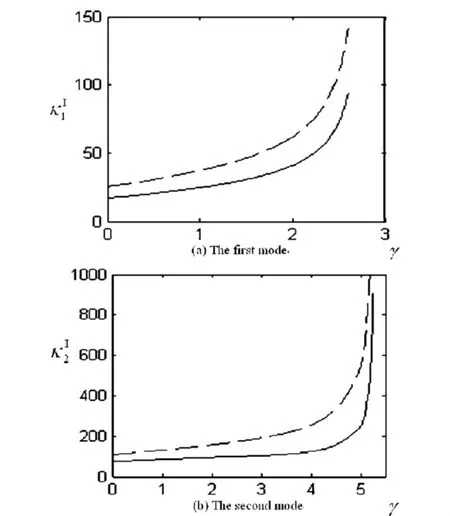
图2 两模型非线性项对横向振动频率的影响随轴向速度的变化Fig．2 Effects of nonlinearity on two transversal frequencies versus the axial speed

2007 年，Chen 和 Yang［41］通过近似解析方法比较了两端简支边界条件下，两组横向非线性模型描述的轴向运动梁对初始激励响应的横向自由振动频率．研究结果表明，当非线性较弱、轴向运动速度较小或对于较低阶模态时，两种横向非线性模型的计算结果相差不显著;随着初始振动幅度的增大，两种横向非线性模型计算的固有频率受到非线性系数的影响也会增大;当轴向运动速度增大时，两种模型受非线性系数的影响也会随着增大，尤其当速度接近临界速度时;对于较高阶的模态，两种模型受非线性系数的影响也相对较大．如图2给出了表示非线性项对自由振动频率影响的参数随轴向运动速度γ的变化情况．图中虚线和实线分别表示非线性偏微分模型和非线性偏微分-积分模型得到的结果．如图所示，表示偏微分非线性项影响的参数比偏微分-积分大，尤其是当轴向速度增大时，这二者差别就会更加明显．研究结果表明，沿梁的轴向对应力积分，从而取应力平均值取代梁上各点的应力值，使得控制方程的非线性属性减弱．但是图中所示的两者随轴向运动的变化趋势完全一致．

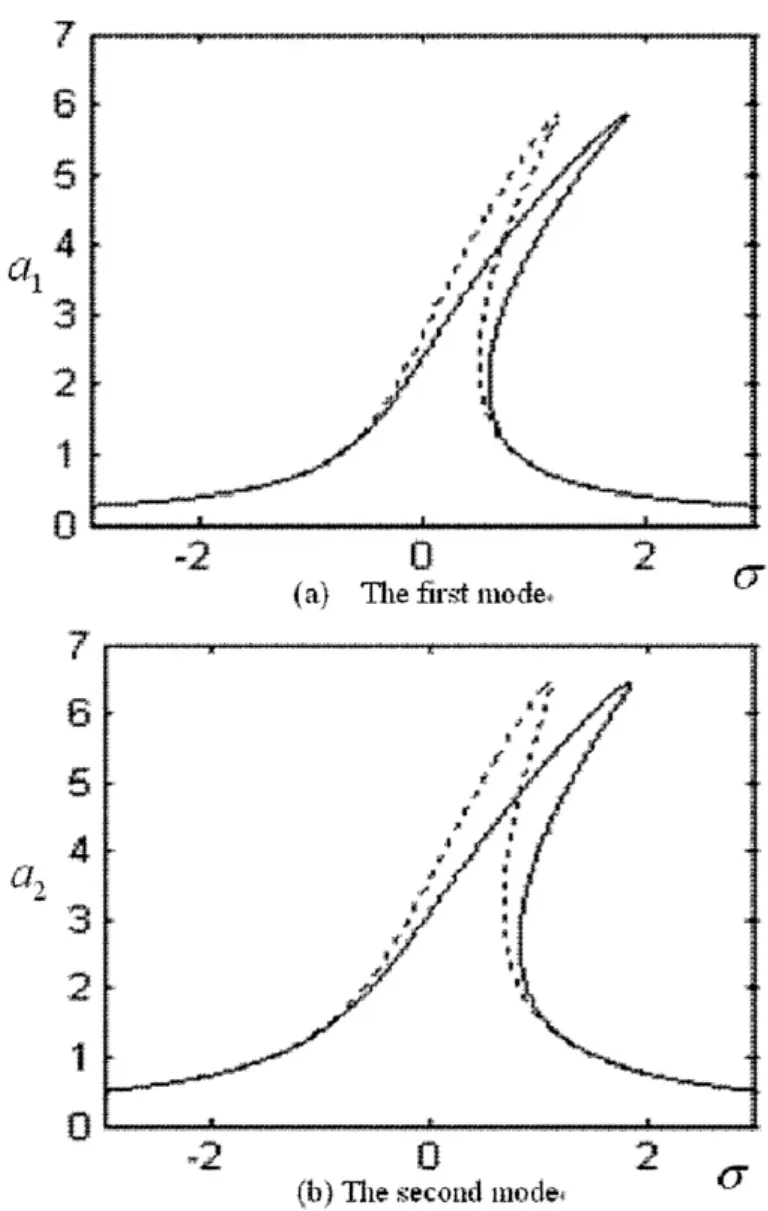
图3 两组非线性模型横向受迫幅频响应曲线的比较Fig．3 Comparison between the frequency － response curves from two transversal models

2006 年，Yang 和 Chen［42］通过直接多尺度方法比较了两端简支边界条件下轴向运动梁的两组横向模型在受简谐外激励下的横向响应振幅．研究表明，远离共振时，两组横向非线性振动模型的数值结果无明显差别，但是在前两阶模态的共振区域，两组模型间差别明显．如图3给出了非线性偏微分模型及非线性偏微分—积分模型在相同参数下的稳态响应振幅随外激励频率变化曲线的比较，图中横坐标为解谐参数，表示外激励频率离开轴向运动梁各阶未扰系统固有频率的距离，纵坐标表示稳态响应振幅．图中实线表示非线性偏微分模型，虚线表示非线性偏微分—积分模型．从图中可以明显看出，代表非线性偏微分模型的实线向右弯的幅度更大，说明偏微分模型的非线性属性要比偏微分—积分模型强．

Chen和Yang［40］通过近似解析方法比较了两端固定的边界条件下，两组横向模型描述的受轴向速度脉动激励的横向响应．研究表明，两组非线性横向振动模型描述的轴向运动梁在参激振动中的失稳区域是完全一致的，但是积分非线性项要比偏微分非线性项较弱，这是因为认为梁的轴向应力沿轴向不做变化的准静态假设减弱了非线性项的影响．如图4显示，虚线表示非线性偏微分—积分模型结果，实线表示非线性偏微分模型结果．图中横坐标为解谐参数，表示外激励频率离开轴向运动梁某一阶未受扰动系统固有频率二倍的距离．比较图中曲线容易发现，代表非线性偏微分—积分模型的虚线向右弯曲的幅度较小，因此偏微分—积分模型的非线性属性较弱．

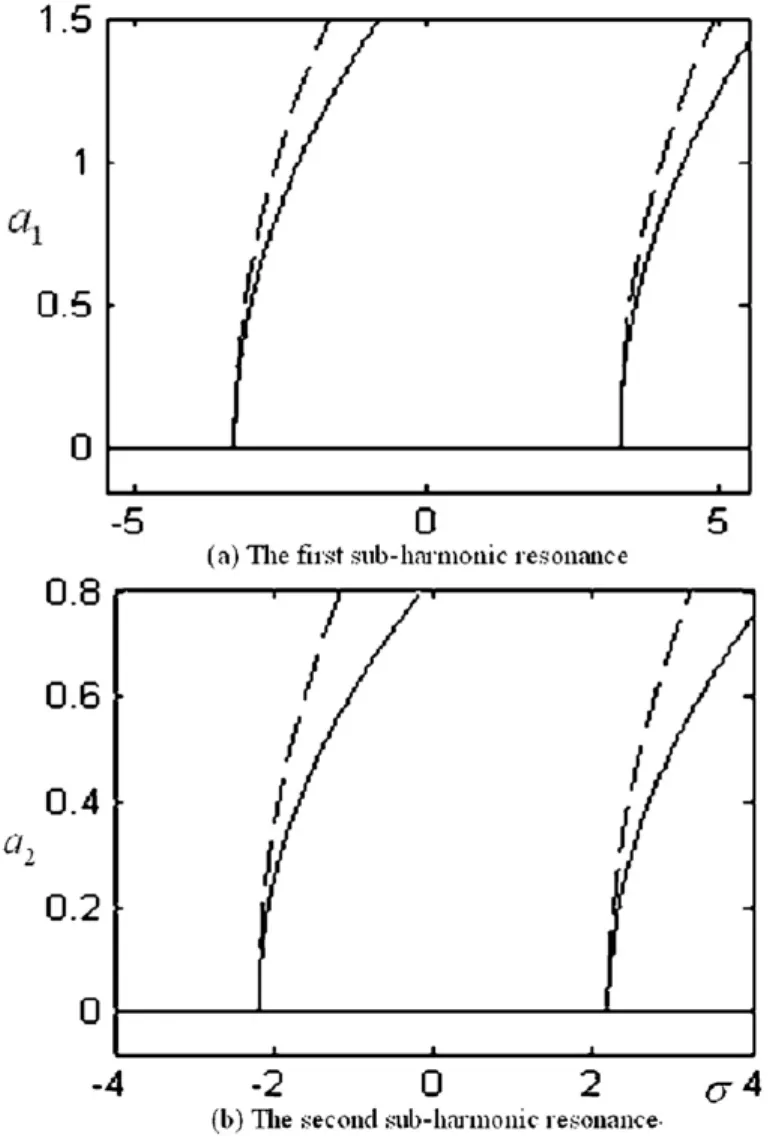
图4 两组非线性模型次谐波共振响应曲线的比较Fig．4 Comparison between the sub － harmonic resonances from two transversal models

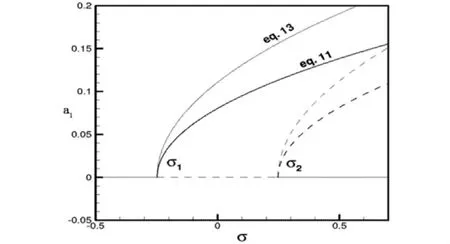
图5 两组Timoshenko梁横向模型次谐波共振响应曲线的比较Fig．5 Comparison between the sub － harmonic resonances from two Timoshenko beam＇s models

计入绕梁中性轴的转动惯量以及剪切变形的影响，描述梁横向振动的两组非线性模型能够扩展成更加复杂，同时也更为精确的Timoshenko梁模型．2010 年，Ghayesh等［43］通过 Timoshenko梁模型比较了两组横向非线性振动模型对因轴向运动周期变化引起的参数激励响应的描述．研究结果显示，对于复杂的梁模型，两组横向振动非线性控制方程在定量上的差别和Euler－Bernoulli梁模型一致．如图5所示，图中的eq．11响应曲线表示非线性偏微分模型结果，eq．13响应曲线表示非线性偏微分—积分模型结果．

通过直接数值方法离散两组横向模型，Ding和Chen［44］验证了此前近似解析方法在外部激励工况下对两组模型的比较结果，Chen和Ding［45］验证了多尺度方法分析在轴向速度扰动激励工况下对两组模型的比较结果．Chen等［46－48］还通过近似解析方法比较了不考虑抗弯刚度时，由式(5)和(7)中退化得到的两组轴向运动弦线横向非线性振动模型，在参数激励下的稳态响应，得到的结论和两组梁横向振动模型比较的结论基本相同．

综合上述，在一系列近似解析方法对轴向运动连续梁或者弦线两组横向非线性振动模型的比较中，虽然所处的工况不同，但是却有着相似的结论，即在定性分析上，两组横向模型呈现相同的趋势，而在定量比较上，两组模型又表现出明显的不同．就非线性属性而言，非线性偏微分模型比非线性偏微分—积分模型强，可见，沿着梁的轴向对应力积分而取平均值，使得非线性性质减弱．考虑到这两组横向振动的模型在轴向运动连续体研究中的广泛应用，定量上的不同，就提出一个亟待解决的问题，即哪一组模型更加有效、更加适用?

3 与耦合模型的横向分量比较

以上对于两组横向非线性振动模型的比较，确定了模型间存在定量上的区别，却没有给出相对于不同的运动状态时，两组模型中哪个更有效、更适用的判定．

Ding和Chen［49］通过直接数值方法比较两组横向非线性模型对自由振动响应与平面耦合非线性模型横向分量的比较，以判定哪个模型更加接近耦合模型的横向分量，并以此为标准，判定两组横向模型的有效性．经过数值算例的对比，发现当初始振幅较小时，短时间内，横向偏微分模型和偏微分－积分模型对耦合模型横向分量的近似效果都非常好;随着初始横向位移幅度的增大，横向偏微分模型和偏微分－积分模型随时间的响应历程均开始偏离耦合模型，但是相比较而言，横向偏微分－积分模型更加接近耦合模型的横向分量;即使在初始横向位移幅度很小的时候，在经历一段较长的时间以后，横向偏微分模型和偏微分－积分模型的时间响应历程均开始偏离耦合模型的横向分量，而横向偏微分－积分模型的时程始终更为接近耦合模型的横向分量．如图6给出了受初始位移激励时，两组横向非线性振动模型描述的轴向运动铜材料梁中点对初始位移的动态响应与耦合模型横向分量间的对比．图6以及本文接下来对比两组横向模型与平面耦合模型横向分量的图中，点均代表对应平面耦合模型，实线代表对应非线性偏微分－积分模型，虚线代表对应非线性偏微分模型．从图6中可以清楚看出，轴向运动梁的横向偏微分－积分模型要比横向偏微分模型在时程上更加接近轴向和横向耦合模型的横向分量．

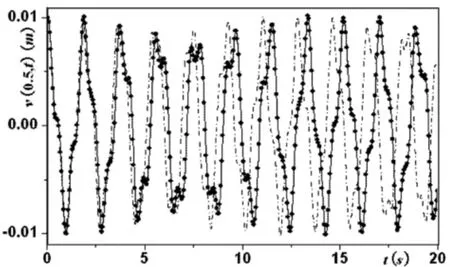
图6 铜材料梁中点的初始响应比较Fig．6 Comparison on the initial responses at the midpoint of a copper beam

Ding和Chen还通过定义类方差的统计指标，提出将梁上的各个离散点随时间变化的数值解作为比较依据，定量的比较了轴向运动梁两组横向自由振动非线性模型与平面耦合模型横向分量．如表1所示，表中的Al表示连续体初始位移的幅度，类方差指标和分别表示横向非线性偏微分模型和横向非线性偏微分－积分模型对耦合模型横向分量在整个计算时间范围内的近似程度．观察表1能够从定量上清楚的发现，两组横向模型与耦合模型横向分量间的差别均随初始位移幅值的增大而增大，而且非线性偏微分—积分模型与耦合模型横向分量间的差别始终相对较小．

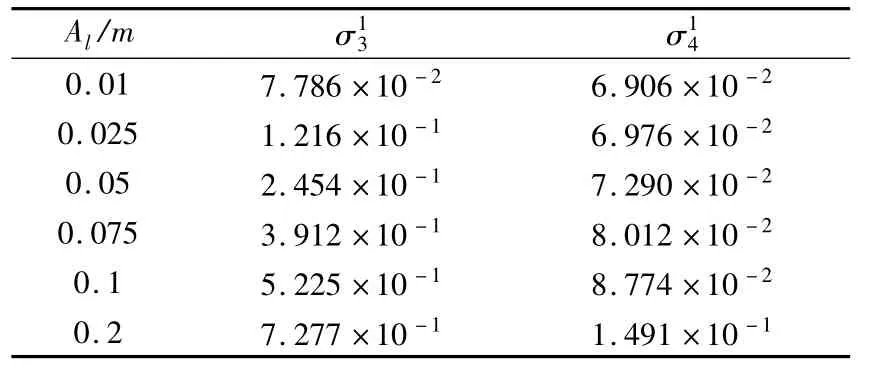
表1 轴向运动钢材料梁的非线性横向模型比较Table 1 The deviations of the two transversal models for an axially moving steel beam

Chen和Ding［50］还通过随时间的响应历程以及类方差的统计指标，定量的比较了静态弦线两组横向自由振动非线性模型与平面耦合模型横向分量，得到和以上轴向运动梁文献中相似的结论．如表2所示，从统计指标可以定量的看出，相比较于轴向运动梁，运动弦线的两组横向非线性模型都更加接近耦合模型的横向分量，钢弦线算例中非线性偏微分－积分模型要比非线性偏微分模型更加接近耦合模型的横向分量的程度，如表中所列数据，此结论还不仅仅局限于微幅振动，对于大幅度的横向振动，也同样适用．

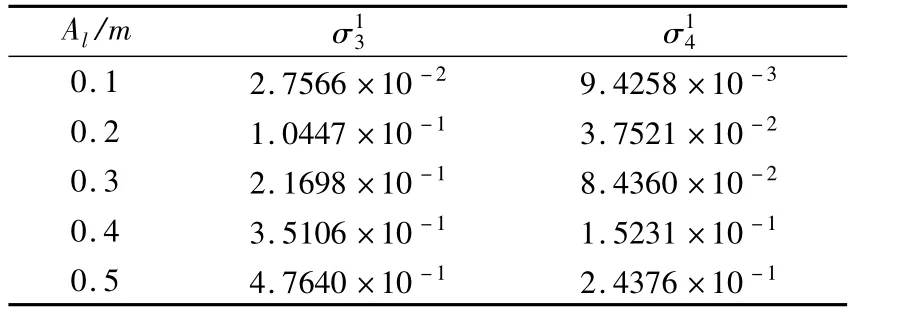
表2 静态橡胶材料弦线的非线性横向模型比较Table 2 The deviations of the two transversal models for a rubber string

Chen 和 Ding［51，52］通过直接数值方法比较了不同边界条件下两组横向模型的受迫振动响应以及稳态响应时梁的形状与平面耦合模型横向分量的比较，判定两组横向模型在外部简谐激励时的有效性．通过算例比较发现，无论两端简支还是固定，横向偏微分模型向右弯曲的幅度总是最大，也就是说三组模型中的横向偏微分模型的非线性属性最强，在数值试验能够取到的参数值的范围内，轴向和横向耦合的模型的横向分量与偏微分－积分模型的受迫共振稳态幅频曲线以及梁的形状总是吻合的很好;通过比较外激励频率取未受扰动系统固有频率时的受迫振动稳态下的对应于三组模型的梁的形状，发现对应于横向偏微分模型的梁的振动幅值总是最小的，轴向和横向耦合的模型与偏微分－积分模型的受迫共振稳态时梁的形状总是吻合的很好．

如图7和8所示，分别给出了两端简支边界和两端固定边界下轴向运动黏弹性梁横向受迫振动工况下，两组横向非线性振动模型的横向响应与平面耦合模型横向分量响应的对比．图中清楚的显示，存在周期性外激励时，从时间响应历程上看，轴向运动梁的横向非线性偏微分－积分模型始终与轴向和横向耦合模型的横向分量吻合;暂态过程图7(a)显示，横向非线性偏微分模型在振幅和相角上与耦合模型都存在较大差别，但是进入稳态阶段图7(b)后，除了振动幅度有细微差别以外，与耦合模型也吻合的较好;从外激励频率与稳态响应振幅的关系曲线图(8)可以看出，非线性偏微分－积分模型都要比横向偏微分模型在非线性受迫振动的稳态幅频响应上更加接近轴向和横向耦合模型的横向分量．

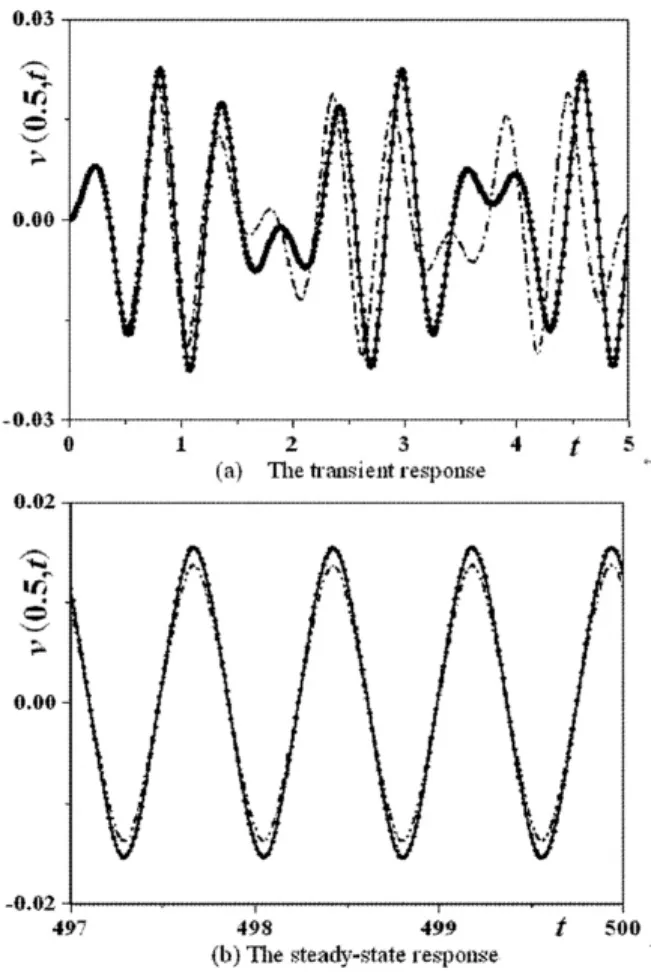
图7 梁中点的受迫振动时间响应历程比较Fig．7 Comparison on the time histories at the midpoint of an axially moving beam

Ding和Chen［53］还通过直接数值方法结合快速Fourier变换比较了两组模型描述的轴向运动梁非线性振动频率与平面耦合振动横向部分的运动频率．研究表明，随着非线性系数和初始振幅的增大，两组横向非线性模型对应的自由振动梁的前两阶固有频率和平面耦合振动频率有着相同的变化趋势，而且非线性偏微分－积分模型和非线性耦合模型基本吻合，但是对应非线性偏微分方程的前两阶固有频率和耦合模型对应频率的差别逐渐增大;在振动幅度和非线性系数不大的情况下，随着弯曲刚度和轴向速度的增大，两组横向非线性模型对应的自由振动梁的前两阶固有频率和平面耦合运动横向部分的频率有着相同的变化趋势，而且对应于不同非线性模型的固有频率基本重合，没有明显差别．

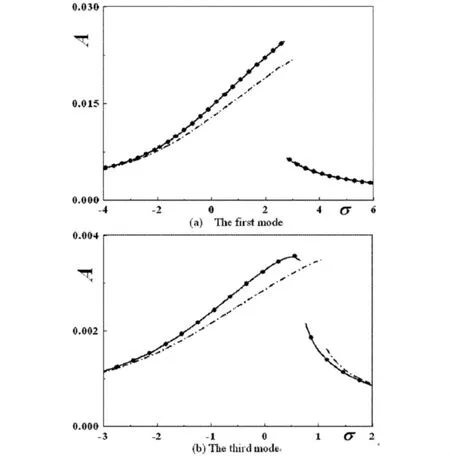
图8 梁中点的受迫振动稳态响应的比较Fig．8 Comparison on the frequency － response curves at the midpoint of the moving beam

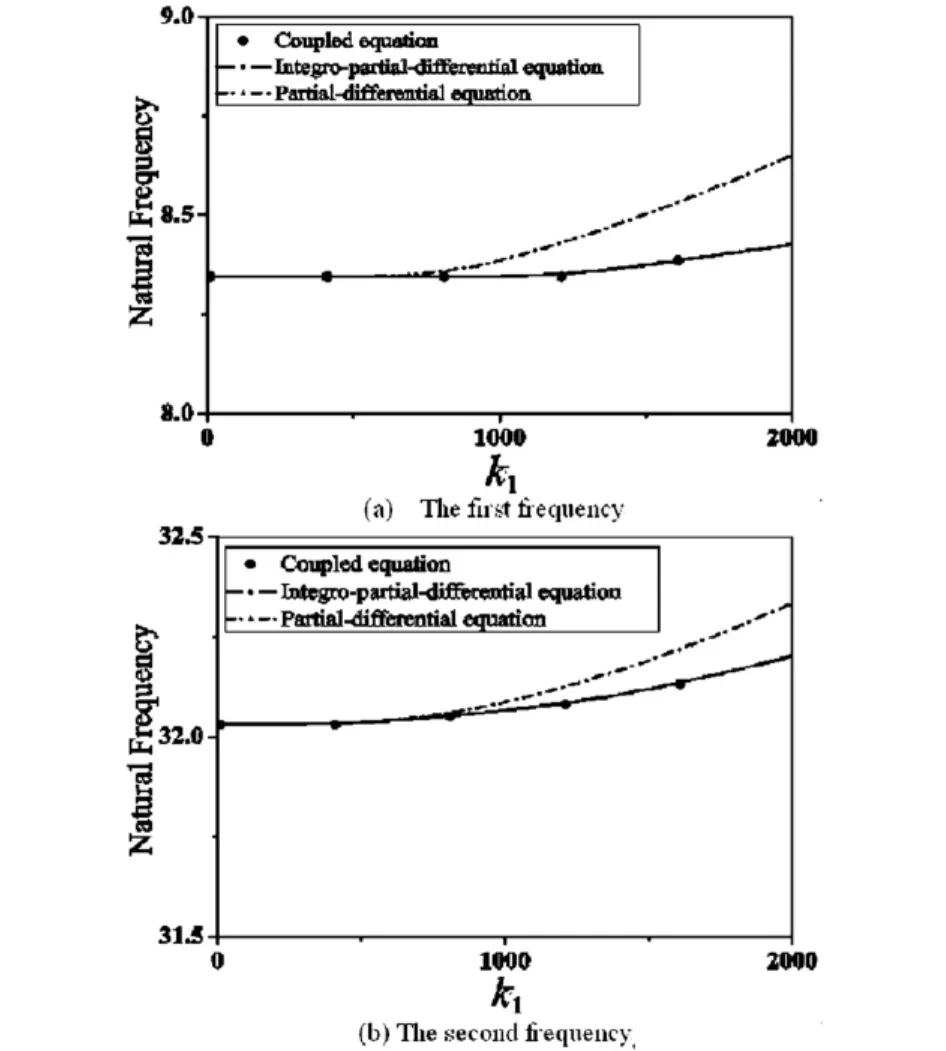
图9 非线性自由振动频率比较Fig．9 Comparison on the sub － critical natural frequencies

从图9给出了随非线性系数变化的两组横向非线性模型与耦合模型横向部分振动频率比较．从图中可以看出，随着非线性系数的增大，两组横向非线性模型对应的自由振动梁的前两阶固有频率和平面耦合振动横向运动部分的频率有着相同的变化趋势，在非线性系数不大时，两组横向模型的数值结果与耦合模型横向分量基本重合，但是随着非线性系数增大到一定数值，非线性偏微分模型与耦合模型以及偏微分—积分模型间的差别迅速呈现，并逐渐增大．

Chen等［54］通过有限差分方法比较了两组轴向运动弦线横向非线性振动模型与耦合模型的接近程度，得到的结论和梁模型对比中得到的结论完全相同．

以上的比较都是针对亚临界运动速度状态的．随着工业技术的发展，工程中对运动速度的要求越发增高．Ding等［55，56］通过微分求积方法和有限差分方法分别比较了经典边界以及混杂边界下两组横向非线性振动模型描述的超临界非平凡静平衡位形对平面运动中横向分量的接近程度．

对于简支边界、固定边界及混杂边界条件下，通过与径向和横向耦合模型的比较，实现从非平凡静平衡位形的角度比较两种横向非线性模型的有效性．研究发现，增大初始张力和梁的横截面积或者减小梁的轴向运动速度将使得系统非平凡静平衡位移变小，但是，对应于非线性偏微分－积分模型的数值结果都更加接近平面耦合模型，而对应于非线性偏微分模型的非平凡静平衡位移则较其他两组模型小．从图10(a)给出了简支边界下，微分求积法比较不同系统参数的钢材料的梁的两组横向非线性振动模型与平面耦合模型的横向非平凡静平衡位形．从图10(b)给出了混杂边界下，有限差分法对非平凡静平衡位形的模型比较．

另外，Ding和 Chen［57］还通过超临界振动频率对两组横向模型进行了对比．研究结果表明，就第一阶固有频率而言，对应于非线性偏微分模型的数值结果随着弯曲刚度的增大越加接近几乎重合的其他两组模型．从图11给出了不同运动速度下，两组横向非线性振动模型与平面耦合模型的超临界局部线性化后四阶Galerkin截断计算简支边界下固有频率的比较．通过观察发现，对应于非线性偏微分－积分模型的数值结果和平面耦合模型的数值结果基本重合，同时，对应于非线性偏微分模型的数值结果较大一些，而且这种差别随着轴向速度的增大而增大．

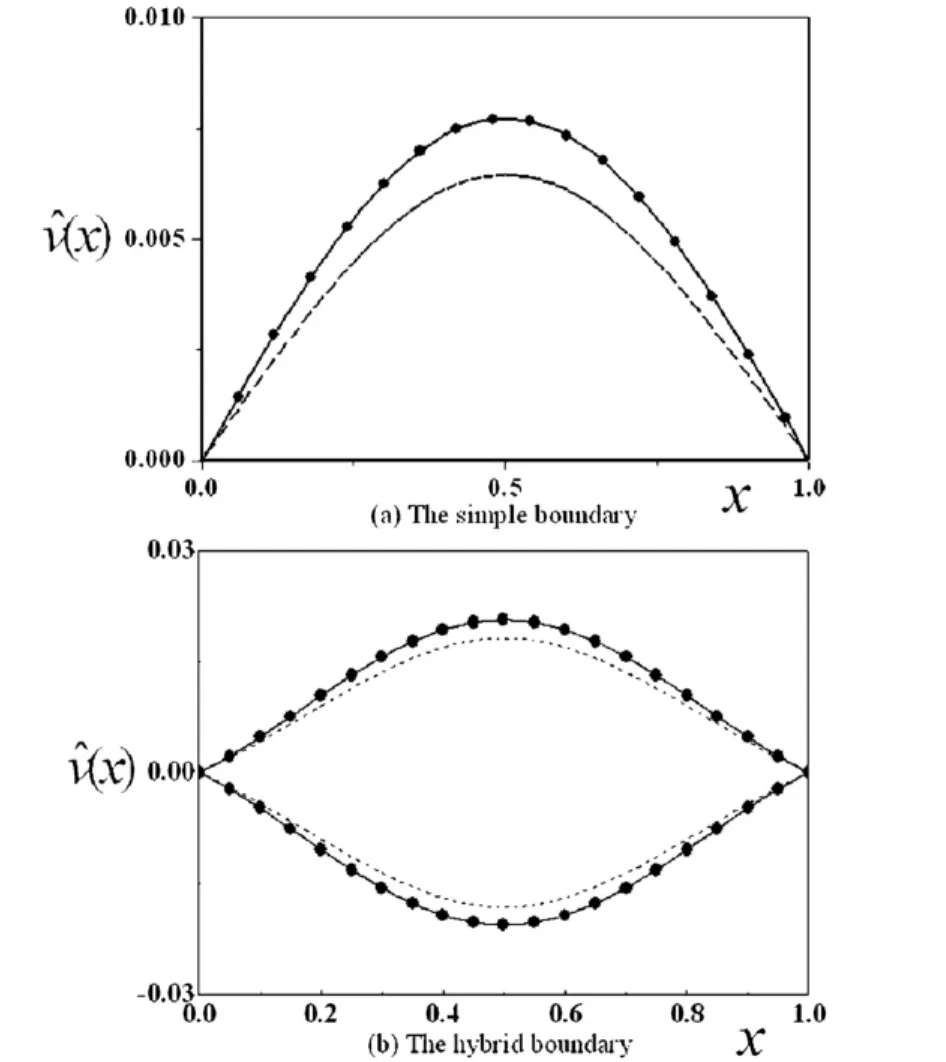
图10 超临界非平凡静平衡位形比较Fig．10 Comparison on the super－ critical non － trivial equilibria

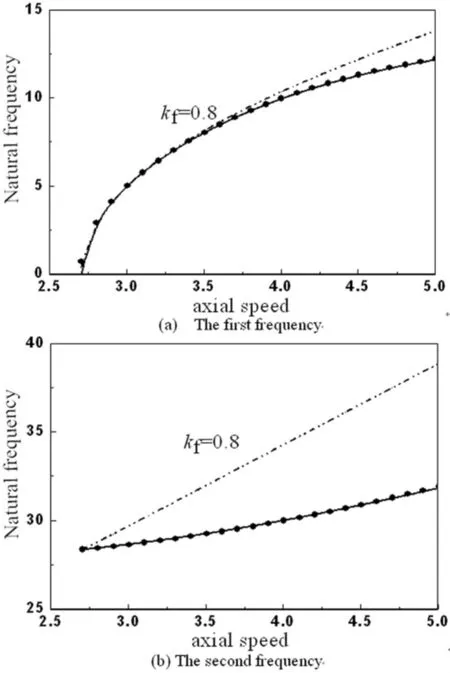
图11 简支边界下超临界振动频率比较Fig．11 Comparison on the super－ critical natural frequencies under simple boundaries

为了进一步研究初始振幅和非线性系数对超临界固有频率的影响，Ding等［58］也通过有限差分法结合离散Fourier变换比较了两组模型描述的轴向运动梁非线性振动频率与平面耦合振动横向部分的运动频率．数值研究表明，在超临界速度范围内，对于不同的弯曲刚度、轴向速度、非线性系数和初始振幅，非线性偏微分－积分模型的数值结果均比非线性偏微分模型的数值结果更加接近耦合模型的数值结果．其中，自由振动幅度对第一阶临界速度附近的固有频率影响极大，而远离临界速度时，前两阶固有频率随着初始振幅的增大有减小的趋势;而且非线性系数和初始振幅对前两阶固有频率的影响趋势几乎是一致的，因为超临界固有频率与非线性系数和初始振幅的乘积有直接关系．当初始振幅足够小时，实际非线性系数对固有频率几乎没有影响．

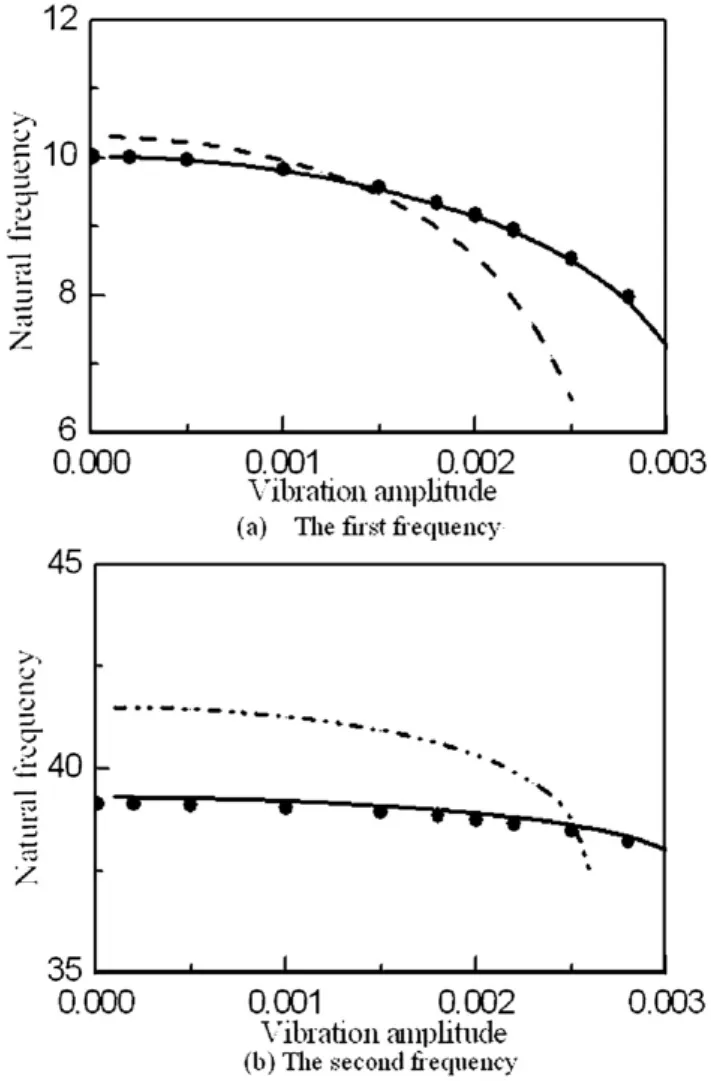
图12 固定边界下超临界振动频率比较Fig．12 Comparison on the super－ critical natural frequencies under clamped boundaries

从图12给出了固定边界下随初始振幅变化的两组横向非线性模型与耦合模型横向部分振动频率比较．从图中可以看出，随着非线性系数的增大，两组横向非线性模型对应的自由振动梁的前两阶固有频率和平面耦合振动横向运动部分的频率有着相同的变化趋势，而且非线性偏微分－积分模型和非线性耦合模型基本吻合，但是对应非线性偏微分方程的前两阶固有频率和耦合模型对应频率的差别却一直存在．这一点与亚临界速度范围内关于固有频率的结果稍有不同．

4 结束语

随着对轴向运动装置横向非线性振动研究的深入，两组横向振动模型也得到越来越广泛的应用．因而对这两组模型有效性、适用性的判定也显得越发迫切．本文综述了已有文献对这两组横向非线性振动模型比较的研究进展，发现现有的对比是在不同工况下、不同边界约束，以及不同速度范围内，比较两组模型描述的轴向运动梁横向响应与径向和横向平面耦合模型横向分量的差别．通过定性比较，分析结果表明，无论是自由振动、受迫振动还是参激振动工况，也无论两端简支、固定以及混杂边界，也无论是亚临界还是超临界运动轴向速度范围，两组横向模型的数值结果均与平面耦合模型横向部分的数值结果有着相同的趋势;通过定量比较发现，非线性偏微分－积分模型的数值结果总是更加接近平面耦合模型横向部分的数值结果．同样的结论也发生在不考虑抗弯刚度的两组轴向运动弦线横向振动模型．

虽然已经存在轴向运动弦线和梁的两组横向非线性振动模型的一些对比工作，但是对复杂梁模型，如轴向运动Rayleigh梁、Timoshenko梁横向非线性振动模型对比的研究工作还没有展开，而且工程中还存在一些其他的轴向运动连续体模型，例如网、板壳等，还不能确定两组横向非线性振动模型的数值对比中是不是存在其他结论．还有一个问题尤为迫切，就是仍然缺少决定性的证明工作，例如实验验证，即通过和实验数据对比，以确定两组模型的有效性和适用性．

因此，截止目前，相关于轴向运动连续体两组横向非线性振动模型对比的工作依然是一个开放性的课题，还有待进一步的研究．

1 陈立群．轴向运动弦线和梁的非线性动力学．见:张伟，胡海岩编．非线性动力学理论与应用的新进展．北京:科学出版社，2009:490～535(Chen L Q．Nonlinear dynamics of axially moving strings and beams．In:Zhang W，Hu H Y eds．Recent advances in theory of nonlinear dynamics with applications．Beijing:Science Press，2009:490～535(in Chinese))

2 Chen L Q．Nonlinear vibrations of axially moving beams．In:Evans TE，ed．Nonlinear Dynamics．Vukovar:Intech，2010:145～172

3 陈立群，丁虎．超临界轴向运动梁的分岔与振动．见:杨绍普，曹庆杰，张伟编．非线性动力学与控制的若干理论及应用．北京:科学出版社，2011:128～155(Chen L Q，Ding H．Bifurcation and vibration of axially moving beams in the supercritical regime．In Yang S P，Cao Q J，Zhang W eds．Theory of nonlinear dynamics and control with applications．Beijing:Science Press，2011:128 ～155(in Chinese))

4 Mote C D．On the nonlinear oscillation of an axially moving string．ASME Journal of Applied Mechanics，1966，33:463～464

5 陈立群，Zu J W．轴向运动弦线的纵向振动及其控制．力学进展，2001，31(4):535～546(Chen L Q，Zu J W．Transverse vibration of axially moving strings and control．Advances in Mechanics，2001，31(4):535 ～ 546(in Chinese))

6 Chen L Q．Analysis and control of transverse vibrations of axially moving strings．Applied Mechanics Reviews，2005，58(2):91～116

7 Chen L Q，Zhang W，Zu J W．Nonlinear dynamics in transverse motion of axially moving strings．Chaos，Solitons＆Fractals，2009，40(1):78 ～90

8 Öz H R，Pakdemirli M，Boyaci H．Non－linear vibrations and stability of an axially moving beam with time－dependent velocity．International Journal of Non-Linear Mechanics，2001，36(1):107 ～115

9 Özhan B B，Pakdemirli M．A general solution procedure for the forced vibrations of a continuous system with cubic nonlinearities:Primary resonance case．Journal of Sound and Vibration，2009，325(4－5):894 ～906

10 Özhan B B，Pakdemirli M．A general solution procedure for the forced vibrations of a system with cubic nonlinearities:Three－to－one internal resonances with external excitation．Journal of Sound and Vibration，2010，329(13):2603～2615

11 Marynowski K．Non－linear dynamic analysis of an axially moving viscoelastic beam．Journal of Theoretical and Applied Mechanics，2002，40(2):465～482

12 Marynowski K，Kapitaniak T．Zener internal damping in modelling of axially moving viscoelastic beam with time－dependent tension．International Journal of Non-Linear Me-chanics，2007，42(1):118～131

13 Sze K Y，Chen S H，Huang J L．The incremental harmonic balance method for nonlinear vibration of axially moving beams．Journal of Sound and Vibration，2005，281(3－5):611 ～ 626

14 Huang J L，Su R K L，Li W H，et al．Stability and bifurcation of an axially moving beam tuned to three－to－one internal resonances．Journal of Sound and Vibration，2011，330(3):471–485

15 陈树辉，黄建亮．轴向运动梁非线性振动内共振研究．力学学报，2005，37(1):57～63(Chen S L，Huang J L．Study on the international resonance of nonlinear vibration of axially moving beams．Acta Mechanica Sinica，2005，37(1):57～63(in Chinese))

16 Chen S H，Huang J L，Sze K Y．Multidimensional Lindstedt－Poincaré method for nonlinear vibration of axially moving beams．Journal of Sound and Vibration，2007，306(1－2):1～11

17 Chen L H，Zhang W，Liu Y Q．Modeling of nonlinear oscillations for viscoelastic moving belt using generalized Hamilton’s principle．ASME Journal of Vibration and A-coustics，2007，129(1):128 ～132

18 张伟，温洪波，姚明辉．黏弹性传动带1:3内共振时的周期和混沌运动．力学学报，2004，36(4):443～454(Zhang W，Wen H B，Yao M H．Periodic and chaotic oscillation of a parametrically excited viscoelastic moving belt with 1:3 internal resonance．Acta Mechanica Sinica，2004，36(4):443～454(in Chinese))

19 Zhang W，Yao M H．Multi－pulse orbits and chaotic dynamics in motion of parametrically excited viscoelastic moving belt．Chaos，Solitons and Fractals，2006，28(1):42～66

20 Chen L H，Zhang W，Yang F H．Nonlinear dynamics of higher－dimensional system for an axially accelerating viscoelastic beam with in－plane and out－of－plane vibrations．Journal of Sound and Vibration，2010，329(25):5321～5345

21 李映辉，高庆，蹇开林等．黏弹性带动力响应分析．应用数学和力学，2003，24(11):1191～1196(Li Y H，Gao Q，Jian K L，et al．Dynamic responses of viscoelatic axially moving Belt．Applied Mathematics and Mechanics，2003，24(11):1191～1196(in Chinese))

22 Ghayesh M H．Nonlinear transversal vibration and stability of an axially moving viscoelastic string supported by a partial viscoelastic guide．Journal of Sound and Vibration，2008，314(3－5):757 ～774

23 Ghayesh M H，Moradian N．Nonlinear dynamic response of axially moving，stretched viscoelastic strings．Archive of Applied Mechanics，2011，81(6):781–799

24 Ghayesh M H，Khadem S E．Rotary inertia and temperature effects on non－nonlinear vibration，steady－state response and stability of an axially moving beam with timedependent velocity．International Journal of Mechanical Sciences，2008，50(3):389～404

25 Ghayesh M H，Balar S．Non－linear parametric vibration and stability ofaxially moving visco－elastic Rayleigh beams．International Journal of Solids and Structures，2008，45(25－26):6451 ～6467

26 Chen L Q，Yang X D．Transverse nonlinear dynamics of axially accelerating viscoelastic beams based on 4－term Galerkin truncation．Chaos，Solitons and Fractals，2006，27(3):748～757

27 Tang Y Q，Chen L Q，Yang X D．Non－linear vibrations of axially moving Timoshenko beams under weak and strong external excitations．Journal of Sound and Vibration，2009，320(4－5):1078 ～1099

28 Thurman A L，Mote C D．Free，periodic，nonlinear oscillation of an axially moving strip．ASME Journal of Applied Mechanics，1969，36(1):83 ～91

29 Wickert J A．Non－linear vibration of a traveling tensioned beam．International Journal of Non-Linear Mechanics，1991，27(3):503～517

30 Ravindra B，Zhu W D．Low－dimensional chaotic response of axially accelerating continuum in the supercritical regime．Archive of Applied Mechanics，1998，68(3－4):195～205

31 Pellicano F，Zirilli F．Boundary layers and non－linear vibrations in an axially moving beam．International Journal of Non-Linear Mechanics，1998，33(4):691～711

32 Pellicano F，Vestroni F．Nonlinear dynamics and bifurcations of an axially moving beam．ASME Journal of Vibration and Acoustics，2000，122(1):21～30

33 Pellicano F，Vestroni F．Complex dynamic of high－speed axially moving systems．Journal of Sound and Vibration，2002，258(1):31～44

34 Chakraborty G，Mallik A K．Parametrically excited nonlinear traveling beams with and without external forcing．Nonlinear Dynamics，1998，17(4):301～324

35 Chakraborty G，Mallik A K，Hatwal H．Non－linear vibration of a travelling beam．International Journal of Non-Line-ar Mechanics，1999，34(4):655 ～670

36 Parker R G，Lin Y．Parametric instability of axially moving media subjected to multifrequency tension and speed fluctuations．ASME Journal of Applied Mechanics，2001(1)，68:49～57

37 Chen L Q，Zhao W J．The conserved quantity and the stability of axially moving nonlinear beams．Journal of Sound and Vibration，2005，286(3):663～668

38 丁虎，陈立群．轴向运动黏弹性梁横向非线性受迫振动．振动与冲击，2009，28(12):128～131(Ding H，Chen L Q．Transverse non－linear forced vibration of axially moving viscoelastic beam．Journal of Vibration and Shock，2009，28(12):128～131(in Chinese))

39 Zhang N H，Chen L Q．Nonlinear dynamics of axially moving viscoelastic strings based on translating eigenfunctions．Chaos，Solitons，and Fractals，2005，24(4):1065～1074

40 Chen L Q，Yang X D．Steady－state response of axially moving viscoelastic beams with pulsating speed:comparison of two nonlinear models．International Journal of Solids and Structures，2005，42(1):37～50

41 Chen L Q，Yang X D．Nonlinear free transverse vibration of an axially moving beam:comparison of two models．Journal of Sound and Vibration，2007，299(1－2):348 ～354

42 Yang X D，Chen L Q．Non－linear forced vibration of axially moving viscoelastic beams．Acta Mechanica Solida Sinica，2006，19(4):365～373

43 Ghayesh M H，Balar S．Non－linear parametric vibration and stability analysis for two dynamic models of axially moving Timoshenko beams．Applied Mathematical Modelling，2010，34(10):2850～2859

44 Ding H，Chen L Q．Approximate and numerical analysis of nonlinear forced vibration of axially moving viscoelastic beams．Acta Mechanica Sinica，2011，27(3):426–437

45 Chen L Q，Ding H．Steady－state responses of axially accelerating viscoelastic beams:Approximate analysis and numerical confirmation．Science in China Series G:Physics，Mechanics and Astronomy，2008，51(11):1707～1721

46 Chen L Q，Chen H，Ding H，et al．Non－linear combination parametric resonance of axially accelerating viscoelastic strings constituted by the standard linear solid model．Science in China E:Technological Sciences，2010，53(3):645～655

47 Chen L Q，Chen H．Asymptotic analysis on nonlinear vi－bration of axially accelerating viscoelastic strings with the standard linear solid model．Journal of Engineering Mathematics，2010，67(3):205～218

48 Chen L Q．Principal parametric resonance of axially accelerating viscoelastic strings constituted by the Boltzmann superposition principle．Proceedings of the Royal Society of London A，2005，461(2061):2701～2720

49 Ding H，Chen L Q．On two transverse nonlinear models of axially moving beams．Science in China Series E:Technological Sciences，2009，52(3):743～751

50 Chen L Q，Ding H．Two nonlinear models of a transversely vibrating string．Archive of Applied Mechanics，2008，78(5):321～328

51 Chen L Q，Ding H．Steady－state transverse response in coupled planar vibration of axially moving viscoelastic beams．Journal of Vibration and Acoustics，2010，132:011009－1－011009－9

52 Ding H，Chen L Q．Nonlinear models for transverse forced vibration of axially moving viscoelastic beams．Shock and Vibration，2011，18(1):281～287

53 Ding H，Chen L Q．Natural frequencies of nonlinear vibration of axially moving beams．Nonlinear Dynamics，2011，63(1－2):125 –134

54 Chen L Q，Ding H．Two nonlinear models of a transversely vibrating string．Archive of Applied Mechanics，2008，78(5):321～328

55 Ding H，Chen L Q．Equilibria of axially moving beams in the supercritical regime．Archive of Applied Mechanics，2011，81(1):51～64

56 Ding H，Zhang G C，Chen L Q．Supercritical equilibrium solutions of axially moving beams with hybrid boundary conditions．Mechanics Research Communications，2011，38(1):52～56

57 Ding H，Chen L Q．Galerkin methods for natural frequencies of high－speed axially moving beams．Journal of Sound and Vibration，2010，329(17):3484～3494

58 Ding H，Zhang G C，Chen L Q．Supercritical vibration of nonlinear coupled moving beams based on discrete Fourier transform．International Journal of Non-Linear Mechanics，2012，47(10):1095～1104

*The project supported by the National Science Foundation of China(10932006，10902064)，Innovation Program of Shanghai Municipal Education Commission(12YZ028)and Shanghai Rising－Star Program(11QA1402300)

† Corresponding author E－mail:dinghu3@shu．edu．cn

ADVANCES IN NONLINEAR MODELS FOR TRANSVERSE VIBRATION OF AXIALLY MOVING BEAMS*

Ding Hu1†Chen Liqun1，2Zhang Guoce1
(1．Shanghai Institute of Applied Mathematics and Mechanics，Shanghai University，Shanghai200072，China)(2．Department of Mechanics，Shanghai University，Shanghai200444，China)

This paper summarized the advances in two transverse models for nonlinear vibration of axially moving beams．Based on a nonlinear model for planar vibration of axially moving beams with coupled transverse and longitudinal motion，the derivation of two nonlinear models of transverse vibration was reviewed．The comparisons between approximate analytical results based on the two models for free，forced and parametric vibration of axially moving beams were surveyed．The deviations of the numerical solutions to the two transverse models from the solution to the coupled equation for different vibrations were also summarized．Some problems for further investigations were discussed．

axially moving beams， vibration， nonlinear models， approximate analysis， numerical simulation

20 April 2012，

27 June 2012．

10．6052/1672－6553－2013－004

2012－04－20 收到第 1 稿，2012－06－27 收到修改稿．

*国家自然科学基金项目(10932006，10902064)，上海市教育委员会科研创新项目(12YZ028)和上海市青年科技启明星计划(11QA1402300)

E－mail:dinghu3@shu．edu．cn