大阻尼杆振动的广义多辛算法*
2013-09-17胡伟鹏邓子辰
胡伟鹏 邓子辰
(1.西北工业大学工程力学系,西安 710072)(2.上海交通大学机械系统与振动国家重点实验室,上海 200240)(3.大连理工大学工业装备结构分析国家重点实验室,大连 116023)
大阻尼杆振动的广义多辛算法*
胡伟鹏1,2†邓子辰1,3
(1.西北工业大学工程力学系,西安 710072)(2.上海交通大学机械系统与振动国家重点实验室,上海 200240)(3.大连理工大学工业装备结构分析国家重点实验室,大连 116023)
本文基于Bridges教授建立的多辛算法理论及其Hamilton变分原理,采用广义多辛算法研究了大阻尼杆的阻尼振动特性.引入正交动量后,首先将描述大阻尼杆振动的控制方程降阶为一阶Hamilton近似对称形式,即广义多辛形式;随后采用中点离散方法构造形式广义多辛形式的中点Box广义多辛离散格式;最后通过计算机模拟研究大阻尼杆振动过程中的耗散效应.研究结果表明,本文构造的广义多辛算法不仅能够保持系统守恒型几何性质,同时能够再现系统的耗散效应.
广义多辛, 保结构, 耗散, 哈密顿
引言
针对传统数值算法构造过程中忽视算法在保持原系统固有几何性质方面的性能,冯康先生于1984年在双微国际会议上提出了基于辛几何原理的辛算法[1],用于解决有限维 Hamilton体系数值求解过程中的保结构问题,其基本出发点是使得数值离散尽可能与原连续系统保持在统一框架下,即尽可能多地保持系统的固有几何性质,自此,开辟了保结构算法研究领域.
在数年的研究过程中,辛算法在天体动力学和分子动力学等研究领域得到了广泛应用[2,3],同时也暴露出其不足之处:空间依赖的连续系统并不能采用辛算法进行数值求解.基于此,Bridges教授在辛算法的基础上,针对无穷维Hamilton系统提出了多辛算法[4],用以在数值求解过程中保持系统的局部几何性质.然而,实际的力学系统,耗散效应是不可忽略的,耗散效应的存在破坏了系统的多辛对称性,这是多辛算法的一大“瓶颈”.近年来,胡伟鹏和邓子辰教授针对耗散Hamilton系统,提出了广义多辛算法[5],将保结构算法理论体系拓宽至耗散系统.
本文在广义多辛理论框架下,采用广义多辛算法研究了大阻尼杆的振动特性.首先通过正则变换,构造大阻尼杆振动控制方程的广义多辛形式,并研究阻尼耗散在广义多辛形式中的数学表述;随后,采用中点离散方法离散广义多辛形式,构造其中点Box广义多辛离散格式;最后利用该格式模拟大阻尼杆的振动,研究振动过程中的阻尼耗散效应.本文的研究将完善保结构算法理论体系,同时为耗散动力学系统的数值求解提供新的途径.
1 大阻尼杆振动方程的广义多辛形式
由于材料本构关系中含有阻尼项,杆件的振动需要考虑大阻尼的情形.单位长度悬臂大阻尼杆的一维自由振动控制方程往往可以表述如下:

其中:c为不可忽略的阻尼系数,α为纵向应力波的传播速度.由于阻尼项的存在,杆振动振幅将会逐渐减小,常规的数值算法难以得到精确的衰减速度和振动时间,因此,本文将为大阻尼杆的振动提供新的数值计算途径.
引入正交变换:v=∂tu,ω =∂xu,上述控制方程就可以转化为以下Hamilton体系下的一阶形式:
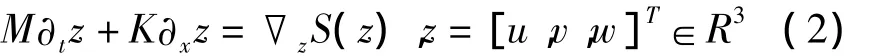
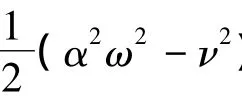

值得注意的是,一阶形式(2)是严格多辛形式的充分必要条件是:①一阶形式(2)是Hamilton系统,即存在Hamilton函数;②一阶形式(2)的系数矩阵必须都是严格反对称的.然而,本文涉及的大阻尼杆振动问题中,得到的系数矩阵中,由于阻尼的存在,矩阵K并不是反对称的,因此,依照广义多辛算法的概念,这里称一阶形式(2)为广义多辛形式.
实践证明,广义多辛形式虽然形式上不如多辛形式那么整齐,但是在保结构分析中具有重要的应用.将系数矩阵K作如下分解:

其中:K1=,K2=-,由这一规则得到唯一的分解结果:
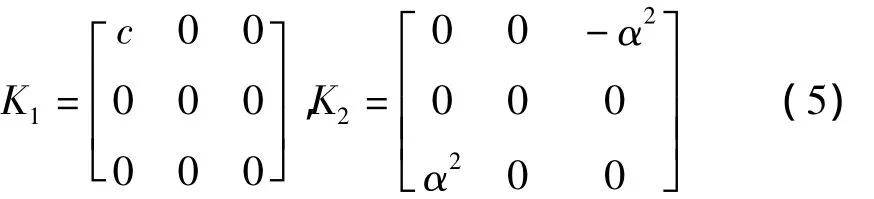
有了这一分解,就可以把阻尼耗散对系统性质的影响显式描述出来了.多辛算法最引人注目的地方是其满足三种基本的守恒律,即:多辛守恒律、局部能量守恒律和局部动量守恒律.由于非完全反对称性的系数矩阵的存在,广义多辛形式不可能完全满足以上三种守恒律,这里,由多辛理论不作证明地简要给出三种守恒律误差的表达式.
由多辛守恒律概念有,对于广义多辛形式(2),广义多辛守恒律误差可以表述为:

同时,由局部能量守恒律的概念,对于广义多辛形式(2),局部能量守恒律误差为:
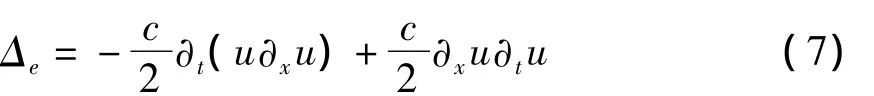
由于阻尼系数仅仅出现在状态变量z对空间偏微分部分,没有出现在状态变量z对时间偏微分部分,即只是在空间方向做功,而不存在对系统的冲量,因此,广义多辛形式(2)严格满足局部动量守恒律,这正是广义多辛形式的优势所在.
2 广义多辛离散及其数值实验
中心差分离散是最简单的差分离散方法,同时,也是构造多辛格式最简单,计算量最小的方法,因此,本文选用中心差分离散构造广义多辛形式(2)的保结构离散格式.
选取时间方向步长为Δt,空间方向步长为Δx,对计算区域进行均匀划分,状态变量z在(xi,tj)网格点上的近似值表示为,然后利用中点离散方法分别在空间方向和时间方向对广义多辛形式(2)进行差分离散,联立这两个方向的离散结果得到中点Box格式:
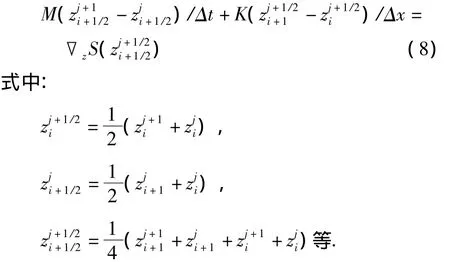
代入系数矩阵,状态变量及其Hamilton函数,并消去中间变量得到中点Box格式的等价形式:
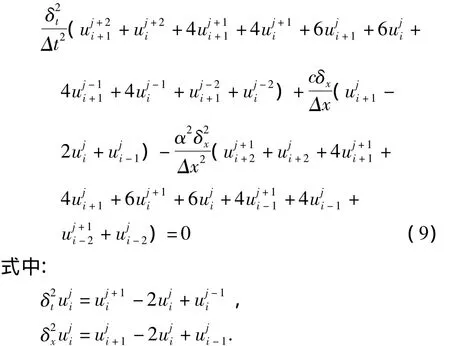
同时可以得到广义多辛守恒律误差和局部能量守恒律误差的差分离散形式.为了验证格式(9)的有效性,考虑以下边界条件:
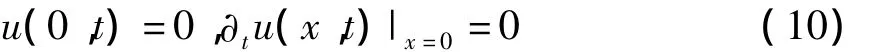

同时给定自由端单位横向位移作为初值条件:给定无量纲步长 Δt=0.1,Δx=0.05,并设定 α =1,采用格式(9)模拟杆件的阻尼振动,得到不同阻尼系数情况下杆自由端的振动曲线如图1.从图中可以看出,阻尼系数越大,杆件振动时间越短.为了进一步验证本文构造的算法在模拟阻尼耗散方面优于传统算法,在同样的步长及参数下,采用传统的欧拉离散方法离散方程(1),选取阻尼系数c=2,重新模拟悬臂杆的振动,得到的自由端振动曲线与采用本文广义多辛格式得到的振动曲线对比如图2,从对比中不难看出,本文构造的广义多辛算法得到的振动时间比常规算法得到的振动时间长,这说明广义多辛算法本身的阻尼小于常规算法本身的算法阻尼,也就是说,广义多辛算法能够更好地模拟系统的阻尼耗散效应,从而保持了系统的固有几何性质,这正是广义多辛算法的优势所在.
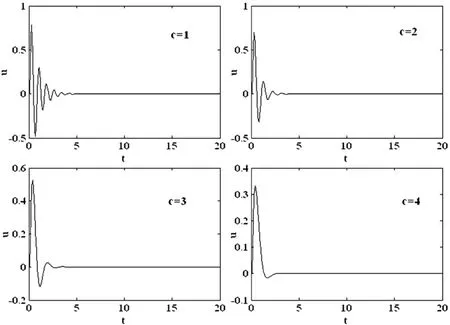
图1 不同阻尼系数下悬臂杆自由端振动曲线Fig.1 The vibration curves of the cantilever bar at the free end with different damping coefficients
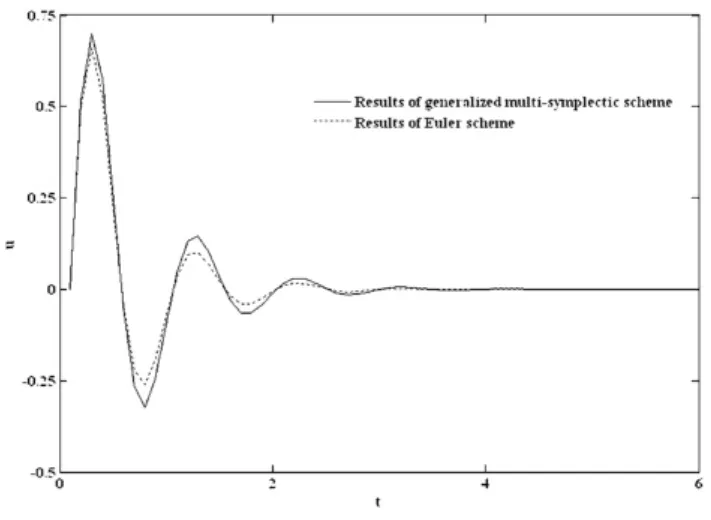
图2 算法耗散性质的比较Fig.2 The comparison of the dissipative propertiy
3 结论
本文通过采用广义多辛算法研究大阻尼悬臂杆的不同阻尼系数下阻尼振动特性,并讲数值结果与常规数值算法比较,得到如下结论:
(1)本文构造的广义多辛格式能够很好地模拟大阻尼杆的振动,阻尼系数越大,杆振动时间越短;
(2)与常规数值算法相比,本文构造的广义多辛算法能够更好的模拟系统的阻尼耗散效应,同时算法本身的耗散较小.
1 Feng K.On difference schemes and symplectic geometry,Proceeding of the 1984 Beijing Symposium on D.D.,Beijing:Science Press,1984,42~58
2 赵长印,廖新浩,刘林.辛算法在动力天文中的应用.计算物理,1992,(S2):812(Zhao C Y,Liao X H,Liu L.Application of symplectic algorithm in dynamic astronomy.Chinese Journal of Computational Physics,1992,(S2):812(in Chinese))
3 李延欣,丁培柱,吴承埙,金明星.A2B模型分子经典轨迹的辛算法计算.高等学校化学学报,1994,15(08):1181~1186(Li Y X,Ding P Z,Wu C Y,Jin M X.Symplectic algorithm calculation on the molecular classic track of the A2B model.Chemical Research In Chinese Universi-ties,1994,15(08):1181~1186(in Chinese))
4 Bridges T J.Multi-symplectic Structures and Wave Propagation.Mathematical Proceedings of the Cambridge Philosophical Society,1997,121(1):147~190
5 Hu W P,Han S M,Deng Z C,Fan W.Analyzing dynamic response of non-homogeneous string fixed at both ends.International Journal of Non-Linear Mechanics,2012,47(10):1111~1115
*The project supported by the National Natural Science Foundation of China(10972182,11002115,11172239),111 project(B07050)to the Northwestern Polytechnical University,the Science Foundation of Aviation of China(2010ZB53021),the China Postdoctoral Science Special Foundation(201003682),the NPU Foundation for Fundamental Research(JC20110259),the Doctoral Program Foundation of Education Ministry of China(20106102110019),the Open Foundation of State Key Laboratory of Mechanical System &Vibration(MSV-2011-21)and the Open Foundation of State Key Laboratory of Structural Analysis of Industrial Equipment(GZ0802)
† Corresponding author E-mail:wphu@nwpu.edu.cn
GENERALIZED MULTI-SYMPLECTIC METHOD FOR VIBRATION OF BIG DAMPING BAR*
Hu Weipeng1,2†Deng Zichen1,3
(1.Department of Engineering Mechanics,Northwestern Polytechnical University,Xi’an710072,China)(2.State Key Laboratory of Mechanical System&Vibration,Shanghai Jiao Tong University,Shanghai200240,China)(3.State Key Laboratory of Structural Analysis of Industrial Equipment,Dalian University of Technology,Dalian116023,China)
This paper studies the damping vibration properties of the big damping bar by the generalized multisymplectic method based on the Bridges’s multi-symplectic method and the Hamilton variation principle.Introducing orthogonal momenta,a first-order approximate symplectic form,named generalized multi-symplectic form is derived from the control equation of the big damping bar vibration firstly.And then a midpoint Box generalized multi-symplectic scheme is constructed by the midpoint method;Finally,the dissipation effect of the big damping bar vibration is studied.From the results of the numerical experiment,the good properties of the generalized multi-symplectic method are verified:satisfying the conservative properties of the system and reproducing the dissipation effect of the system.
generalized multi-symplectic, structure-preserving, dissipation, Hamilto generalized
20 April 2012,
9 June 2012.
10.6052/1672-6553-2013-001
2012-04-20 收到第 1 稿,2012-06-09 收到修改稿.
*国家自然科学基金(10972182,11002115,11172239)、111引智计划(B07050)、航空科学基金(2010ZB53021)、中国博士后科学基金特别资助(201003682)、西北工业大学基础研究基金(JC20110259),高校博士点基金(20106102110019),机械系统与振动国家重点实验室开放课题(MSV-2011-21)及大连理工大学工业装备结构分析国家重点实验室开放基金(GZ0802)资助项目
E-mail:wphu@nwpu.edu.cn
