变拓扑柔性多体系统接触碰撞动力学研究*

洪嘉振 刘铸永

(上海交通大学工程力学系，上海 200240)

变拓扑柔性多体系统接触碰撞动力学研究*

洪嘉振 刘铸永†

(上海交通大学工程力学系，上海 200240)

在实际工程领域中存在着大量接触碰撞等非连续动力学问题，现有的解决柔性多体系统连续动力学过程的建模理论与方法，已经无法解决或无法很好解决这些问题．本文基于变拓扑思想，提出了附加接触约束的柔性多体系统碰撞动力学建模理论;通过设计柔性圆柱杆接触碰撞实验，验证了所提出附加约束接触碰撞模型的有效性;针对柔性多体系统全局动力学仿真面临时间和空间的多尺度问题，提出多变量的离散方法，从而提高了柔性多体系统非连续动力学的仿真效率．

柔性多体系统， 接触碰撞， 变拓扑， 数值仿真， 实验研究

引言

近三十年来国内外学者在多体系统连续过程建模理论、计算方法和实验研究等方面做了大量的工作，取得了一系列重要科研成果，相继解决了动力刚化、微分代数方程数值求解、最优控制等重要问题，建立了程式化的多体系统刚柔耦合动力学建模理论和有效的数值求解算法，并形成了诸如ADAMS、DADS和RECDYN这样的大型工程软件，这些软件已经在众多工程问题的实践中经受了考验，大大提高了新产品的设计开发的效率．

然而在现代航空航天、机械制造等领域，高速、轻质的系统面临的动力学环境与过程越来越复杂．柔性多体系统动力学中，现有的解决连续动力学过程的建模理论与方法，已经无法解决或无法很好解决这些问题［1－6］．

例如，目前我国载人航天与未来空间站的航天器交会对接;现代航天器已经成为大型空间的机械系统，各类卫星太阳电池阵的展开，到位锁定时的接触碰撞;空间大型柔性部件(机械臂、太阳电池阵、大型天线阵等)的非连续驱动;铰链间隙引起的撞击等等．在这些非连续动力学过程中，系统的拓扑会发生突变，以其作用时间短、撞击力大给系统造成剧烈扰动，引起系统动力学性态的突变，对航天器机构动力学性态的灾难性影响已经引起了关注．

柔性多体系统非连续动力学过程的实质是若干不同拓扑系统连续过程的不断切换．也就是具有某个自由度的某种连接关系的一种机构的运动，突然改变为具有不同自由度的另一种机构的运动．当前最典型的非连续问题是接触碰撞．多体系统接触碰撞问题在力学本质上是一种非光滑、变边界的高瞬态、高非线性动力学过程．对这类问题的研究既要考虑柔性体变形运动与大范围运动之间的耦合，又要考虑碰撞动力学过程的合理建模，其中对碰撞过程的正确处理是解决多体系统碰撞动力学问题的关键．

现有的接触碰撞模型都还有不足之处．基于刚体假设的冲量动量方法虽然具有计算效率高、直观等优点，且对碰撞过程中出现的能量不协调等问题进行了很好的解决，仍然难以适应以上工程领域对碰撞力及系统碰撞动力学响应求解提出的需求．基于弹簧阻尼的连续碰撞力公式的出现在一定程度上克服了碰撞力难以求解的困难，并在工程领域中得到了相当广泛的应用，长期以来也为两个问题所困扰:碰撞力模型合理形式的选择和碰撞力方程中参数的合理辨识．这两个问题直接决定了仿真结果的可信性．目前存在的实验研究成果和方案往往只针对具体的个案，缺乏普适性．非线性有限元法、无网格等方法的优点是可以对碰撞动力学过程进行建模，但柔性体的大范围空间运动及弹性变形不加区分地采用惯性坐标系下的节点坐标表示，由此得到的动力学方程的广义坐标数目非常庞大，计算效率低，难以应用到复杂的柔性系统动力学分析中．同时由于该方法无法区分刚体运动和弹性变形，给控制系统的设计带来难以逾越的困难．因此，迫切需要提出一种柔性多体系统碰撞动力学过程全局仿真方法，以满足柔性多体系统碰撞动力学对通用性、高效率、准确性和可靠性的要求．

本文基于非连续动力学过程通过合理切换可分解为若干连续过程的思路，将复杂机械系统变拓扑过程统一在通用的柔性多体系统模型下，研究通用与高效的柔性多体系统刚柔耦合动力学模型与接触碰撞动力学模型，解决变拓扑柔性动力学全局仿真系统切换的关键问题．采用附加约束的方法能够真正从物理上对接触碰撞问题进行准确描述，从而实现柔性多体动力学全局仿真．通过数值仿真和实验研究验证本文所提出的附加约束方法的有效性．针对变拓扑柔性多体系统动力学的非连续、非光滑特性和存在时间及空间的多尺度问题，提出多变量方法，研究了柔性多体系统非连续动力学全局仿真计算方法．

1 接触碰撞动力学模型

1．1 附加约束方法

基于弹簧阻尼的多体系统连续碰撞力模型目前在工程领域得到广泛应用．然而该方法将碰撞力作为物体间嵌入量和嵌入速度的函数来计算，且需要人工设置函数中的参数．仿真结果过分依赖于人工参数的选择，况且嵌入量本身也不符合物理实际［1－2］．

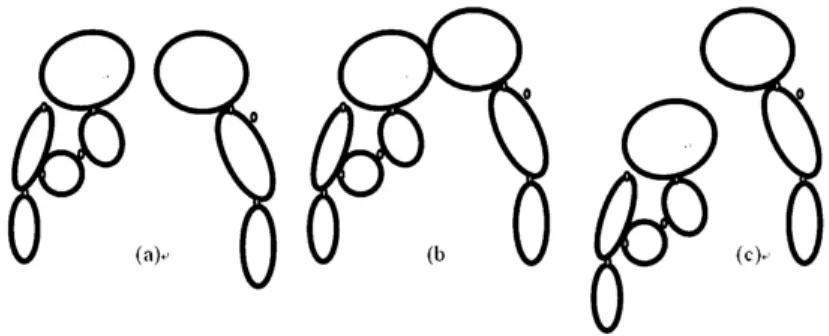
图1 不同碰撞阶段碰撞Fig．1 Different Stages of impact

如图1所示，本文将柔性多体碰撞分为碰撞前、碰撞阶段、碰撞后三个过程，采用附加接触约束描述碰撞阶段的动力学过程，将上述三个过程的动力学方程形式统一．通过引入碰撞检测机制，实现拓扑模型的自动切换．将此方法称为附加接触约束方法．

柔性多体系统碰撞前和碰撞后动力学方程为［3］:

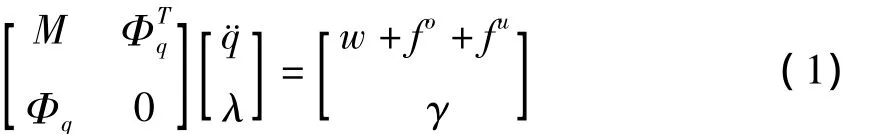
这里M是柔性多体系统质量矩阵，Φq是多体系统铰约束的雅克比矩阵，λ是与铰约束对应的拉格朗日乘子矢量，w，fo和fu分别是柔性体系统受到的惯性力矢量，广义外力矢量和广义变形力矢量，γ是加速度约束方程的右端项．

碰撞阶段，接触位置位移相同，故附加接触位移约束方程为:

将其写成加速度约束方程的形式，即

结合式(1)，柔性多体系统碰撞阶段动力学方程为:

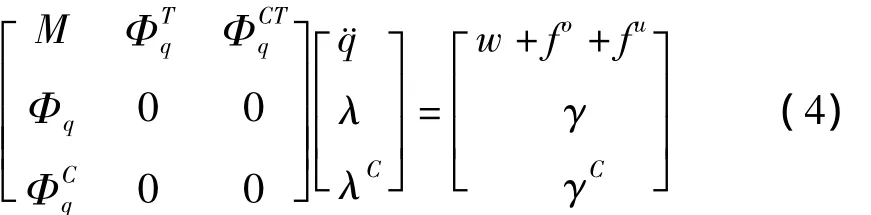
和γC是碰撞过程中附加接触约束方程的左端项和右端项矩阵．

1．2 与LS－DYNA罚函数法计算结果比较

如图2所示，水平面上柔性杆B1与柔性杆B2的中心处发生碰撞，B1和B2的轴线相互垂直．B1为自由杆，B2两端受固定端约束．碰撞发生时B1的速度为0．2m/s，B2处于静止状态．杆的几何和材料参数见表1，B1和B2扁平等厚，故该问题可简化为平面问题处理．对此算例分别用ACCM法和LS－DYNA罚函数法进行仿真．使用计算机的配置参数为 AMD Athlon(tm)64 processor 3200+，2．01GHz，1GB 的内存．

表1 杆的几何和材料参数Table 1 Geometrical and material data

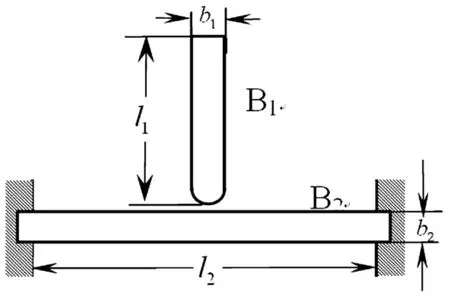
图2 柔性杆碰撞示意图Fig．2 Collision between flexible bars

在利用LS－DYNA罚函数方法仿真时，需要人工设定罚因子．对同一个罚因子，计算步长不同，计算结果也不同．随着计算步长的减小，计算结果将趋于一个稳定解．对于本算例，表2列出了利用LS－DYNA罚函数方法仿真时，对于不同的罚因子获得稳定解所需要的最大时间步长，以及相应的CPU仿真时间．利用本文提出的方法，克服了这种对罚因子的依赖．

表2 各方法获稳定解所需时间步长与CPU计算时间Table 2 Time step required for stable solution and CPU computing time

此外，从图3－6的罚函数方法计算结果(虚线)发现，利用罚函数方法，对于不同的罚因子(依次分别对应罚因子为 0．01、0．1、1．0 和 5．0 时的情况)，所得到的稳定解是不同的．过小的罚因子(图3)会造成仿真结果严重失真．当罚因子增大到一定程度，仿真结果将变化不大(图5－图6)，可以认为仿真结果收敛于“精确解”．比较计算结果，本算例能得到“精确解”的罚因子应大于1．0．理论上罚因子，得到的解为精确解．但实际计算中，罚因子取值越大，为了得到稳定结果，则计算步长要取得非常小，严重影响了计算效率．可见，为了兼顾计算精度和计算效率，罚因子取值不能无限制大，必须要经过多次试算来选择合适的罚因子．

从图3－图6的ACM方法计算结果(实线)发现，这种计算“精确解”依赖于罚因子的不足，对于本文提出的方法不存在．

图3 ACCM与DYNA罚因子为0．01的碰撞力曲线Fig．3 Contact force(ACCM and LS － DYNA fs=0．01)

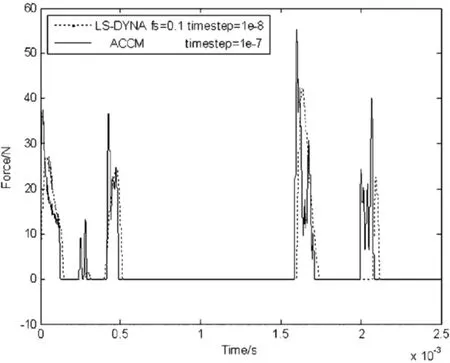
图4 ACCM与DYNA罚因子为0．1的碰撞力曲线Fig．4 Contact force(ACCM and LS － DYNA fs=0．1)

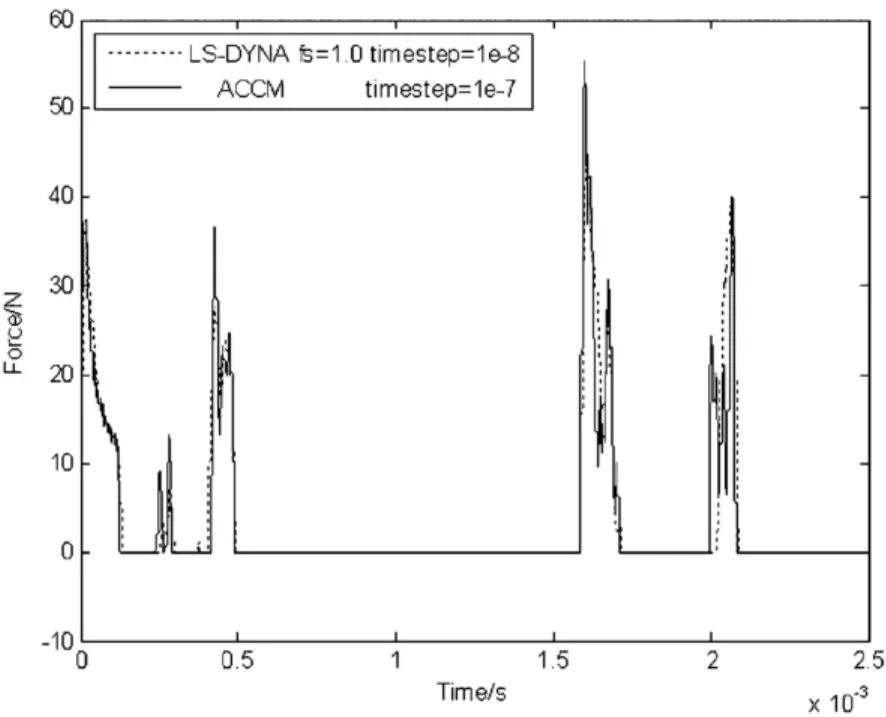
图5 ACCM与DYNA罚因子为1．0的碰撞力曲线Fig．5 Contact force(ACCM and LS － DYNA fs=1．0)

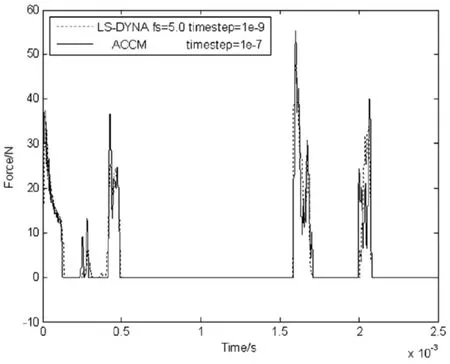
图6 ACCM与DYNA罚因子为5．0的碰撞力曲线Fig．6 Contact force(ACCM and LS － DYNA fs=5．0)

2 接触碰撞试验研究

2．1 接触碰撞试验装置

为了验证本文提出的碰撞动力学过程建模方法的正确性，设计了两圆柱铝杆碰撞实验．如图7所示为实验装置示意图．该实验装置包含以下部件:两圆柱截面铝杆，Polytech Gmbh公司制造的OFV－300F型激光测振仪(LDV)、动态应变仪、1．5V直流电源和金属实验台架．碰撞过程中杆2的速度由激光测振仪进行测量，它由激光扫描头、控制器、连接箱和工作站组成．

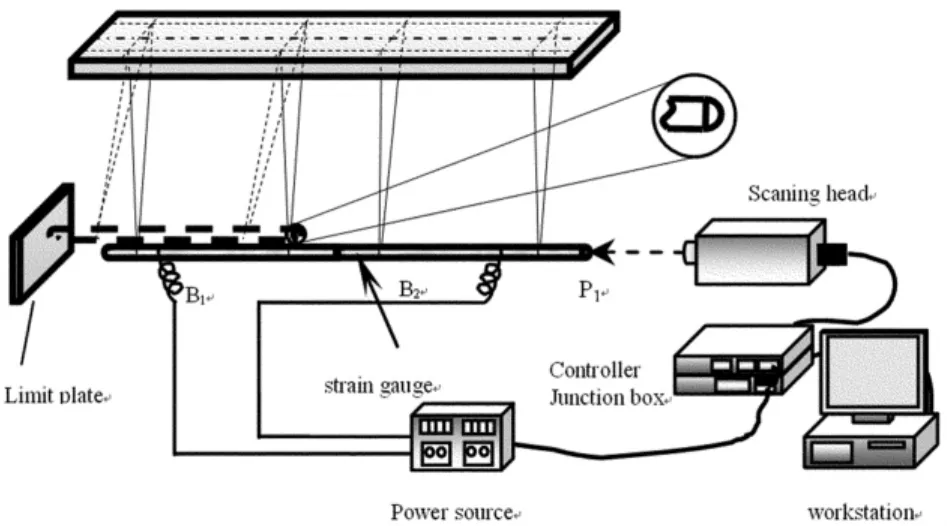
图7 实验装置示意图Fig．7 Experiment equipments

如图7所示，一开始将杆B1从限制板上某一确定位置处释放．然后杆B1自由下摆，当下摆到水平位置处时，B1杆达到最大速度，即碰撞前初始速度，碰撞前B1的速度通过激光测振仪进行测量．经过25次测量，得到碰撞时刻杆 B1的速度为0．21m/s，其中速度平均误差小于0．5%．在碰撞实验中碰撞力的时间历程是一个关注点．在一些实验中，直接通过压电传感器测量碰撞力变化历程然而在实验过程中压电传感器必须固定在物体碰撞表面上，这样原有的碰撞界面就会受到损坏，导致压电传感器测量得到的碰撞力并非原来的碰撞力．因此，只能通过速度或者应变间接地验证出仿真结果中碰撞力的正确性．

在本部分，将采用不用的建模方法对两杆碰撞动力学过程进行数值仿真，其中碰撞过程中杆的几何和运动学参数如表3所示．

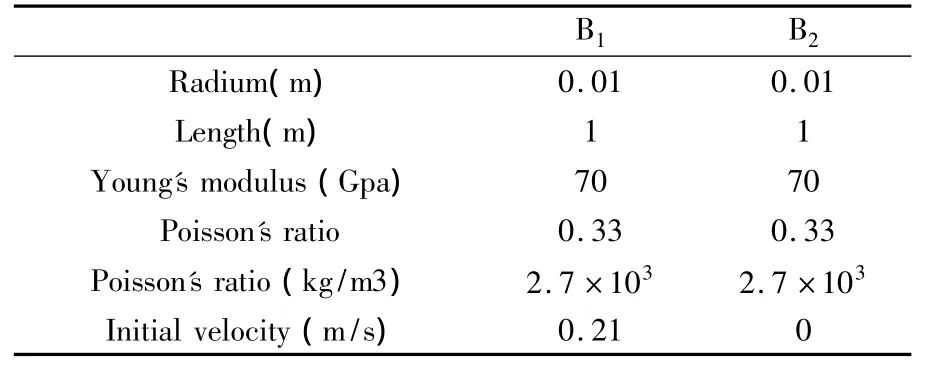
表3 柔性杆的材料和运动学参数Table 3 Geometrical and material data

2．2 试验结果与仿真结果比较

如图8－11所示，可以看出，本文提出的附加约束方法仿真结果与实验结果较为吻合．而弹簧阻尼模型仿真结果与实验结果之间存在着很大的误差．如图10所示，为ACM方法仿真结果与实验结果在杆B2上不同点处速度曲线比较，其中杆B2上11个测量点沿杆轴向方向均匀分布．由于图中存在22条曲线，限于空间，没有给出每条曲线的图标．从曲线的比较可以看出，几乎所有仿真结果与实验结果都吻合地很好，这意味着由ACM方法仿真得到的碰撞过程与真实的碰撞过程相吻合．

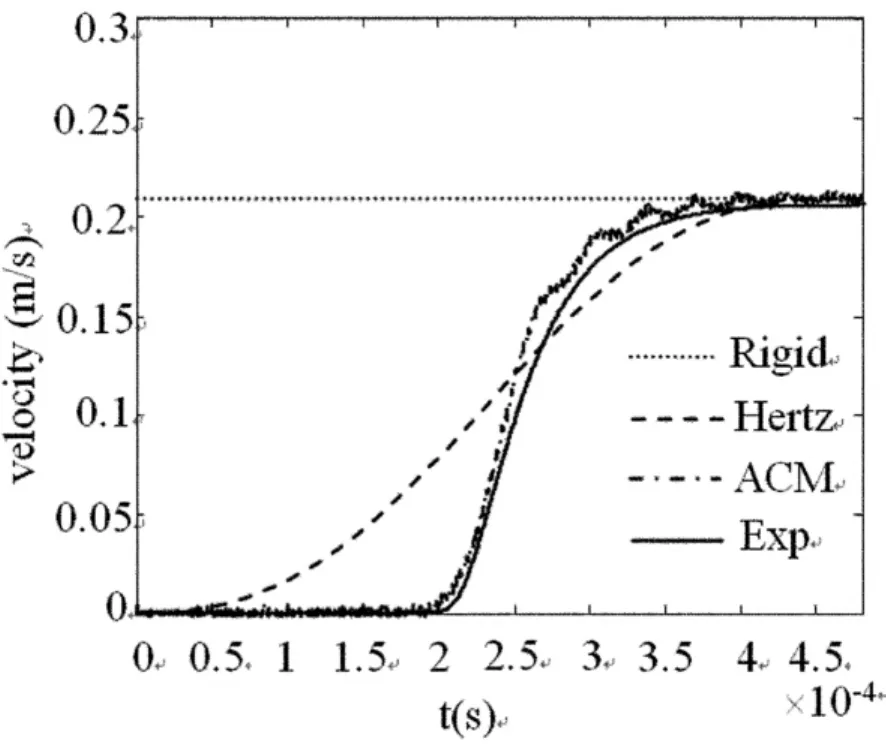
图8 B2端部速度响应曲线Fig．8 Velocity response of B2top

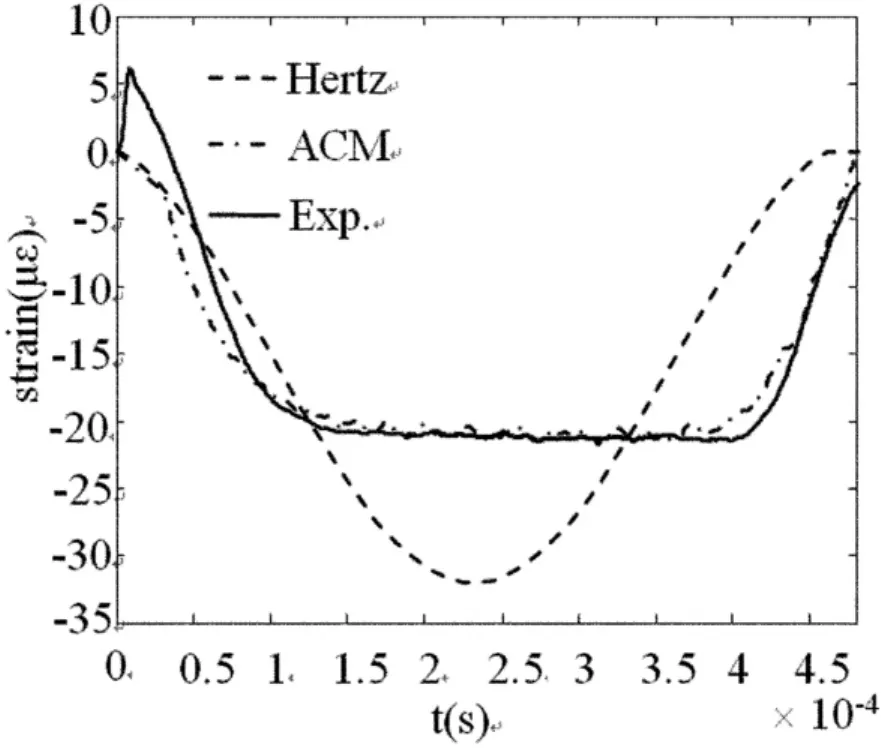
图9 B2上距接触端上2cm处P点应变Fig．9 Strain of Point P in B2(2cm from top)

图10 杆B2上11个点的速度Fig．10 Velocity response of 11 points in B2

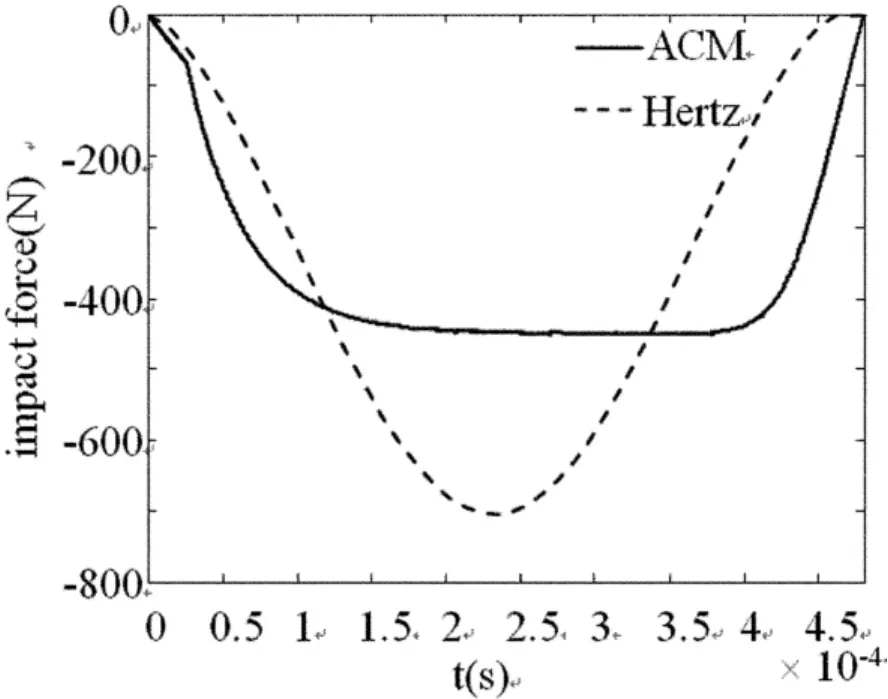
图11 碰撞力曲线Fig．11 Contact force

从图11的仿真结果上看，可以看出在碰撞过程中不同位置处的速度并不同时改变，这说明刚体碰撞假定中各点速度同时突然变化的假定与实际情况之间存在着一定得差异．根据如图7所示实验结果，同一速度条件下100cm处和0cm处的时间差为1．9561e－004s，通过实验数据可以得到弹性波在铝杆表面的传播速度为5．1122e+003m/s，而一维情况下弹性波的理论传播速度是5．0918e+003，相对误差是0．4006%．这说明碰撞引起的速度扰动在弹性介质中的确以弹性波的形式进行传播，同时验证了碰撞动力学方程的速度跳跃条件的解释符合真实情况．如图8所示为弹簧阻尼模型和ACM方法仿真得到碰撞力时间历程比较．由于碰撞力难以通过实验的方法直接精确测量，因此只能通过仿真计算得到碰撞力的时间历程．从图8－11中ACM仿真结果和实验结果的对比上看，可以得出由ACM方法仿真得到碰撞过程与实际的物理碰撞过程一致，这样就可以得出由ACM方法仿真得到的碰撞力与真实碰撞力一致．此外，从图中可以看出这样一个复杂的碰撞力变化历程很难通过简单的弹簧阻尼模型进行建模．

3 多变量仿真算法

3．1 多变量离散方法

为提高全局仿真的计算效率，提出了多变量离散方法．如图12所示，两多体系统1和2发生接触/碰撞．其中，系统1包含m个物体，系统2包含n个物体，发生碰撞的物体为系统1中的第i个物体Bi与系统2中的第j个物体Bj．对发生碰撞的物体Bi、Bj进行分区，接触局部区域采用非线性有限元方法，其他区域用浮动参考系方法．对于接触区域，以系统1上的接触域为从物体，系统2上的接触域为主物体．

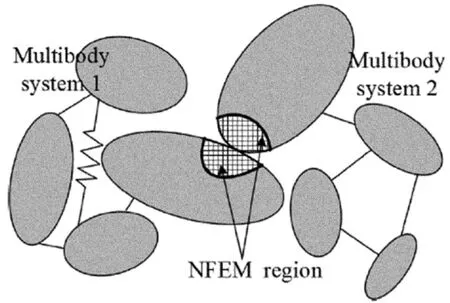
图12 多变量离散方法Fig．12 Multi－ variable discrete method

3．2 多变量方法的仿真结果

图13所示铅垂面内双摆由B1、B2两个物体组成．B1为刚体，长为0．5m，质量为5kg，对质心的转动惯量为0．15kgm2．B2为平面弹性体，表4给出了B2的材料参数，同时给出了双摆的初始位置和速度．双摆自水平位置已一定初速度下落，撞击刚性地面后又反弹．其中，表面与地面静摩擦系数为0．7，动摩擦系数为0．6．B2物体可能发生碰撞局部的区域采用有限元节点坐标，其它区域采用浮动基位形坐标和模态坐标，两部分交界如图13所示，浮动基原点取在O2点，横轴附着于B2两节点上．

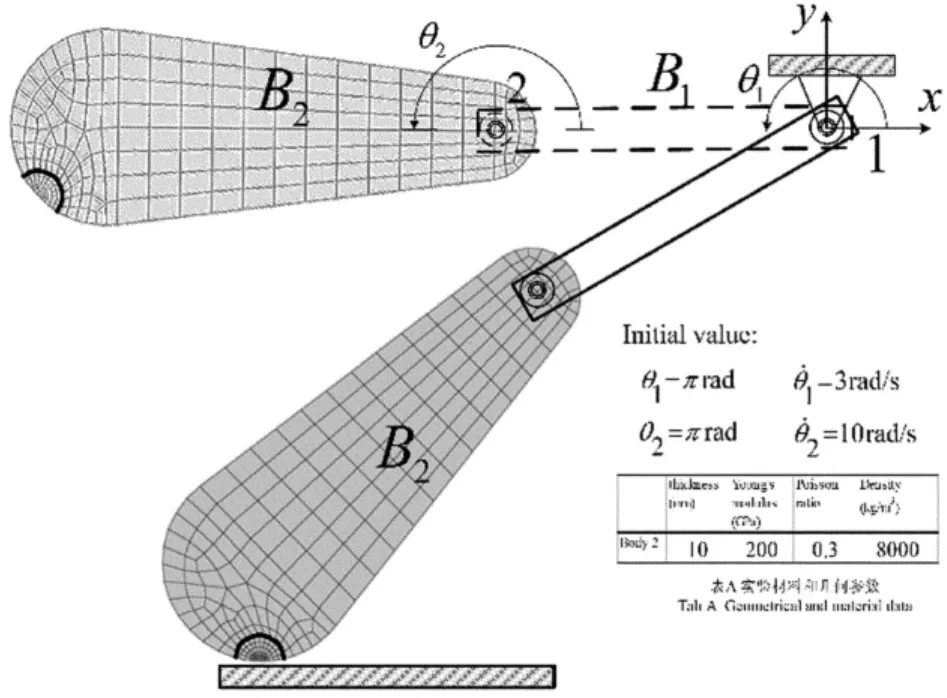
图13 双摆与地面碰撞Fig．13 Impact between double － pendulum with ground

表4 双摆的材料和运动学参数Table 4 Geometrical and material data of double pendulum

本算例中，对于碰撞过程采用显式法求解，对于未接触和接触分离后的阶段采用隐式法求解．隐式法时间步长取h=5E－3s，未接触阶段和接触分离后阶段分别只用到了19和30个时间步．显式法时间步长取0．2E－6s，碰撞阶段用到了3000个时间步．本例约有120个自由度(B1有3个自由度，B2浮动基3个自由度+20阶模态+47有限元节点)，三个阶段的仿真计算均在半分钟至一分钟内完成(CPU:AMD Athlon(tm)64 Processor 3200+，2．01GHz)．说明多变量方法具有较高的计算效率．

图14 碰撞力曲线Fig．14 Contact force

4 结论

本文基于非连续动力学过程通过合理切换可分解为若干连续过程的思路，将复杂机械系统变拓扑过程统一在通用的柔性多体系统模型下，研究通用与高效的柔性多体系统刚柔耦合动力学模型与接触碰撞动力学模型，解决变拓扑柔性动力学全局仿真系统切换的关键问题．基于变拓扑思想，本文提出了附加接触约束的柔性多体系统碰撞动力学建模理论;通过设计柔性圆柱杆接触碰撞实验，验证了所提出附加约束接触碰撞模型的有效性;针对柔性多体系统全局动力学仿真面临时间和空间的多尺度问题，提出多变量的离散方法，从而提高了柔性多体系统非连续动力学的仿真效率．

1 Diolaiti N，Melchiorri C，Stramigioli S．Contact impedance estimation for robotic systems．IEEE Transactions on Robotics，2005，21(5):925～935

2 Zhang Y，Sharf I．Experimental validation of nonlinear compliant contact force models．Proceedings of the ASME 2007 International Design Engineering Technical Conferences ＆ Computers and Information in Engineering Conference，September 4–7，2007，Las Vegas，Nevada，USA

3 洪嘉振．计算多体系统动力学．北京:高等教育出版社，1999(Hong Jiazhen．Computational dynamics of multibody systems．Beijing:Higher Education Press，1999(in Chinese))

4 王礼立．应力波基础．北京:国防工业出版社，2005(Wang L L．Foundation of stress waves．Beijing:National Defence Industry Press，2005(in Chinese))

5 Thomas Klisch．Contact mechanics in multibody system．Multibody System Dynamics，1998，2(4):335～354

6 黄筑平．连续介质力学基础．北京:高等教育出版社，2003(Huang Z P．Fundamentals of continuum mechanics．Beijing:Higher Education Press，2003(in Chinese))

7 董富祥．刚柔耦合多体系统碰撞动力学建模理论与实验研究［博士学位论文］．上海:上海交通大学，2010(Dong Fuxiang．Study of modeling theory and experiment for impact dynamics of rigid－flexible coupling multibody systems．［PhD Thesis］．Shanghai:Shanghai Jiao Tong U－niversity，2010(in Chinese))

*The project supported by the National Natural Science Foundation of China(11132007，11202126)，Foundation of Doctoral Program of Ministry of Education of China(20090073110009)and Natural Science Foundation of Shanghai(11ZR1417000)

† Corresponding author E－mail:zhuyongliu@sjtu．edu．cn

STUDY ON CONTACT/IMPACT DYNAMICS OF FLEXIBLE MULTIBODY SYSTEM WITH TOPOLOGY VARIABLE*

Hong Jiazhen Liu Zhuyong†
(Department of Engineering Mechanics，Shanghai Jiao Tong University，Shanghai200240，China)

There is an increasing number of discontinuous dynamics problems，such as contact and impact，in the engineering field．The known modelling theories and methods，which are used to solve the continuous dynamics of flexible multibody systems，are not able to solve those problems or to solve those problems perfectly．In this paper，an appending constraint method was proposed to solve the contact/impact dynamics of flexible multibody system based on the idea of topology variable．The impact experiment of flexible bars was designed to verify the validity of the proposed method．At last，a multi－variable method was proposed to solve the multi－scale problems of time and space when the global simulation of the discontinuous dynamics of flexible multibody systems was carried out，and the computational efficiency of the global simulation of the discontinuous dynamics of flexible multibody systems was improved by using this method．

flexible multibody sytem， contact/impact， topology variable， numerical simulation， experimental research

11 April 2012，

15 June 2012．

10．6052/1672－6553－2013－002

2012－04－11 收到第 1 稿，2012－06－15 收到修改稿．

*国家自然科学基金重点项目(11132007，11202126)，博士点基金(20090073110009)、上海市自然科学基金(11ZR1417000)资助

E－mail:zhuyongliu@sjtu．edu．cn