外接球问题“心”在哪里

浙江省临海市回浦中学 李昌湛 （邮编：317000）

在组合体中，有一类是几何体的外接球问题，解决这类问题的关键是确定外接球球心的位置.本文介绍几种找几何体外接球球心的方法，仅供参考.

1 利用直角三角形斜边的中点找球心

例1 （2009湖南卷）在半径为13的球面上有A，B，C三点，AB＝6，BC＝8，CA＝10，则球心到平面ABC的距离为＿＿＿＿.

解 ∵AB＝6，BC＝8，CA＝10，

∴∠ABC＝，

故球心到平面ABC的距离为12.

例2 如图2，在四边形ABCD中，AB＝BC＝CD＝1，AB⊥BD，BC⊥CD，将 △ABD沿BD折起，使得平面ABD⊥平面BCD，则该几何体的外接球的表面积等于（ ）

解 如图2，在四面体A－BCD中，

∵平面ABD⊥平面BCD，AB⊥BD，

∴AB⊥平面BCD，又CD⊥BC，

由三垂线定理知CD⊥AC，即AD是Rt△ABD和Rt△ACD的公共斜边，取斜边AD的中点O，连结OB，OC，则OA＝OB＝OC＝OD，∴四面体A－BCD的外接球球心即为O，∴外接球的半径R＝OA＝AD＝，∴S球＝4πR2＝＝3π，故选A.

例3 一个几何体的三视图如图3所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为（ ）

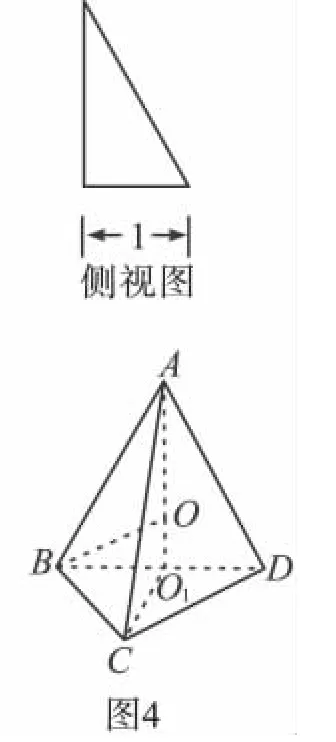
解 由三视图作出原几何体是三棱锥ABCD，如图4所示.

平面ABD⊥平面BCD，取BD的 中 点O1，连结AO1，CO1，

因△ABD是边长为2的正三角形，△BCD是等腰直角三角形，且BC＝CD＝，∠BCD＝90°，有AO1⊥平面BCD，则球心O在线段AO1上，连结BO，设外接球的半径为R，在Rt△BOO1中，因BO2＝BO12＋，即R2＝12＋－R）2，解得R＝，∴S球＝4πR2＝，故选B.

评注 因为直角三角形斜边的中线长等于斜边的一半，所以斜边的中点到该直角三角形三个顶点的距离相等，利用这一性质可找出过直角三角形三个顶点的几何体的外接球球心.

2 利用斜三角形的外心找球心

例4 （2010宁夏、海南卷）设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个球面上，则该球的表面积为（ ）

例5 （2009全国卷I）直三棱柱ABCA1B1C1的各顶点都在同一球面上，若AB＝AC＝AA1＝2，∠BAC＝120°，则此球的表面积等于__________.

解 如图6，设三角形ABC和A1B1C1的外心分别为O1和O2，连结O1O2，OA，O1A，取O1O2的中点O，则O到直三棱柱ABC－A1B1C1各顶点的距离都相等，即球心即为O，由余弦定理知，BC2＝AB2＋AC2－2AB·AC·cos∠BAC＝12，

即BC＝ 2，设△ABC外接圆的半径为r，则由正弦定理，得

∴S球＝4πR2＝4π×（）2＝20π.

评注 因为三角形的外心到三角形三个顶点的距离相等，所以过三角形的外心且垂直于此三角形所在平面的垂线上的任意一点到此三角形三个顶点距离也相等，所以过该三角形三个顶点的球的球心必在垂线上.

3 利用正方体或长方体的中心找球心

例6 （2012辽宁卷）已知正三棱锥PABC，点P，A，B，C都在半径为的球面上，若PA，PB，PC两两相互垂直，则球心到截面ABC的距离为__________.

解 把正三棱锥补成正方体，如图7，则球心O就是正方体的中心，

∴正方体的体对角线l等于球的直径，∴l＝，又∵面ABC把正方体的体对角线三等分，设球的半径为R，则球心O到截面ABC的距离d＝R－l＝

例7已知S，A，B，C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA＝AB＝ 1，BC＝，则球O的表面积等于（ ）

A.4π B.3π C.2π D.π

解 把四面体SABC补成长方体，如图8，则球心O是长方体的中心，∵长方体的体对角线长等于球的直径，设球的半径为R，

∴ （2R）2＝12＋12＋）2，∴R＝1，

∴S球＝4πR2＝4π.

例8 在三棱锥A－BCD中，AB＝CD＝a，AC＝BD＝b，AD＝BC＝c，则该三棱锥的外接球的表面积为 .

评注 因为正方体或长方体的中心到各顶点的距离相等，所以过正方体或长方体若干个顶点的球的球心就是正方体或长方体的中心，此类问题找球心往往需要对几何体进行补形.