对一道高考填空题的探究

安徽省枞阳县会宫中学 王怀明 （邮编：246740）

题 （2013年课标Ⅰ理数，16）若函数f（x）＝ （1－x2）（x2＋ax＋b）的图象关于直线x＝－2对称，则f（x）的最大值为________.

解法1 易知点（1，0），（－1，0）在f（x）的图象上，因为f（x）的图象关于直线x＝－2对称，

解得a＝8，b＝15.

1 解法探究

令f′（x）＝0，得x＝－2或x＝－2－或x＝－2 ＋；

令f′（x）＞0得x＜－2 －或－2＜x＜－2 ＋，令f′（x）＜0得－2 －＜x＜－2或x＞－2 ＋.所以当x＝ －2 －时，f（x）的极大值为16，当x＝－2＋时，f（x）的极大值为16.结合f（x）的图象可得f（x）的最大值为16.

还可以如下求f（x）的最大值：

另解f（x）＝ （1－x2）（x2＋8x＋15）＝－（x2＋4x＋3）（x2＋4x－5）.令t＝x2＋4x，则t＝ （x＋2）2－4≥－4，f（x）＝－（t＋3）（t－5）＝16－（t－1）2，当t＝1时f（x）取最大值为16.

解法2 易知函数f（x）＝（1－x2）（x2＋ax＋b）两个零点为－1、1，因f（x）的图象关于直线x＝－2对称，所以－5，－3是函数f（x）两个零点.即方程x2＋ax＋b＝0的两根为－5，－3.由根与系数关系得a＝8，b＝15.下同解法1，略.

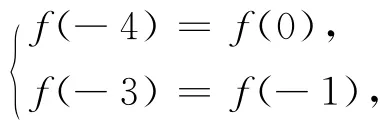
解得a＝8，b＝15得f（x）＝ （1－x2）（x2＋8x＋15），下同解法1，略.

解法4 由f（x）的图象关于x＝－2对称，得

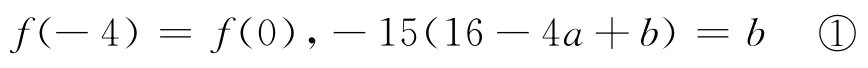
又由x＝－2是f（x）的极值点，得

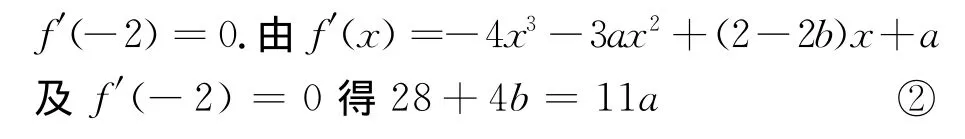
由①②解得a＝8，b＝15.

下同解法1，略.

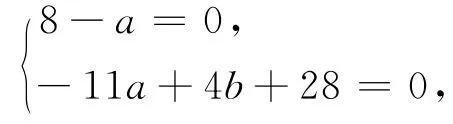
下同解法1，略.

解法6 由f（x）的图象关于直线x＝－2对称，则f（x）＝f（－4－x），

又f（x）＝ （1－x2）（x2＋ax＋b），

下同解法1，略.

2 一般性探究

这道高考题涉及一元四次函数图象关于直线对称的问题，对于一般的四次函数f（x）＝ax4＋bx3＋cx2＋dx＋e（a≠0），是否都是轴对称图形？下面进行一般性讨论.

设f（x）的图象关于直线x＝m对称，则f（x）＝f（2m－x），

由上面探究过程可知，并非所有的一元四次函数图象都是轴对称图形，必须满足一定条件，由此，我们得到如下定理：

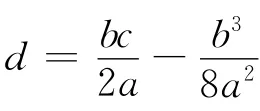
下面利用该定理解这道高考题.