对几何直观教学的若干思考

河北省晋州市实验中学 苑建广 （邮编：052260）

《全日制义务教育数学课程标准（2011年版）》指出：“几何直观主要是指利用图形描述和分析问题.借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果.几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用”，数学教学要“重视直观，处理好直观与抽象的关系”.多年的教学实践，对几何直观教学有些许感悟，今作梳理，希能对同仁有所启示.

1 几何直观的内涵分析

“几何直观”是以图形和直观符号为活动要件，以直观化的信息加工过程为形态的一种认知方式，能给数学探究提供有益、有趣的启示，在数学活动中常常起着关键作用.学生形成和使用几何直观是有水平和层次差异的.

层次Ⅰ 建立和形成敏捷准确的几何直觉——感觉与图形相随

在这一层次，几何直观能力表现在开始形成和使用数学概念、法则、问题的几何表征或图表的过程，呈现出以下特征：

（2）能根据需要画出图形，辅助思考.作图是建立直观形象的思维支柱.能根据几何或自然语言想象并画出图形，通过视觉或操作图形构成要素（线与角），感知图形的结构、位置关系、数量关系与几何特征，形成印象，进行分类，使头脑内的形象与外在可感觉到的物体建立有力连接.直观推理是几何直观的精髓，其基本要素是直观判断.我国古代数学家赵爽采用构造双图的方法，“看（证明）”出了勾股定理.几何直观虽然以直接观察为基础得到结论，但并不是无意识的，在视觉结构中的见解和推理思考一样可靠.

（3）能结合实际完善图形，发现思路.在视觉与分析的基础上，反思、抽象、调整并逐渐完善成包含众多要素及其结构关系的几何模型，这种模型往往是深度“压缩”的结果，能在应用时通过其中的部分成分快速触发其它成分，分离或完善出相关模型，整体的发现、分析与思考问题，实现图形推理.

通常一个图形都是由几个基本的子图形组成的.解题的关键是依赖视觉直观把其中关键的子结构区分出来.观察图形和分离子结构时，不需要明显的知识（定义、定理），其中包含了视觉理解和推理.视觉导致了观察方向和重心的变化.

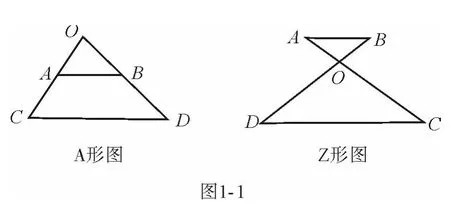
案例1 在相似形的学习中，常遇到图1－1所示两个基本图形（结合其形状特征分别命名为“A形图”和“Z形图”），用来解决“线段之比”问题.

问题 （2013年河北·晋州一模）如图1－2所示，△ABC中，AD∶DC＝1∶3，E为BD的中点，AE的延长线交BC于F.求BF∶FC的值.

分析 观察题、图特征，由于BF∶FC是同一直线上的两线段之比，可考虑过A、B、C、D、E、F这些点作平行线，完善出上述基本图，从而使问题顺利获解.

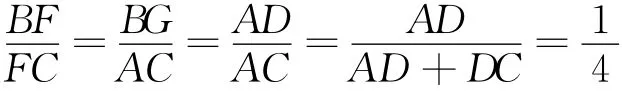
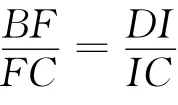
点评 法1完善并分离出两个“A形图”，法2完善并分离出两个“Z形图”，法3完善并分离出一个“A形图”和一个“Z形图”.几何直观的视觉选择与推理功不可没.

案例2 （2013年江西·南昌中考）某数学活动小组在作三角形拓展图形与研究时，经历了如下过程：

操作发现

在等腰△ABC中，AB＝AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2－1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是________

①AF＝AG＝AB； ②MD＝ME；

③整个图形是轴对称图形； ④∠DAB＝∠DMB.

数学思考

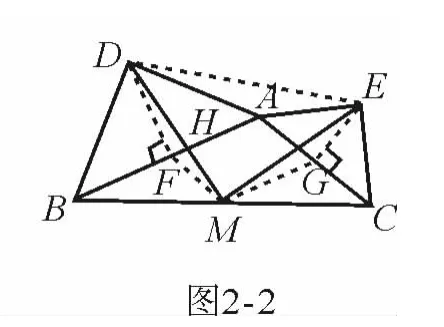
在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2－2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量和位置关系？请给出证明过程.

类比探索

在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图2－3所示，M是BC的中点，连接MD和ME， 试 判 断 △MED的形状.

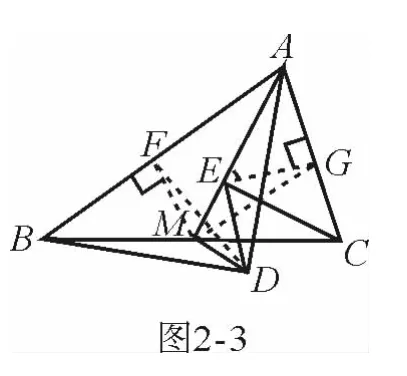
分析 常规思路自然是按部就班，依次完成题目设问，且通常是分别对MD和ME的数量关系和位置关系予以说明.换一个路子，从视觉上看，探究“MD和ME的数量和位置关系”相当于探究“△DME的形状”，而看上去 △DME象是“等腰直角三角形”，若能证出“∠MDE＝∠MED＝45°”，则问题得以突破.

如图2－2，取AB、AC的中点F、G，连结DF、FM、EG、GM、DE.由于∠FDA＝∠GEA＝45°，于是转为证 ∠ADE＝ ∠FDM，∠AED＝∠GEM.设AB＝2a，AC＝2b，易得MG＝DF＝a，MF＝EG＝b，AD＝，AE＝，于是.又易证∠DAE＝270°－∠BAC＝（180°－∠BAC）＋90°＝∠AFM＋∠AFD＝∠DFM，于是△DAE∽ △DFM，故 ∠ADE＝ ∠FDM.同理可证∠AED＝∠GEM.到此，思路被打通.将条件作此深化，则第（1）问自然得证.

将之迁移到图2－3中，易知 ∠FDA＝∠GEA＝45°，于是转为证 ∠ADE＝ ∠FDM，∠AED＝∠GEM.仍设AB＝2a，AC＝2b，可得MG＝DF＝a，MF＝EG＝b，AD＝，AE＝，于是.又易证∠DAE＝（∠DAB＋∠EAC）－ ∠BAC＝90°－ ∠BAC＝90°－∠MFB＝ ∠DFM，于是 △DAE∽ △DFM，故∠ADE＝∠FDM.同理可证∠AED＝∠GEM.思路再次被打通.

点评 如此处理，显然超出了命题人所料，是极具创新味道的.其中到处都是角和线段关系的转化，能够顺利打开思路完全是运用几何直观的结果，图形推理的价值由此可见一斑.

层次Ⅱ 实施和进行深入灵活的几何探索——视觉与思维共行

此时，几何直观活动过程已经从以视觉直观水平为主上升到“图形－分析”水平，表现出以下特征：

（1）能结合图形特征思考，具备良好的观察力.“观察”，观为看，察为思.能通过几何图形性质，即图形的组成部分和这些组成部分之间的关系，结合图形外在结构特征，来感知（视觉－几何直观成分）和分析（思维－逻辑推理成分）图形.

（2）能灵活进行合情推理，具备良好的探索力.透过观察所得，发现图形的构造特征，在外部操作或头脑中操作的支持下，对图形进行改造、变化或重组，如发现图形是否能在一定程度上动态变化，设计图形变化过程中的特殊情形，测量、比较图形，进而猜测和归纳图形的性质，探索问题，发现结论.其特征是在视觉的基础上，进行模拟和猜想.

（3）能因题制宜构造分析，具备一定的创造力.能够在心理上操作、旋转、翻折或逆转几何对象，并能感受和想象操作过程中元素之间的数量与位置关系的变化，出现视觉的弹性与跳跃、组合与分析，既能注意把握整体，又不忽视细节，从多层面上捕捉有效信息，广泛地对比、联想，构造、完善图形，启示或产生创造性的方法.

案例3 （2013年山东·枣庄中考）从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图3所示的零件，则这个零件的表面积为________.

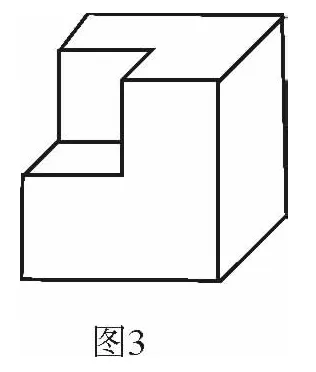
分析 整体观察图形，在头脑中借助“平移”实现对问题解决过程的优化，把求“表面积”的问题转化成求“从上、下、左、右、前、后六个方向看到的视图面积之和”的问题，则极易得到这个零件的表面积为6×（2×2）＝24.

点评 此时，视觉操作虽然没有显示到卷面上，但却成为解题的关键，甚至能将问题拓展为：只要是从毛坯的一角，挖去任意一个长方体，则其表面积均为24，是不变的.几何直观的趣味性油然而生.

案例4 （2013山东·临沂中考）如图，矩形ABCD中，∠ACB＝30°，将一块直角三角板的直角顶点P放在两对角线AC、BD的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别与边AB、BC所在的直线相交，交点分别为E、F.（1）当PE⊥AB，PF⊥BC时，如图4－1，则的值为__________；（2）现将三角板绕点P逆时针旋转α（0°＜α＜60°）角，如图4－2，求的值；（3）在（2）的基础上继续旋转，当60°＜α＜90°，且使AP∶PC＝1∶2时，如图4－3，的值是否变化？证明你的结论.

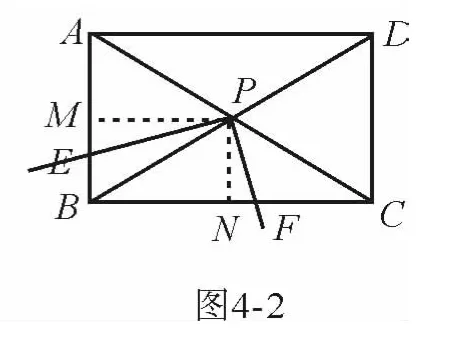
点评 此例之解决，在下笔之前，已然在头脑中完成了对图形的操作与转化，预测到继续实施程序操作成功的可能性.几何直观先行于书写中的推理与表达.

层次Ⅲ 成为分析解决问题的有效工具——抽象与形象互辅

透过物理世界和直观经验建构几何图形，联系性质、概念、定理，达到几何直观的运用已达成熟阶段：

（1）有效分离出具有特殊性质或熟悉的基本图形，突破问题.

（2）善于构造几何模型，变更命题.

（3）能够全面认知图形，随机应变.对图形已经形成动态观察和理解的习惯，头脑中操作的是一般化图形，以及相应的元素和结果后面隐藏的结构和关系.

案例5 （2013年江苏·连云港中考）小明在一次数学兴趣小组活动中，对一个数学问题作如下探究：

问题情境 如图5－1，四边形ABCD中，AD∥BC，点E为DC边的中点，连结AE并延长交BC的延长线于点F.求证：S四边形ABCD＝S△ABF.（S表示面积）

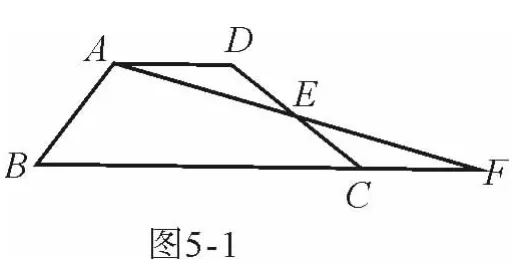
问题迁移 如图5－2，在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN，分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现，△MON的面积存在最小值.请问当直线MN在什么位置时，△MON的面积最小，并说明理由.

实际应用 如图5－3，若在道路OA、OB之间有一村庄Q发生疫情，防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON.若测得∠AOB＝66°，∠POB＝30°，OP＝4km，试求 △MON的面积.（精确到0.1km2.参考数据：sin66°≈0.91，tan66°≈2.25≈1.73）

拓展延伸 在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）、（6，3）、（，）、（4，2），过点P的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形的面积的最大值.

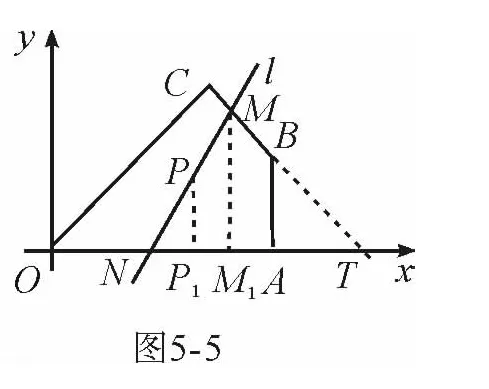
分析 题目呈现出明显的从模型逐步推向应用的构题模式，能否在视觉和心理上发现和完成对图形的调整、完善，并化归为模型是解题的关键.图5－1对应问题情境即是本题的模型，容易完成证明.图5－2中，当P为MN中点时，S△MON最小.思路即是化归为模型：过点P作另外一条直线EF交OA、OB于点E、F，不妨设PE＞PF，过点M作MG∥OB交EF于G.由“模型”知，当P为MN中点时，S△MON＝S四边形MOFG，由于S△EOF＞S四边形MOFG，所以S△EOF＞S△MON，即当P为MN中点时，S△MON最小.此时，图5－2成为新的模型，将之迁移到图5－3中，可知当PM＝PN时，△MON符合要求，进而结合所给数据，借助图中辅助线，利用三角形中位线性质得S△MON值.“拓展延伸”应分作两种情形考虑：①如图5－4，完善图形，当PM＝PN时，S△DMN最小，此时S四边形OANM最大，结合所给数据，利用三角形中位线性质，可得其值为10；②如图5－5，完善图形，当PM＝PN时，S△TMN最小，此时S四边形OCMN最大，结合所给数据，先得直线BC解析式、点T坐标、S△TOC值；结合点P的坐标，利用三角形中位线性质，可得点M坐标，进而可得S四边形OCMN＝8.25，故截得四边形面积的最大值为10.

点评 视觉的灵活性和敏捷性是顺利实现化归为模型的前提.

2 几何直观的教学建议

结合几何直观能力的形成过程和运用特点，提出以下教学建议：

（1）在内容学习方面，要发展几何直观能力，教学时应借助实物或图形，直观引入几何概念和深化对几何命题的理解.通过设计有效的变式练习，形成对线、角等几何基本要素的“（位置和数量）关系感”，以及对图形空间形状和大小的感觉，这是建立几何直观、形成几何意象的基础.通过动手或心智操作，借助实物或图形直观，在视觉认知的基础上，加强图形和语言符号的联系，活化命题理解，深化命题的纵横联系，形成命题网络，完善心理图式.对于一些具有数、形双重身份特征的概念，更要注重揭示数和形的联系，互辅互释，双向升华，把几何直观和数式精确的特征融合到对研究对象的理解之中.

（2）在知识运用方面，要发展几何直观能力，教学时应帮助学生树立运用几何直观的意识，养成借助图形推理的习惯.生动的几何推理往往关系到公式和符号后面的意义.几何直观以直觉、想象和现实经验为基础，为了描述和交流信息的需要，为思考和形成新观念的需要，为深入理解的需要，在头脑中，或在纸上，或利用技术工具，绘出并解释图形、图象和图表，其中伴随着能力的发展.通过有意设计，如利用折纸、动手操作几何对象、几何画板演示等手段，让学生经历从有意识地感受与运用，到自觉运用，再到自动化运用几何直观理解与解决数学问题的过程，从外部操作逐渐过渡到心智操作，几何直观意识才能逐步树立起来，并内化为个体进行数学活动的一种品质或习惯，如善于借助几何图形把抽象的问题直观化；善于发现图形中的结构特征，从中抽取出数量、形状、位置、变换等关系；产生“完善图形”的冲动，分割、补充图形，使之呈现出“标准”或“熟悉”的状态，猜想出一般结论，实现合情推理到演绎推理的自然过渡；鼓励创新，从多角度感知、认识和分析图形，获得独特见解.在此过程中，要注意由几何直观引发的想当然型失误：

案例6 求证：所有的三角形都是等腰三角形.

且看证明过程：如图6，△ABC是任一三角形.作∠A的平分线AO与BC的中垂线OH（垂足为H）相交于点O；过点O作OM⊥AB于M，ON⊥AC于N；连结OB、OC，易 知 ∠OAM＝∠OAN，∠OMA＝ ∠ONA＝ 90°，OM＝ON， 则△OAM≌ △OAN，于是有AM＝AN；由OH为BC的中垂线，得OB＝OC，结合OM＝ON，可得Rt△OMB≌Rt△ONC，则MB＝NC；继而可得，AM＋MB＝AN＋NC，即AB＝AC.

点评 如此荒谬的结论和看似毫无漏洞的证明过程，形成鲜明的对比.问题在哪里？如果作图准确的话，点O应在△ABC外！这一点提醒我们，借助几何直观解决问题，要避免想当然的视觉判断，随意地构造本不存在的图形.

（3）从教学评价方面看，要发展几何直观能力，应改进评价方法，实施多元评价.在进行命题设计时，要图文并茂，形（形象）神（抽象）兼备，增加题目的视觉操作成分考查.在评价方法上，可增加过程考查，如进行“出声”地思考，表达解决几何问题时观察与分析的过程：哪些是看（依赖几何直观）出来的？哪些是分析（依赖逻辑推演）出来的？用到哪些图形调整与变换的策略（如把试卷转动一个角度，或翻过来看试卷的背面，以找到容易观察或熟悉的角度）.再如，给予操作工具或物体，如剪刀、纸片、正方体块等，允许进行裁剪、拼接、垒砌等实际动手操作活动，或运用信息技术手段，如几何画板等来理解和解决问题，带来互动性和动态性的体验，享受数学活动的愉悦感，动员非智力因素的参加.

1 中华人民共和国教育部制定.全日制义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2011

2 苑建广.信息转化 —— 问题解决的核心策略［J］.中国数学教育（初中版），2012.3