一种沙漠场景地杂波雷达散射截面的仿真方法

李建军，于利娟，刘 璇

(西安电子科技大学理学院，陕西西安 710071)

地基雷达对低空及超低空目标进行探测时，地杂波反射率对低空及超低空目标的检测性能具有重要影响。目标的雷达散射截面(Radar Cross Section，RCS)是表征雷达目标对于照射电磁波散射能力的物理量［1］。当雷达波束照射在地面时，地面反射电磁波的能力通常用地杂波雷达截面积表示。除此之外，场景雷达截面积的研究在雷达系统设计、合成孔径雷达(Synthetic Aperture Radar，SAR)成像和雷达信号仿真中具有重要意义。

一般情况下，当雷达波照射沙地时，散射场既有沙地表面散射场，也有透射波束与沙层沙颗粒相互作用的体散射场。由于干沙物质较小的介电常数，沙物质的体散射相对于表面散射可以忽略不计［2］。因此这里只考虑沙漠场景的表面散射，同时完全忽略多重散射。

文中首先介绍了沙漠沙丘场景的物理特性;其次对沙漠场景的数字高层模型(Digital Elevation Model，DEM)数据进行插值处理;然后计算三角形小平面的面积、法矢量、局部入射角等几何参数;再次判断局部入射角，确定后向散射系数模型;最后求每个三角形小平面的RCS，每一个三角形小平面的RCS排列是根据沙漠场景DEM数据的排列顺序排布的，由此即可得到沙漠场景的RCS矩阵。

1 沙漠场景表面物理特性及几何建模

1.1 沙漠沙丘表面物理特性

沙颗粒一般被认为是直径在0.062 5～2.0 mm之间的粒子，大量沙颗粒与粘土的混合组成了沙漠。这些沙颗粒与黏土的混合物在风的作用下，形成了多样的沙漠地貌。一些沙漠区表现为较平坦的沙层，有些沙层在风的作用下形成了小尺度的沙波纹，在顺风方向上，这些波纹具有波长1～25 cm，幅度0.2～5 cm的特征。沙漠典型的表现形式是沙丘，这些沙丘在盛行风的作用下，波长一般 3～600 m，幅度在 0.1～100 m间［3］。

沙漠表面的粗糙程度一般用均方根高度和相关长度l描述，当ks＜0.5时沙表面为光滑表面，当0.5＜ks＜1时认为略粗糙表面，当ks＞1时为粗糙表面，其中k为电磁波波数。

实验表明，当频率在0.245～6 GHz之间时沙物质的介电常数实部随频率几乎为常数，值约为2.6，而虚部随频率的增大而单调减小，频率为0.25 GHz时为0.13，当频率接近 6 GHz时，虚部减小到 0.012［4］。

1.2 DEM插值处理及沙漠场景表面几何建模

DEM数据是对地形地貌的一种数字建模。SRTM数据每个文件记录一个地表经纬方格数据，版本有SRTM1和SRTM3，精度分别为30 m和90 m。因为场景的DEM数据通常是按照一定的空间采样间隔进行勘测获得，采样步长远大于雷达分辨单元的尺寸，所以必须对原始DEM数据进行插值处理得到即保持地面场景随机起伏特征又满足计算条件的精细DEM数据。图1(a)表示插值前的场景模型，图1(b)为插值后的沙漠场景模型。

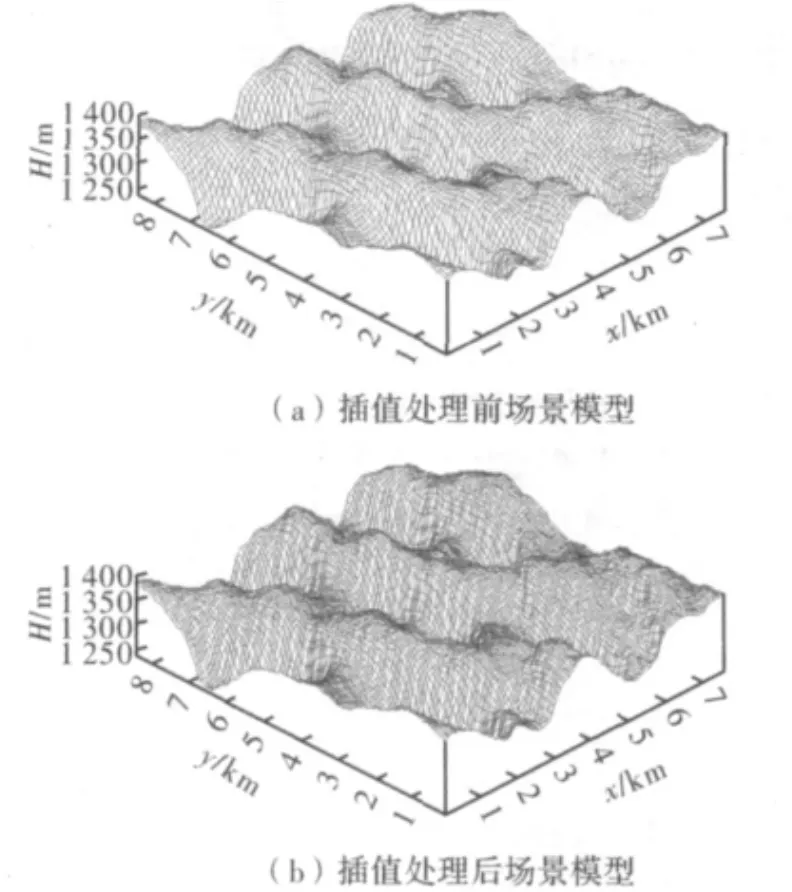
图1 插值处理前后沙漠场景模型对比

2 三角形小平面模型

沙丘表面特殊的起伏特性，可以选择大量与沙丘表面相切的小平面来近似描述，沙丘表面的电磁散射特性为所有小平面电磁散射相干叠加的结果。小平面的尺度应该足够小，以便更好地接近地表起伏，但需大于入射波波长。

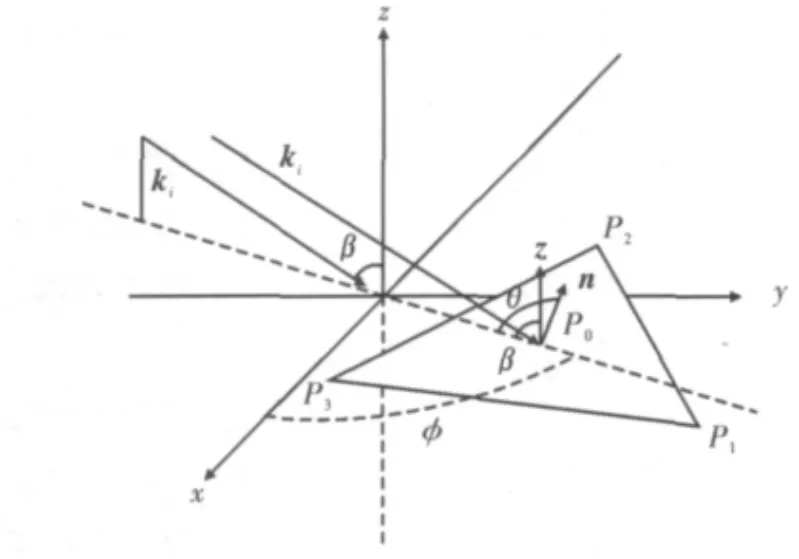
图2 三角形小平面单元模型

三角形小平面模型如图2所示，P1，P2和P3表示三角形小平面的3个顶点，P0为该三角形平面的重心。图2中，θ为局部入射角;β为入射波与z方向的夹角;n为三角形平面的单位法矢量;ki为入射波矢量;P1点的坐标为(xp1，yp1);高程为zp1;P2点的坐标为(xp2，yp2);高程为zp2;P3点的坐标为(xp3，yp3);高程为zp3;因此三角形平面面元的单位法矢量为

三角面平面局部入射角为

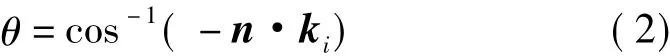
三角形小平面的空间几何参数可由式(1)和式(2)确定，表面参数由相关长度和均方根高度描述，表征平面的粗糙度。

3 角度截断后向散射系数模型

后向散射特性表明沿入射角反向辐射的那一部分反射功率，是单位面积的平均雷达截面，一般情况下，后向散射系数是入射波频率、极化、入射角、散射单元介电常数，和几何特征等的函数，同时取决于地形、地貌等诸多因素。

3.1 修正的几何光学模型

当小平面粗糙程度满足条件:4πrccos3θ·λ且(2kσcosθ)2＞10时，后向散射系数随入射角而缓慢变化，在小入射角情形下可用几何光学模型近似。在这种情况下，模型参数为均方根表面坡度m。后向散射系数可表示为［5］

式中，rc为粗糙面曲率半径;p=h，v表示水平极化或垂直极化;Rpp(0)表示垂直入射时的菲涅尔系数;σ2为粗糙面方差;ρ″(0)表示相关函数在原点的二阶导数。为得到与实验结果［3］比较吻合的结果，通过数值拟合，给式(3)添加一个修正因子

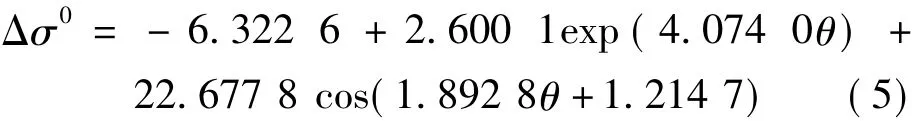
添加修正因子后的模型为

图3表示添加修正因子后的后向散射系数与实验数据的比较结果，曲线(1)为几何光学模型添加修正因子后的后向散射系数结果，曲线(2)为实验结果。比较发现，给几何光学模型添加修正因子Δσ0后能够和实验结果较好地吻合。

3.2 γ-f后向散射系数模型

一种能够反映雷达频率、入射余角和地形种类对地杂波反射率影响的的γ-f模型，γ-f模型表达式为

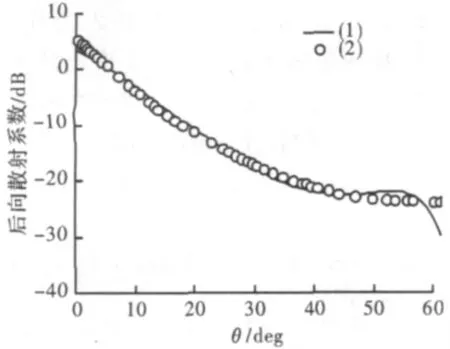
图3 修正的GO模型后向散射系数随入射角的变化曲线

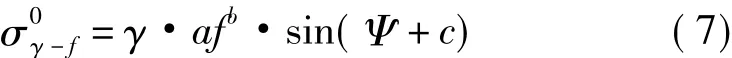
式中，f为工作频率，单位GHz;Ψ为入射余角或称擦地角。

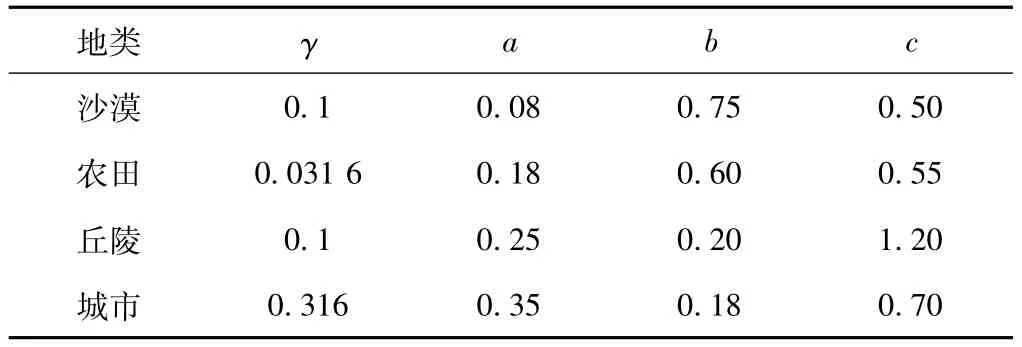
表1 各种地类条件下的相关参数

参数c的引入是为了更精确地模拟实验数据并防止在入射余角接近0°时用分贝表示的地杂波反射率急剧变为 - ∞，单位(°)。a、b、c、γ 均为基于统计方法得到的系数，不同地类条件下的参数如表1所示。

3.3 角度截断散射系数模型

使用一种基于局部入射角划分来选择相应的沙漠表面电磁散射计算方法的角度截断模型:局部入射角小于限定角(约60°)时，使用修正的几何光学模型计算三角形小平面的散射系数，当局部入射角大于限定角时，使用γ-f模型计算三角形小平面的散射系数。最后混合模型可表示为

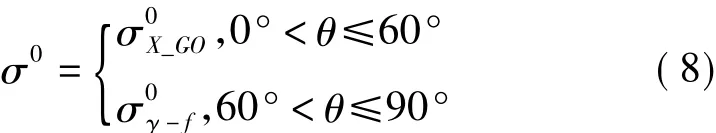
4 求解RCS矩阵

考虑到DEM数据插值处理后得到的三角形面元尺寸相对较小，因此以每个三角形平面单元重心处的后向散射系数求取该单元的RCS，地杂波雷达截面积的确定包括后向散射系数和散射单元面积ΔS两个因素，散射单元的雷达截面积为［6］

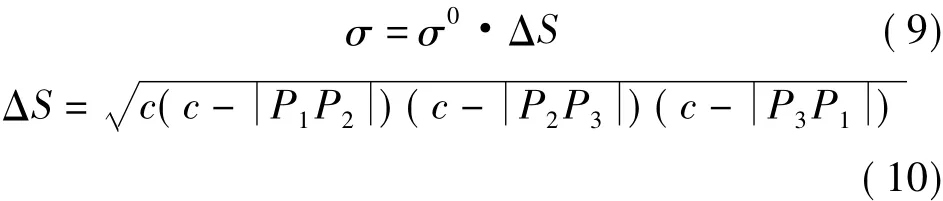
其中，c=/2.0，ΔS为三角形平面的面积，式中σ0为该三角形平面的平均后向散射系数，计算出每个三角形面元的平均后向散射系数，即可得到整个沙漠场景的后向散射系数图。对每个三角形平面作RCS，即可得到沙漠场景的RCS矩阵。RCS矩阵根据沙漠场景的DEM数据排布，每个三角形平面单元在尺寸上就是一个RCS单元［7］。

5 实验结果

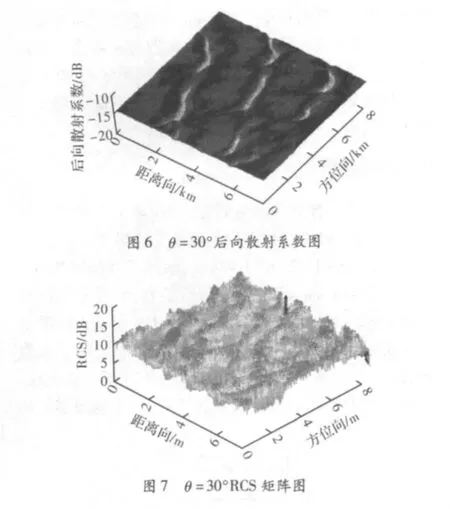
为检验计算方法的有效性，利用航天飞机雷达地形测绘使命(SRTM)发布的新疆塔克拉玛干沙漠DEM数据(高程范围1 235～1 434 m，数据采样间隔90 m，场景大小7.5 km×8.3 km)进行仿真，沙物质介电常数取ε=2.71+i0.023，频率取14 GHz，仿真方框图如图4所示。图5为DEM模型，图6为后向散射系数图，图7为RCS矩阵图。将图6、图7与图5做比较，沙漠场景面元的后向散射系数、RCS大小能与实际场景起伏一致。

6 结束语

从微积分的思想出发，利用小平面模型与数字高程模型数据用于获得RCS矩阵的方法，计算出各个小平面单元的RCS，从而得到沙漠场景表面RCS图，该方法得到的RCS矩阵图能够基本反应出沙漠场景沙丘周期性起伏的特性。从而表明该方法在模拟真实环境下沙漠场景雷达散射截面是可行的。

［1］黄培康，殷红成，许小剑.雷达目标特性［M］.北京:电子工业出版社，2005.

［2］ADIB Y N，KAMAL S，FAHAD A A，et al.Characterization of radar backscatter response of sand-covered surfaces at millimeter-wave frequencies［J］.IEEE Transactions on Geoscience and Remote Sensing，2012，50(6):2345-2354.

［3］HAROON S，DAVID G L.Microwave backscatter modeling of erg surfaces in the sahara desert［J］.IEEE Transactions on Geoscien-ce and Remote Sensing，2005，43(2):238-247.

［4］CHRISTIAN M A.Microwave permittivity of dry sand［J］.IEEE Transactions on Geoscience and Remote Sensing，1998，36(1):317-319.

［5］ULAB Y，KOUYATE F，FUNG K，et al.A backscat-er model for a randomly perturbed periodic surface ［J］.IEEE Transactions on Geoscience and Remote Sensing，1982，GE-20(4):518-528.

［6］熊兴斌，王红，赵选峰，等.地杂波雷达截面积模型性能对比分析［J］.舰船电子对抗，2007，30(1):68-71.

［7］金玉荣，孙造宇，梁甸农.星载SAR地面场景RCS仿真［J］.现代电子技术，2007(7):15-18.