弧齿锥齿轮半滚切法切齿与滚动检验仿真

张武刚，赵栓峰，张传伟

(西安科技大学机械工程学院，西安 710054)

0 引言

弧齿锥齿轮广泛应用于航空、汽车、船舶等领域，弧齿锥齿轮的生产在机械制造中占有重要的地位。当前，国外弧齿锥齿轮的生产广泛采用CNC铣齿机并配套专家系统软件实现弧齿锥齿轮数字化设计制造［1-2］。由于进口CNC铣齿机及配套软件价格十分昂贵，国内许多中小企业仍以传统机械结构的铣齿机为主要加工设备，采用滚动检验法进行精度检查［3］。使用传统铣齿机加工弧齿锥齿轮，必须经过反复试切、修正和调试，才能得到满意的齿面啮合特性。针对这一现状，有必要研究利用计算机技术，完成切齿调整和滚动检验的仿真方法。在计算机环境下，先根据机床初始切齿调整参数加工出大小齿轮，再对大小齿轮进行滚动检验，检查齿面接触情况，根据齿面接触印迹对初始切齿参数进行调整，直到获得较理想齿面啮合特性和机床调整参数。利用仿真过程代替试切过程将会在一定程度上缩短机床调整时间，提高生产效率。

目前，弧齿锥齿轮切齿仿真方面的研究主要集中在真实齿面数学表达方法和啮合仿真模型构建方面。文献6利用展成法原理推导弧齿锥齿轮球面渐开线方程，利用Pro/E软件，建立了精确弧齿锥齿轮模型。文献7利用NURBS对齿面理论计算点进行拟合，以此为基础，建立数字化齿面仿真模型，然后进行齿面接触分析，获得啮合路径和传动误差。文献8利用展成法原理，模拟实际加工过程，建立数学模型，计算在设定运动时间间隔内相邻两次铣齿刀刃直线交点坐标，并以此作为齿面点，进而在Pro/E软件中进行重构，然后进行切齿仿真。目前的研究中，齿面点计算部分多涉及较复杂的矩阵运算过程，数学处理需借助专门软件进行。计算得到齿面点数据后，一般又需要切换到其他软件平台下构建仿真模型进行切齿仿真。这会给技术应用带来不便。

本文以格里森制弧齿锥齿轮半滚切法切齿原理和实际切齿过程为依据，探讨在单一软件平台下，避免复杂数学计算和多软件平台的切换，实现切齿和滚动检验仿真过程，即基于NX软件平台的半滚切法切齿和滚动检验仿真实现方法。

1 半滚切法切齿原理

传统格里森机械结构弧齿锥齿轮铣齿机由安装在摇台上的铣刀盘旋转进行铣齿，当工件和摇台机构(模拟产形轮)以一定的传动比绕各自的轴线旋转时，刀盘就会在工件轮坯上切出一个齿槽。齿轮的切削过程就像一对准双曲面齿轮的啮合过程。半滚切法铣齿主要针对传动比≥3，大轮节锥角≥70°的弧齿锥齿轮的大批量生产。半滚切法中先用成型法进行大轮的加工，再用刀倾法或变性法进行小轮的加工。本文中，小轮采用带有刀倾机构的铣齿机(即刀倾法)进行切齿。

1.1 大轮成型法切齿原理

成型法加工大轮的过程中摇台不动，仅刀具绕其自身轴线旋转，大轮轮坯相对其回转轴线和摇台是静止的。当刀具切入到全齿深后迅速退出齿槽，轮坯分度后，再进行另一齿槽的加工，大轮齿面曲率与刀盘的齿面曲率是完全相同的。

1.2 小轮刀倾法切齿原理

切制小轮时，粗加工采用滚切法，即由双面刀盘一次完成齿槽两面的粗切。精加工采用刀倾法，使用单面刀盘分别加工小轮凹凸两面，并进行齿面修正［4］。图1为刀倾法精加工小轮的切齿坐标系。其中，SM为机床中心坐标系，其原点为机床平面与产形轮轴线的交点;SW为工件坐标系，其原点为轮坯顶点;ST为刀盘坐标系，其原点为刀盘轴线与刀尖平面的交点;刀倾法加工小轮有九个基本的机床调整参数［5］，E01为垂直轮位;S1为径向刀位;q1为角向刀位;δM1为轮坯安装角;X1为轴向轮位修正值;XB1为床位;i为刀倾角;j为刀转角;i01为滚比。S1、q1、i、j四个参数用来确定刀盘相对于产形轮的位置，E01、δM1、X1、XB1四个参数用来确定小轮轮坯相对于产形轮的位置。

图1 刀倾法小轮切齿调整坐标系示意图

2 切齿仿真

使用半滚切法切齿，由于大轮成型法加工原理较为简单，限于篇幅，不做讨论。下文着重探讨刀倾法小轮切齿仿真方法。为使仿真结果准确、可靠，切齿仿真过程必须按照实际铣齿机调整和切齿过程进行。这样，仿真所得齿轮几何模型和实际加工出的齿轮才能保持很好的一致。

2.1 切齿仿真流程

在NX软件平台下，依据半滚切法切齿原理、机床调整和切齿过程，刀倾法小轮切齿仿真方法流程如图2所示。

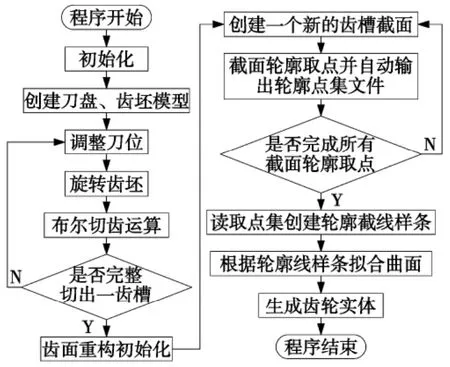
图2 刀倾法小轮切齿仿真方法流程

切齿仿真过程分为两部分，即齿面加工和齿面重构。齿面加工时，首先要根据格里森SFT计算卡进行切齿计算，得到切齿过程所必须的机床调整参数、刀盘几何参数和轮坯几何参数;第二，根据切齿调整坐标系示意图建立机床、轮坯和刀具坐标系，确定各自几何位置;第三，分别在刀盘和轮坯坐标系下建立刀盘和轮坯实体模型;第四，调整刀盘和轮坯位置，即利用NX软件二次开发工具驱动刀盘和轮坯实体，使其模拟一对准双曲面齿轮进行啮合运动，并将啮合过程离散化，分成若干步进行，每一步结束时，使轮坯和刀盘实体进行布尔减运算，从而在轮坯上切下一层材料，直到逐步、逐层切完一个齿槽全部多余材料为止，完成一个齿槽的加工。

由于齿槽是刀盘和轮坯经过若干步逐层加工出来的，所以仿真得到的齿槽曲面受离散步数的影响，步数越多，齿面越光滑。为提高齿面仿真精度，要对其进行重构。齿面重构时，首先在齿面适当位置做若干截面截取齿槽轮廓;第二，用NX软件二次开发工具遍历各截面，求各截面与齿槽轮廓相交所得截线节点数据，并将其输出保存成数据点文件;第三，在新建部件中读取已生成的节点数据文件，创建各截面截线样条曲线，再由各截线样条曲线拟合出齿槽曲面，直到构建出小轮整体模型。至此切齿仿真过程结束。

2.2 切齿仿真实例

本文以表1列出的一对弧齿锥齿轮为例，使用上述半滚切法切齿仿真方法，进行模拟铣齿。根据格里森SFT计算卡得到的小轮切齿刀盘和机床调整参数见表2，由以上参数可在NX软件下建立刀倾法小轮切齿仿真模型。

表1 轮坯参数

表2 小轮切齿刀盘和机床调整参数

在切齿程序的驱动下，产形轮与轮坯分若干步进行啮合运动，每转一步，刀盘即在轮坯上切下一层材料，直到切出一个完整齿槽，然后在轮坯齿面宽度方向取六个锥形截面，在径向取四个锥形截面，如图3所示。再利用取点程序自动生成各截面上齿槽轮廓的节点坐标文件。

如图4所示，根据各截面节点坐标创建出齿槽轮廓样条曲线，再如图5所示，由轮廓样条曲线拟合出齿槽曲面。然后根据单个齿槽曲面可进一步得到整个刀倾法加工出的小齿轮实体模型。

图3 切出单个齿槽

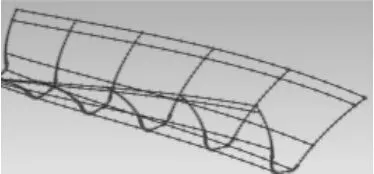
图4 齿槽轮廓截线样条网格

图5 拟合出的齿槽曲面

由上述切齿仿真方法所建立的大小齿轮模型如图6所示。

图6 大齿轮和小齿轮模型

3 滚动检验

建立了半滚切法大小齿轮几何模型后，可借助NX软件的运动仿真模块通过模拟大小齿轮传动过程进行齿面的滚动检验，检查大小齿轮传动过程中齿面接触印迹。方法如下：先建立锥齿轮装配模型，然后进入软件的运动仿真模块，设置小轮和大轮传动的基本参数，接下来定义齿轮副的基本参数，如传动比、转速、回转中心、驱动等。然后进行运动分析，动态显示齿轮传动过程，如图7所示。

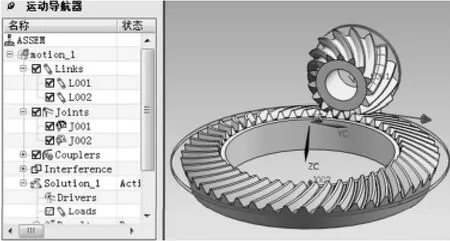
图7 大小齿轮传动运动分析

齿面接触区滚动检验通过运动过程干涉检查功能来实现，将干涉检查模式设置为“显示接触区曲线方式”来动态显示接触区滚动印迹，传动过程中滚动接触区印迹边界即可清晰地显示出来，如图8所示。

图8 滚动检验齿面接触印迹

根据接触区滚动检验结果，调整初始切齿参数，并重新进行切齿仿真和滚动检验，直到获得满意的接触区质量为止。此时的机床调整参数，即是较理想的切齿参数，可供实际加工时调整机床参考。

4 结论

传统半滚切法弧齿轮铣齿时，要得到理想的机床调整参数，往往采用试切法。使得切齿调整过程周期长、成本高、效率低。采用本文所述的仿真方法，可在计算机上完成试切调整和齿面滚动印迹检查，能在一定程度上检验切齿参数的合理性。相对于其他切齿仿真方法，该方法在单一软件平台NX软件下完成，避免了复杂数学计算和多软件工具的切换问题，具有流程简单、速度快的优点。作为切齿仿真过程的结果所生成的弧齿锥齿轮实体模型，与理论齿轮模型相比，更接近实际加工齿轮，可作为齿轮设计及有限元分析的理想模型，所以该仿真方法也可作为弧齿锥齿轮建模的一种新途径。

［1］樊奇让·德福.格里森专家制造系统(GEMS)开创弧齿锥齿轮及双曲面齿轮数字化制造新纪元［J］.世界制造技术与装备市场，2005(4)：87－93.

［2］Du Wanli，Zhang Zuzhi，Jia Shuang，Mao Ming.Geometric modeling of generating manufactured spiral bevel gears based on cutting simulation［J］.Transactions of Nan jing University of Aeronautics＆ Astronautics，2010(3)：239－247.

［3］李兆文，王勇，陈正洪.螺旋锥齿轮技术的研究现状［J］.工具技术，2007，41(10)：3 －6.

［4］赵世纯.弧齿锥齿轮加工工艺简介［J］.綦齿传动，2008(2)：36－43.

［5］曾韬.螺旋锥齿轮设计与加工［M］.哈尔滨：哈尔滨工业大学出版社，1989.

［6］汤兆平，孙剑萍.格利森弧齿锥齿轮的精确参数化设计与运动仿真分析［J］.机械设计与制造，2011(4)：18－20.

［7］苏进展，方宗德.弧齿锥齿轮数字化齿面啮合仿真分析与试验［J］.西北工业大学学报，2012(8)：565－569.

［8］李兆文，王勇，万金领.基于实际切齿方法的弧齿锥齿轮建模与仿真［J］.组合机床与自动化加工技术，2008(6)：26－30.

［9］Zhang Junhui，Fang Zongde，Wang Cheng.Digital Simulation of Spiral Bevel Gears＇Real Tooth Surfaces Based on Non-U-niform Rational B － Spine［J］.Journal of Aerospace Power，2009，24(7)：1672 －1676.

［10］李特文.齿轮啮合原理［M］.卢贤占，高业田，王树人，译.上海：上海科学技术出版社，1984.

［11］王裕清，武良臣.弧齿锥齿轮接触区理论与切削过程仿真［M］.北京：煤炭工业出版社，2004.