数控机床NURBS曲线插补轮廓误差自动控制
2013-09-12马方魁
马方魁,郇 极
(北京航空航天大学机械工程及自动化学院,北京 100191)
0 引言
在 NURBS(Non-Uniform Rational B-Spline,非均匀有理 B样条)方法和STEP-NC(Standard for The Exchange of Product model data-Numerical Control)标准出现之前,各数控系统和计算机辅助设计/制造(CAD/CAM)厂商所采用的样条曲线表示方法也各不相同,存在着严重的互操作性问题。为实现数控系统与 CAD/CAM软件之间的双向数据传输,在STEP-NC中,自由曲线曲面均可由NURBS方法来表示。GE FANUC、SIEMENS等高档数控系统(如FANUC16i/18i/160i、SIEMENS840D/840Di等)均具有包括 NURBS在内的样条插补功能,UG、CATIA、MasterCAM等高档CAD/CAM软件也能直接输出NURBS刀轨文件。
相比较直线和圆弧插补,NURBS插补能大量压缩数控加工程序,减少前瞻时所需要的程序段数量和提高进给速度[1],便于实现运动精度的控制。
目前,不少学者在应用NURBS插补提高加工精度和速度方面进行了各种研究:赵国勇等[2]在考虑机床各轴联动时动态性能不一致引起的轮廓误差基础上,提出一种基于NURBS插补器的交叉耦合控制方法;潘海鸿等[3]出7段式S曲线加减速全程规划的NURBS曲线自适应分段插补算法。
目前,高速加工并没有统一、确定的定义,一般情况下指以高于传统加工5~10倍的加工速度进行切削加工。除了采用转速尽可能高的主轴,数控系统应能实时根据被加工零件的刀具轨迹选择最佳的进给速度,在允许的误差范围内以尽可能高的加工进给速度产生位置指令。高速加工数控系统中,伺服滞后引起的误差是影响加工精度的主要因素[4]。为减少由伺服滞后引起的轮廓误差,必须加入一定的控制策略[5]。本文在研究圆弧插补径向轮廓误差的基础上,提出了一种NURBS曲线插补轮廓误差自动控制算法,并根据给定的轮廓误差对算法进行了仿真,得出了仿真结果。
1 圆弧插补轮廓误差分析
高速数控机床一般采用交流同步电机或直线电机驱动。其伺服系统数学模型的传递函数可简化如下[6]:

其中,典型中、小型数控机床的控制参数为:频响ωn=80~150s-1,阻尼系数 ξ=0.8 ~0.9,位置增益KV=15 ~30s-1。
当采用圆弧插补时,X、Y两轴的输入指令为:
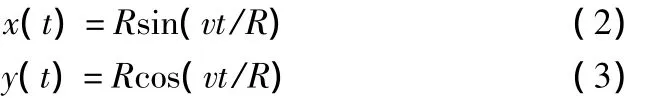
其中,R为圆弧半径,v为实际进给速率,x(t)、y(t)为在进给时刻t时的X、Y轴坐标。
数控机床中,多轴同时运动进行工件轮廓加工时,各轴的运动误差将直接反映到所加工的曲线轮廓上,形成轮廓误差。定义轮廓误差为:刀具实际位置与指令位置在指令轨迹法线方向上的偏差。
在自动控制原理中,对控制系统的快速性及稳态性等问题进行分析时常采用频率法。对闭环伺服系统模型进行幅频特性分析,则由式(1)、式(2)和式(3)可得,在圆弧插补时数控机床轮廓误差er与进给速率v间的关系可由式(4)求出[7]。

由于伺服系统运动误差的影响,数控机床采用逆时针圆弧插补时的指令轨迹与实际轨迹如图1所示。其中,R和R实分别为指令轮廓曲率半径和实际轮廓曲率半径,可以看出,实际轨迹曲线为梨形。

图1 圆弧插补指令轨迹与实际轨迹
对于常用数控机床控制参数,取阻尼系数ξ=0.8、位置增益KV=0.2ωn或0.3ωn,以角速度v/R为横坐标、er/R为纵坐标(为双对数坐标系),则分别在频响 ωn=80s-1、120s-1和 200s-1时的曲线如图 2、3所示,在此坐标系下的轮廓误差曲线近似为直线。
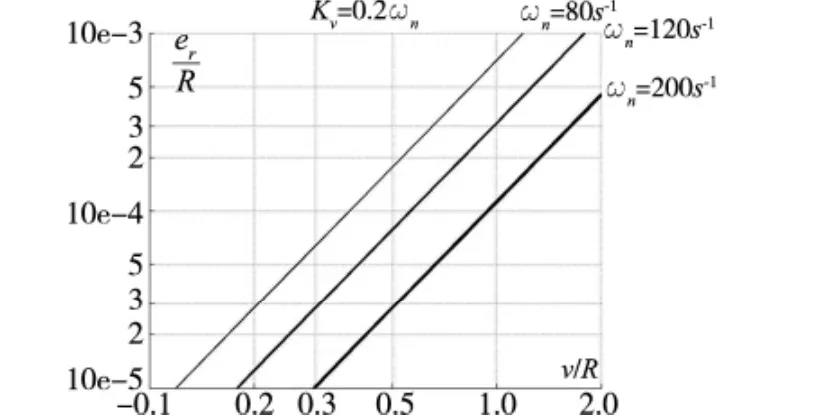
图2 圆弧插补轮廓误差曲线(KV=0.2ωn)

图3 圆弧插补轮廓误差曲线(KV=0.3ωn)
2 NURBS曲线插补轮廓误差控制
2.1 NURBS曲线定义
NURBS采用控制顶点(di)、节点矢量(ui)及权因子(ωi)来定义自由曲线,一条k次NURBS曲线可以表示为一分段有理多项式的矢函数:
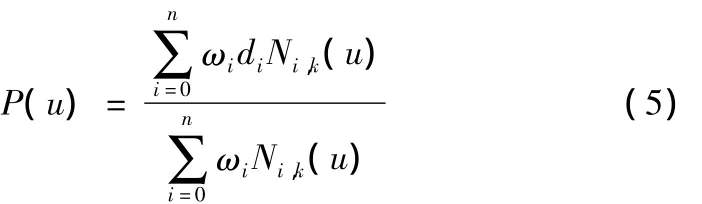
其中,n为控制顶点个数,参数u∈[uk,un+1],Ni,k(u)是由节点矢量U=[u0,u1,…,un+k+1]按照德布尔 -考克斯递推公式进行定义:

数控加工中一般NURBS次数一般取为3。
2.2 NURBS曲线曲率半径计算
根据微分几何知识可知,对于式(5)所定义的NURBS曲线,在参数μ处的曲率半径R(μ)计算如式(6)所示。
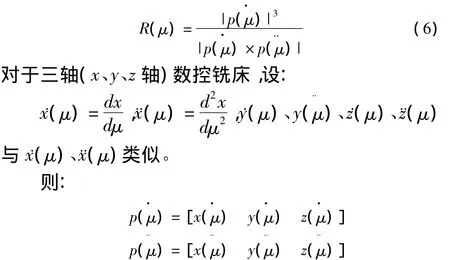
2.3 NURBS曲线插补轮廓误差控制
NURBS曲线插补轮廓误差自动控制的主要任务是根据曲线曲率半径大小提前获取满足轮廓误差条件下的机床进给速度信息,以控制插补器实时减速。
由式(1)、式(4)和式(5)可知,在给定的轮廓误差er情况下,根据曲率半径实时求解NURBS插补的约束进给速率vref比较困难,此时需要求解一个关于vref的一元三次方程,会严重影响数控系统插补的实时性。但是,由图2、图3可知,对于每一个给定的轮廓误差er和曲率半径R,对应着一个唯一的约束进给速率vref,因此对于一定的曲率半径R可以根据给定的er快速求得vref。
在NURBS曲线插补预插补阶段,建立图2、图3为一个关于曲线轮廓误差er与曲率半径之比er/R和约束进给速率vref与曲率半径之比vref/R的关系列表,根据该列表,采用线性插值方法则可比较方便的求出给定轮廓误差条件下的约束进给速率值vref。
实时插补分为以下几个步骤完成:
(1)计算当前插补点曲率半径R,根据允许的轮廓误差er得到er/R,确定其在关系列表中的区间范围,设er/R位于区间{[er/R]i,[er/R]i+1}内(i=1,2,…);
(2)在区间{[er/R]i,[er/R]i+1}采用线性插值求解er/R所对应的vref/R,从而得到当前的约束进给速率vref;
(3)对曲线不同曲率半径间进给速率的过渡处理以直线加减速方式进行,如果当前进给速度v与约束进给速率vref之间满足关系:|v-vref|<aT,则v=vref;否则采用式(7)进行速率修正,直到实际进给速率v=vref。

其中,a为机床允许加速度,T为插补周期。
需要指出的是,在算法第(3)步中,由曲率半径R得到当前插补点的允许进给速率vref后,为避免重复对本周期内的插补点进行校正计算,可将该vref作为下一个插补周期内的允许进给速率,以提高插补的实时性,本文在仿真实例中就采用了这种近似方法。
3 仿真实例
设被插补的三次NURBS曲线由下列参数定义:
控制顶点(单位:mm):(0,0,0),(15,-20,0),(30,-20,0),(60,20,0),(75,20,0),(90,0,0)
对应权因子:(1,6,10,10,6,1)
节点矢量:(0,0,0,0,0.5,0.5,1,1,1,1)
其它控制参数:ωn=120s-1,ξ=0.8,Kvx=Kvy=0.2ωn,插补周期T=4ms。机床许可加速度a=0.3m/s2,初始进给速率vb为600mm/min。
给定的NURBS曲线轮廓及曲率半径分布如图4所示。

图4 给定NURBS曲线轮廓及其曲率半径分布
3.1 采用轮廓误差自动控制算法的实际轮廓误差
给定轮廓误差er=0.001mm、0.005mm和0.01mm的情况下NURBS曲线插补实际进给速率如图5所示。

图5 不同轮廓误差下的实际进给速率
在给定轮廓误差er=0.001mm、er=0.005mm和er=0.01mm的情况下,NURBS曲线插补指令轨迹和实际轨迹在XY平面上的投影如图6所示(为表现轮廓误差,将轮廓误差进行了适当的放大),可以看出,给定的圆弧插补轮廓误差er越小,则实际加工轮廓越接近指令轮廓。在给定的er情况下,实际轮廓误差最大值分别仅为0.0006mm、0.0030mm和0.0058mm。

图6 采用轮廓误差自动控制算法的实际轨迹
可以看出,在相同的x坐标值下,实际进给速率与er值大小成正比,er值越大,则实际进给速率也越大。在曲率半径相对较小的位置处,则实际进给速率也相应变小。
3.2 不采用轮廓误差控制算法的实际轮廓误差
对于同一条NURBS插补曲线,选取图5中各曲线的近似中点速率(分别为800mm/min、1800mm/min和2500mm/min),不采用文中的轮廓误差算法进行恒进给速率仿真,则NURBS曲线插补指令轨迹和实际轨迹在XY平面上的投影如图7所示(左图对轮廓误差进行了适当的放大),可以看出,实际轮廓误差最大值分别达到了0.003mm,0.033mm和0.062mm,均大于采用廓误差自动控制算法的实际轮廓误差。
可见,本文所提轮廓误差控制算法能有效的减小NURBS插补中的实际轮廓误差。
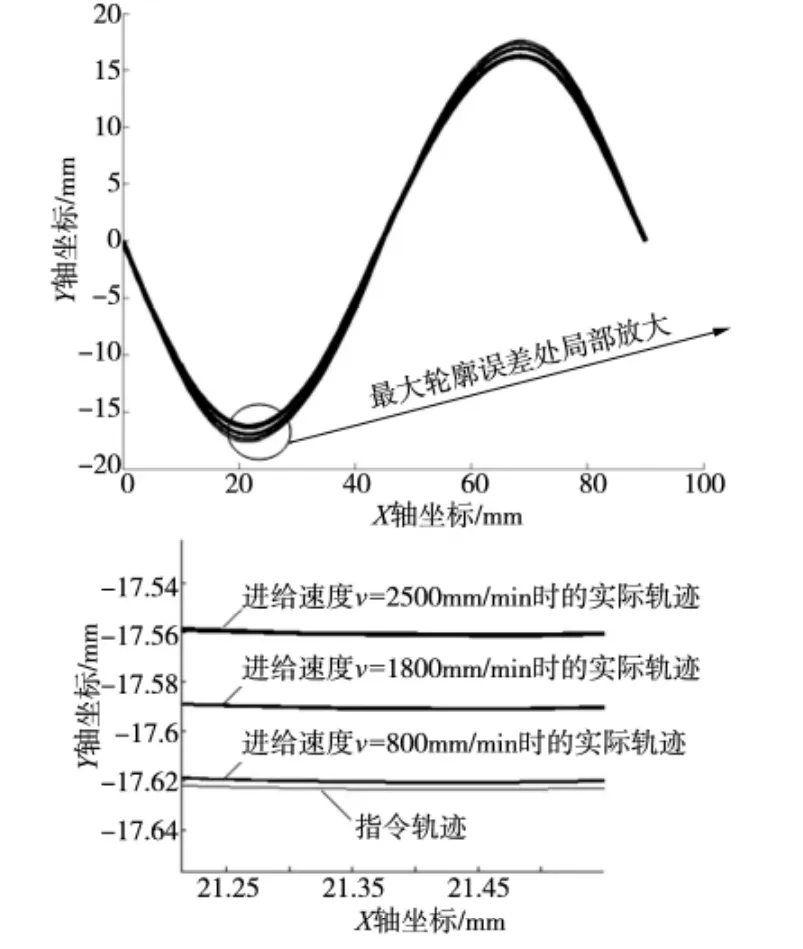
图7 不同进给速率条件一的实际轨迹
4 结论
针对高速高精度数控机床运动误差产生的原因,在分析圆弧插补理论轮廓误差的基础上,提出一种NURBS曲线插补轮廓误差控制算法,并进行算法仿真。仿真结果表明,该算法能有效的根据NURBS曲线的曲率半径实时获取适当的进给速率信息以控制实际轮廓误差。
[1]GE Fanuc Automation.Series 16i/18i/160i/180i/160is/180 is-MA for Machining Center Operator’s Manual[R].April 2000:79-83.
[2]赵国勇,赵福令,徐志祥.一种基于NURBS插补器的高精度交叉耦合控制方法[J].大连理工大学学报,2008,48(2):210-214.
[3]潘海鸿,杨微,陈琳,等.全程S曲线加减速控制的自适应分段NURBS曲线插补算法[J].中国机械工程,2010,21(2):190-195.
[4]北京发那科机电有限公司.数控系统的伺服装置(二)[J].机械工人(冷加工),2002(8):64-65.
[5]马方魁,郇极.数控机床NURBS曲线插补运动误差分析与仿真[J].中国机械工程,2008,19(20):2446-2449.
[6]李清新.伺服系统与机床电气控制[M].北京:清华大学出版社,1998.
[7]Huan Ji,Bahnregelung zur Bahnerzeugung an numerisch gesteuerten Werkzeugmaschinen[M].New York:Springer-Verlag Berlin Heidelberg,1982.
