一种工业无损检测超声图像降噪方法*

焦圣喜，魏宏建

(东北电力大学自动化工程学院，吉林 132012)

0 引言

近年来，基于成像的超声无损检测技术被广泛应用在核工业、机械工业、造船特种设备等工业领域。工业无损检测超声图像(简称工业超声图像)中的散斑噪声不仅降低了图像质量，而且严重影响了图像的人工判读和自动识别。均值滤波、中值滤波、Lee滤波、基于小波变换滤波、基于各向异性扩散方程滤波等是比较常用的散斑噪声降噪方法［1-2］，这些方法在一定程度上能够降低噪声，但也存在着保边性能不强、算法自适应差、算法复杂等不足。

粗集理论［3］是一种用于处理含糊和不确定性问题的数学工具，能够有效分析处理不完整、不一致、不确定等不完备信息，其已经被应用于图像降噪领域［4］。小波变换在时频域具有多分辨率的特性和表征信号局部信息的能力，能有效地从正常信号中提取瞬态成分，其同样已被应用于图像降噪［5-6］。针对常用的工业超声图像散斑噪声降噪方法又存在保边性能差等不足，以及在图像降噪过程中会出现不精确性和不完整性问题，本文提出一种新的基于粗集理论与小波变换的工业超声图像散斑噪声降噪方法。该方法利用粗集理论中的等价关系将工业超声图像划分为不同类型的子图，采用小波变换对含噪子图进行降噪处理。本文以实测的工业超声图像为实例给出了降噪处理过程及结果分析。

1 粗集理论简介

设论域U是一有限非空集合，R是U上的一个等价关系，则关系系统K=(U，R)为一个近似空间(又称知识库)，R可将论域U划分成互不相交的子集，即可形成U上的一个划分U/R。若有两个对象x∈U、y∈U且x≠y在U/R中的同一个子集，则称x与y是关于R不可分辨。设对象x∈U，X⊆U，［x］R表示R等价类(即在U/R中与x不可分辨的对象组成的集合)。当X可以用U/R中的某些子集的并表示时，称R可定义X，X为R精确集;否则X为R粗集。粗集理论中的“粗糙性”是通过边界域的存在来体现的，而边界域是由上、下近似刻画的。X关于R的下、上近似和边界域的定义如下：

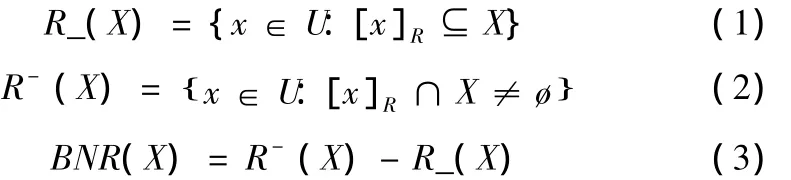
由上述定义可以看出：下近似R_(X)是对于知识(R，U)中肯定属于X的元素的集合;上近似R-(X)是对于知识(R，U)中可能属于X的元素的集合;边界域BNR(X)是对于知识(R，U)中不能确定属于X还是属于U-X的元素的集合。显然，BNR(X)≠Ø时，X为R粗集。

2 粗集与小波的工业超声图像降噪

基于粗集与小波的工业超声图像散斑噪声降噪主要包含两部分：①利用粗集理论中等价关系的概念对工业超声图像进行子图划分;②对含噪子图进行对数变换和小波分解，处理小波系数。

2.1 等价关系的工业超声图像的子图划分

将一幅由M×N个像素组成的待处理工业超声图像U看成一个知识系统，图像中的每个像素为U中的一个对象，R为能够表示图像散斑噪声特征的一等价关系族，则知识库K=(U，R)为图像U的一个近似空间。设处理图像U的滑动窗口大小为3×3，如图1所示。

图1 3×3滑动窗口

将该窗口分成4个方向模板：模板1由f(i-1，j-1)、f(i，j-1)、f(i-1，j)、f(i，j)组成;模板2 由f(i-1，j)、f(i，j+1)、f(i-1，j+1)、f(i，j)组成;模板3由f(i+1，j)、f(i，j+1)、f(i+1，j+1)、f(i，j)组成;模板4 由f(i+1，j)、f(i，j-1)、f(i+1，j-1)、f(i，j)组成。通过考察中心像素与周围模板像素灰度均值差的统计特征来定义滑动窗口中的等价关系［7］。

设f(i，j)为窗口中心像素的灰度值，第k(k=1，2，3，4)个模板除中心像素外的其它像素灰度值和为fk，则中心像素与第k个模板的灰度差异为d(k)，其表达式如下：

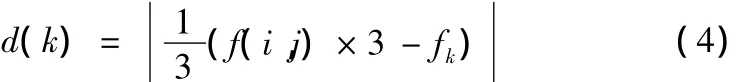
则窗口中心像素与周围模板灰度差异均值mean(i，j)为：

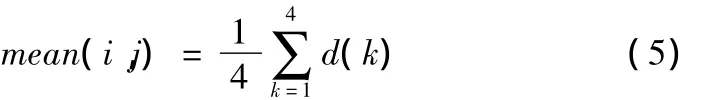
窗口中心像素与周围模板灰度差异方差var(i，j)为：

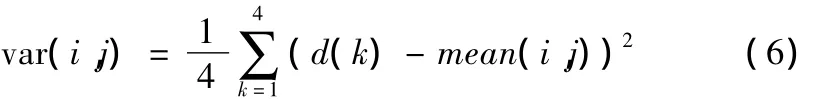
定义如下两个等价关系：

(1)等价关系Rc1像素与其周围模板灰度差异均值大于阈值thr_mean，即Rc1(x)={x：mean(i.，j)＞thr_mean}，则Rc1表示与周围模板灰度差异均值较大的像素。

(2)等价关系Rc2像素与其周围模板灰度差异方差小于等于阈值thr_var，即Rc2(x)={x：var(i.，j)≤thr_var}，则Rc2表示与周围模板灰度差异方差较小的像素。

显然，含噪像素与周围模板灰度均值差异较大且与周围模板灰度差异方差较小，用X表示含噪像素集合，则X的下、上近似和边界域如下：

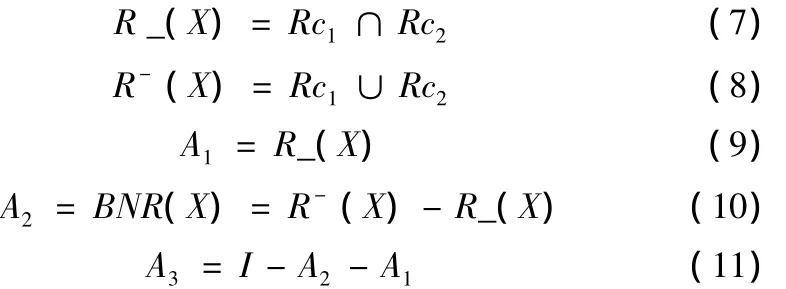
式(7)～(11)中：R_(X)表示所有确定含噪像素的集合;R-(X)表示所有可能含噪像素的集合;A1、A2、A3分别为确定含噪子图、可能含噪也可能不含噪子图及确定不含噪子图，A1、A2即为需要降噪的子图。

2.2 小波变换中小波系数的处理

利用粗集理论中的等价关系将工业超声图像U划分为3个子图，对需要降噪的子图A1、A2首先完成对数变换然后进行小波分解。在将A1与A2小波分解后，利用具有自适应特点的阈值函数对小波系数进行处理［8］，阈值函数如下：

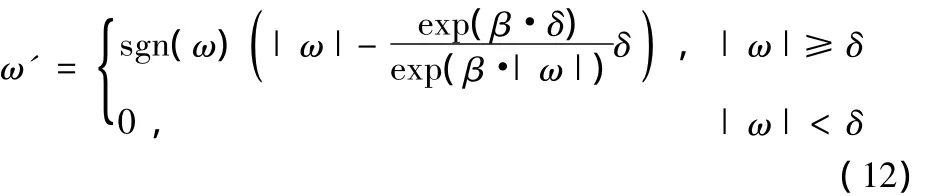
式中：ω为小波系数;ω'为处理后的小波系数;β为非负数，在实际应用中应该取一个适中的值;δ为阈值。采用式(13)［9］确定 δ：

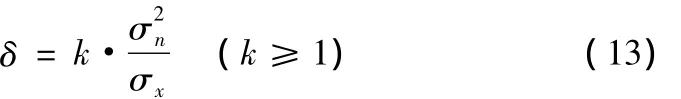
其中：k值与图像质量有关，本文取k=log2(L)(L为子带长度);为噪声方差，这里采用HH1子带的方差作为噪声方差的估计值(HH1表示小波分解的第一层对角高频子带);σx为子带系数标准差，其可由下式进行估计：

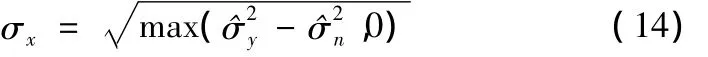
上式中为观测子带的方差，依据式(15)计算：

式(15)中Mj为第j个子带中系数个数;y(k)为第j个子带中的小波系数。

3 实验结果与分析

3.1 降噪算法评价指标

图像质量除了从主观视觉上判断外还可以采用一些客观指标来评价，本文选用峰值信噪比和边缘保持度两个指标来衡量降噪算法的效果［10］。

(1)峰值信噪比(PSNR)

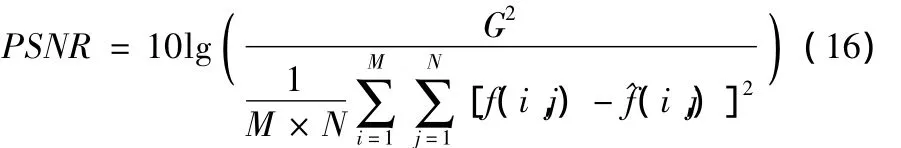
其中：G为图像像素最大值;f(i，j)为原图像各像素值;^f(i，j)为降噪后图像各像素值。PSNR值越大，图像质量越好。

(2)边缘保持度(α)

其中：Δf、是用3×3的Laplacian算子对f高通滤波的结果;¯、代表Δf、的均值。α是用来衡量降噪算法对图像边缘的保持程度，α值应接近于1。

3.2 实验主要步骤

(1)根据式(4)计算每个滑动窗口的中心像素与4个方向模板的灰度差异。

(2)根据式(5)和(6)计算每个滑动窗口的中心像素与周围模板灰度差异均值与方差。

(3)确定阈值thr_mean和阈值thr_var，进而确定R_(X)和R-(X)，从而划分最终的子图A1、A2和A3。

(4)对子图A1与A2：

①取对数变换并进行小波分解。

②估计噪声方差

③保留低频小波系数，对各高频子带做如下处理：

(i)由式(14)和式(15)估计每个子带的子带系数标准差σx。

(ii)由式(13)计算各子带的自适应阈值。

(iii)用式(12)处理每个子带的小波系数。

④对未处理的低频小波系数和处理后得到的高频小波系数进行小波逆变换。

⑤做指数变换，得到降噪后的子图。

(5)A3与降噪后的A1、A2叠加，获得最终的降噪工业超声图像。

(6)由式(16)和式(17)计算工业超声图像降噪后的边缘保持度和等效视数。

3.3 本文算法与其它降噪算法比较分析

某工业金属铸件无损检测的截面超声图像如图2a所示，为了验证本文算法的有效性，对图2a中的散斑噪声分别利用中值滤波、均值滤波、小波软阈值滤波和本文算法进行降噪处理，处理后的图像如图2b～e所示。其中：小波软阈值处理时，采用sym4小波，分解层数为3。本文算法处理时，阈值thr_mean与thr_var分别为图像差异均值和差异方差最大值的0.5倍，采用sym4小波，分解层数为3;式(12)中β取值为6。

从图2可以看出：中值滤波及均值滤波能够很好地滤除散斑噪声，但是目标的边缘严重模糊;小波软阈值主观视觉得到了较大改善，边缘保持较好但降噪效果稍差;本文算法在保证了较好地保边性能的同时保留了部分有效细节信息，降噪效果比前三种好，从而说明本文算法是有效可行的。

图2 工业超声图像降噪效果比较

表1为算法效果评价指标值。表中的结果也显示本文提出的算法在峰值信噪比和边缘保持度两个方面均优于其它三种算法。

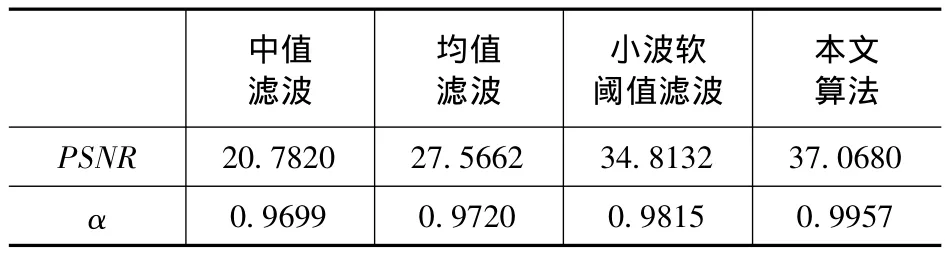
表1 图像降噪后算法效果评价指标

4 结论

工业无损检测超声图像散斑噪声降噪问题是工业超声图像处理领域的一个重要问题。本文结合粗集理论和小波变换理论，研究了一种工业超声图像降噪方法。实验结果表明：该方法不仅具有良好的降噪效果和边缘保持性能，而且与中值滤波、均值滤波及小波软阈值滤波相比有良好的主观视觉效果，算法是有效可行的。虽然本文提出的方法有良好的降噪效果和保边性，但是仍然存在少量小细节丢失现象，需要进一步改进和研究。

［1］H.W.Yang，X.L.Li，J.P.Wu，et al.Complex method forspeckle noise reduction in the sonar image from a small underwater target［C］.2011 2nd International Conference on Artificial Intelligence，Management Science and Electronic Commerce，Dengfeng，China，2011：254 －256.

［2］N.Modalavalasa，K.S.Prasad，S.S.Rani，et al.A quantitive evaluation of various spatial filters for underwater sonar images denoising application［J］.Annals of the Faculty of Engineering Hunedoara，2012，X(1)：47 －51.

［3］Z.Pawlak.Rough sets［J］.International Journal of Computer and Information Sciences，1982，11(5)：341 －356.

［4］G.Xie，C.D.Yan，T.R.Cao，et al.ROI of HRCT enhancement and de-noising based on rough set［C］.2010 International Conference on Computational Aspects of Social Networks.Taiyuan，China，2010：196 －199.

［5］M. Amirmazlaghani，H. Amindavar.Wavelet domain bayesian processor for speckle removal in medical ultrasound images［J］.IET Image Processing，2012，6(5)：580 －588.

［6］I.Firoiu，C.Nafornita，D.Isar，et al.Bayesian hyperanalytic denoising of SONAR images［J］.IEEE Geoscience and Remote Sensing Letters，2011，8(6)：1065 －1069.

［7］邢占峰，吕扬生，张力新，等.粗集理论在超声心动图噪声抑制中的应用［J］.医疗设备信息，2003，18(4)：4－7.

［8］杨恢先，王绪四，谢鹏鹤，等.改进阈值与尺度间相关的小波红外图像去噪［J］.自动化学报，2011，37(10)：1167－1174.

［9］万晟聪，杨新.基于自适应小波阈值的SAR图像降噪［J］.信号处理，2009，25(6)：874－881.

［10］郭海涛，刘星洁，石建宏.贝叶斯改进阈值超声图像去噪方法［J］.应用声学，2012，31(6)：468－473.