线性回归模型的置信区间与预测区间应用分析*
2013-09-11张林泉
张林泉
(广东女子职业技术学院,广东广州 511450)
线性回归模型的置信区间与预测区间应用分析*
张林泉
(广东女子职业技术学院,广东广州 511450)
论述线性回归的因变量置信区间和因变量个别值的预测区间原理后,结合实例分析了学生总数与季度营业额2个变量的关系.研究发现,学生总数与季度营业额关系存在很强的正向线性关系(r=0.950 1),可决系数(R2=0.902 7)可以解释总平方和中的90.27%,表明其拟合度很好.之后,给出了因变量平均值的置信区间、因变量个别值的预测区间及图形.
回归分析;置信区间;预测区间;学生总数;季度营业额
一元线性回归预测法是指成对的2个变量数据分布大体上呈直线趋势时,运用合适的参数估计方法,求出一元线性回归模型,然后根据自变量与因变量之间的关系,预测因变量的趋势[1].进行一元线性回归预测时,必须选用合适的统计方法估计模型参数,并对模型及其参数进行统计检验.对于自变量x的一个给定值xp,根据回归方程得到因变量y的一个估计区间.区间估计有2种类型:置信区间估计(confidence interval estimate)和预测区间估计(prediction interval estimate).利用回归方程进行预测时,会出现因变量置信区间和因变量个别值的预测区间的误用问题.笔者试图对二者关系进行分析,同时阐明影响区间宽度的因素.
1 对因变量均值的区间预测
利用估计的回归方程,对于自变量x的一个给定值xp,求出因变量y的平均值的估计区间,这一估计区间称为置信区间(confidence interval).因变量均值时的方差的估计值为

E(yp)在1-α置信水平下的置信区间为[2-3]


2 对因变量个别值的区间预测
利用估计的回归方程,对自变量的一个给定值x0,求出因变量y的个别值的估计区间,这一区间称为预测区间(prediction interval).因变量个别值的方差的估计值为
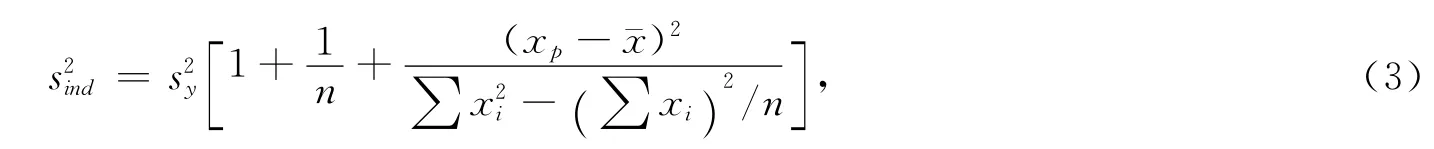
因变量个别值的预测区间为[3-4]

3 应用实例
数据(见表1)源于临近大学校园的10家餐馆的样本,xi是学生总数(单位:千人),yi是季度营业额(单位:千美元).
3.1 确定估计回归方程
n=10,经计算可得
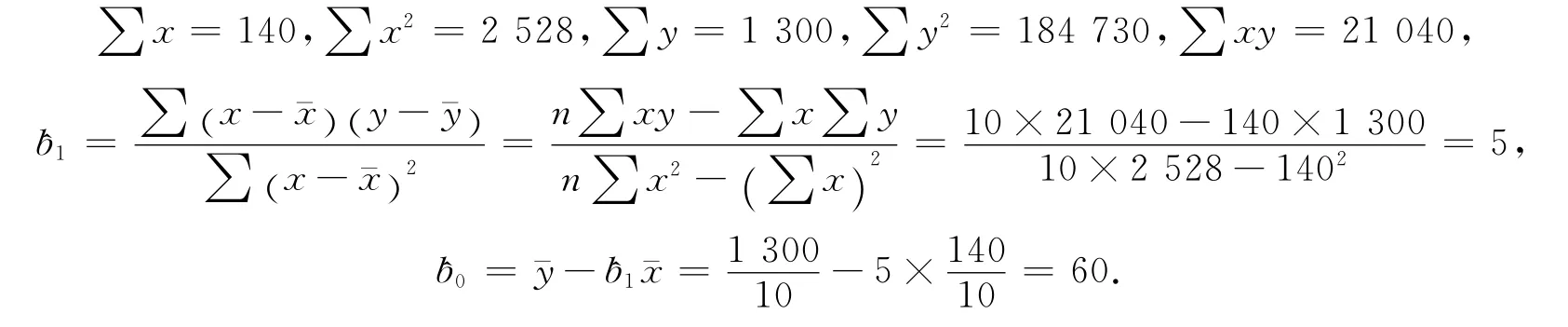
因此,建立的一元线性估计回归方程为^y=60+5x.
3.2 判断拟合优度情况
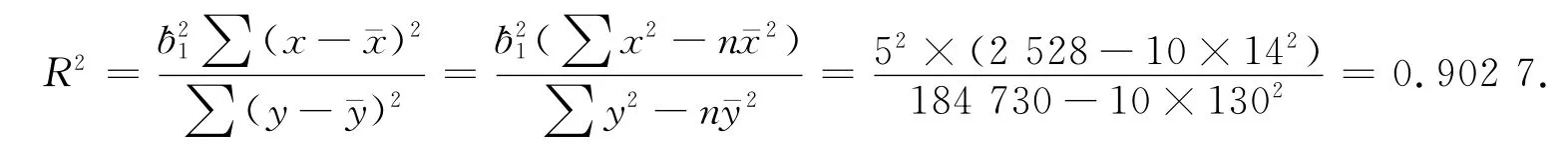
若用估计回归方程^y=60+5x来预测营业额,则可以解释总平方和中的90.27%,说明回归方程拟合度很好.样本相关系数=(β1的符号)表明x和y之间具有很强的正向线性关系.
3.3 显著性检验
3.3.1 回归方程的显著性检验(线性关系的检验) 提出假设H0,即学生总体与营业额之间的线性关系不显著.计算检验统计量F(见图1),

因为74.248 37>F0.01(1,8)=11.258 6,可知显著水平为0.01时,β1不等于0,所以拒绝原假设,认为所建立的线性回归模型是显著的.学生总体与营业额之间线性关系显著,即回归方程线性关系显著.
3.3.2 回归系数的显著性检验 提出假设H0:β1=0(没有线性关系),H1:β1≠0(有线性关系).计算检验的统计量t(见图2),
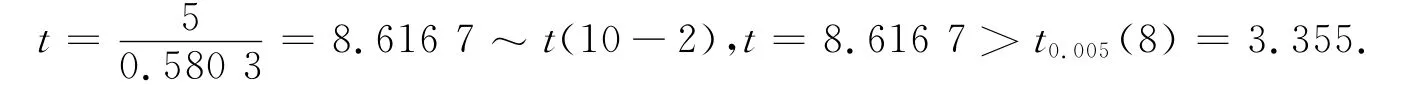
对应于显著水平为0.01时,自由度为n-2=10-2=8,双尾检验t值是t0.005(8)=3.355.因8.616 7>3.355,在显著水平为0.01下,β1不等于0,故学生总体与营业额之间存在显著关系,表明自变量是影响因变量的一个显著因素.
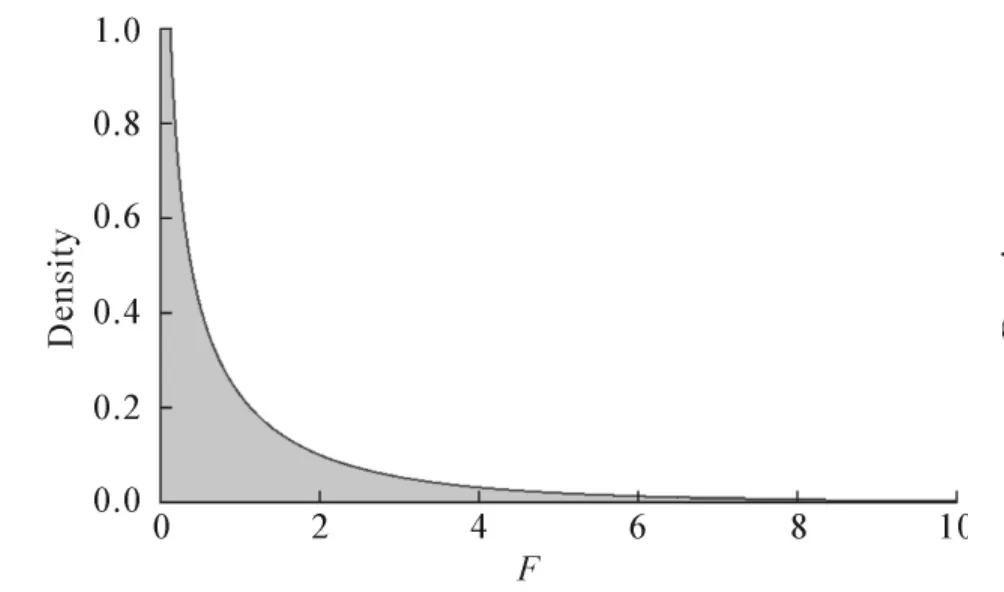
图1 F分布,df1=1,df2=8的概率密度函数

图2 T分布,df=8的概率密度函数
3.4 利用回归方程进行预测
3.4.1 因变量平均值的置信区间 若x=xp=10,点估计^yp=60+5×10=110,则
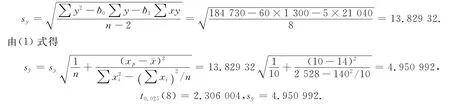
由(2)式得

即置信度为95%的因变量均值的置信区间为(98.582 991 48,121.417 008 5),学生数为10千名的学校,其营业额的平均值有95%的可能位于98.583 0和121.417 0之间.
3.4.2 因变量个别值的预测区间 若x=xp=10,有^yp=60+5×10=110,则由(3)式可得

即位于有10千名学生的校园附近的单个餐馆营业额95%的预测区为(76.127 45,143.872 5).
图3显示显著水平为0.05时,自由度为8的双尾检验t概述密度函数.由图4可知,因变量个别值的预测区间总是要比因变量平均值的置信区间宽,这是因为在对单个响应与响应均值的预测中包括了更多的不确定性.因变量平均值的预测值与真实平均值有误差,主要是受抽样波动影响;因变量个别值的预测值与真实个别值的差异,不仅受抽样波动影响,而且受随机扰动项的影响[5].
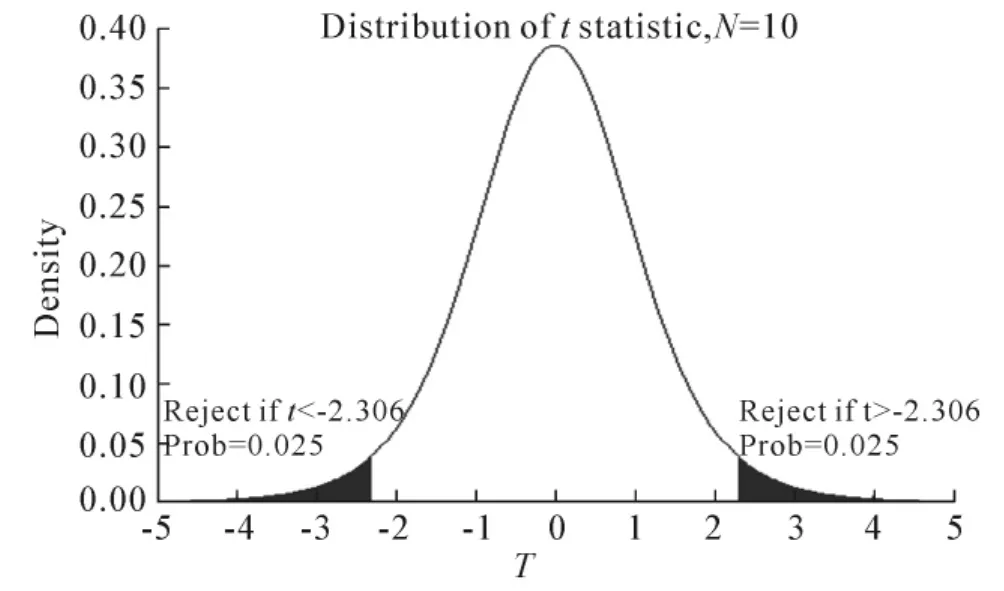
图3 T分布,df=8的概率密度函数

图4 均值置信区间带和个别值的预测区间带
4 结语
讨论了如何利用样本数据建立回归分析模型,并进行相应的显著性检验,由估计回归方程给出因变量均值的置信区间和因变量个别值的预测区间;应用SPSS和MATLAB做出因变量均值的置信区间和因变量单个值的预测区间等相关图形.综上分析,影响区间宽度的因素有用于预测的xp与x-的差异程度、置信水平、数据的离散程度、样本容量.区间宽度随xp与x-的差异程度的增大而增大,xp与x-的差异程度越大预测精度越差;区间宽度随置信水平的增大而增大;区间宽度随离散程度的增大而增大;区间宽度随样本容量的增大而减小.
[1] 徐国祥.统计学[M].上海:上海财经大学出版社,2007.
[2] 庞 皓.计量经济学[M].北京:科学出版社,2007:48-54.
[3] [美]戴维·R·安德森.商务与经济统计精要(英文版)[M].第2版.北京:机械工业出版社,2005:364-422.
[4] RON LARSON,BESTY FARBER.基础统计学(英文版)[M].第4版.北京:中国人民大学出版社,2010:330.
[5] [美]黙里.计量经济学:现代方法:上(经济学精选教材·英文影印版)[M].北京:北京大学出版社,2009:175.
(责任编辑 向阳洁)
Application of Confidence Intervals and Prediction Intervals of Linear Regression
ZHANG Lin-quan
(Guangdong Women’s Polytechnic College,Guangzhou 511450,China)
After describing the principle of confidence intervals and prediction intervals,this paper,which applies it to analyze the relationship between such two variables as student size and quarterly turnover,tests regression equation.And the result shows that there exists high degree of fitting between these two variables since there exists a positive linear relationship between the two variables(r=0.950 1)and a bout 90.27%of the variation in the quarterly turnover data is explained by student size;The paper offers not only confidence intervals for the mean of y and prediction intervals for an individual y by using estimated equation,but some relevant graphs as well.
regression analysis;confidence intervals;prediction intervals;student size;quarterly turnover
F222.1;O212.7
A
10.3969/j.issn.1007-2985.2013.06.005
1007-2985(2013)06-0015-04
2013-04-15
广东省教育科学“十二五”规划2012年度项目(2012JK078)
张林泉(1965-),男,广东化州人,广东女子职业技术学院副研究员,硕士,主要从事统计、数量经济学与数学教学研究.
