丢番图方程5·2x＋7·3y＝11＋2z·3w的计算机辅助解法＊

邓谋杰，周小娥

（海南大学信息科学技术学院，海南海口 570228）

丢番图方程5·2x＋7·3y＝11＋2z·3w的计算机辅助解法＊

邓谋杰，周小娥

（海南大学信息科学技术学院，海南海口 570228）

利用计算机辅助方法，给出了指数丢番图方程5·2x＋7·3y＝11＋2z·3w的全部整数解.

指数丢番图方程；整数解；计算机辅助解法

1 问题的提出

指数丢番图方程在丢番图方程理论中占有重要的地位，其研究成果不仅在数论研究中有重要的理论意义，同时还有重要的应用价值.例如，用于高精度对数计算、有限单群的分类等［1］.但对指数丢番图方程的研究常常是比较困难的，对于三元以上的指数丢番图方程，其研究尤为困难.Christopher M.Skinner［2］用Baker方法证明了如下结论：

定理1 指数丢番图方程

除去0解x＝y＝z＝w＝0外，仅有6组非0整数解

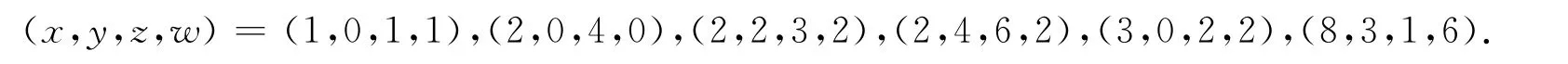
Baker方法是求解丢番图方程的一个重要的高等方法，但常常需要很大的计算量.文献［2］为求解方程（1），将对数计算到小数点后220位.在文献［2］结尾，作者指出求解形如（1）式的指数丢番图方程需要使用诸如对数的线性形式之类的高等方法.笔者将借助计算机以上定理1的一个较为简单的初等证明.

2 相关引理

引理1 若（x，y，z，w）是（1）式的非0整数解，则它必满足下列同余式之一：

证明 由文献［3］知，

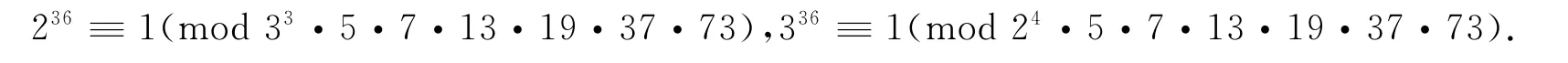
利用模m＝4，8，16，32，3，9，27，81，5，7，13，19，37，73，考虑同余式5·2x＋7·3y≡11＋2z3w（mod m），可得上述结论，但计算十分冗长.若使用计算机，只要在1≤x≤36，0≤y≤35，1≤z≤36，0≤w≤35的范围内检验.设m＝min｛x，z，4｝，n＝min｛y，w，3｝，在PC机上用UBASIC语言编写的简短程序对模2m· 3n·5·7·13·19·37·73进行检验，运行时间仅10s.

3 定理的证明

下面给出定理1的证明，分2种情形讨论.

（Ⅰ）x＝0的情形.

此时（1）式右端必为奇数，于是有z＝0.原方程化为7·3y－3w＝6.

若w＝0，显然有y＝0；若w＞0，则y＞0，但此时显然7·3y－3w＞6，故不可能.于是x＝0时必有y＝z＝w＝0.

（Ⅱ）x＞0的情形.

设（x，y，z，w）为（1）式的任一非0整数解，由引理1知，仅有下列6种情形.

（ⅰ）（x，y，z，w）＝（1＋36k，36l，1＋36s，1＋36t）.故有

由236≡1（mod 9），对（2）式取模3可得l＝0；此时（2）式左端模9余8，由此可知必有t＝0，于是有5· 236k＋1－3·236s＋1＝4，从而有k＝s＝0.因此，在情形（ⅰ），（1）式仅有1组解（x，y，z，w）＝（1，0，1，1）.

对（3）式取模8可得k＝0，再取模16可得s＝0，于是原方程化为23·336t－7·336l＝1，由此显然推出l＝t＝0.因此，在情形（ⅲ），（1）式仅有1组解（x，y，z，w）＝（2，2，3，2）.

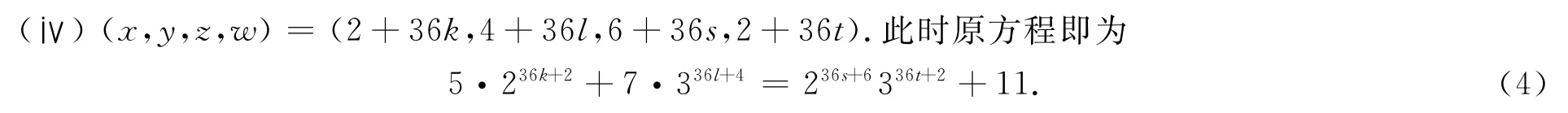
对（4）式取模8可得k＝0，再取模27得t＝0，于是原方程化为236s＋6－7·336l＋2＝1.由236≡1（mod 27），取模27可得l＝0，从而s＝0.因此，在情形（ⅳ），（1）式仅有1组解（x，y，z，w）＝（2，4，6，2）.

（ⅴ）（x，y，z，w）＝（3＋36k，36l，2＋36s，2＋36t）.仿照情形（ⅳ）的讨论可知，在情形（ⅴ），（1）式仅有1组解（x，y，z，w）＝（3，0，2，2）.

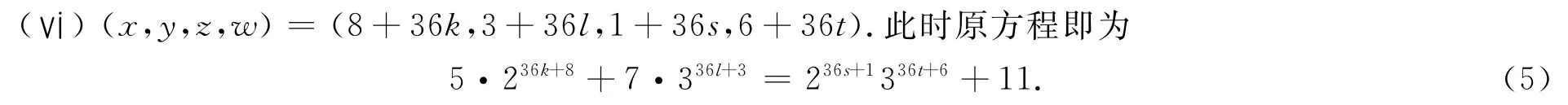
由于336≡1（mod 16），若s＞0，对（5）式取模16可得－1≡11（mod 16）的矛盾结果，因此s＝0，z＝1.由于［3］

对（5）式取模81，97，256可得如下4种情形（在PC机上利用UBASIC编写的简短程序进行检验）：

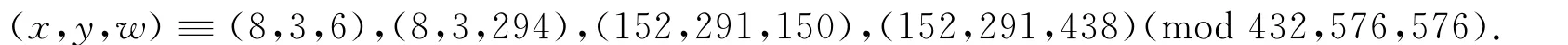
（a）在y≡3（mod 1 152），x＞8时，由于31152≡1（mod 512），对（5）式取模512可得189≡2·36＋11≡445（mod 512）的矛盾.于是x＝8，进而得到y＝3，w＝6.

在y≡579（mod 1 152），由于3192≡－1（mod 280 321），当w≡6（mod 1 152）时，对（5）式取模2 80 321得

但这将导致

的矛盾.当w≡6＋576（mod 1 152）时，由于348≡－1（mod 76 801），对（5）式取模76 801得

（d）与情形c类似，取模64 513可导致矛盾.

由以上讨论知，此时（1）式仅有1组解（x，y，z，w）＝（8，3，1，6）.

综合情形（Ⅰ），（Ⅱ），定理1得证.

［1］ 曹珍富.丢番图方程引论［M］.哈尔滨：哈尔滨工业大学出版社，1989.

［2］ CHRISTOPHER M SKINNER.On the Diophantine Equation apx＋bqy＝c＋dpzqw［J］.Journal of Number Theory，1990，35：194－207.

［3］ BRILLHART J，LEHMER D，SELFRIDGE J，et al.Factorizations of bn－1，b＝2；3；5；6；7；10；11；12up to High Powers［M］.2nd Edition.Providence：Amer.Math.Soc.，1988.

（责任编辑 向阳洁）

Computer Aided Solution of the Diophantine Equation 5·2x＋7·3y＝11＋2z·3w

DENG Mou-jie，ZHOU Xiao-e
（College of Information Science and Technology，Hainan University，Haikou 570228，China）

With computer assistance，all the solutions in integer of the Diophantine equation 5·2x＋7·3y＝11＋2z·3ware given in this paper.

exponential diophantine equation；solutions in integer；computer aided solution

O156.7

A

10.3969／j.issn.1007－2985.2013.06.001

1007－2985（2013）06－0001－03

2013－04－16

海南省自然科学基金资助项目（113002）

邓谋杰（1960－），男，黑龙江汤原人，海南大学信息科学技术学院教授，硕士，主要从事丢番图方程研究.