一个较为精确的半离散Mulholland’s不等式加强＊

聂彩云

（吉首大学数学与统计学院，湖南吉首 416000）

一个较为精确的半离散Mulholland’s不等式加强＊

聂彩云

（吉首大学数学与统计学院，湖南吉首 416000）

利用Jensen-Hadmamard’s不等式及加强的Hölder不等式，对半离散的Mulholland’s不等式作了改进，建立了一些新的不等式.

Mulholland’s不等式；权系数；算子表述；Hölder不等式

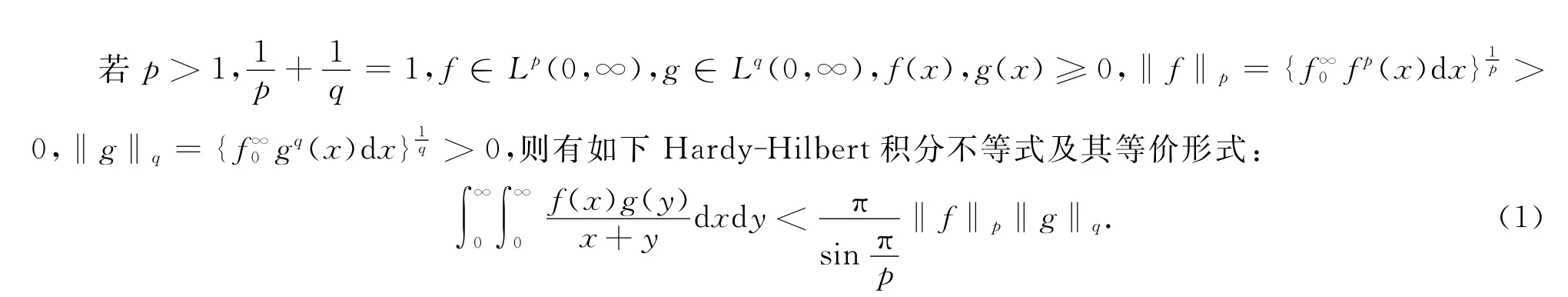
（1）式称为Hardy-Hilbert积分不等式，它在分析学中有重要的应用.

文献［1］建立了如下一个新的较精确的半离散Mulholland不等式：

笔者利用改进的Hölder不等式对（2）式进行加强，从而建立一些新的不等式.

1 相关引理及其证明

为了方便起见，先介绍一些符号：

证明见文献［2－3］.

引理2 若λ1＞0，0＜λ2≤1，λ1＋λ2＝λ，α≥，定义权函数

2 主要结果

即（3）式成立.

下面讨论Ra的表达式.选取由（4）式所定义的权函数（x，n），有由引理1，有

注1 （3）式即为（2）式的改进式.

［1］ YANG Bi－cheng.On a More Accurate Half－Discrete Mulholland’s Inequality and Extension［J］.Journal of Inequalities and Aplications，2012，Doi：10.1186／1029－242X－2012－70.

［2］ HE Le－ping，GAO Ming－zhe，JIA Wei－jian.On a New Strengthened Hardy－Hilbert’s Inequality［J］.Journal of Mathematical Research and Exposition，2006，26（2）：276－282.

［3］ HE Le－ping，JIA Wei－jian，GAO Ming－zhe.A Hardy－Hilbert’s Type Inequality with Gamma Function and Its Applications［J］.Integral Transforms and Special Functions，2006，17（5）：355－363.

［4］ HE Le－ping，GAO Ming－zhe.A Hilbert Integral Inequality with Hurwitz Zeta Function［J］.Journal of Mathematical Inequalities，2013，7（3）：377－387.

（责任编辑 向阳洁）

A More Accurate Strengthend Half－Discrete Mulholland’s Inequality

NIE Cai－yun
（College of Mathematics and Statistics，Jishou University，Jishou 416000，Hunan China）

By means of Jensen-Hadmamard’s inequality and a sharpened Hölder’s inequality，the half－discrete Mulholland’s is improved，and some new inequalities are established.

Mulholland’s inequality；weight coefficient；operator expression；Hölder inequality

O178

A

10.3969／j.issn.1007－2985.2013.06.003

1007－2985（2013）06－0009－03

2013－06－19

聂彩云（1963－），女，湖南永顺人，吉首大学数学与统计学院副教授，主要从事函数论及应用研究.