定量检测体外诊断试剂的线性评价方法介绍及其在肿瘤标志物试剂盒检验中的应用

石大 伟，沈 舒， 王 菲 菲， 张 春 涛＊ （中 国 食 品 药 品 检 定 研 究 院，北京 00050； 卫生部生物技术产品检定方法及其标准化重点实验室）

线性是定量体外诊断试剂 （Quantitativein vitroDiagnostic Products，qIVD）质量的主要指标之一，对数据的线性评价是qIVD产品注册检验的重要内容［1－3］。目前，我国qIVD产品注册检验主要包括对产品线性、准确性、特异度、最低检出限和精密度等项目的考核［1］，而线性是qIVD产品准确性评价的基础，也是整个qIVD产品质量评价的关键。ISO 18113-1：2009 “InvitroDiagnostic Medical Devices-Information Supplied by the Manufacturer（Labelling）”建议参考美国临床实验室标准化协会（Clinical and Laboratory Standards Institute，CLSI）指南EP6-A “Evaluation of the Linearity of Quantitative Measurement Procedures：A Statistical Approach”（指南EP6-A）对qIVD产品线性进行评价和验证［2］。指南EP6-A也是美国FDA认可的CLSI文件之一［3］，在 《体外诊断试剂分析性能评估系列指导原则 （征求意见稿）》中，我国食品药品监督管理总局 （CFDA）也参考了该指南，对企业产品进行线性范围评估及准备线性范围评估资料提供原则性指导［1］。该指南所述方法的应用范围广，可以指导生产厂商初次建立和验证qIVD产品的线性，也可用于使用者 （如：临床检验人员）评估已建立的线性关系。在qIVD产品注册检验工作中，用于数据拟合的回归方程是企业在研发中已确定并在申报资料中提供的。相应地，质量检验机构的主要工作是对企业标准的内容进行复核，即按提供的回归方程对试验数据进行拟合分析，验证其正确性，而并不需要对多种方程进行比较来建立产品的线性范围。因此，参考指南EP6-A并兼顾了注册检验工作的特点，本文提出了qIVD产品注册检验中线性评价的建议方法，希望能有助于进一步科学地规范相关检验工作。

1 qIVD产品注册检验线性评价的建议方法介绍

qIVD产品注册检验线性评价的建议方法分为2个部分：对产品 （试剂盒）校准品的线性评价和利用样本对试剂盒线性的评价。对于封闭的、自动化系统上使用的试剂盒，试剂盒校准品的线性评价通常是系统直接给出的，但若可能，也应获得初始的检测数据对试剂盒校准品的线性进行评价。具体步骤如下。

1.1 试剂盒校准品的线性

（1）试剂盒校准品的要求：试剂盒校准品的浓度应覆盖整个厂家声明的线性范围的系列浓度，某些类别试剂盒的校准品数量应不少于4个［4］。

（2）绘制散点图及离群值的发现和处理：散点图的绘制对于线性评价非常重要，其作用包括：①初步获得数据的线性关系 （直线、抛物线或S型曲线等），以初步核实企业标准中声明的线性回归方程的正确性。比如：若声明使用直线方程拟合，则原始数据点很可能分布在一个不太宽的具有线性趋势的条形区间里。若声明使用双对数、loglogit、四参数方程对数据进行拟合，则原始数据点应呈现具有拐点的曲线分布。此外，对于声明进行直线方程拟合的数据，还可对拟合直线是否应过原点，即回归方程是否含有截距项作出初步判断；②观察数据的精密性，当与其他浓度相比某个浓度水平精密度较低时，特别是发生在声明的线性范围的两端，应注意线性范围是否过宽的情况；③发现离群值。明显的离群值可以通过观察散点图被容易地发现。若只有一个离群值，则可删除而不必用重复实验，但当离群值多于一个时，应仔细分析，找出问题所在并重复实验，然后使用新的数据进行分析。

（3）数据转换：如果企业标准中声明，应按要求对数据进行相应的转换。在实际工作中，以非竞争性标记免疫分析为原理的蛋白检测qIVD产品一般使用双对数log-log转换 （自然对数或常用对数，二者仅回归方程的截距不同）；以竞争性标记免疫分析为原理的蛋白检测qIVD产品一般使用log-logit转换，即检测值做logit转换，logitY＝log［B/B0/（1－B/B0）］，B：某浓度下的样品测定值，B0：最低浓度下的样品测定值，而样本浓度值做对数变换（自然对数或常用对数）；以荧光PCR为原理的核酸检测qIVD产品一般需将浓度值做对数转换。

（4）线性回归分析：使用企业声明的方程，通过 适 当 的 软 件， 如：Analyse-it、SAS、SPSS、Microsoft Excel，对数据进行回归分析，置信水平一般为双侧0.05 （α＝0.05），计算方程的相关系数r或确定系数R2，应符合企业注册标准中的规定。根据行业标准，相关系数r的绝对值一般应不小于0.98。当散点图明显提示拟合的曲线可能过原点时，如图1，或企业注册标准给出的线性范围包含零点时，或数据计算是已扣除零点样本读数时，应注意检验回归方程中的截距项。在SAS中，可以通过在proc reg的model中加 “/noint”选项来拟合不含截距项的回归方程，在Analyse-it软件中可以在拟合分析时勾选相应选项来实现。

1.2 利用样本对试剂盒线性的评价

（1）样本要求：qIVD产品注册检验线性评价涉及的样本通常是临床样品、企业内部校准品、国家参考品或国际标准品等。它们应为不少于5个、能覆盖整个厂家声明的线性范围的系列浓度的样本，每个浓度水平的样本测定不少于2次。各样本可以用绝对浓度或相对值来标识。指南EP6-A建议，理想的情况下，应使用高值和低值临床样本按比例混合得到系列浓度的样本，这主要是考虑基质效应对检测结果的影响。在注册检验中，对于不同的待测物，样本可以是按上述要求预先制备好的系列浓度的冰冻或冻干样本，也可在实验前使用特定稀释液或蒸馏水稀释高值样本配制成系列浓度样本。

（2）绘制散点图及离群值的发现和处理：与“1.1”中对试剂盒校准品的要求相同。

（3）线性回归分析：通过适当的软件对数据分别拟合一次多项式 （y＝b0＋b1x）、二次多项式（y＝b0＋b1x＋b2x2）和 三 次 多 项 式 （y＝b0＋b1x＋b2x2＋b3x3）回归方程，计算回归系数的统计学显著性 （t检验）和回归标准误，置信水平一般为双侧0.05 （α＝0.05）。一次多项式回归方程即为直线回归方程。当多个方程的回归系数均有统计显著性时，应将回归标准误最小的方程判定为最优方程。①若企业声称数据应符合线性 （直线回归方程），且二次方程的回归系数b2，或三次方程的回归系数b2或b3无统计学显著性，则试剂盒线性符合相应评价标准的要求；若二次方程的回归系数b2，或三次方程的回归系数b2或b3有统计学显著性，则需要比较各样品下最优方程与直线回归方程待测物浓度预测值的差值。若各样品下浓度预测值的差值均小于事先设定的允许误差，则仍可认为数据符合直线回归方程，判为线性；若存在个别浓度水平的差值大于事先设定的允许误差，且浓度水平分布于线性范围的两端，则需剔除这些浓度点，缩小线性范围，再次拟合回归方程，重新进行评价。重新评价后，若数据仍不符合直线方程，则该试剂盒数据不符合评价标准的相应要求 （非线性）。②若企业声称数据应符合非直线回归方程，且数据拟合显示二次方程的回归系数b2，或三次方程的回归系数b2或b3有统计学显著性，则可认为试剂盒线性符合相应评价标准的要求，否则可认为不符合标准的相应要求。③由于在不同的线性范围区间，测量误差可为一个非恒定的值按比例变动，这时允许误差用百分比表示，上述某浓度水平下，最优方程与直线回归方程浓度预测值的差值需除以该水平的实际测量值的均值。允许误差应符合企业注册标准的相应要求，一般为5%或不超过该项目临床允许总误差的1/4。

（4）精密度分析：按下面公式计算精密度：其中ri为样本i水平的浓度平均值，rij为样本的浓度值，L为样本数，R为重复检测的次数。精密度可用绝对偏差或相对偏差来表示。当为相对偏差时，SDr为CVr，式中ri为1，rij为样本ij的浓度值比i水平浓度均值的百分比。和线性回归分析类似，精密度分析中，也需要预先设定一个可接受限值。当SDr为CVr超过设定限值时，不能继续进行线性评价，需要找到可能引起精密度差的原因，重新实验后再进行线性评价。和允许误差的事先设定值一样，精密度SDr或CVr应符合企业注册标准的相应要求，而且是不同检测项目和浓度区间依赖的。一般CVr设定为5%，但在高浓度检测区间，可为10%，甚至更高。

2 qIVD产品注册检验线性评价建议方法的应用实例

糖类抗原19-9定量检测试剂盒主要用于定量检测人血清、血浆中的CA19-9含量，可用于胰腺癌的临床辅助诊断。该qIVD产品为定量体外诊断试剂，原理为微孔板双抗体夹心的化学发光免疫分析，属于非竞争性标记免疫分析，为手动加样产品。线性与非线性间允许误差设定为5%，精密度设定为5%。

2.1 试剂盒校准品线性

（1）样本要求：该试剂盒共有6个浓度水平的校准品 （包括零点校准品），每个浓度水平的校准品测定2次，并覆盖企业标准中已声明试剂盒检测的线性范围，为10～500U·mL－1，符合要求。

（2）数据转换：按企业标准方法，对原始数据进行以10为底的双对数转换。原始数据和转换后的数据见表1。

表1 糖类抗原19-9（CA19-9）定量检测试剂盒检测结果

（续表1）

（3）绘制散点图及离群值的发现和处理：通过观察散点图，见图1，可以发现：①经转换后的数据具有明显的线性趋势；②数据的精密度总体较好。由于该数据将进行直线方程的拟合，通过观察发现，该直线明显地不经过原点，即回归方程很可能含截距项。

图1 糖类抗原19-9定量检测试剂盒校准品的对数浓度值 （log10）与对数读数值 （log10）的散点图

（4）线性回归分析：按企业标准声明的直线方程，使 用 Analyse-it软 件 （Analyse-it software，版本：2.3）对转换后的数据进行线性回归拟合。如图2。回归方程的斜率估计值为1.023，截距估计值为4.366，针对斜率和截距的t检验显示两参数均有统计学显著性，回归方程从统计上成立。方程的确定系数R2为0.9979，相关系数r的绝对值为0.9989，符合要求。因此，回归方程为含截距项的直线方程，与通过散点图得出的结论一致。

2.2 利用样本对试剂盒线性的评价

（1）该试剂盒共有6个浓度水平的校准品 （包括零点校准品），每个浓度水平的校准品测定2次，符合相应要求。覆盖企业标准中已声明试剂盒线性范围 （10～500U·mL－1），符合相应要求。

（2）绘制散点图及离群值的发现和处理：通过观察散点图，见图2，可以发现：①数据具有明显的线性趋势；②数据的精密度好。

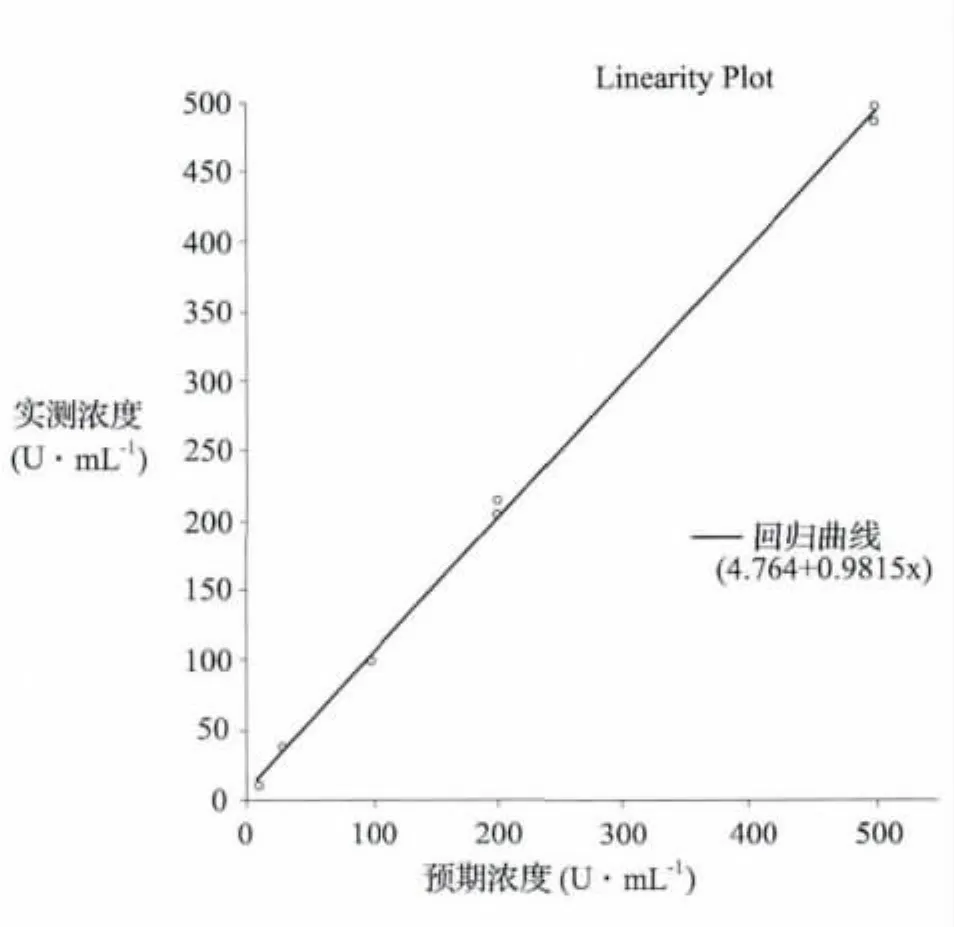
图2 糖类抗原19-9定量检测试剂盒的线性评价样本检测结果的散点图

（3）使用 Analyse-it软件 （Analyse-it software，版本：2.3）分别拟合一次多项式、二次多项式和三次多项式回归方程，软件根据回归曲线参数的统计检验结果和方程标准误给出最优方程，见表2。本数据拟合的最优回归方程为一次多项式 （直线方程），未发现统计学显著的非线性，因此，无需计算非线性回归方程与线性方程待测物浓度预测值的差值。利用样本进行线性评价，显示该试剂盒在10～500U·mL－1呈现线性。

表2 糖类抗原19-9定量检测试剂盒的统计分析结果

（4）精密度：根据数据特点，计算CVr，结果为2.7%，小于预先设定值 （5%）。

为了能更好地应用于实际工作并满足不同的用户需求，从第一版EP6-P使用线性失拟误差 （LOF）评价非线性度，到第三版EP6-A使用线性偏差（DL）评价非线性度，CLSI一直在对指南进行不断的改进。本文所介绍的参考指南EP6-A的建议方法也需在以后根据实际情况加以修正和不断改进。

［1］国家食品药品监督管理局.体外诊断试剂分析性能评估系列指导原则 （征求意见稿）［EB/OL］.（2009-6-01）［2013-07-09］.http：//www.cmde.org.cn/CL0013/795.html.

［2］In vitro diagnostic medical devices-Information supplied by the manufacturer （labelling）-Part 1：Terms，definitions and general requirement［S］.ISO 18113-1：2009，2009.

［3］FDA Recognized Consensus Standards［EB/OL］.（2013-07-09）［2013-07-09 ］. http：//www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfStandards/search.cfm.

［4］核酸扩增检测用试剂 （盒）［S］.YY/T 1182-2010，2010.