基于Taylor实验及理论分析的泡沫铝动态冲击特性研究
2013-09-10庞宝君
庞宝君,郑 伟,陈 勇
(哈尔滨工业大学 航天学院,哈尔滨,150080)
泡沫铝是在纯铝或铝合金中加入添加剂后,经过发泡工艺而成,同时兼有金属和气泡特征,一般情况下泡沫铝以铝合金为基体。泡沫铝因其具有密度小、吸能强、耐高温等优异性能成为一种具有广泛开发前途的工程材料,适用于军事工业的冲击保护层,汽车缓冲器等[1-2]。近些年来随着泡沫铝应用领域不断扩展,国内外研究人员均对其进行了大量研究[3]。刘新让等[4-5]针对泡沫铝的吸能抗爆特性进行了研究。随着泡沫铝研究领域的进一步扩大,有需要了解泡沫铝材料更为详尽的动态力学响应特性,如:高应变率下的动态屈服强度等等。
Taylor[6]实验方法简单、有效,且容易实现大变形、高应变率(104~107/s)以及高温升,也能用于本构方程的校验,成为测量致密金属材料动态响应特性的重要手段,相关理论结果也较为完备。Taylor分析在泡沫金属的应用较晚,国外研究者[7-9]利用Taylor实验来研究泡沫金属(包括泡沫铝)动态响应特性,而国内的陈成军等[10-11]也开展了一部分研究,并进行了Taylor冲击的理论分析工作。本文在Lu等研究基础上,对相关假设加以改进(塑性区相对密度与刚塑性分界面应变的新型函数关系、刚塑性分界面处塑性应变与未变形区长度的变化关系等),并基于Taylor冲击试验数据,参照经典Taylor理论提出了一个泡沫铝Taylor理论分析模型,获得了Taylor实验中泡沫铝动态屈服强度随弹体参数的变化规律,且利用实验数据验证了模型的有效性;得到了泡沫铝子弹变形段平均密度、剩余长度随撞击初始条件的变化情况,为泡沫材料的动态响应测试提供参考。
1 Taylor冲击实验
Taylor实验中,子弹材料为开孔泡沫铝,其基体材料为6061铝合金,由上海众汇泡沫铝材有限公司提供。实验试件均从500 mm×500 mm×25 mm板材上经线切割制成。泡沫铝板材的平均孔径约为1.6 mm,孔隙率在60%~80%之间,Taylor冲击实验试件名义尺寸为Ф12.7mm×60mm,准静态实验试件名义尺寸为Ф25 mm×25 mm。对Taylor实验中的泡沫铝的密度进行测量(见表 1),可知试件平均密度约为0.9 g/cm3。Taylor实验是在哈尔滨工业大学空间碎片高速撞击研究中心的一级气体炮上进行的,子弹撞击速度在40~150 m/s之间。实验中采用激光测速系统获取泡沫铝子弹的速度,刚性靶采用厚度为12.5 mm的A3钢板。实验系统如图1所示,泡沫铝撞击刚性墙见图2。

图1 Taylor实验系统Fig.1 Taylor experiment system

图2 泡沫铝撞击刚性墙示意图Fig.2 Schematic diagram of aluminum foam impact rigid target

表1 Taylor实验结果Tab.1 Result of Taylor experiments
利用高速摄影相机判断泡沫铝子弹的弹道稳定性,图3显示了撞击速度为83 m/s时不同时刻下子弹的飞行状态。高速摄像机型号为FASTCAM SA5,采用帧率为30 000 fps,每33.3 μs采集一次图像。在高速摄影相机两侧安置2个1.2 kw的高压灯为拍摄提供光源以保证拍摄清晰度。不同撞击速度下,泡沫铝子弹最终变形情况如图4所示,实验详细数据如表1所示。

图3 撞击速度v=83 m/s时不同时刻下子弹飞行状态的示意图Fig.3 Schematic diagram of projectile flying state in Different time with impact velocity of 83 m/s
采用哈尔滨工业大学材料学院的INSTRON 5569电子万能材料实验机对泡沫铝试件进行准静态压缩试验,加载速度为5 mm/min,得到工程应力-应变曲线。
由图5可知,泡沫铝应力-应变曲线呈现典型多孔固体材料受压缩时的三阶段特征(弹性段、屈服平台段、密实段),泡沫铝静态屈服强度约为4.0 MPa。

图4 Taylor实验后试件变形情况Fig.4 Specimen deformation after Taylor experiment

图5 泡沫铝的准静态压缩试验曲线Fig.5 Quasi static compression curve of aluminum foam
2 泡沫铝Taylor理论模型
由图2可知,泡沫铝子弹以速度v0撞击刚性墙,子弹撞击靶板之前,弹体横截面面积为A0,密度为ρ0。泡沫铝试件尺寸在平均孔径的7倍以上,可以假定材料是各向同性,且连续均匀。塑性扰动以速度c向试件的自由端进行传播,任意t时刻未变形区域的瞬时速度为v,定义塑性波波后与未变形区域的交接面为刚塑性分界面。为建立泡沫铝的Taylor撞击模型,提出如下假设:① 假定材料为理想刚塑性材料,忽略弹性波效应;② 在撞击过程中,刚塑性分界面处,面积由A0突变为A;③ 弹体在塑性区域的应力保持恒定,与流动应力Y大小一致;④刚塑性分界面处,弹体材料密度由初始密度ρ0变为ρ,且相对密度(ρ与ρ0的比值)仅为刚塑性分界面处塑性应变的函数。
首先,基于质量守恒原理,在任意微小时间段dt内,塑性区材料质量的增加与刚性区质量材料的减少保持一致,即:

对刚塑性分界面上的微元而言,其水平方向上动量平衡,于是有
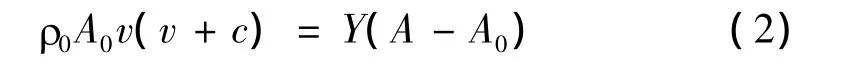
在任意时刻,该微元变形前后的质量保持不变,由此得到任意时刻刚塑性分界面上的工程应变e,即:

联合式(1)、式(3)可得:

根据式(2)~式(4)可以得到:
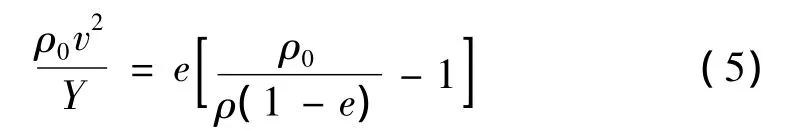
实验完成后采用线切割手段将泡沫铝试件剖开,其剖视图见图6,最终从泡沫铝子弹刚塑性分界面到撞击端,其塑性变形区域的密实情况不断增加。前文假设中,塑性区相对密度仅为分界面处塑性应变的函数,在此进一步假定冲击后塑性区相对密度与e呈指数关系:


图6 冲击后对泡沫铝子弹剖视图Fig.6 Section view of projectile after impact
极限条件下,泡沫铝变形后的最大密度等于6061材料的密度,大小约为2.71 g/cm3;而泡沫铝原始密度约为0.9 g/cm3左右,因此将emax→1带入式(6)可知常数a=2。
参照图2可知,在任意时刻,对泡沫铝子弹有变形方程:
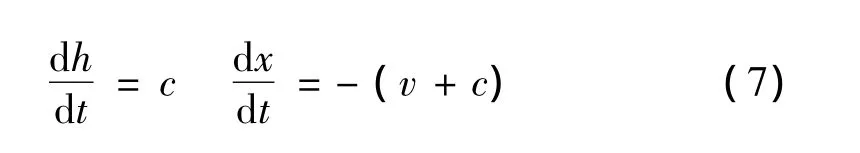
针对子弹的未变形段,有动量方程:

将式(4)代入式(8)中,则有:


将式(10)代入式(9)中,可得:

对式(11)两端积分,并进行整理可知:

在撞击初始时刻,由式(5)可以确定此时的塑性应变e=e0,而此时子弹未变形长度x=L;另外,当子弹开始离开刚性靶板时,刚塑性分界面处塑性应变e=0,假定此时子弹的未变形长度x=X;将以上条件代入式(12),联立求解可以得到:


假定泡沫铝子弹变形段部分的最终长度为H,则有:
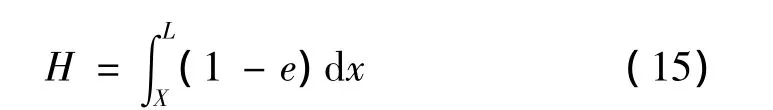
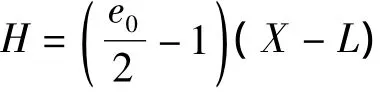
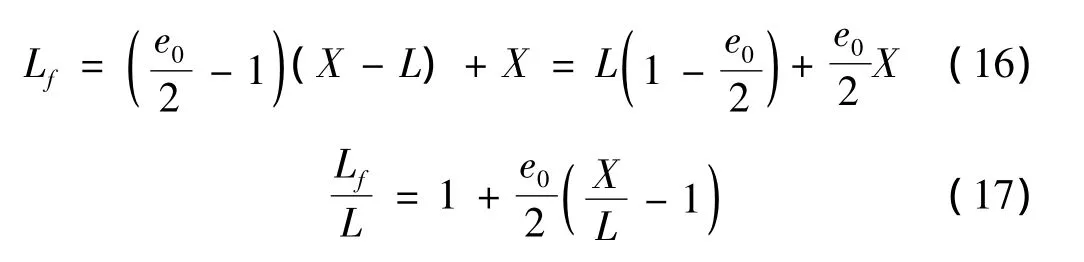
至此得到了泡沫铝Taylor理论分析模型。为便于简化研究,模型中的Y为材料的动态屈服强度,带入子弹初始撞击条件,联合式(5)、式(13)、式(17),基于泡沫铝剩余长度等实验数据,可以预估的泡沫铝动态屈服强度进行预测;另外,将Y取固定的静态屈服强度也可以预测泡沫铝Taylor撞击时弹体剩余长度等参数。
3 泡沫铝实验结果及理论分析
为校核模型的有效性,首先对变形段密度进行分析。利用线切割将实验后的泡沫铝剖成两半,将子弹变形段近似等效为一个圆台,而变形段在实验前为一个圆柱。根据质量守恒原理,通过比较实验前后二者的体积变化情况可以估算出实验后泡沫铝子弹变形段的平均密度。另外,由式(6)可知,子弹变形段密度与界面塑性应变的关系如图7所示;由积分中值定理可以得到变形段平均密度与界面塑性应变关系为:
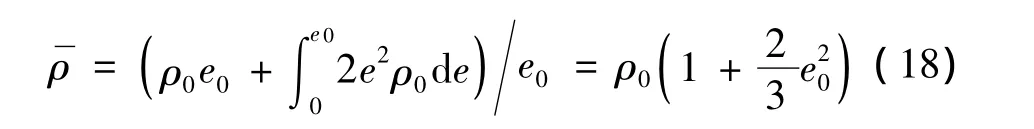
最终实验与理论计算得到的泡沫铝子弹变形段平均密度变化情况如图8所示。由图8可知,理论计算所得到的平均密度与实验测量得到的平均密度值基本吻合,变化规律也基本类似;同时发现,在泡沫铝子弹破碎以前,随着撞击速度的增加,变形段塑性变形加剧,泡沫铝变形段的平均密度也随之增加;且当子弹撞击速度大于110 m/s时,其增长趋于平缓。

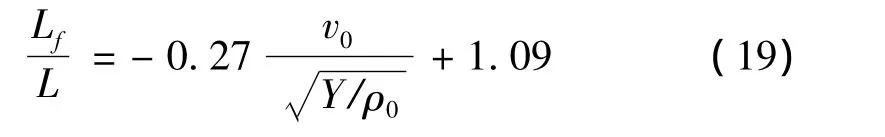
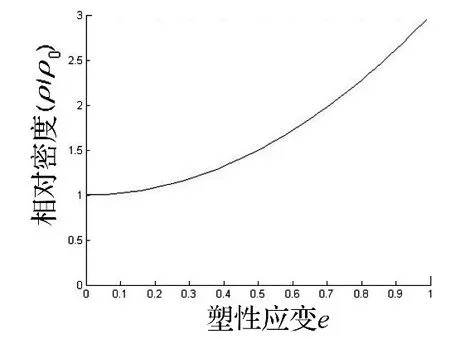
图7 泡沫铝变形段相对密度随界面塑性应变的理论分布Fig.7 The relative density distribution of aluminum foam deformed region with interface plastic strain
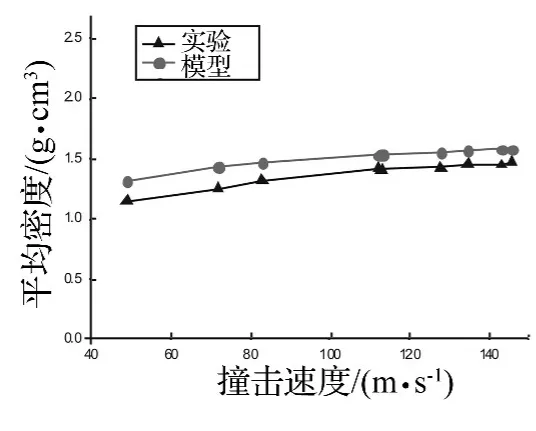
图8 泡沫铝变形段平均密度的变化规律Fig.8 The mean density of aluminum foam deformed region with impact velocity

图9 子弹剩余长度随撞击初始速度的变化规律Fig.9 The residue length of aluminum foam projectile with impact velocity variation
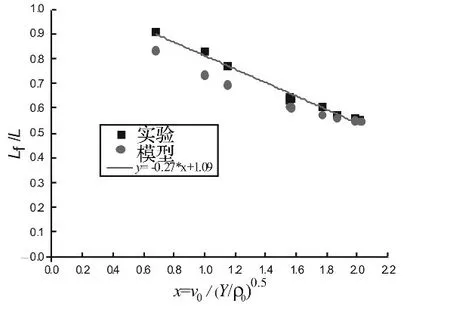
图10 Lf/L 与 v0/之间的关系Fig.10 The relation of Lf/L and v0/
子弹变形段平均密度、子弹剩余长度的理论计算值均较实验值稍大,其主要原因有如下几点:① 理论分析中忽略了弹性波效应;② 理论计算时,将泡沫铝基体的密度作为泡沫铝试件变形段的最大密度,而实际实验中对泡沫铝试件进行冲击压缩并不能将其压实为基体材料,试件的最大密度始终小于基体材料密度,这导致理论计算时a值偏大,使得计算值偏大;③ 撞击变形过程中,相对密度与塑性应变的函数关系与真实情况仍然存在一定的差异;④ 理论计算中为了便于计算,Y直接取静态屈服强度值,而Y实际是指材料的动态屈服强度,与应变率相关,静态屈服强度值较动态屈服强度值小,而Y值的降低也直接导致了e0计算的变大,使得泡沫铝变形段平均密度、泡沫铝试件剩余长度计算值偏大。
4 结论
采用理论分析手段对泡沫铝材料的动态冲击响应特性进行研究,获得了泡沫铝动态屈服强度随弹体参数的变化规律,并基于泡沫铝Taylor冲击实验数据验证了模型的有效性,得到如下结论:
(1)基于一定假设建立的泡沫铝Taylor理论分析模型是有效的,文中相应假设可以为其它泡沫材料Taylor冲击特性的研究提供参考。
(2)在应变率敏感性不高的前提下,泡沫铝Taylor冲击后,子弹变形段平均密度随速度增加而增大,当撞击速度大于110 m/s后,其增长趋于平缓;且子弹剩余长度随撞击速度的增加几乎呈线性减小。
[1]田 杰.泡沫铝的冲击波衰减和抗爆震特性研究[D].合肥:中国科技大学,2006,1-10.
[2] Gibson L J.Mechanical behavior of metallic foams,Annual Review of Materials Science,2000,30:191-227.
[3]卢子兴,郭 宇.金属泡沫材料力学行为的研究概述[J].北京航空航天大学学报,2003,29(11):978-983.
LU Zi-xing, GUO Yu. Brief review of studies on the mechanical behavior of metallic foams[J].Journal of Beijing University of Aeronautics and Astronautics,2003,29(11):978-983.
[4]刘新让,田晓耕,卢天健,等.泡沫铝夹芯圆筒抗爆性能研究[J].振动与冲击,2012,31(23):166-173.
LIU Xin-rang,TIAN Xiao-geng,LU Tian-jian,et al.Blastresistance behaviors of sandwich-walled hollow cylinders with aluminum foam cores[J].Journal of Vibration and Shock,2012,31(23):166-173.
[5]程 涛,向 宇,李 健,等.泡沫铝填充多棱管的吸能分析[J].振动与冲击,2011,30(9):237-242.
CHENG Tao,XIANG Yu,LI Jian,et al.Energy absorption analysis of foamed aluminum-filled prisms[J].Journal of Vibration and Shock,2011,30(9):237-242.
[6]Taylor G I.The use of flat-ended projectiles for determining dynamic yield stress,I:theoretical considerations[J].Proceedings ofRoyalSociety ofLondon,Series A:Mathematical and Physcial Sciences,1948,194(1038):289-300.
[7]Lu G X,Wang B,Zhang T G.Taylor impact test for ductile porous materials-Part 1:theory.International[J].Journal of Impact Engineering,2001,25(10):981-991.
[8]Wang B,Zhang J,Lu G.Taylor impact test for ductile porous materials-Part 2:experiments[J].International Journal of Impact Engineering,2003,28(5):499-511.
[9] Lopatnikov S L,Gama B A,Haque M J.Dynamics of metal foam deformation during taylor cylinder-hopkinson bar impact experiment[J].Composite Structure,2003,61(1-2):61-71.
[10]陈成军,谢若泽,张方举,等.Taylor撞击实验在泡沫铝合金力学特性研究中的应用[J].爆炸与冲击,2008,28(2):166-171.
CHEN Cheng-jun,XIE Ruo-ze,ZHANG Fang-ju,et al.An application of Taylor impact experiment to study mechanical behaviors of an aluminum-alloy foam.Explosion and Shock Waves,2008,28(2):166-171.
[11]卢子兴,赵亚斌,谢若泽.对泡沫铝合金压缩行为及Taylor撞击过程的数值模拟[C]//中国复合材料学会.复合材料:创新与可持续发展(下册)[A].北京:中国科学技术出版社,2010:886-891.
