面向轨道车辆抗蛇行振动的磁流变脂阻尼器设计与台架测试

廖昌荣，赵丹侠，刘 琼

(重庆大学 光电技术及系统教育部重点实验室智能结构中心，重庆 400030)

磁流变液减振器是一种实时调节的阻尼装置，可用于轨道车辆垂向振动控制、横行振动控制、抗蛇行振动控制等领域。石家庄铁道学院［1－2］、西南交通大学［3］、同济大学［4］、香港中文大学［5－6］等都进行了相关研究工作，研究表明磁流变液减振器的可控性能直接影响到控制效果。文献表明:采用混合工作模式/流动模式的磁流变液减振器有效阻尼通道长度短，导致磁场利用率不高;由于磁流变液沉降的问题导致阻尼器控制特性劣化。磁流变脂是由微米级铁磁性粒子、基础油、稠化剂、添加剂和填料组成的结构骨架的胶体分散体系，其流变性能在外磁场作用下能够发生连续可逆变化，不会发生悬浮相沉降与板结问题。鉴于磁流变脂材料进展和传统磁流变液减振器存在的问题，作者提出一种基于多级径向流动模式的磁流变脂阻尼器设计方案。国内外对非牛顿流体径向流动研究的报道相对较少，Livesey［7］研究了粘性流体在两平行圆盘间的径向流动。Jackson等［8］对于平板间的层流流动进行了理论与实验研究。Dai等［9］研究两固定圆盘间的宾汉塑性流体的径向流动的数值解。目前，还未见关于径向流动模式的磁流变脂阻尼器设计理论报道，深入研究多级径向流动模式磁流变脂阻尼器设计方法，对磁流变脂阻尼调节装置的工程化研究具有重要的学术意义和潜在的实用价值。

1 基于多级径向流动模式的磁流变脂阻尼器

如图1所示的磁流变脂阻尼器，在外力作用下活塞迫使工作缸中的磁流变脂在阻尼调节器中往复流动，若忽略密封摩擦压力差和磁流变脂流动损失压力差，工作缸左右两腔之间压力差主要由阻尼调节器中磁流变脂流动特性决定。通过改变线圈励磁电流来控制通道磁场强度，以改变磁流变脂的流动特性，实现阻尼调节的目的。

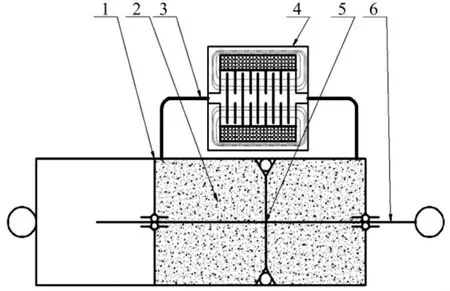
图1 基于多级径向流动模式的磁流变脂阻尼器Fig.1 MR grease damper based on multi radial flow mode

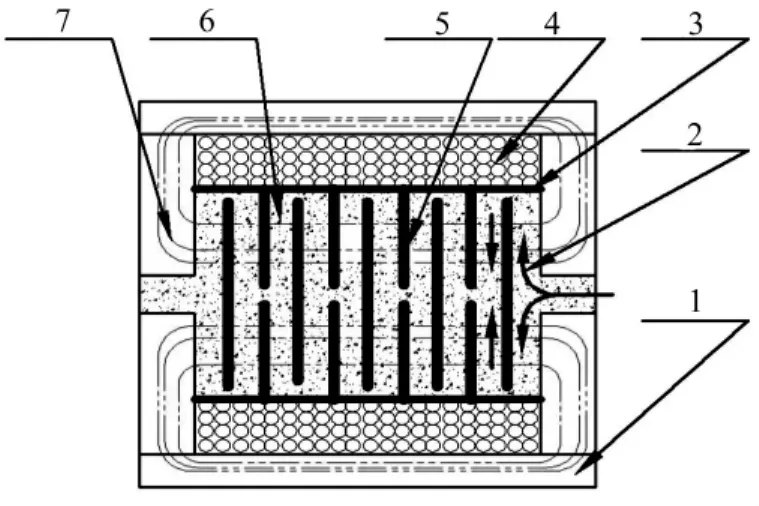
图2 阻尼调节器结构Fig.2 Illustration showing damping adjuster

多级导磁隔板、不导磁钢筒、励磁线圈、导磁端盖和导磁外筒等组成如图2所示阻尼调节器，流经调节器的磁流变脂在活塞推动下发生相应的轴向流动与径向汇流，在工作缸左右两腔之间形成压力差。磁流变脂在径向流动区域中流动方向与磁场方向垂直，使磁流变脂的流动特性调节明显，是论文研究的关键。

2 磁流变脂尊静态径向流动模型

2.1 磁流变脂径向流动微分方程

磁流变脂的径向流动存在两种情况:磁流变脂从分级隔板中心的孔向四周径向流出(源流)，磁流变脂从四周径向地汇入中心的油孔(汇流)，阻尼调节器的每一级可看成是源流与汇流的对称组合。建立如图3所示坐标系，r为径向坐标，z为纵坐标，o为原点。环状分级隔板的外径为r2，环状分级隔板的内孔半径为r1，两隔板间距为2h。

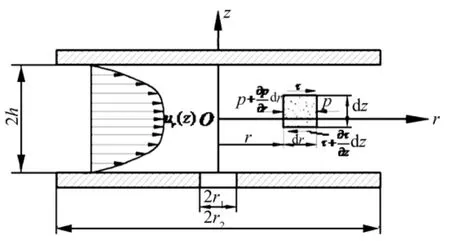
图3 磁流变液径向流动分析模型Fig.3 Model for MR greases radial flow

鉴于磁流变脂在圆盘之间的流动特性和通道结构特点，论文做出如下假设:磁流变脂是不可压缩的;磁流变脂不存在周向流动和轴向流动;鉴于活塞杆运动速度低，磁流变脂流动的雷诺数小，假定磁流变脂在通道中呈层流状态;励磁磁场在径向通道中是均匀分布的;磁流变脂径向压力梯度沿厚度方向成均匀分布。根据磁流变脂在调节器径向通道中流动特征，建立微单元的径向力平衡方程，化简后得到:

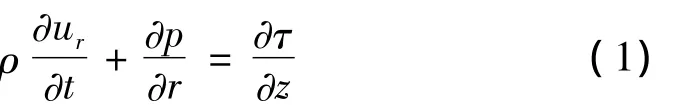
式中:ρ为磁流变脂的密度;ur为磁流变脂在径向的流动速度;τ为磁流变脂受到的剪切应力，t为时间变量，p为径向压力。由于抗蛇行磁流变脂减振器激励速度低，忽略磁流变脂流动的惯性，简化控制方程

2.2 磁流变脂的本构关系模型

磁流变脂本构方程可用双粘度模型来表述:

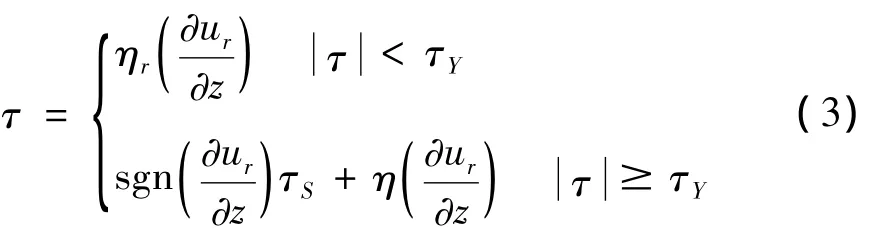
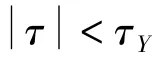
对重庆仪表材料研究所提供的磁流变脂材料进行了流变学特性测试，得出本构关系曲线如图4所示，由实验得出磁流变脂的模型参数与磁通密度B的关系(4)。

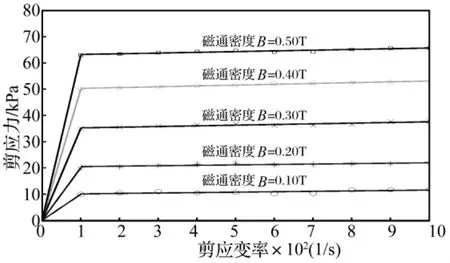
图4 磁流变脂材料的本构模型Fig.4 MR grease bi-viscous constitutive model

3 磁流变脂准稳态径向流动特性

3.1 区域划分

对微分方程(2)积分，注意到对称性边界条件:τ(0)=0:

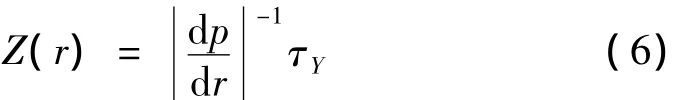
3.2 牛顿流动区

由流体连续原理和磁流变脂无压缩特性，任意半径处的体积流量表示为Q:

从式(7)可知，要确保在任何半径都要满足式(7)，要求积分函数与半径坐标无关，则有:

式中:g(z)为关于纵坐标 z的函数，与半径坐标 r无关。

将式(8)代入本构方程(3)，结合表达式式(5)，再求导得:

对式(9)进行两次积分，考虑到无滑动边界条件ur(－h)=0，得出g(－h)=0，则有:

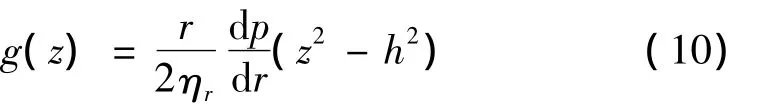
将式(10)代入式(8)，再代入式(7)，得压力梯度表达式:

将式(11)代入式(10)，再代入式(8)，得出牛顿流动区域的径向速度分布函数:

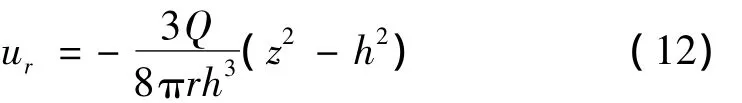
将式(11)代入式(5)得出牛顿流动区域的剪切应力分布函数:

3.3 宾汉流动与牛顿流动共存区域

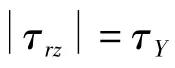
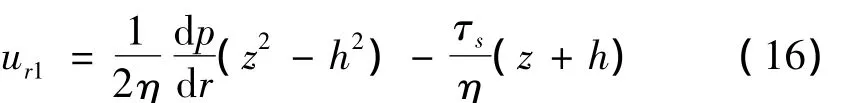
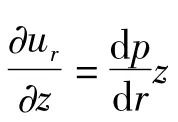
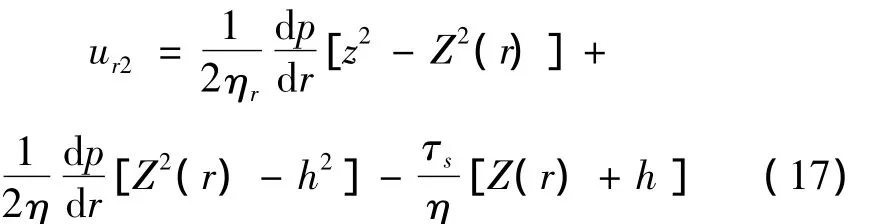
将式(16)、式(17)代入式(7)，化简可得:

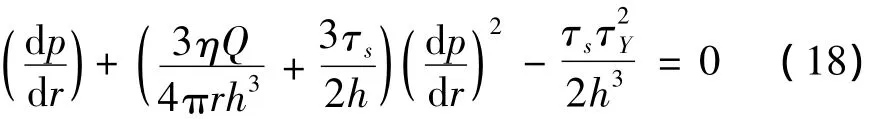
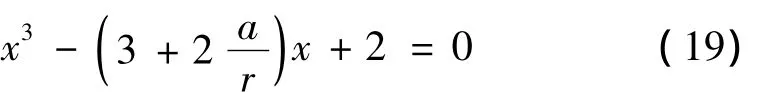
解方程式(19)得:

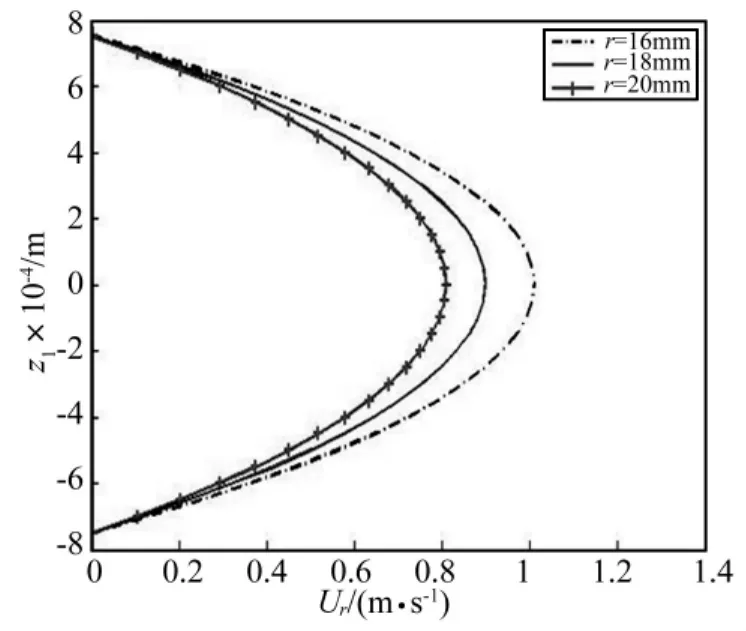
图5(a) 牛顿区域径向速度分布Fig.5(a)Radial velocity profile in Newtown region

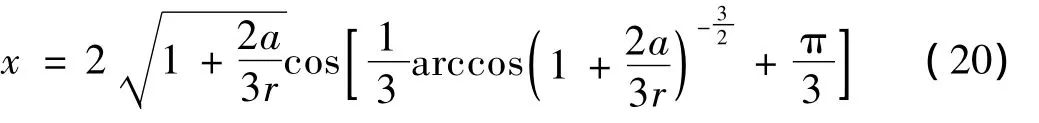
将式(20)中设定参数代入可得压力梯度表达式

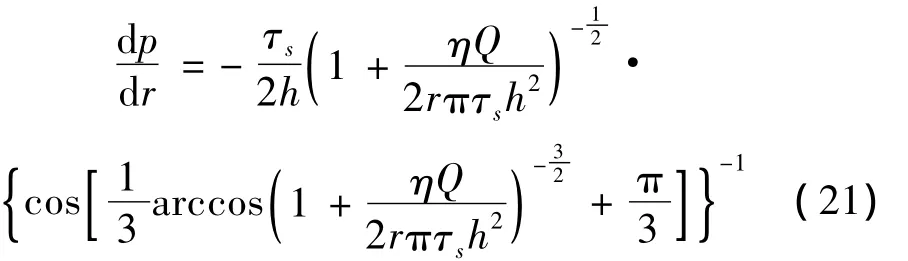
3.4 磁流变脂径向流动速度特征

工作缸活塞速度v0=0.025 m/s，磁流变脂的动态屈服强度τY=30 kPa，由方程(14)可得区域分界半径R0=15.7 mm。将参数代入式(12)可得牛顿流动区域磁流变脂在不同半径坐标处径向速度分布;将参数代入式(19)和式(20)可得共存区域磁流变脂在不同半径坐标处径向速度分布。图5(a)为半径16 mm、18 mm、20 mm处磁流变脂在牛顿流动区域的径向速度的分布图。从图中可以发现，随着半径的增大，径向速度在减小，与实际情况相符。图5(b)则为半径8 mm、10 mm、12 mm处混合流动区域的径向速度分布图。从图中发现随着半径的增大，径向速度减小，屈服区与未屈服区的速度变化相差较大，在屈服区内剪切率比较大，在未屈服区内剪切率相对来说要小得多。为了更全面的了解径向速度变化趋势，作者研究了磁流变脂流动速度的三维曲线图，如图5所示。图6(a)所示牛顿流动区域的三维速度分布图，图6(b)所示为宾汉流动区域的三维速度分布图。从图中能发现在牛顿区域和混合区域都是随着半径的增加径向速度都减小。在双粘度流体区域速度减小的趋势明显高于在牛顿流体区域，越远离分界半径流动速度变化的趋势越明显。从纵坐标方向看，在宾汉流动速度的变化趋势也明显高于牛顿区域流动速度。

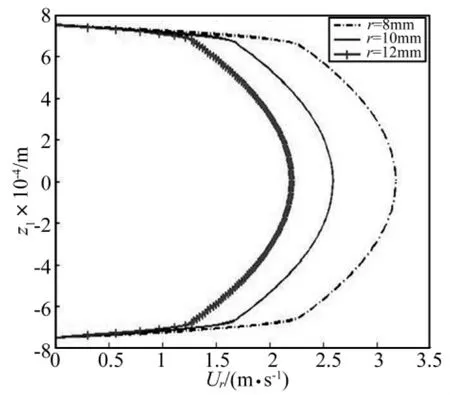
图5(b) 混合区域径向速度分布Fig.5(b)Radial velocity profile in mixed region

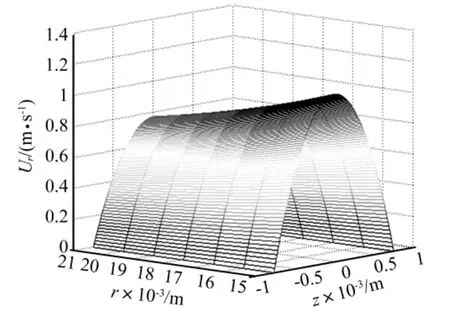
图6(a) 牛顿区域径向速度分布Fig.6(a)radial velocity profile in Newtown region

3.5 磁流变脂阻尼器的阻尼力计算方法

从分析中可知，磁流变脂流动压力差可从牛顿区域和混合区域分别计算。

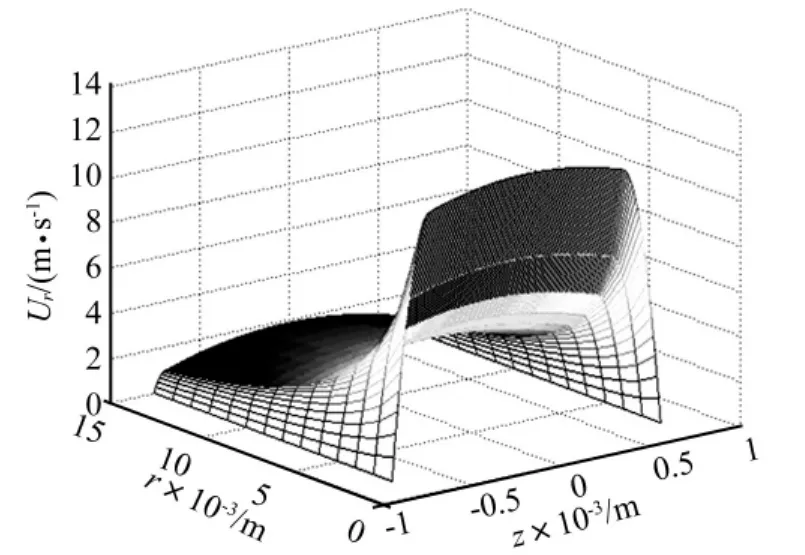
图6(b) 混合区域径向速度分布Fig.6(b)radial velocity profile in mixed region

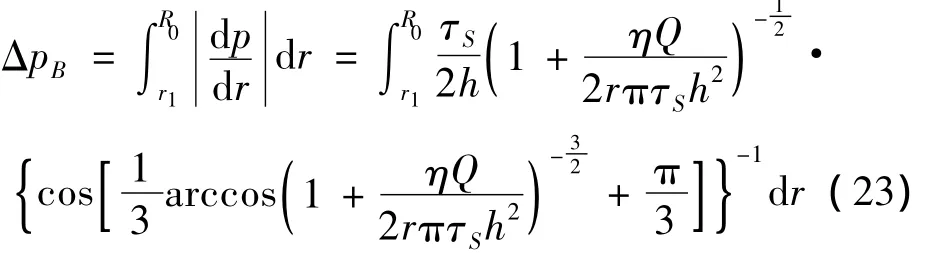
从表达式(23)中的被积函数不能得出其原函数，只有采用数值积分方法。若阻尼通道的级数为N，活塞作用面积为A，磁流变脂阻尼器的阻尼力表示为:

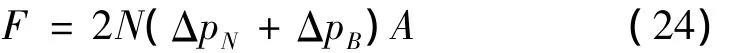
为了得出阻尼通道中的磁通密度与励磁电流的关系，采用电磁场中有限元方法对调节器通道中的磁通密度进行了有限元分析，得出如图7所示的结果，从图中可以看出阻尼通道中的磁场分布是均匀的，利用有限元得出的磁通密度数据，得出励磁电流I与磁通密度B的关系。

将励磁电流代入(25)式得到阻尼通道中的磁通密度，再将磁通密度代入表达式(4)得到磁流变脂的流变学模型参数。将工作缸结构参数和阻尼调节器的结构参数条件下，表达式(22)和式(23)分别得出混合流动区域的压力差和牛顿流动区域的压力差，通过式(24)得出规定激励速度下的阻尼力。

图7 不同励磁电流下的通道中的磁感应强度分布Fig.7 magnetic flux density distribution under various currents

4 磁流变脂阻尼器试验与数据分析

按照轨道车辆抗蛇行减振器的技术要求和安装条件，利用重庆仪表材料研究所提供的磁流变脂材料，设计制作了轨道车辆抗蛇行减振器器(工作缸参数:活塞直径80 mm，活塞杆直径30 mm;调节器参数:级数6，隔板间隙1.5 mm，隔板有效直径100 mm)，如图8所示。按照CRH1动车抗蛇行减振器测试规范，在铁路减振器专用的试验设备J95－1型油压减振器试验台上对抗蛇行磁流变脂阻尼器进行示功特性测试，如图9所示。

图8 磁流变脂阻尼器Fig.8 MR Grease damper

图9 磁流变脂阻尼器测试现场Fig.9 Test site for MR grease damper

磁流变脂减振器测试采用正弦激励，振幅为±25 mm，活塞峰值速度为0.025 m/s，励磁电流取值为:0.2 A、0.4 A、0.6 A、0.8 A、1.0 A，减振器试验台 J95 －1 自动记录磁流变脂减振器的阻尼力与其对应活塞位移参数，绘制出示功特性曲线如图10所示(图中用黑色线表示)。通过(24)式得出规定激励速度下的阻尼力，绘制出理论示功特性曲线如图10所示(图中用蓝色线表示)。从图(10)中可以看出，磁流变脂阻尼器的理论示功特性与实验示功特性有较好的吻合，其能量耗散(示功曲线包围的面积)相差均小于15%。

图10 磁流变脂阻尼器示功特性Fig.10 damping force vs.piston displacement of MR grease damper

在振幅不变的条件下测试了峰值速度为0.01 m/s，0.1 m/s和 0.2 m/s的示功特性。实验表明，三种峰值速度激励下，磁流变脂减振器实验示功曲线包含的面积与理论示功曲线包含的面积相比，误差分别小于 8.9%，20.3%和 23.6%。

磁流变脂阻尼器的理论阻尼值与实验阻尼值存在着较大的误差，其主要原因在于:磁流变脂的流变学特性测试误差;采用的分析模型没有考虑惯性效应的影响，在实际运用中磁流变脂的惯性是不可避免的;没有考虑磁流变脂与隔板之间的滑动效应，在实际的磁流变脂减振器中，磁流变脂与隔板之间的滑动难以预测;没有考虑活塞杆与密封件之间的摩擦;没有考虑磁路非线性导致有效磁通密度降低和磁流变脂动态磁学特性;仅考虑磁流变脂的理想层流状态，实际的流动存在紊流状态的。

5 结论

论文提出了多级径向流动模式磁流变脂阻尼器结构，将建立了准静态径向流动分析模型，利用不滑动边界条件和流动相容条件得出了磁流变脂径向流动下的径向流动特性以及压力分布，得到了理论阻尼力计算方法，并开展了磁流变脂减振器示功特性测试，得出下列结论:

(1)理论径向速度分布其随着隔板半径的增大而减小，符合磁流变脂径向流动实际情况，说明分析模型是合理的。

(2)试验示功特性与理论示功特性能较好吻合，说明磁流变脂的模型参数辨识可靠，用模型得到的压力梯度分布来计算磁流变脂的阻尼特性是合理的。

(3)关于磁流变脂在径向通道中流动的边缘滑动效应、惯性效应和非层流特性问题，需要进行深入研究，进一步完善设计理论。

［1］高国生，杨绍普，郭京波.基于磁流变阻尼器的机车横向悬挂半主动控制研究［J］.功能材料，2006，37(5):802－804.

GAO Guo-sheng，YANG Shao-pu，GUO Jing-bo，Investigation and semi-active control of a lateral suspension systems to locomotive via MR damper［J］. JournalofFunctional Materials，2006，37(5):802 －804.

［2］高国生，杨绍普，陈恩利，等，高速机车悬架系统磁流变阻尼器试验建模与半主动控制［J］.机械工程学报，2004，40(10):87－91.GAO Guo-shen， YANG Shao-pu， CHEN En-lietal.Experimental modeling and application for semi-active control high speed train suspension system［J］.Chinese Journal of Mechanical Engineering，2004，40(10):87－91.

［3］倪平涛，王开文，陈 健，等.抗蛇行减振器对磁流变耦合轮对车辆的临界速度与高速曲线通过性能的影响［J］.铁道学报，2007，29(3):34－39.

NI Ping-tao，WANG Kai-wen，CHEN Jian，et al.，Influence of anti-hunting damper on critical velocity and high speed curve negotiating performance of the vehicle with MRF coupled wheel-sets［J］.Journal of The China Railway Society，2007，29(3):34－39.

［4］陆正刚，胡用生.基于磁流变阻尼器的铁道车辆结构振动半主动控制［J］.机械工程学报，2006，42(8):95－100.

LU Zheng-gang，HU Yong-sheng， Semi-activecontrolof railway vehicle structure vibration based on MR damper［J］.Chinese Journal of Mechanical Engineering，2006，42(8):95－100.

［5］Lau Y K，Liao W H.Design and analysis of magnetorheological dampers for train suspension［J］.Proceedings of the Institution of Mechanical Engineers(Part F，Journal of rail and rapid transit)，2005，219(F4):261－277.

［6］ Liao W H.Semi-active vibration control of train suspension systems via magnetorheologicaldampers［J］.Journalof Intelligent Material Systems and Structures，2003，14(3):161－172.

［7］ Livesey J L.Inertia effects in viscous flows［J］.International Journal of Mechanical Sciences，1960，1(1):84 －88.

［8］ Jackson J D，Symmons G R.An investigation of laminar radial flow between two parallel discs［J］.Applied Scientific Research，1964，15(1):59 －75.

［9］ Dai G，Bird R B.Radial flow of a Bingham fluid between two fixed circular disks［J］.J.Non-Newtonian Fluid Mech.，1981，35(8):349－355.