基于经验模态分解的载货汽车载荷动态检测策略研究

田晶晶，李世武，苏 建，杨志发，陈 璐，汪海正

(吉林大学 交通学院，长春 130022)

车辆的装载状态对其操纵稳定性有重要的影响，车辆行驶过程中装载状态实时动态监测预警可有效预防由异常车辆装载状态诱发的道路交通事故的发生。目前，车辆装载状态分析测量方法大都是离线分析，对载荷动态检测的方法研究较少。Niedzwiecki［1］研究自适应滤波法在车辆动态称重的应用。郭兰英等［2-3］研究了应变式轴重秤，它们主要应用于车辆载重量的检测站称重检查。陈广华等［4］设计了基于粘贴式应变传感器的车辆超载监测系统，但该系统中车辆载荷检测传感器结构复杂、成本高，因此实用性较差。

根据汽车理论的相关背景知识，悬架是整车悬挂质量的承载构件，其最主要的功能是传递作用在轮胎和车架之间的力和力矩，缓和路面不平度对车辆的冲击并衰减由此引起的车辆振动。首先本文仿真分析了钢板弹簧悬架的动态力学特性。基于车辆载荷与悬架钢板弹簧变形量的关系分析结果，设计了一种高精度带过载保护的汽车载荷动态检测装置［5］，并构建了车辆载荷检测动态系统试验平台。

1 悬架动力学特性仿真分析

1.1 路面不平度模型

路面不平度是车辆行驶过程中最主要的激励源之一。根据长春汽车研究所制订的《车辆振动输入—路面不平度表示方法》(GB/T7031-1986)将路面不平度将路面分为A～H级［6］。目前我国路面以B级路面为主，本文以B等级路面不平度激励作为车辆振动模型的输入激励。参考文献［7］，建立路面不平度随机激励信号生成的数学模型，如式(1)所示:

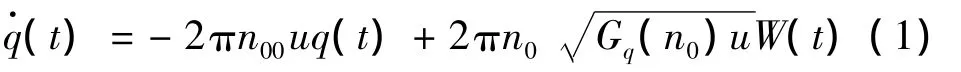
式中:n00为下截止空间频率，n00=0.011m-1;n0为参考空间频率，n0=0.1m-1;Gq(n0)为路面不平度系数，m3;W(t)为均值为零的高斯白噪声;q(t)为路面随机高程位移，m。

1.2 二自由度悬架动力学模型

本文以解放赛龙ⅡCA1169PK2L2EA80载货汽车为试验车。根据其结构特性选用二自由度四参数1/4车辆悬架动力学模型，悬架的简化结构如图1。

图1 1/4车辆悬架结构模型Fig.1 Structure model of suspension of a quarter vehicle

车辆悬架动力学微分方程如式(2)所示:

式(2)的状态向量为式(3):

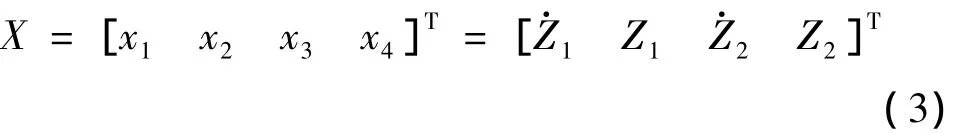
输入向量为:

输出向量为:

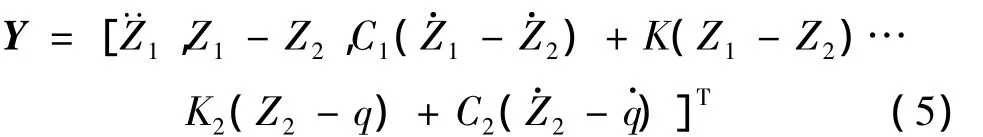
将式(3)～(5)代入式(2)得式(6):

式(6)系数矩阵A、B、C、D分别为:

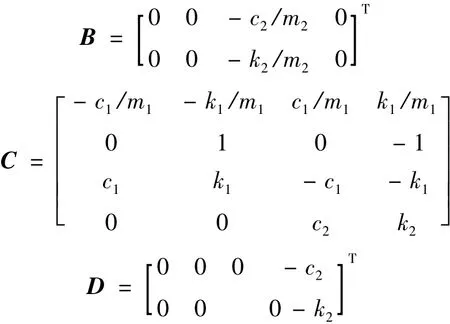
1.3 仿真分析

根据选定的试验车型，车辆悬架建模参数如表1所示。

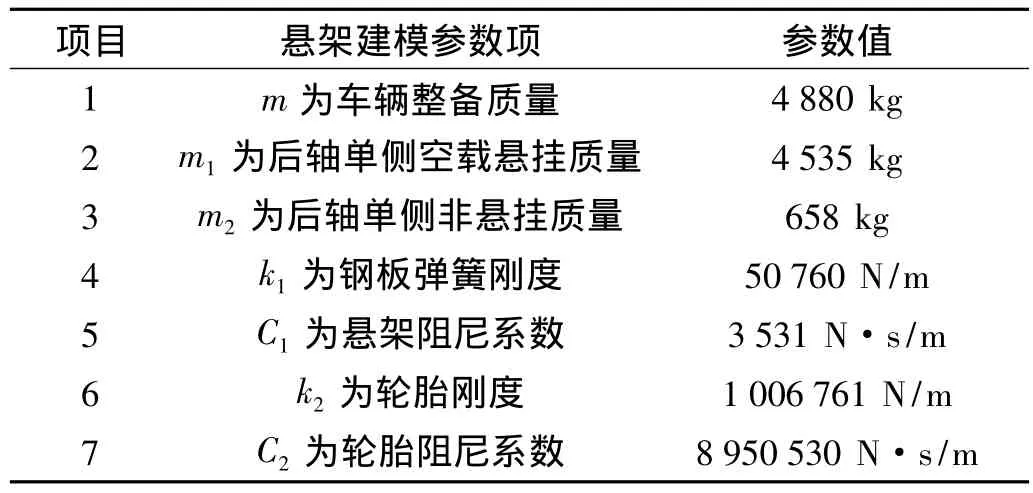
表1 车辆建模参数Tab.1 Parameters of vehicle modeling

在Matlab/Simulink环境中［8］建立车辆悬架动力学仿真模型，对车辆在B等级路面、车速30 km/h和60 km/h、半载状态下悬架的动态特性进行仿真分析。根据图2不同车速下悬架的动态载荷可得车速为30 km/h时动态载荷幅值为静态载荷的10%，而且随着车速增加到60 km/h时悬架的动态载荷明显增大［9］。

图2 不同车速下的动态载荷Fig.2 Dynamic suspension load under different speeds

以车辆在30 km/h车速、半载状态运行为例，悬架位移和悬架载荷在路面不平度激励q输入下的幅频域特性曲线，曲线均具有2个峰值，表明该信号为两个不同频率的信号叠加求得，如图3所示。

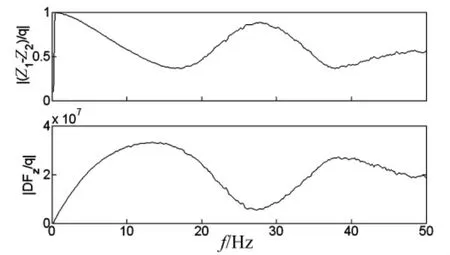
图3 悬架变形量和载荷的幅频特性Fig.3 Magnitude-frequency characteristics of suspension deformation and load

2 车辆载荷动态检测装置

2.1 车辆载荷与钢板弹簧位移量关系

对于特定的钢板弹簧，其刚度系数、弯曲跨距和板簧厚度都是固定值，车辆载荷m和钢板弹簧形变量关系［4］如式(7)和式(8):

其中:α为钢板弹簧相关系数;Δε为钢板弹簧表面应变;l为钢板弹簧跨距，mm;k为钢板弹簧刚度，N/mm;h为钢板弹簧厚度，mm。通过式(7)和(8)推导出车辆载荷与钢板弹簧应变之间存在线性关系。本文通过4.2节系统静态标定试验获取车辆载荷与钢板弹簧变形量之间的映射关系式(24)证明了车辆载荷与钢板弹簧变形量之间的线性关系。

2.2 车辆载荷动态检测装置

基于车辆载荷与钢板弹簧变形量之间的线性关系，本文设计了一种高精带过载保护的汽车载荷动态检测装置，其整体结构如图4(a)所示，由1车体连接板、2拉线式位移传感器、4和5组成的过载保护机构总成、3、15和16组成的过载保护机构锁紧装置和18钢板弹簧连接板组成［5］。本文设计开发的悬架载荷动态检测装置的工作原理如下:拉线式位移传感器2的拉线通过过载保护机构总成的滑轮4由螺栓3固结于车体连接板1，车体连接板1与车架相连;过载保护机构总成通过锁紧装置固结于钢板弹簧连接板18，钢板弹簧连接板估计与钢板弹簧。图4(b)为过载保护机构总成拆解图，主要由滑轮4、导轨12、滑道13和过载保护弹簧9组成。导轨12和滑道13为套装且具有间隙配合的圆柱形管道，滑道13具有卡销调整孔14，过载保护弹簧9套装与导轨12的圆柱形管道内，过载保护弹簧9及导轨12的一端通过螺栓6、7和8固结于滑轮4，另一端通过卡销调整孔15的卡销螺栓11调整过载保护弹簧9的预紧力。滑轮4用于将拉线式位移传感器2输出电压信号加倍，提高传感器测量的精度。

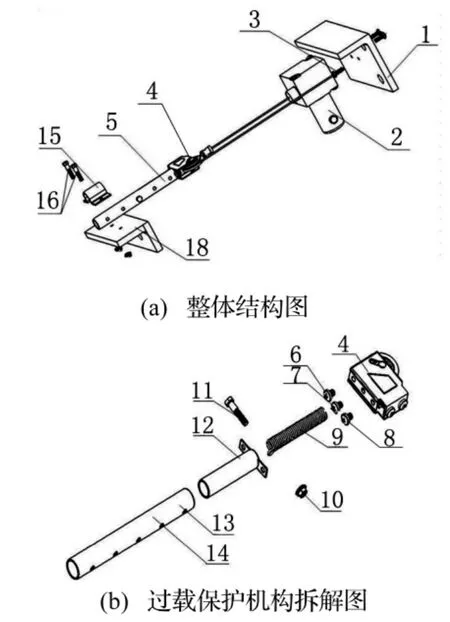
图4 载荷动态检测装置Fig.4 Dymamic detection device for vehicle load

3 基于EMD数据处理算法

3.1 EMD在汽车载荷检测中的应用

EMD是一种基于信号局部特征的分解方法，它将信号分解为若干个本征模态函数(IMFs)和一个残余量，其中IMFs反映了信号的动态特性，残余量反映了信号的趋势或均值。汽车行驶过程中，汽车本身的因素如发动机转动、轮胎与地面摩擦、汽车与路面耦合、路面不平整等因素引起车辆振动而形成动态载荷，车辆行驶过程中载荷状态由静态载荷和动态载荷组成。通过数字滤波不能有效分离静态载荷与动态载荷［10］。本文将汽车静态轴重看作信号的残余量，动态载荷看作信号中的本征模态函数，通过经验模态分解的方法从载荷信号中分离出动态载荷，得到汽车的静态载荷。

3.2 EMD载荷信号处理算法

EMD方法基于以下假设:任何复杂的信号都是由若干个本征模态函数和残余量组成的，每个本征模态函数可以是线性的和平稳的或非线性的和非平稳的［11-12］。EMD方法采用“筛”选的方法从原始信号中将本征模态函数分离出来。本文采用EMD处理位移传感器输出电信号的具体步骤如下:

① 找出位移传感器输出原始电信号x(t)的局部极大值点emax(t)和局部极小值点emin(t)，分别将局部极大值点和极小值进行三次样条插值得到信号的上包络线mmax(t)和下包络线mmin(t)。求出mmax(t)和mmin(t)的均值，求得到原始信号的均值包络线m(t):

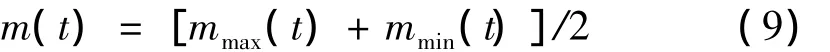
将位移传感器输出原始电信号x(t)与均值包络线m(t)相减，得到第一个分量h1(t)。即:

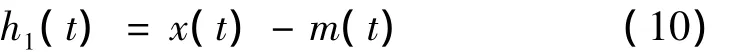
② 检查h1(t)是否符合IMF定义的EMD终止条件(见3.3.1节)。如果h1(t)不能同时满足IMF定义的EMD终止条件，则令x(t)=h1(t)，转步骤1，得到h2(t)，即:

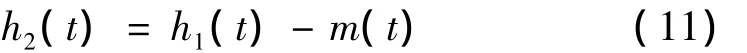
这样经过k次“筛”选得:

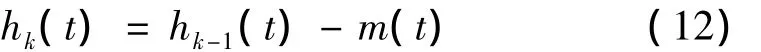
直到hk(t)同时满足IMF定义EMD终止条件，此时得到第一阶IMF分量c1(t)，即:

③ 将位移传感器输出原始电信号x(t)减去第一阶IMF分量可得到剩余量r1(t)，即:

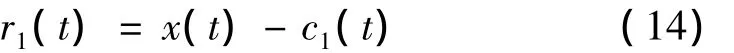
令新信号x(t)=r1(t)，重复步骤①和②，得到第二阶IMF分量c2(t)，再令:

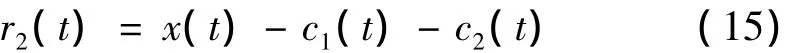
这样继续分解，直至第n阶分量rn(t)小于预先设定的值或rn(t)己经成为单调函数时分解结束。这样位移传感器输出原始电信号x(t)可以表示成n个IMF分量和一个平均趋势分量rn(t)的和，即:

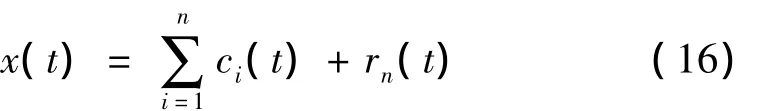
④ EMD分解正交性检查:具有正交性的信号分解方法可以将噪声信息互不干扰地、独立地提取出来。在数学上，如果函数y1(t)和y2(t)满足:

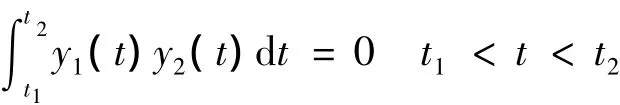
将式(16)写成式(17):

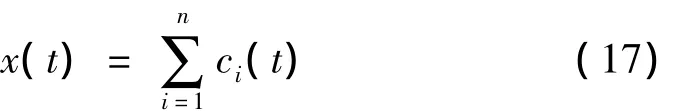
即把平均趋势分量rn(t)看作第n+1个分量cn+1(t)。然后对信号x(t)做平方得:

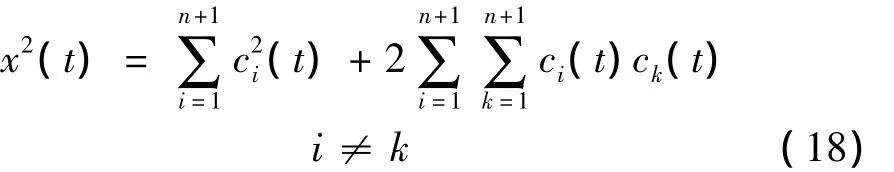
EMD正交性定义到任意两个本征模态函数ci(t)和ck(t)上，其正交性表示为:

3.3 EMD载荷信号处理算法中几个关键问题

3.3.1 EMD 及其“筛”过程终止条件

EMD将原始信号分解为若干个本征模态函数和一个残余量。本文利用EMD方法对位移传感器输出电压信号进行实时分解，基于实时性的要求设定EMD终止条件为:① 位移传感器输出电信号x(t)的极大值点emax(t)和极小值点emin(t)个数之和小于3;② IMF的个数小于5;

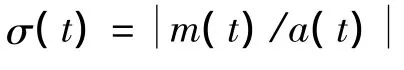
3.3.2 EMD 端点效应抑制

针对EMD法端点效应问题，采用镜像延拓法抑制位移传感器输出原始信号EMD端点效应，并以左延拓信号开始先出现极大值点后出现极小值点为例对镜像延拓法进行分析［2］，其它情况依似类推。设位移传感器输出原始电信号时间序列及其对应的信号序列分别为:

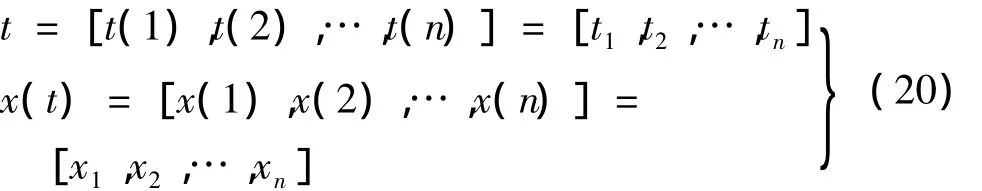
其采样步长为1，x(t)有M个极大值和N个极小值，对应的序列下标(Im，In)、时间序列为(Tm，Tn)，传感器信号值为(U，V):

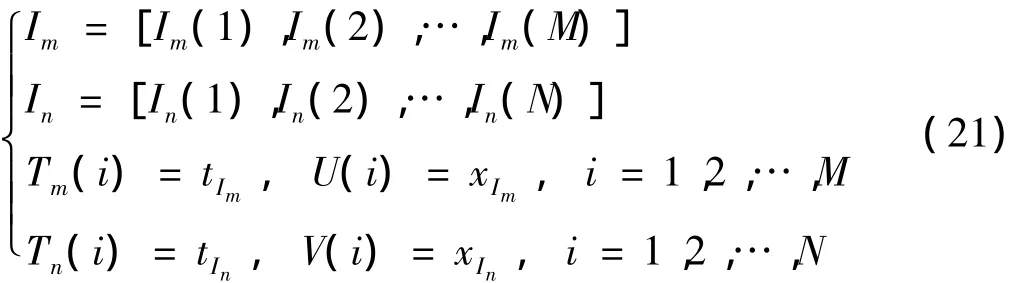
信号开始先出现极大值点后出现极小值点，即Im(1)＜In(1)时，将信号端点的镜像延拓分为以下两种情况:

(1)如果左端点的数值比第一个极小值点In(1)的值大，即x(1)＞V(1)，则以极大值点Im(1)作为对称中心向左延拓，得到两个极值的位置(Tm，Tn)和数值(U，V)为:

(2)如果左端点的数值小于或等于第一个极小值In(1)，即x(1)≤V(1)。此时将左端点定义为第一个极小值点，以左端点为对称中心向左延拓，得到两个极值的位置(Tm，Tn)和数值(U，V)为:

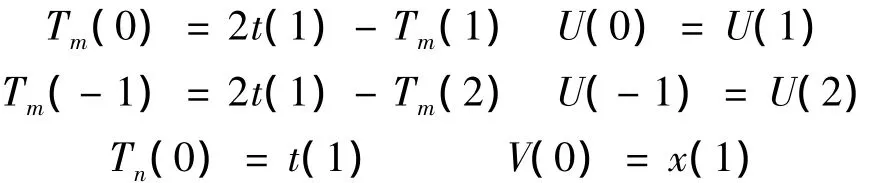
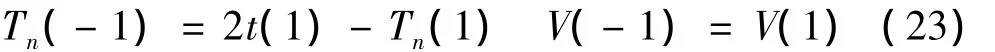
4 车辆载荷动态检测试验

4.1 载荷动态检测系统构建

本文以解放赛龙Ⅱ载货汽车为试验车、悬架载荷动态检测装置、Freescale的MC9S12XEP100单片机为车载终端构建车辆载荷动态检测系统试验平台［14］，分别如图5中1、2和3所示。

图5 车辆载荷动态检测试验平台Fig.5 Platform for dynamic detection of vehicle load

车载终端以10 Hz的采样频率获取悬架载荷检测装置中位移传感器输出电信号。基于传感器输出电信号的EMD处理算法，车载终端采集、处理、计算车辆载荷状态信息的流程如图6所示。

4.2 载荷动态检测装置标定试验

本文通过车辆载荷动态检测装置静态标定试验获取悬架载荷与钢板弹簧变形量的关系。系统静态标定试验在一汽农安汽车试验加载场区进行，试验过程如图5中4所示，试验车以500 kg载重间隔添加砝码，装卸两次分别利用CAS称重仪(见图5中1的标记处)测量四组轮胎的垂直载荷，车载终端(见图5中3)采集对应载荷下的四组位移传感器的输出电压值。砝码的总加载量为15 T，超过车辆的额定载荷50%。通过系统静态标定试验获取四组悬架载荷与对应的位移传感器的输出电信号之间的对应关系，分别如式(24)所示:

图6 车载终端工作流程Fig.6 Workflow of vehicle

其中:Ffl，Ffr，Frl，Frr为车辆左前、左后、后左和后右侧车辆载荷与钢板弹簧变形量的对应关系。

4.3 车辆载荷动态检测试验

图7 40、60和90 km/h时，不同装载量时载荷检测Fig.7 Dynamic detection of vehicle load status under different loading with 40、60 和 90 km/h

为验证系统在车辆行驶过程中对车辆载荷的动态测量结果的准确性，本文在一汽农安汽车试验场性能路进行了车辆载荷动态检测试验，在40，60和90 km/h车速下、对车辆装载量为空载、半载和满载时进行动态检测。图7(a)和(b)为车辆载荷检测装置在车速为40和60 km/h车速和空载、半载和满载的装载量下对其载质量动态检测值的波动状态，车辆装载量为半载时，系统检测误差最大，系统检测误差均小于5.0%。图7(c)为车辆载荷检测装置在车速为90 km/h车速和空载、半载和满载的装载量下对其载质量动态检测值的波动状态，车辆满载时检测误差分别为 3.12%，7.616%和6.75%。由此可见，该装置随着车速增大检测误差增大。

5 结论

针对载货汽车载荷动态检测问题，首先通过二自由度1/4车辆振动模型仿真分析了悬架的动态特性;然后基于仿真分析得悬架载荷与变形量的对应关系，设计开发了一种高精度带过载保护的载荷检测装置，并采用EMD法构建了车辆载荷检测装置输出信号数据处理模型;最后以解放赛龙Ⅱ重型载货汽车为试验车、MC9S12XEP100单片机为车载终端设计开发了车辆载荷状态动态检测试验平台。在一汽农安汽车试验场进行了系统静态标定试验，得出悬架载荷与变形量的映射关系方程，车辆分别在空载、半载和满载状态下，以40、60和90 km/h车速行驶进行载荷动态检测试验，试验结果表明该方法可以准确检测对车辆40和60 km/h车速行驶时载荷进行动态检测，检测误差不超过5%;车辆行驶车速为90 km/h，空载、半载和满载状态下，系统检测误差分别为3.12%，7.616%和6.75%。该系统满足实际的需要，可以为物联网中车辆载荷实时远程监测提供技术支持。

［1］Niedzwiecki M，Wasilewski A.Application of adaptive filtering to dynamic weighing of vehicles［J］.Control Engineering Practice，1996 ，4(5):635-644.

［2］郭兰英.汽车动态称重系统算法研究［D］.西安:长安大学，2010.06.

［3］Zhou Z F，Cai P，Chen R X.Empirical mode decomposition in weigh-in-motion of vehicles［J］.Proceedings of the international conference on sensing，computing and automation，2006，Part4:1788-1791.

［4］陈广华，鞠 娜，杨 飞，等.基于粘贴式应变传感器的车辆超载监测系统［J］.北京航空航天大学学报，2011，37(4):409-414.

CHEN Guang-hua，JU Na，YANG Fei，et al. Monitoring system for vehicle overloading base on paste-type strain sensor［J］.Journal of Beijing university of Aeronautics and Astronautics，2011，37(4):409-414.

［5］苏 建.一种高精度带过载保护的汽车超偏载检测装置［P］.中国，发明专利，专利号:CN102173286A.

［6］陈杰平，陈无畏，祝 辉，等.基于Matlab/Simulink的随机路面建模与不平度仿真［J］.农业机械学报，2010，41(3):11-15.

CHEN Jie-ping，CHEN Wu-wei，Zhu Hui，et al.Modeling and simulation on stochastic road surface irregularity based on matlab/Simulink［J］.Transactions of the Chinese Society for Agricultural Machinery，2010，41(3):11-15.

［7］王直民，张土乔，吴小刚.不平整路面上的车辆等效动载系数［J］.浙江大学学报 (工学版)，2007，41(6):1007-1011.

WANG Zhi-min， ZHANG Tu-qiao， WU Xiao-gang.Equivalentvehicle dynamic load coefficienton rough pavement［J］.Journal of Zhejiang University(Engineering Science)，2007，41(6):1007-1011.

［8］李国勇.智能控制及其MATLAB实现［M］.北京:电子工业出版社，2005.

［9］周志峰.应变式汽车轴重动态测量系统性能增长研究［D］.上海:上海交通大学电子信息与电气工程学院，2007.11.

［10］ Zhou，Z F，Cai P.Estimating the axle load of vehicle in motion based on nonlinear curve-fitting ［J］.IET Science，Measurement＆ Technology，2007，1(4):185-190.

［11］ Norden E，Huang M L，Wu C，et al.A confidence limit for the empiricalmode decomposition and Hilbertspectral analysis［J］.Proceedings of the royal society of london series a-mathematical physical and engineering sciences，2003，2037(459):2317-2345.

［12］ www.ens-lyon.fr/～ flandrin/software.html.

［13］ Rilling G，Flandrin P，Goncalves P.On empirical mode decomposition and its algorithms.［C］.IEEE-EURASIP workshop on nonlinear signal and image processing NSIP-03，Grado(I)，2003.

［14］Li S W，Tian J J，Kui H L，et al.Design and implementation of vehicle monitoring and early-warning system based on wince［J］.Proceeding of international conference on electric information and control engineering，2011(8):2073-2076.