非线性结构动力学系统的首次穿越

任丽梅，徐 伟，李战国

(西北工业大学理学院，陕西西安 710072)

在地震工程，桥梁工程等领域中动力学系统的结构可靠性一直是研究的热点，而受到诸如地震、风及海浪等随机激励的动力学系统的首次穿越失效更是研究的焦点之一。首次穿越失效概率(简称:首穿失效概率)是结构安全性的重要指标，是指在某个时间段内结构响应首次超过指定安全域边界的概率。尽管这个问题已经得到了高度重视，但仍是结构安全性分析最具挑战性的问题，因为直到现在，即使是最简单的线性振子场合也无可利用的精确解。

自Rice［1-2］的开拓性研究以来，研究者虽然提出了基于Fokker-Planck方程的路径积分法、胞映射法、有限元等数值解法［3-5］，但这些方法的复杂度随状态空间维数的增加呈指数增加趋势，因此普遍认为等效线性化与基于方差缩减技巧的蒙特卡罗模拟方法是解决此类问题的选择［6］，研究者据此先后提出重要抽样法，受控蒙特卡罗法［7］，子集模拟法［8］，区域分解法［9］等，在方差缩减技巧中基于Gisranov定理的重要抽样法［10-15］已经被广泛应用。

基于Gisranov定理的重要抽样法可以描述为一种控制样本路径的方法:样本被集中在样本空间中最重要的部分，而不是均匀分布在样本空间中。然而达到这样的目的选择怎样的控制函数才是最关键的。在许多的研究中均是利用设计点来构造控制函数的，但仅在稳态高斯白噪声激励的线性系统场合，设计点具有解析表达式，在非线性系统场合，设计点的得到通常采用近似方法［16-18］。可是设计点的准确性直接影响到控制函数的控制功能，因此本文利用线性系统具有解析的设计点这一特性，首先根据Rice公式，得到与非线性系统方程具有相同平均上穿率的等效线性化系统方程，利用此等效线性化方程得到设计点的解析表达式，构造控制函数。然后将控制函数运用到非线性系统方程中。利用重要样本法估计非线性系统的首穿失效概率。最后文章以Duffing振子为例，模拟结果显示了方法的正确性与有效性。

1 重要样本法

设结构动力学系统响应是一p维向量X(t)=［X1(t)，X2(t)，…，Xp(t)］T且满足 Ito^随机微分方程:

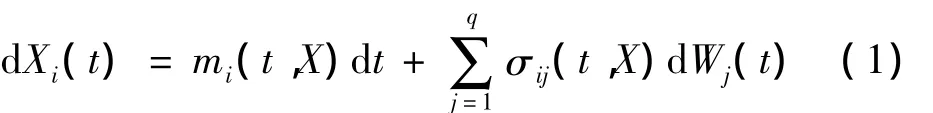
Xi(0)=xi，其中W(t)=［W1(t)，W2(t)，…，Wq(t)］T是具有概率测度p的标准Wiener过程。m(t，X)，σ(t，X)是漂移、扩散系数，分别满足李普希兹条件和增长性条件［19］。定义系统的安全域是D∈Rp。

首穿失效概率为

其中I［g(X)］是示性函数，

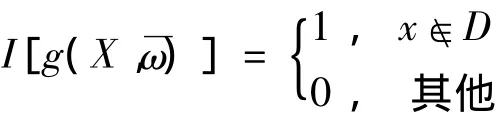
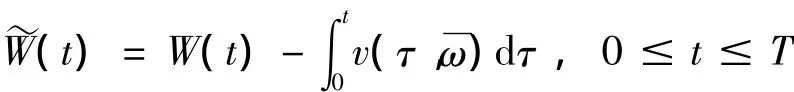
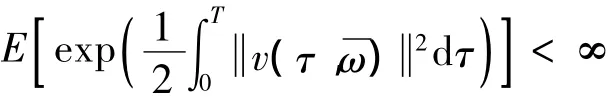
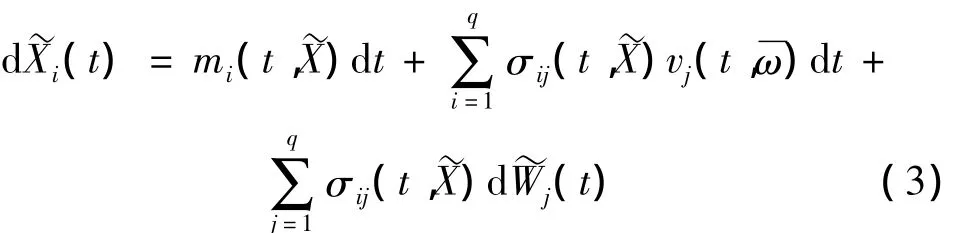
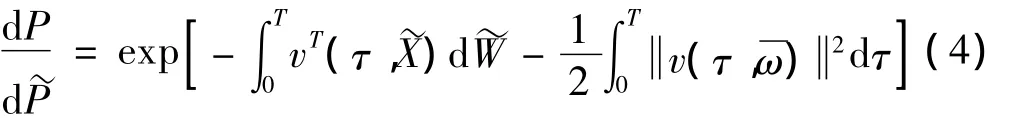
则在确定的初始条件下，基于概率测度 ~P的首穿失效概率的估计为

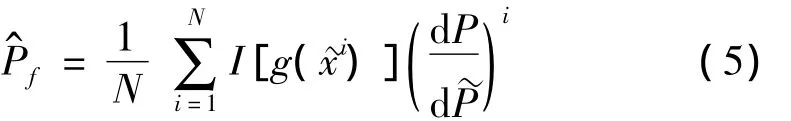
2 等效线性化

考虑零均值，具有单边谱密度G0的稳态高斯白噪声激励的Duffing振子:

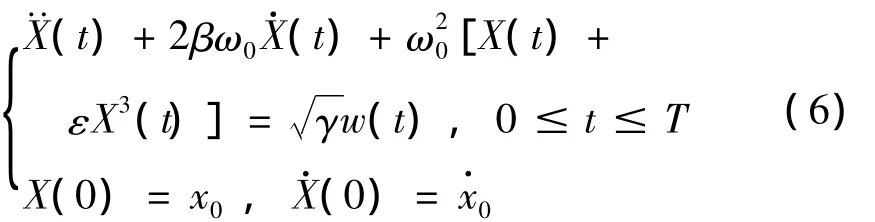
(x(t)(t))的稳态概率密度函数为

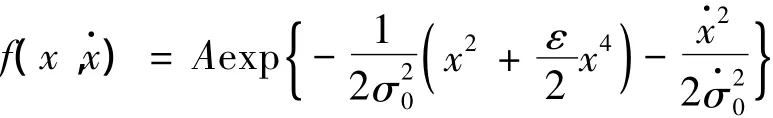
根据Poisson假设，利用Rica公式［19］，非线性方程的平均上穿率为:

即:

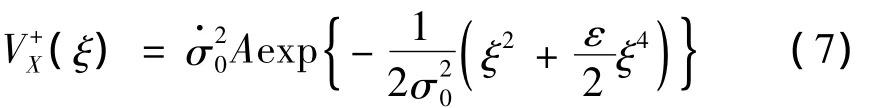
等效线性方程设为:

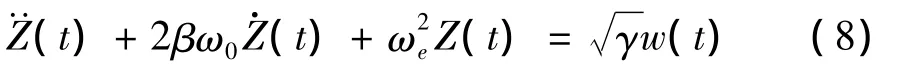
平均上穿率为:

其中:

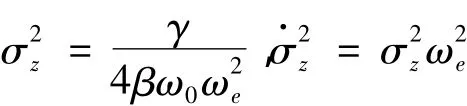
则解方程:

可得关于安全域边界b的等效线性化参数ωe值。当非线性系统的平均上穿率无法得到解析表达式时，可以利用数值方法。蒙特卡罗方法也可以用来估计平均上穿率，在稳态过程场合平均上穿率被定义为:

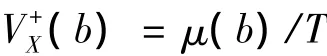
其中:μ(b)表示在时间间隔T内，稳态过程越出安全域的平均次数。

3 控制函数的构造

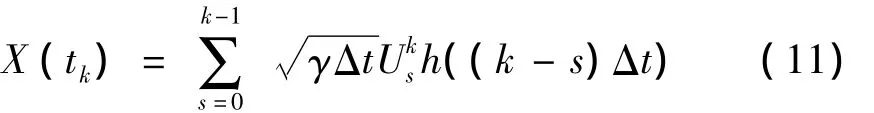
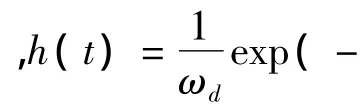
在tk时刻，极限状态方程为:

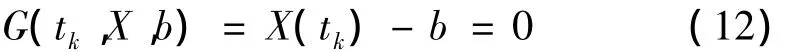
可靠性指标:

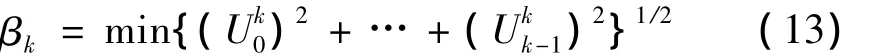
可得设计点为:

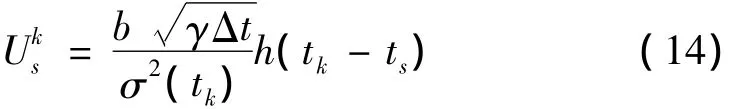
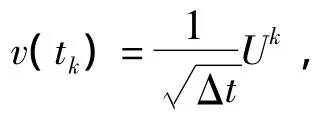
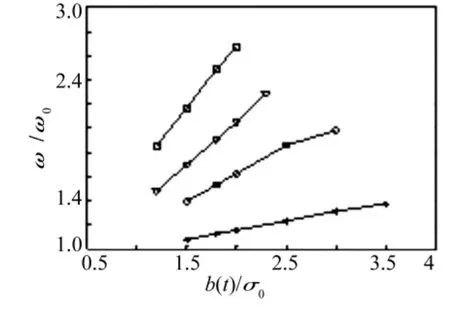
图1 等效线性化参数与安全域边界Fig.1 The frequencyvs threshold depending on different values of the non-linearity parameter ε.ε =0.1(*)ε=0.5(○)，ε=1(△)，ε=2(◇)

4 结果与讨论

振子方程如式(6)所示，可令X1(t)=X(t)，X2(t)=(t)，其Duffing振子的It o^随机微分方程为:

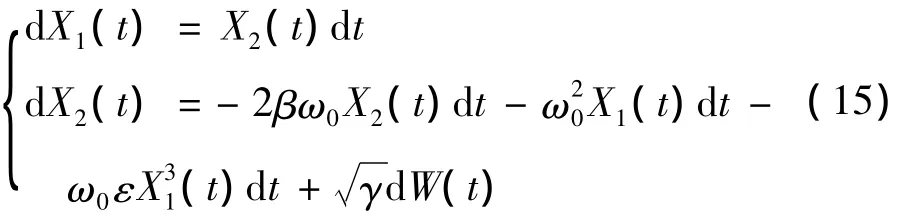
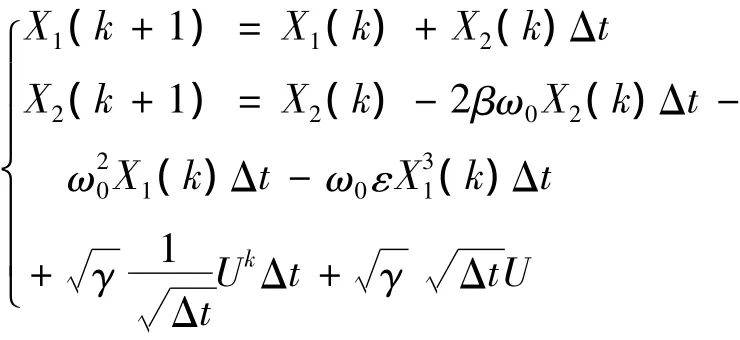
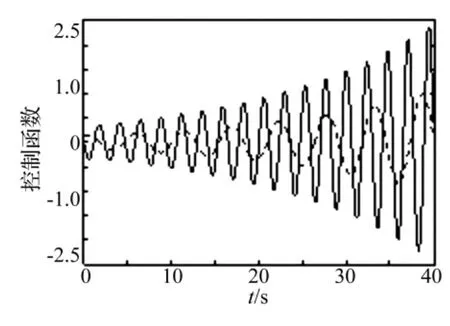
图2 控制函数图。ε=0.1虚线，ε=2实线Fig.2 Control function for an up-crossing of level b(t)=2.449 40 at time T=40 s.ε =0.1(dotted line)，ε=2(solid line)

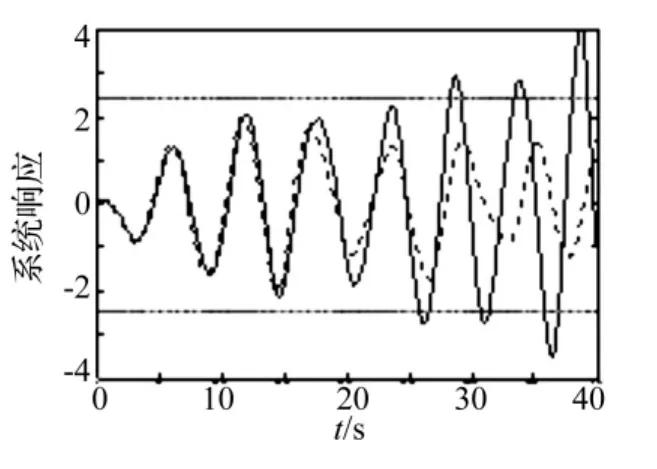
图3 加控制(实线)与不加控制(虚线)的系统(ε=0.1)响应比较图:Fig.3 The response of the non-linear system(ε =0.1)comparison chart:Add control(solid line)and not controlled(dotted line)

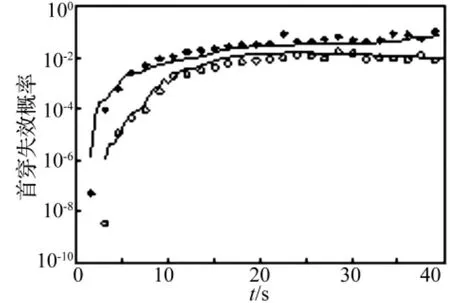
图4 失效概率图，b(t)=2.449 40，ε=0.01(* 线)，ε=2(○线)，原始蒙特卡罗法(实线)Fig.4 The first failure probability simulation comparison chart importance sampling procedure(ε =0.01(*)，ε=2(○))，crude Monte Carlo(solid line)

在稳态高斯白噪声激励的Duffing振子中，令β=0.05，ω0=1.0(rad/s)，γ =0.3，T=40 s，Δt=0.05，n=800，安全域边界取常数边界b(t)=kσ0。图1是当非线性参数分别为 ε =0.1，ε =0.5，ε =1，ε =2 时，不同安全域边界下等效线性化参数ωe与ω0的比值的示意图。图2是当ε=0.1(虚线)，ε=2(实线)的控制函数图。图3是当ε=0.1时Duffing振子加控制(实线)与不加控制(虚线)的系统相应比较图。从图3中可看出在20 s之前加控制与不加控制的系统响应大致相同，20 s之后控制函数力量强劲，起到了支配的作用，与振子达到共振频率，使得振子在26 s时首次越过安全域边界b(t)=2σ0=2.449 40。图4是在安全域边界为b(t)=2σ0时，利用重要样本法 ε=0.01(* 线)，ε=2(○线)(N=103)时的首穿失效概率与原始蒙特卡罗(实线，N=106)法的比较图，显示了两者很好的吻合，说明本文所提方法的正确性与有效性。

5 结论

本文基于Gisranov定理，提出了非线性结构动力系统首穿失效概率的重要抽样法。本文利用线性系统具有解析的设计点这一特性，根据Rice公式，得到非线性系统的等效线性化方程，等效线性化原理采用平均上穿率而非mean square原理，研究者A.Naess也在研究首次穿越失效问题中采用了此线性化原理，他也认为此线性化原理对研究首穿问题是更加合理的。利用等效线性化方程得到解析的设计点，构造控制函数。然后将控制函数运用到非线性系统方程中，非线性系统不同非线性化参数ε下进行了模拟，结果说明了方法的正确性与有效性，且本文方法所需样本量及计算时间远少于蒙特卡罗模拟。

［1］ Rice O C.Mathematical analysis of random noise［J］.Bell Syst Tech J，1944(23):282-332.

［2］ Rice O C.Mathematical analysis of random noise［J］.Bell Syst Tech J，1945(24):46-156.

［3］ Spencer B F，Bergman L A.On the numerical Solution of the Fokker-Planck equation for nonlinear stochastic systems［J］.Nonlinear Dynamic，1993(4):357-372.

［4］Li W，Xu W.Stochastic optimal control of first passage failure for coupled Duffing-Van derPol system under Gaussian white noise excitations ［J］.Chaos.Solitons＆ Fractal，2005，25(5):1221-1228.

［5］Li W，Xu W.First passage problem for strong nonlinear stochastic dynamical system［J］.Chaos.Solitons ＆ Fractal，2006，28(2):414-421.

［6］Proppe C，Pradlwarter H J，Schueller G I.Equivalent linearization and Monte Carlo simulation in Stochastic dynamics［J］.Probab Eng Mech，2003，18(3):1-15.

［7］ Pradlwarter H J，Schueller G I.Assessment of low probability events of dynamical systems by controlled Monte Carlo simulation［J］.Probab Eng Mech，1999，14(3):213-227.

［8］ Zuev K M，Katafygiotis L S.The Horseracing Simulation algorithm for evaluation of small failure probabilities［J］.Probab Eng Mech ，2011，26(2):157-164.

［9］Katafygiotis L，Cheung S H.Domain decomposrtion method for calculating the failure probability of linear dynamic systems subjected toGaussian stochasticloads［J］.Journalof Engineering Mechanics，2006，20:475-486.

［10］ Olsen A I，Naess A.An importance sampling procedure for estimating failure probabilities of Non-linear dynamic systems subjected to random noise［J］.J Non-linear Mech，2007(42):848-863.

［11］ Juu O，Hiroaki T.Importance sampling for stochastic systems under stationary noise having a specified power spectrum［J］.Probab.Eng.Mech.，2009，24(4):537-544.

［12］ Au S K，Beck J L.First excursion probability for linear systems by very efficient importance Sampling［J］.Probab.Eng.Mech.，2001，16(3):193-207.

［13］ Macke M，Bucher C.Importance sampling for randomly excited dynamical systems［J］.J.Sound Vibration.2003，268:269-290.

［14］ Olsen A I，Naess A.An importance sampling procedure for estimating failure probabilities of dynamic systems［C］//ASCE，Joint Speciality Conference on Probabilistic Mechanics and Structural Reliability，2004.

［15］ Pradlwarter H J，Schueller G I.Excursion probabilities of non-linear systems［J］.Int.J.Non Linear Mechanics，2004，39:1447-1452.

［16］ Der Kiureghian A.The geometry of random vibrations and solutions by FORM and SORM［J］.Probab.Engng.Mech.，2000，15(2):81-90.

［17］ Liu P L，Der Kiureghian A.Optimization algorithms for structural reliability［J］.Structural Safety，1991，9(3):161-177.

［18］ Zhang Y，Der Kiureghian A.Two improved algorithms for reliability analysis［C］//Rackwitz et al，editor.Proceedings of the 6thIfIP WG 7.5 conference on optimization of structural systems，1994:297-304.

［19］ Soong T T，Grigoriu M.Random vibration of mechancial and structural systems［M］.Prentice-Hall.Inc.Englewood Cliffs，NJ，1997.