拉压刚度不同桁架的动力参变量变分原理和保辛算法

高 强，张洪武，张 亮，钟万勰

(大连理工大学 工程力学系，工业装备结构分析国家重点实验室，大连 116024)

经典弹性理论描述的是拉压弹性模量相同材料的力学问题，但实际工程中由于不同的功能需求，从而对结构形式或构成这些结构的材料有不同要求。譬如，工程中常用的混凝土材料，表现出拉、压性质不同的特点;而对于一些展开结构，为达到其设计性能，必须采用特殊的索、膜结构，这些索、膜部件同样表现出不同的拉压性质。具有拉、压不同性质的材料或结构的力学分析，体现出较强的非线性特征，需要针对这类问题发展有效的求解算法。

拉、压模量不同问题的理论研究始于上个世纪40年代。Timoshenko［1］提出了双模量的概念。Ambartsumyan［2］研究了拉、压模量不同圆柱壳的轴对称性问题，并依据主应力的正负，给出了此类问题在主方向上的本构关系。Ambartsumyan［3］总结分析了大量新型材料的试验数据，将拉、压不同模量材料的本构关系总结为双直线模型，并且详细论述了弹性系数的选取。拉压不同模量问题的研究有着广泛的应用背景，张拉整体结构是典型的含有不同拉压刚度的结构。文献［4］推导了张拉整体结构平衡构型附近的线性化动力学模型。文献［5］研究了张拉整体结构的动力学行为和控制策略。文献［6］对张拉整体结构的动力学特点、求解方法和存在的问题作了综述。

在数值求解方面，国内学者进行了大量的相关研究。张允真等［7］构造了双模量问题求解的有限元格式，进行迭代求解。杨海天等［8］提出了用初应力法迭代求解双模量弹性问题。刘相斌等［9］进一步讨论了双模量问题的剪切模量，提出了加速收敛因子的思想。He等［10］详细讨论了传统迭代求解方法的收敛问题。杨海天等［11］讨论了拉压双模量问题的动力分析问题。叶志明等［12］简述了不同模量弹性问题理论及其有限元法的研究与发展。杨海天等［13］利用光滑函数技术，提出光滑化的拉压不同弹性模量问题的应力应变关系，与有限元方法相结合，建立了拉压不同模量一维连续体与桁架结构的数值求解模型。对于这类结构的特殊非线性问题，如何保证算法的稳定性是数值模拟的主要问题之一。

根据结构力学与最优控制的模拟关系，钟万勰等［14-15］建立和发展了参变量变分原理和基于此变分原理的一系列数值算法，已成功应用于弹塑性［14-15］、接触［16-18］、摩擦［17-18］和纳米管范德华力模拟［19］等非线性问题分析。本文在参变量变分原理基础上，建立了由拉压刚度不同杆单元组成的桁架结构的动力学参变量变分原理。将拉压刚度不同桁架问题的非线性动力分析转换为线性互补问题求解。结合时间有限元方法构造了求解此问题的保辛数值积分方法。此方法不需要刚度矩阵更新和迭代，计算过程高效、稳定性好。

1 拉压不同刚度杆单元的动力参变量变分原理

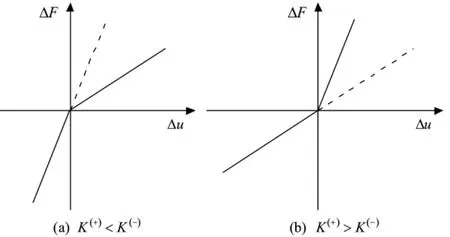
图1 拉压刚度不同杆的本构关系Fig.1 The constitutive relation for rod with different module in tension and compression

考虑具有不同拉压刚度的杆，设拉伸和压缩刚度分别为K(+)和K(-)，K(+)≠K(-)，可分为两种情况，如图1。在图1(b)中，如果压缩模量等于零，则成为绳索。杆的本构关系为:

其中:

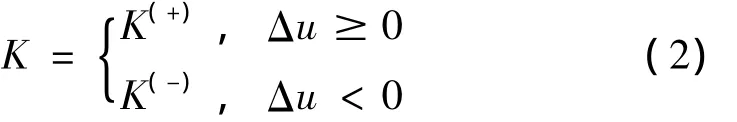
首先假设K(+)＜K(-)，即图1(a)所示情况。将本构关系写为如下的统一形式:

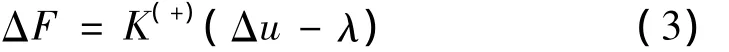
则要求:

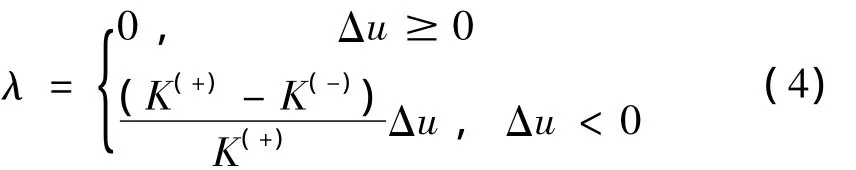
上式与如下的互补关系等价，即:

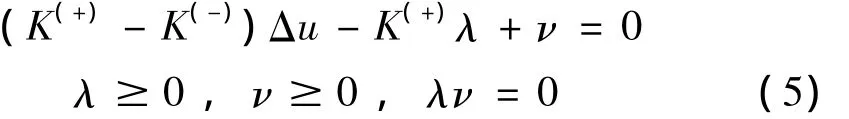
则杆的势能为:

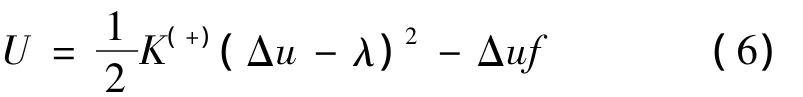
因此，当K(-)＞K(+)时，杆的参变量变分原理为:

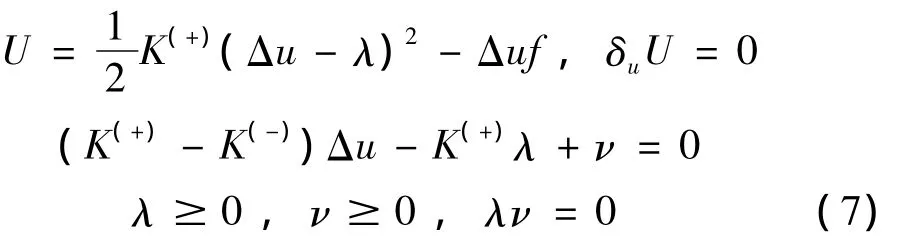
其中:下标u表示只对Δu进行变分，而λ作为参变量不变分。同理，如果K(-)＜K(+)，可类似写出参变量变分原理为:

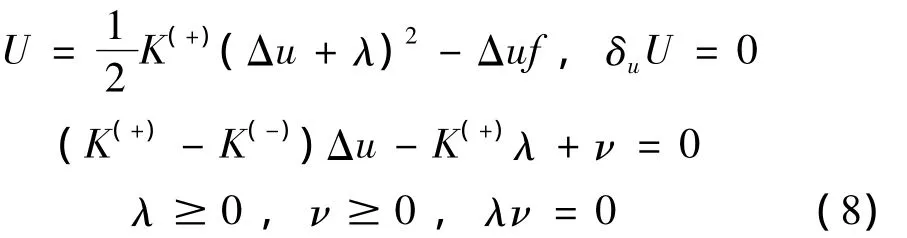
当然，也可将本构关系写为如下的形式，即:

则当K(-)＞K(+)时，参变量变分原理为:

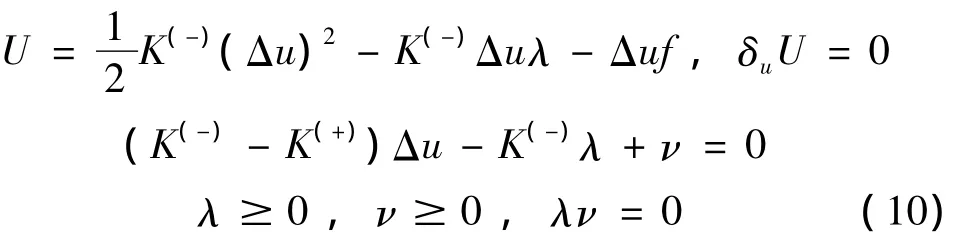
而当K(-)＜K(+)时，参变量变分原理为:

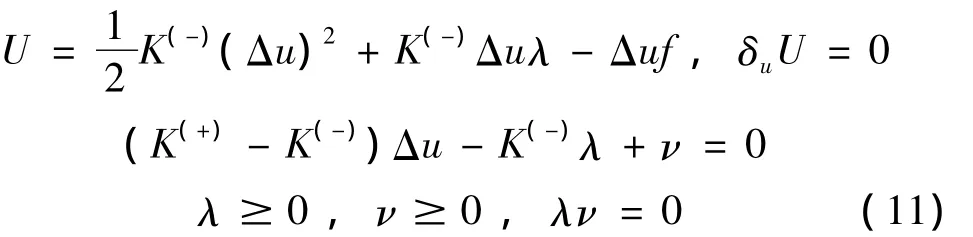
方程(7)，(8)，(10)和(11)描述的四种参变量变分原理可统一写为:

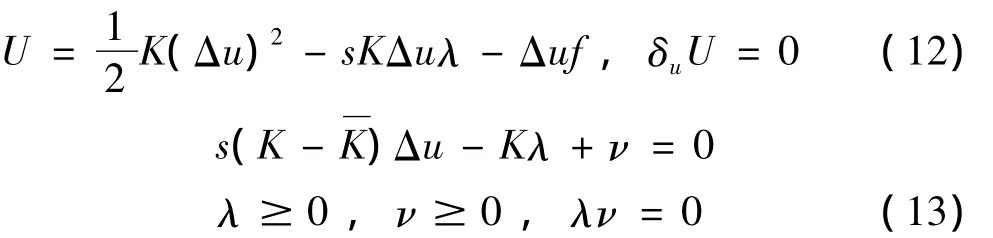
符号sign表示取符号，其定义为:

容易证明方程(12)和(13)给出的参变量变分原理与方程(1)和(2)给出的平衡方程等价，具体的证明过程见文献［9-10］。

以上给出的是单根杆的参变量变分原理，将杆组合成桁架时，涉及到局部坐标和整体坐标之间的转换，局部坐标和整体坐标之间的关系如图2所示。

图2 坐标转换Fig.2 The coordinate transformation

在局部坐标下有:

局部坐标与整体坐标下的位移之间的关系为:

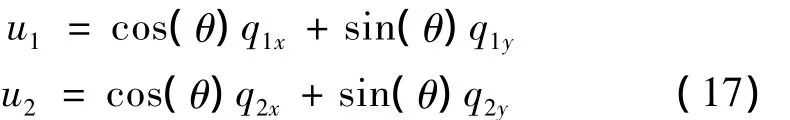
其中:

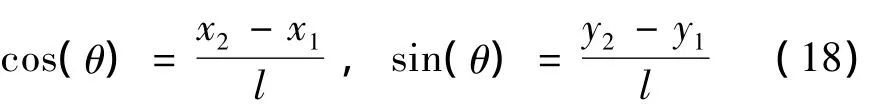
因此有:

其中:

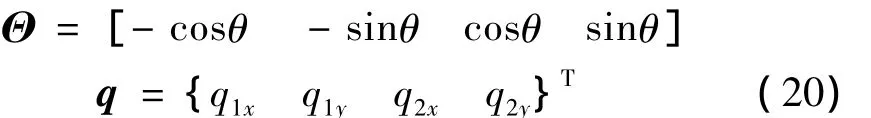
对于空间结构，转换关系依然是方程(19)，只是:

其中:

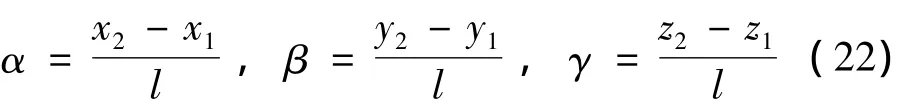
给出位移在局部坐标和整体坐标之间的关系后，既可在总体坐标下，将桁架所有的杆单元按照有限元的方式进行集合，则得到整个桁架结构的参变量变分原理为:

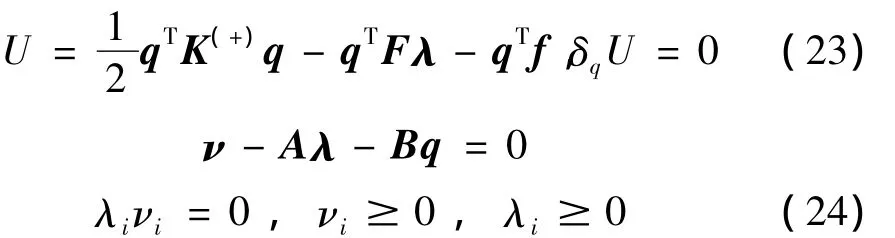
其中:

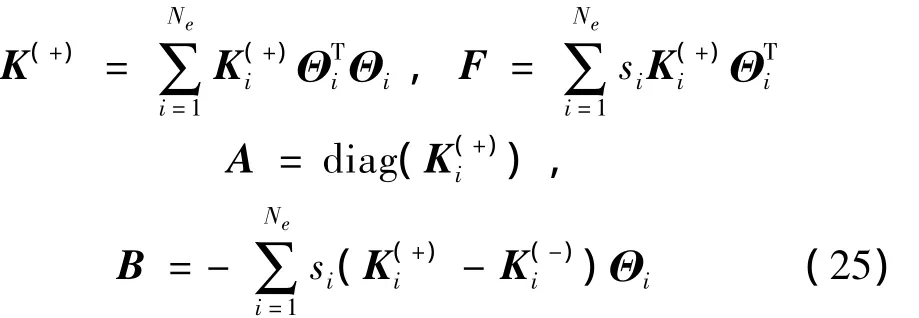
其中Ne表示杆单元的数量。

下面考虑动力学问题，本文考虑的是无阻尼系统，因此动力学方程可通过Euler-Lagrange方程给出。Lagrange函数L的定义为:

其中T和U分别表示动能和势能。上文已经给出了不同拉压刚度杆的势能U，而动能T为:

其中M是质量矩阵。因此有:

则动力学方程可由Hamilton变分原理给出，即:

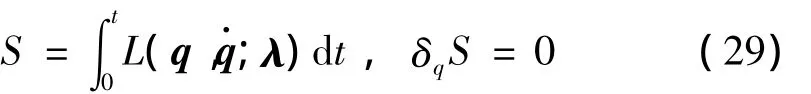
变分后可给出动力学运动方程为:

当然，动力学方程还受互补条件约束，即方程(24)。

2 保辛方法

动力系统积分时，选取一个时间步长η，于是得到一系列等步长的时刻

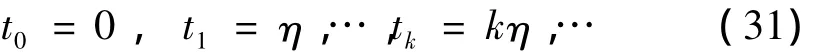
在一个典型的积分步长t∈［tk-1，tk］内，将位移q(t)、参变量λ(t)和外力f(t)用线性函数近似，即:

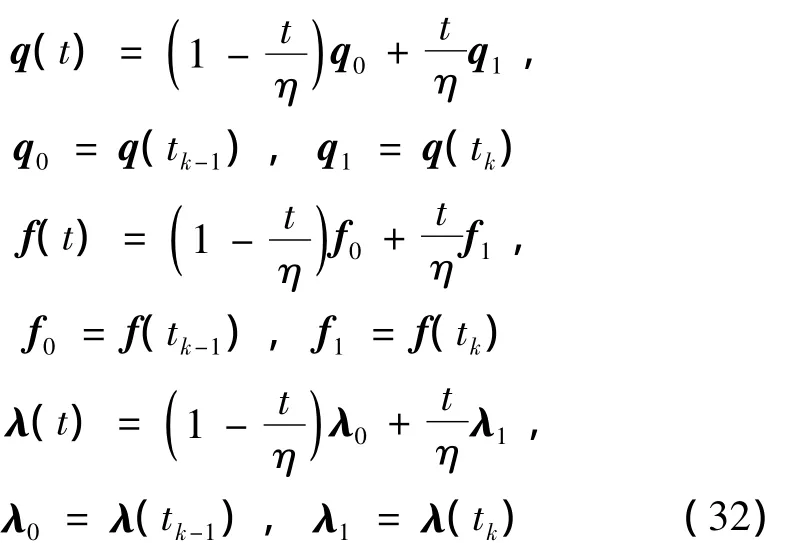
将它们代入方程(29)中的作用量S，并积分得到近似作用量为:

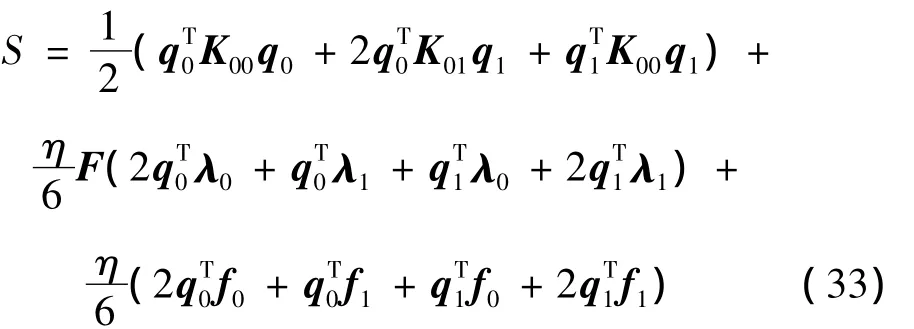
其中:

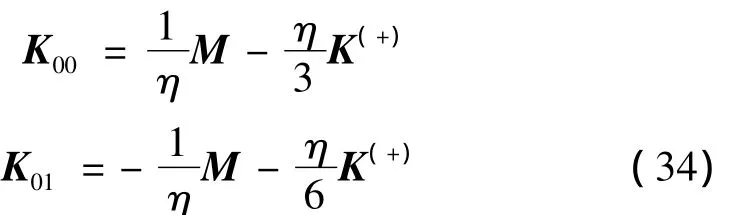
根据离散Hamilton正则方程:

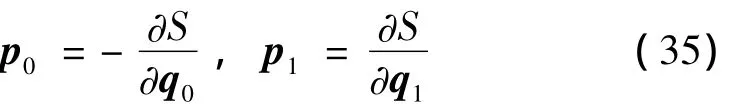
并通过方程(35)可得到:

其中:

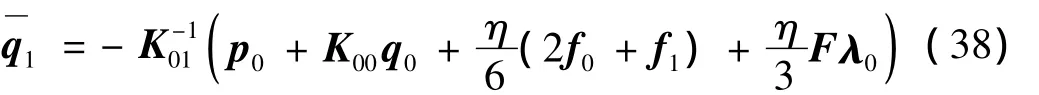
将方程(36)带入互补条件(24)得到:

求解线性互补问题(39)，可求得λ1，然后根据方程(36)和(37)可计算出q1和p1，从而完成一个时间步的积分。

3 数值算例

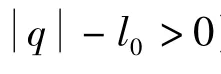
图3 含有绳单元的单质点结构Fig.3 One DOF system with string elements

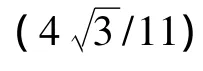
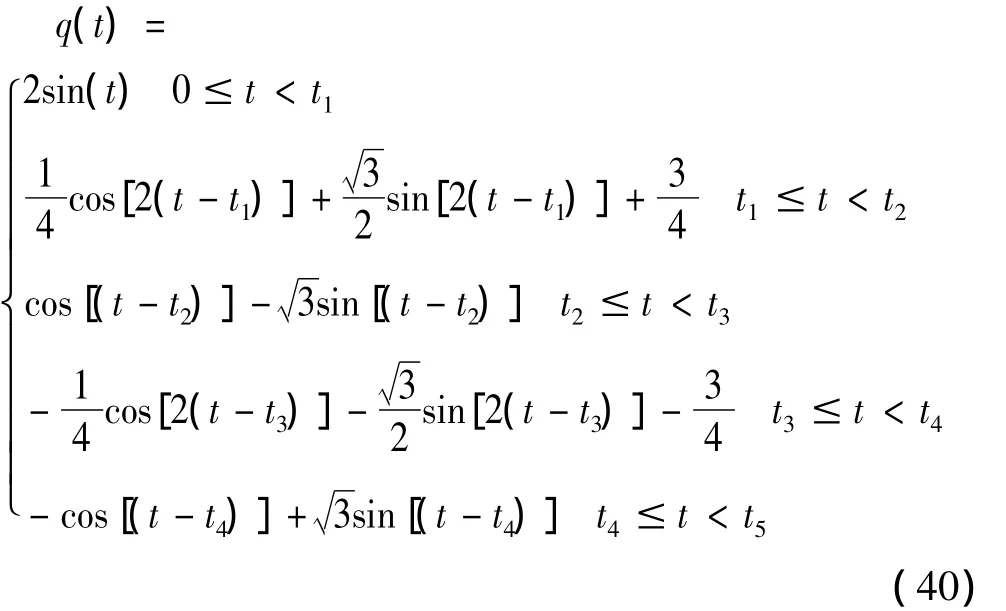
其中:

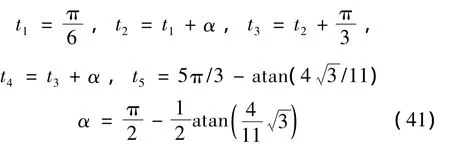
采用时间步长η=0.1 s积分到100 s，得到的位移和动量如图4，其中实线表示本文方法计算结果，圆圈表示解析解，可以看到本文方法积分得到的结果与解析解非常吻合，证明了本文方法的正确性。若在质点上施加外载荷f(t)=sin(t)N，其它参数同上，则积分得到的位移和动量如图5。

图4 自由振动质点的位移和动量Fig.4 The displacement and momentum responses for free vibration

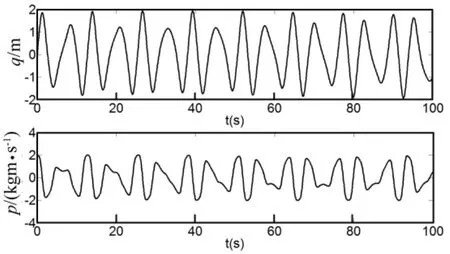
图5 强迫振动质点的位移和动量Fig.5 The displacement and momentum responses for forced vibration

算例2:考虑如图6所示的桁架结构，图中实线表示拉压模量相同的杆，它们具有相同的杨式模量和密度，分别为E=105N/m2和ρ=3×103kg/m3。虚线表示绳，即具有拉伸模量，而受压时模量为0，左右两根斜的绳具有相同拉伸模量E=2×105N/m2，中间的竖绳拉伸模量E=105N/m2，所有绳的质量忽略，所有杆和绳的面积为A=10-3m2。

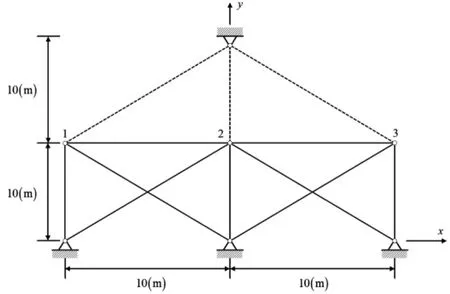
图6 具有绳索单元的桁架结构Fig.6 The truss structure with string elements

考虑结构的自由振动，取所有节点初始位移为0，而初始动量为:节点1水平动量为1，竖直动量为0，节点2水平动量为0，竖直动量为1，节点3水平动量为-1，竖直动量为0。采用步长η=0.2(s)积分到400 s，得到的各节点位移和动量响应如图7，其中图7(a)和(b)分别给出了3个节点x和y方向的位移，图7(c)和(d)分别给出了3个节点x和y方向的动量。由于结构的对称性和初始条件的对称性，其响应也具有对称性，而计算结果很好的体现了这种对称性。3条绳索的参变量变化如图8，参变量不等于零表示绳索处于松弛状态。

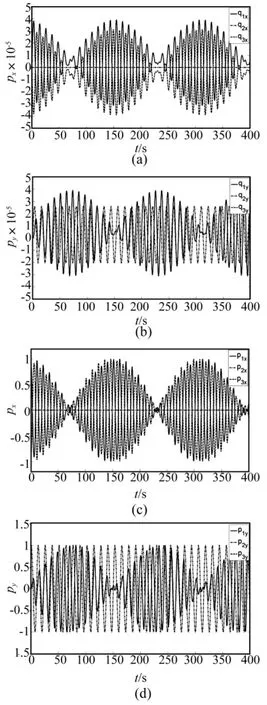
图7 平面桁架的响应Fig.7 The responses of the truss structure

采用步长η=0.2(s)积分到1 000 s，得到的系统能量的相对误差分别如图9。图9表明本文方法给出的积分方法不会引入人工阻尼，能量始终在一定范围内变化，这是保辛方法的典型特征。

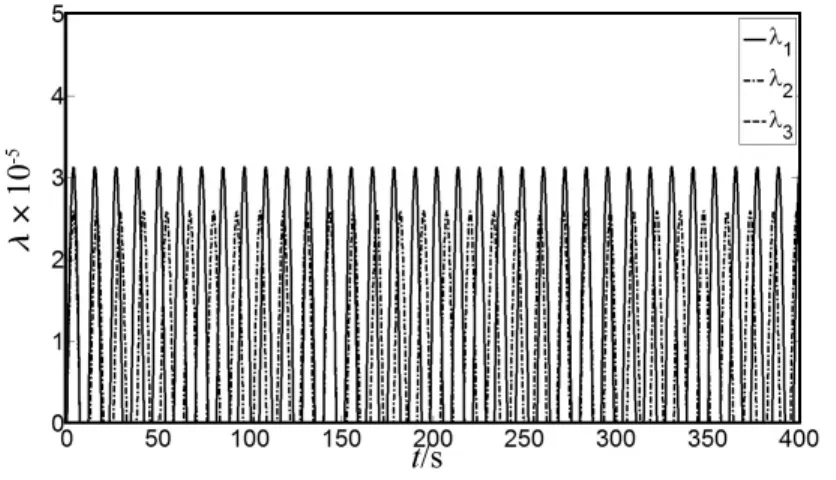
图8 参变量随时间变化Fig.8 The parametric variables

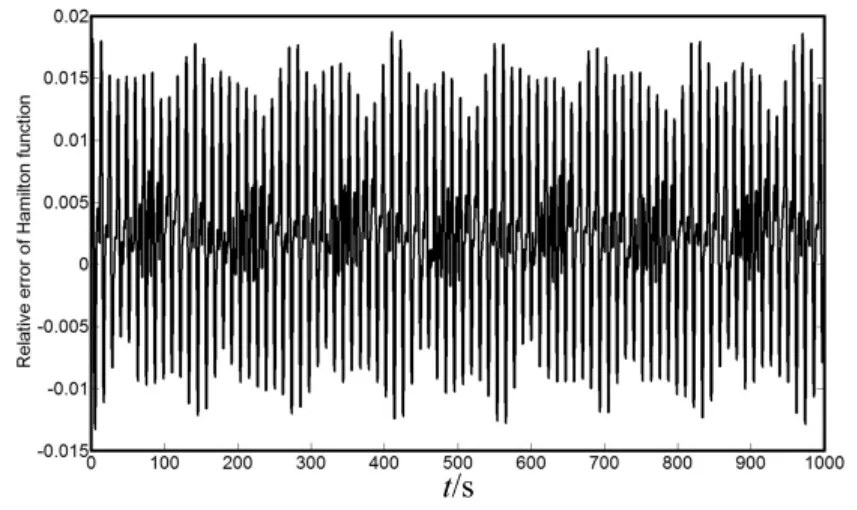
图9 能量的相对误差Fig.9 The relative error of the Hamiltonian function

4 结论

本文建立了由拉、压刚度不同杆单元组成的桁架结构的动力学参变量变分原理，将拉、压刚度不同桁架问题的非线性动力分析转换为线性互补问题求解。结合时间有限元方法构造的保辛数值积分方法，在时间步内不需要迭代和刚度矩阵更新，可精确、高效的求解此类问题，且计算过程稳定。该方法也可自然推广到3-D桁架结构。

［1］ Timoshenko S.Strength of Materials，part II:Advanced theoryand problems ［M］. 2nded. Princeton:Van Nostrand，1941.

［2］Ambartsumyan S A.The Axisymmetric problem of circular cylindrical shell made of materials with different stiffness in tension and compression［J］. AkademiiNauk SSSR，Mekhanika，1965(4):77-85.

［3］Ambartsumyan S A著，张允真译.不同模量弹性理论［M］.北京:中国铁道出版社，1986.

［4］ Cornel S，Martin C，Robert E S.Linear dynamics of tensegrity structures［J］.Engineering Structures，2002，24:671-685.

［5］ Bel H A N，Smith I F C.Dynamic behavior and vibration control of a tensegrity structure［J］.International Journal of Solids and Structures，2010，47:1285-1296.

［6］ Mirats T，Hernandez J.Tensegrity Frameworks:Dynamic analysis review and open problems［J］.Mechanism and Machine Theory，2009，44:1-18.

［7］张允真，王志峰.不同拉压模量弹性力学问题的有限元法［J］.计算结构力学及其应用，1989，6(1):236-254.

ZHANG Yun-zhen， WANG Zhi-feng.The finite element method for elasticity with different moduli in tension and compression［J］.Computational Structural Mechanics and Applications，1989，6(1):236-254.

［8］杨海天，邬瑞锋，杨克俭，等.初应力法解拉压双弹性模量问题［J］.大连理工大学学报，1992，32(1):35-39.

YANG Hai-tian， WU Rui-feng， YANG Ke-jian， et al.Solution to problem of dual extension-compression elastic modulus with initial stress method［J］.Journal of Dalian University of Technology，1992，32(1):35-39.

［9］刘相斌，张允真.拉压不同模量有限元法剪切弹性模量及加速收敛［J］.大连理工大学学报，1994，34(6):641-645.

LIU Xiang-bin，ZHANG Yun-zhen.Modulus of elasticity in shear and accelerate convergence ofdifferentextension compression elastic modulus finite element method ［J］.Journal of Dalian University of Technology，1994，34(6):641-645.

［10］ He X T，Zheng Z L，Sun J Y.Convergence analysis of a finite element method based on different moduli in tension and compression ［J］. InternationalJournalofSolids and Structures，2009，46:3734-3740.

［11］杨海天，杨克俭，张锡成，等.拉压双模量问题的动力分析［J］.计算结构力学及其应用，1993，10(4):438-448.

YANG Hai-tian，YANG Ke-jian，ZHANG Xi-cheng，et al.Dynamic analysis forthe problem ofdualextensioncompression elastic modulus［J］.Computational Structural Mechanics and Applications，1993，10(4):438-448.

［12］叶志明，陈 彤，姚文娟.不同模量弹性问题理论及有限元法研究进展［J］.力学与实践，2004，26(2):9-14.

YE Zhi-ming，CHEN Tong，YAO Wen-juan.Progress in elasticity theory with differentmoduliin tension and compression and related FEM［J］.Mechanics and Practice，2004，26(2):9-14.

［13］杨海天，张晓月，何宜谦.基于敏度分析的拉压不同模量桁架问题的数值分析［J］.计算力学学报，2011，28(2):237-242.

YANG Hai-tian，ZHANG Xiao-yue，HE Yi-qian.Sensitivity analysis based numerical solution for truss structures with bimodulus［J］.Journal of Computational Mechanics，2011，28(2):237-242.

［14］钟万勰，张洪武，吴承伟.参变量变分原理及其在工程中的应用［M］.北京:科学出版社，1997.

［15］张洪武.参变量变分原理与材料和结构力学分析［M］.北京:科学出版社，2009.

［16］ Zhang H W，Xu W L，Di S L，et al.Quadratic programming method in numerical simulation of metal forming process［J］.Computer Methods in Applied Mechanics and Engineering，2002，191:5555-5578.

［17］ Zhan H W，He S Y，Li X S，Wriggers P.A new algorithm for numerical solution of 3D elastoplastic contact problems with orthotropic friction law［J］.Computational Mechanics，2004，34:1-14.

［18］ Zhang H W，He S Y，Li X S.Two aggregate-function-based algorithms for analysis of 3D frictional contact by linear complementarity problem formulation［J］.Computer Methods in Applied Mechanics and Engineering， 2005， 194:5139-5158.

［19］ Zhang H W，Wang J B，Ye H F，et al.Parametric variational principle and quadratic programming method for van der Waals force simulation of parallel and cross nanotubes［J］.International Journal of Solids and Structures，2006，44:2783-2801.