基于有限元的斜齿轮设计分析❋
2013-09-04杨志帮
杨志帮
(开封大学 机械与汽车工程学院 ,河南 开封 475004)
0 引言
在机械传动系统中,齿轮传动是最主要的传动方式,齿轮的寿命关系着整个机构的寿命,而齿轮的寿命主要与齿面所受的接触应力和齿根的弯曲应力大小有关[1]。齿轮的承载能力主要受接触强度和弯曲强度的限制。在齿轮参数不变的情况下,给它增加载荷,就会发现齿轮弯曲应力的增加程度要比接触应力大得多。轮齿在受载时,齿根处产生的弯曲应力最大,再加上齿根过渡部分的截面突变及加工刀痕等引起的应力集中,都会致使轮齿折断[2]。因此本文利用有限元软件,分析出齿轮的应力分布情况,找出应力集中点,为齿形设计提供依据,并形成对齿轮分析的一整套方法,为新齿轮的设计提供理论依据。
1 斜齿轮有限元模型的建立
一般构造有限元模型的方法有直接建模、实体建模、输入实体模型[3]3种。在本文中使用CAXA实体造型中的斜齿轮菜单项,齿轮的各项齿形参数在此直接给出,然后对齿轮进行精确建模,最后使用“文件”菜单中的“数据接口”输出,将建立的模型文件保存成IGES格式,在ANSYS的接口下将模型导入其中。本文建立的斜齿轮实体模型如图1所示。
2 进行载荷计算与施加约束
齿轮在交变载荷的作用下,其轮齿容易发生折断,当齿根弯曲应力超过材料所允许的承受限度时,在齿根处就会产生一些微小的裂纹,随着载荷的继续作用,裂纹会不断扩展,这样就容易导致轮齿疲劳折断。
齿根弯曲疲劳强度的校核公式为:

其中:σF为实际计算出的最大弯曲应力;[σF]为设计齿轮的许用弯曲应力,[σF]=σFlim/SF,SF为弯曲疲劳强度安全系数(一般取值1.4~2),σFlim为试验齿轮弯曲疲劳极限应力,其值可查齿轮传动设计手册[4,5]。
2.1 斜齿轮分析参数
模型建立后,在ANSYS中定义该斜齿轮的材料属性。考虑到材料的性质,本模型中选取斜齿轮材料为20CrNi2Mo,经渗碳淬火,表面硬度为60HRC,各向同性,弹性模量E=210GPa,泊松比μ=0.3,密度ρ=7 850kg/m3。通过查询齿轮传动设计手册,文中材料的弯曲强度取为900MPa,安全系数SF取1.6,可计算出许用弯曲应力为:[σF]=900/1.6=562.5MPa。
2.2 对斜齿轮进行网格划分、设定约束条件和载荷
在ANSYS中,由于Solid45-8节点单元具有弹塑性、蠕变、扩张性、应力硬化、大变形和大应变等特性,因此本模型我们使用四面体实体单元Solid45-8。在自由网格划分时采用Mesh Tool命令,然后再对轮齿部分进行一定细化处理。本例中共生成单元数76 084,节点数23 210。斜齿轮网格划分的有限元模型如图2所示。
在此根据齿轮的运动特性,将齿轮内圆表面的所有节点加以固定约束,限制x、y、z三个方向上的自由度[6,7]。在条件约束完成后,我们把载荷加在啮合齿轮轮齿的齿顶线处。由于载荷F的大小与转矩T直接相关,在此先确定输入转矩T,此处假设齿轮的额定功率P=1.5MW,齿轮的转速n=356.9r/min,经计算转矩T=9.55(P/n)=40.14kN·m。转矩T求出后,可计算出F=2T/d=2T/mz=349kN(其中,d为齿轮分度圆直径,m为齿轮模数,z为齿数),最后再进行载荷F的加载,见图2中箭头所指部分。

图1 斜齿轮的实体模型
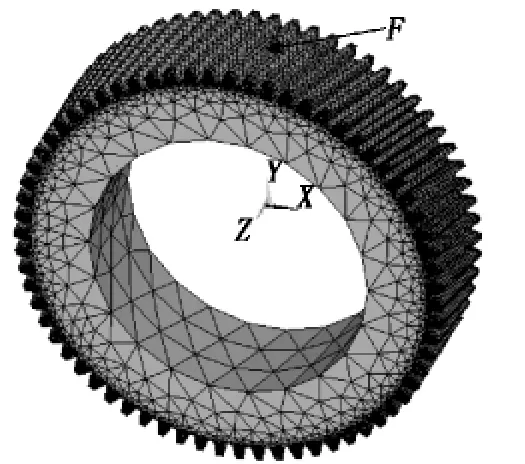
图2 斜齿轮的有限元模型
2.3 求解斜齿轮的齿根弯曲应力
加载完成后,在ANSYS中点击求解当前过程,我们选择stress/von Mises就可以生成齿轮的齿根等效弯曲应力云图,见图3。从分析结果中可知斜齿轮的最大von Mises应力为5.09×108Pa,即509MPa,该值小于材料的许用应力[σF]=562.5MPa,从而满足了该斜齿轮弯曲强度要求。由图3可以得出该斜齿轮的最大应力值出现在轮齿的齿根部分,见图3圈中。
3 结论
本文以斜齿轮为分析对象,利用有限元分析软件ANSYS对其进行齿根弯曲应力分析。首先选择单元类型与划分网格,然后建立了斜齿轮的有限元模型,最后经加载计算得出齿轮弯曲应力云图。分析结果显示了最大齿根弯曲应力的位置及值的大小。由此可以得出:①斜齿轮在外载荷的作用下,轮齿根部的弯曲应力最大,其变形越接近齿根越大,齿根部分变形最大;②在载荷的作用下,齿根过渡圆角处应力最大,最大弯曲应力值为509MPa。综述分析结果可知,齿轮弯曲破坏容易从齿根先出现。本文所采用的分析方法和分析结果也为其他齿轮的设计与计算提供了重要的参考依据。
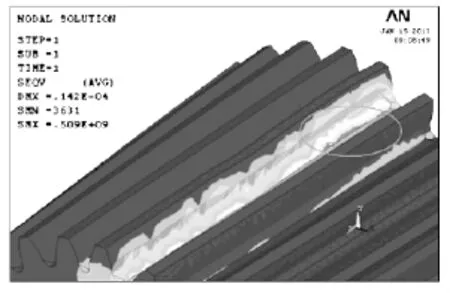
图3 斜齿轮的应力云图
[1] 徐步青,王立彬.齿轮模型应力的确定及有限元分析[J].石家庄铁道学院学报,2002(12):56-58.
[2] 杨生华,王统.齿轮轮齿变形中的接触有限元仿真分析[J].煤矿机械,1999(8):9-11.
[3] 李常义.基于ANSYS的渐开线圆柱齿轮参数化造型与有限元建模及分析技术[J].机械传动,2004,28(6):25-29.
[4] Lewis P E,Word W r.Finite element method principles and applications[M].New Jersey :Addision-Wesley,1991:200-204.
[5] 朱孝录.齿轮传动设计手册[M].北京:化学工业出版社,2005.
[6] 许艳.风力发电机组关键部件的有限元分析[D].乌鲁木齐:新疆大学,2005:46-47.
[7] 叶友东.基于ANSYS的渐开线直齿圆柱齿轮有限元分析[J].煤矿机械,2004,18(6):43-45.
